17.4: Trinquete de polimerización y trinquete de translocación

Los trinquetes de polimerización y translocación se refieren a procesos que dan como resultado desplazamientos direccionales de una cadena de polímero u oligómero r ather que una proteína específica. Los modelos para estos trinquetes también implican movimiento browniano rectificado, en el que una unidad de unión es un dded a una cadena difusora para sesgar el movimiento difusivo en una dirección deseada. Una vez que el desplazamiento alcanza una cierta longitud de difusión, un monómero o prot ein de unión puede agregarse a la cadena, bloqueando la difusión hacia adelante de la cadena. En este caso, es la unión o unión de unidades proteicas la que consume energía, típicamente en forma de ATP o r hidrólisis de GTP.

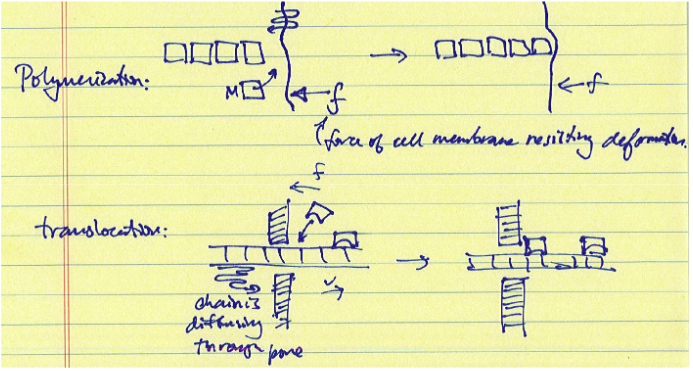
Trinquete Translocación ¹

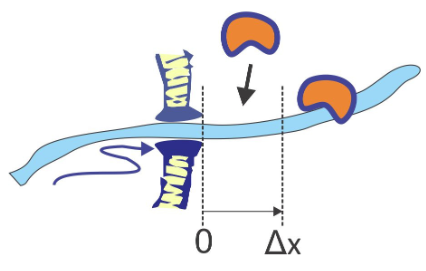La translocación de proteínas a través de las membranas ce ll es un proceso ubicuo para el transporte de cadenas polipeptídicas a través de membranas bacterianas y orgánulos a través de canales s con la ayuda de proteínas chaperonas en el lado interno de th e membrana. La translocación r atchet se refiere a un modelo en el que el transporte de la cadena se produce a través del movimiento browniano el cual es rectificado por la unión de proteínas a la cadena en un lado del poro a medida que se desplaza. Una vez que la cadena difunde s a través del poro por una distancia Δ x, una proteína puede unirse a la cadena, deteniendo la difusión hacia atrás. En cada paso, se requiere energía para impulsar la unión de la proteína chaperona.

El trinquete de translocación se refiere a un modelo continuo para la fusión d de la cadena. Es posible mapear este problema de difusión en una ecuación de Smoluchowski, pero sería difícil de resolver para la densidad de probabilidad. Es más fácil si solo estamos interesados en describir la velocidad promedio de la cadena en condiciones de estado estacionario, podemos resolver para el flujo de cadena en estado y en lugar a través del poro:

\[J(x) = -D \left( \dfrac{\partial P}{\partial x} + \dfrac{f}{k_BT}P \right) \]

where f is the force acting against the chain displacement. Steady state behavior corresponds to \( \partial P/\partial t =0 \) , so from the continuity equation

\[ \dfrac{\partial P}{\partial t} = -\dfrac{\partial J}{\partial x} \nonumber \]

we know that \(\partial J/\partial x = 0 \). Therefore J is a constant. To find P, we want to solve

\[ \dfrac{\partial P}{\partial x} + \dfrac{f}{k_BT}P+\dfrac{J}{D} = 0 \nonumber \]

for which the general solution is \(P=A_1e^{-fx/k_BT}+A_2\). We find the integration constants using the boundary condition \(P(\Delta x,t )=0 \), which reflects that a protein will immediately and irreversibly bind once the diffusing chain reaches an extension \(\Delta x\). (No back-stepping is allowed.) And we use the conservation statement:

\[ \int_0^{\Delta x} dx P(x) = 1 \nonumber \]

which says that a protein must be bound within the interval 0 to Δx. The steady-state probability distribution with these two boundary conditions is

\[ P(x) = \dfrac{ \underset{ \sim }{f} \left[ \exp \left( \underset{ \sim }{f} (1-x/\Delta x) \right) -1 \right] }{\Delta x\left( 1+ \underset{ \sim }{f} - e^{ \underset{ \sim }{f} } \right) } \]

\[ \underset{ \sim }{f} = \dfrac{f \Delta x}{k_BT} \nonumber \]

\( \underset{\sim}{f}\) is a dimensionless constant that expresses the load force in units of k_BT opposing ratchet displacement by Δx.

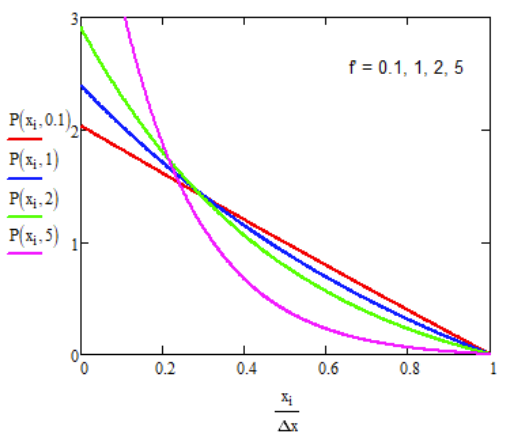
Substituting eq. (17.4.2) into eq. (17.4.1) allows us to solve for J.

\[J(x) =\dfrac{-D\underset{ \sim }{f}^2 }{\Delta x^2\left( 1+ \underset{ \sim }{f}-e^{\underset{ \sim }{f}} \right) } \left( 1-2\exp \left[ \underset{ \sim }{f} \left( \dfrac{x}{\Delta x} -1 \right) \right] \right) \nonumber \]

Now, the average velocity can be determined from \(\langle \nu \rangle = J\Delta x \). Evaluating the flux at x = Δx:

\[ \langle \nu \rangle =\dfrac{2D}{\Delta x} \left[ \dfrac{\underset{ \sim }{f}^2/2}{e^{\underset{ \sim }{f}}-\underset{ \sim }{f}-1} \right] \nonumber \]

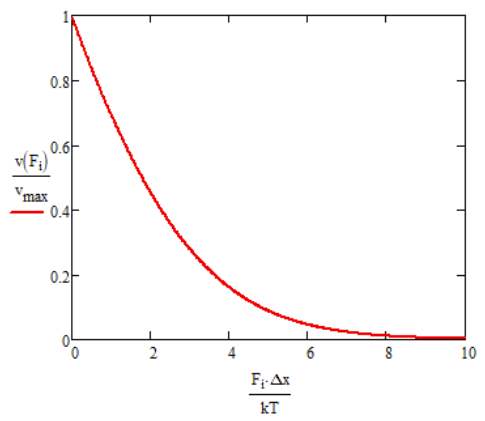
Now look at low force limit \(f \rightarrow 0 \). Expand \(e^{\underset{ \sim }{f}}=1+\underset{ \sim }{f}+\underset{ \sim }{f}^2/2 \):

\[ \langle \nu \rangle \rightarrow \dfrac{2D}{\Delta x} = v_{max} \nonumber \]

Note that this is the maximum velocity for ideal ratchet, and it follows the expected behavior for pure diffusive motion.

Now consider probability of the protein binding is governed by equilibrium between free and bound forms:

\[ F \overset{k_a}{\underset{k_d} \rightleftharpoons} B \qquad \qquad K= \dfrac{k_a}{k_d} = \dfrac{\tau_B}{\tau_F} \nonumber \]

Here k_a refers to the effecting quasi-first-order rate constant for binding at a chaperone concentration [chap]: \(k_a = k_a' [ chap ] \).

Fast kinetics approximation

\[ \begin{aligned} &\langle \nu \rangle = \dfrac{2D}{\Delta x} \left[ \dfrac{\underset{ \sim }{f}^2/2}{\dfrac{e^{\underset{ \sim }{f}}-1}{1-K(e^{\underset{ \sim }{f}}-1)}-\underset{ \sim }{f}} \right] \\ &\langle \nu \rangle_{max} = \dfrac{2D}{\Delta x} \left( \dfrac{1}{1+2K} \right) \end{aligned} \]

Stall Load

\[ f_0 = \dfrac{k_BT}{\Delta x} \ln \left( 1+ \dfrac{1}{K} \right) \nonumber \]

________________________________

1. C. S. Peskin, G. M. Odell and G. F. Oster, Cellular motions and thermal fluctuations: the Brownian ratchet, Biophys. J. 65 (1), 316–324 (1993).