17.3: Trinquete Browniano

El trinquete browniano se refiere a una clase de modelos para transporte dirigido utilizando movimiento browniano que se rectifica a través de la entrada de energía. Para una partícula difusa, la energía se utiliza para alternar entre dos estados que difieren en sus procesos de transporte difusivo. Este comportamiento da como resultado una difusión sesgada. Se aplica ampliamente para motores moleculares procesivos que se mueven entre estados discretos y, por lo tanto, es particularmente útil para comprender las proteínas motoras traduccionales y rotacionales.

Una observación común que encontramos es que el movimiento dirigido requiere que el objeto cambie entre dos estados que están acoplados a su movimiento, y para los cuales el intercambio es impulsado por la energía de entrada. El cambio entre estados da como resultado una difusión sesgada. La interpretación de los sistemas reales dentro del contexto de este modelo puede variar. Algunas personas consideran este ciclo como determinista, mientras que otras lo consideran bastante aleatorio y ruidoso, sin embargo, en cualquier caso, el movimiento browniano se aprovecha para mover la partícula.

Consideraremos un ejemplo relevante para el paso a paso alimentado por ATP de motores citoesqueléticos a lo largo de un filamento. Los ciclos motores entre dos estados: (1) un estado unido (B), para lo cual la proteína se une a un sitio particular en el filamento sobre sí mismo uniéndose a ATP, y (2) un estado libre (F) para el cual la proteína se difunde libremente a lo largo del filamento tras la hidrólisis de ATP y liberación de ADP + P _i. El estado unido se describe mediante un perfil energético periódico espacialmente asimétrico\(U_B(x)\), para lo cual la proteína se localiza a un mínimo de energía particular a lo largo del filamento. Las características clave de este potencial son una serie de sitios separados por una barrera\(ΔU > k_BT\), y una asimetría en cada pozo que desvía el sistema hacia un mínimo local en la dirección de desplazamiento. En el estado libre, no hay barreras para el movimiento y la proteína se difunde libremente. Cuando la proteína libre se une a otro ATP, vuelve\(U_B(x)\) y se relaja al mínimo de energía más cercano.

Investiguemos los factores que rigen el movimiento de la partícula en este trinquete browniano, utilizando la perspectiva de una caminata aleatoria sesgada. Los parámetros importantes para nuestro modelo son:

• La distancia entre los sitios de unión adyacentes es\(Δx\).
• La posición de la barrera delantera con respecto al sitio de unión es\(x_f\). Una barrera para la difusión inversa está en\(–x_r\), de modo que

\[x_f+x_r = \Delta x\]

La asimetría de\(U_B\) es descrita por

\[ \alpha =(x_f-x_r)/\Delta x \]

• El tiempo promedio que un trinquete permanece libre o atado son\(\tau_F\) y\(\tau_B\). Por lo tanto, el tiempo promedio por ciclo de unidad/liberación es

\[ \Delta t = \tau_F+\tau_B \nonumber \]

• Definimos una longitud de difusión\(\ell \) que depende del tiempo que la proteína está libre

\[ \ell_0(\tau_F)=\sqrt{4D\tau_F} \nonumber \]

Condiciones para un transporte eficiente

Consideremos las condiciones para maximizar la velocidad del trinquete browniano.

1. Mientras que en\(F\): el periodo óptimo para estar difundiendo libremente se rige por dos preocupaciones opuestas. Queremos que la partícula esté libre el tiempo suficiente para difundirse más allá de la barrera delantera, pero no tanto como para difundirse más allá de la barrera inversa. Por lo tanto, nos gustaría que la longitud de difusión se encontrara entre las distancias a estas barreras:

\[ \ell_0=\sqrt{4D\tau_F} \nonumber \]

\[ x_r > l_0 > x_F \nonumber \]

Usando el valor promedio como objetivo:

\[ \begin{aligned} \ell_0 &\approx \dfrac{x_r+x_F}{2}= \dfrac{\Delta x}{2} \\ \tau_F &\approx \dfrac{\Delta x^2}{16D} \end{aligned} \]

2. Mientras que en B: Después del ATP vinculante, nos gustaría que la partícula se quedara con ATP unido el tiempo suficiente para relajarse al mínimo del paisaje energético asimétrico. Compitiendo con esta consideración, no queremos que se mantenga atado más tiempo del necesario si la velocidad es el problema.

Podemos calcular el tiempo necesario para relajarnos de la barrera a x _r adelante al mínimo potencial, si conocemos la velocidad de deriva v _d de esta partícula bajo la influencia del potencial.

\[\tau_B \approx x_r/ \nu_d \nonumber \]

La velocidad de deriva está relacionada con la fuerza sobre la partícula a través del coeficiente de fricción\(\nu_d = f/\zeta \), y podemos obtener la magnitud de la fuerza a partir de la pendiente del potencial:

\[ |f| = \dfrac{\Delta U}{x_r} \nonumber \]

Entonces la velocidad de deriva es\(\nu_d = \dfrac{fD}{k_BT}= \dfrac{\Delta UD}{x_rk_BT} \) y el tiempo límite óptimo es

\[\tau_B \approx \dfrac{x_r^2k_BT}{\Delta UD} \nonumber \]

Ahora veamos esto un poco más cuidadosamente. Ahora podemos calcular la probabilidad de difusión hacia adelante sobre la barrera durante el intervalo libre integrando sobre la fracción de la población que se ha difuminado más allá de x _f durante τ _F. Usando la distribución de probabilidad difusiva con x0→0,

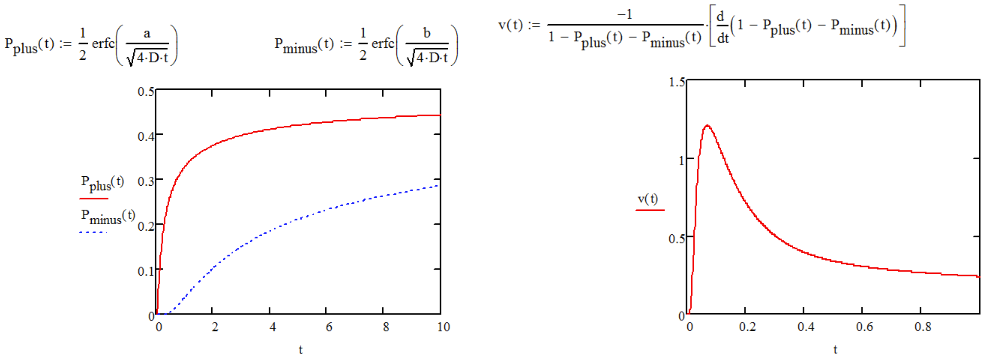
\[ \begin{aligned} P_+ &= \dfrac{1}{\sqrt{4\pi D\tau_F}} \int_{x_f}^{\infty} e^{-x^2/4D\tau_F} dx \\ &=\dfrac{1}{2} erfc\left( \dfrac{x_f}{\ell_0} \right) \end{aligned}\]

Del mismo modo, la probabilidad de difusión hacia atrás sobre la barrera a x = −x _r es

\[ P_- = \dfrac{1}{2} erfc \left( \dfrac{x_r}{\ell_0} \right) \nonumber \]

Ahora podemos determinar la velocidad promedio de la proteína calculando el desplazamiento promedio en un paso de tiempo dado. El desplazamiento promedio es la diferencia de probabilidad para tomar un paso adelante versus un paso inverso, multiplicado por el tamaño del paso. Este desplazamiento ocurre durante el intervalo de tiempo Δt. Por lo tanto,

\[ \begin{aligned} \nu &= \dfrac{\Delta P \Delta x}{\Delta t}\\ &=\dfrac{(P_+-P_-)\Delta x}{(\tau_B + \tau_F)} \\ &=\dfrac{\Delta x}{2\Delta t} \left[ erf\left( \dfrac{x_r}{\ell_0 (\tau_F)}\right) - erf \left( \dfrac{x_f}{\ell_0 (\tau_F)} \right) \end{aligned} \]

De esta expresión queda claro que la velocidad es cero cuando la asimetría del potencial es cero. Para los potenciales asimétricos, P ₊ y P _‒ dependen del τ _F, con uno aumentando en el tiempo más rápido que el otro. Como resultado, la velocidad, que depende de la diferencia de estos alcanza un máximo en las proximidades de\(\tau_F=x^2_f/D \).

Entonces, ¿cómo influye la hidrólisis de ATP en el gradiente de energía libre? Aquí el gradiente de energía libre es

\[ \dfrac{\Delta G_{Hyd.}}{\Delta x} \nonumber \]

\(k_+ = A_+e^{-(\Delta G_{barrier}-\Delta G_{hydrolysis})/kT} \)

\(k_- = A_-e^{-(\Delta G_{barrier})/kT} \)

\( \nu = (k_+-k_-) \Delta x \)

___________________________________________

K. Dill y S. Bromberg, Fuerzas Impulsoras Moleculares: Námica Termodía Estadística en Biología, Química, Física y Nanociencia. (Taylor & Francis Group, New Y ork, 2010); R. Phillips, J. Kon dev, J. Theriot y H. García, Physical Biology of the Cell, 2nd ed. (Taylor & Francis Group, Nueva York, 2012).