15.1: Definiciones

Última actualización
Guardar como PDF

Page ID: 70129

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

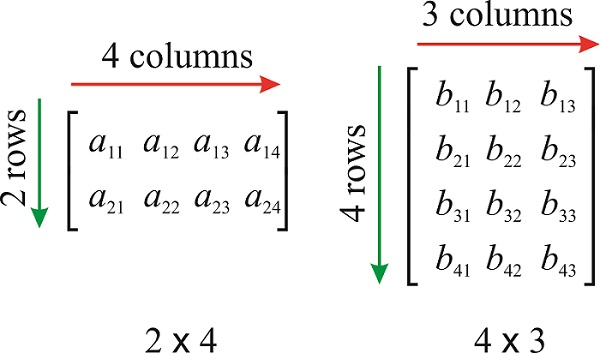
Una\(m\times n\) matriz\(\mathbf{A}\) es una matriz rectangular de números con\(m\) filas y\(n\) columnas. Los números\(m\) y\(n\) son las dimensiones de\(\mathbf{A}\). Los números en la matriz se llaman sus entradas. Se llama a la entrada en fila\(i\) y columna\(j\)\(a_{ij}\).

Figura\(\PageIndex{1}\): Matrices de diferentes dimensiones (CC BY-NC-SA; Marcia Levitus)

Algunos tipos de matrices tienen nombres especiales:

Una matriz cuadrada:\[\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \\ -i & 1/2 &9 \end{pmatrix} \nonumber\] con\(m=n\)
Una matriz rectangular:\[\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \end{pmatrix}\nonumber\] con\(m\neq n\)
Un vector de columna:\[\begin{pmatrix} 3 \\ 5\\ -i \end{pmatrix}\nonumber\] con\(n=1\)
Un vector de fila:\[\begin{pmatrix} 3 &-2 &4 \\ \end{pmatrix}\nonumber\] con\(m=1\)
La matriz de identidad:\[\begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0&0 &1 \end{pmatrix}\nonumber\] con\(a_{ij}=\delta_{i,j}\), donde\(\delta_{i,j}\) es una función definida como\(\delta_{i,j}=1\) if\(i=j\) y\(\delta_{i,j}=0\) if\(i\neq j\).
Una matriz diagonal:\[\begin{pmatrix} a &0 &0 \\ 0 &b &0 \\ 0&0 &c \end{pmatrix}\nonumber\] con\(a_{ij}=c_i \delta_{i,j}\).
Una matriz triangular superior:\[\begin{pmatrix} a &b &c \\ 0 &d &e \\ 0&0 &f \end{pmatrix}\nonumber\] Todas las entradas por debajo de la diagonal principal son cero.
Una matriz triangular inferior:\[\begin{pmatrix} a &0 &0 \\ b &c &0 \\ d&e &f \end{pmatrix}\nonumber\] Todas las entradas por encima de la diagonal principal son cero.
Una matriz triangular es aquella que es triangular inferior o triangular superior.

El rastro de una matriz

El rastro de una matriz\(n\times n\) cuadrada\(\mathbf{A}\) es la suma de los elementos diagonales, y formalmente definido como\(Tr( \mathbf{A})=\sum_{i=1}^{n}a_{ii}\).

Por ejemplo,

\[\mathbf{A}=\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \\ -i & 1/2 &9 \end{pmatrix}\; ; Tr(\mathbf{A})=12+3i \nonumber\]

Matrices Singulares y No Singulares

Una matriz cuadrada con determinante distinto de cero se llama nonsingular. Una matriz cuyo determinante es cero se llama singular. (Tenga en cuenta que no se puede calcular el determinante de una matriz no cuadrada).

La Transposición Matrix

La transposición matricial, más comúnmente escrita\(\mathbf{A}^T\), es la matriz obtenida mediante el intercambio\(\mathbf{A}\) de filas y columnas. Se obtiene reemplazando todos los elementos\(a_{ij}\) por\(a_{ji}\). Por ejemplo:

\[\mathbf{A}=\begin{pmatrix} 3 &-2 &4 \\ 5 &3i &3 \end{pmatrix}\rightarrow \mathbf{A}^T=\begin{pmatrix} 3 &5\\ -2 &3i\\ 4&3 \end{pmatrix} \nonumber\]