22.6.7: vi. Soluciones a Problemas
- Page ID
- 74513
-
Utilizaremos el software QMIC para hacer este problema. Vamos a empezar desde el principio. Obtener los coeficientes mo iniciales de “adivinar” en el disco. Usando el programa MOCOEFS nos pide los vectores primero y segundo mo. Ingresamos 1, 0 para el primer mo (esto significa que el primer mo es 1.0 veces el orbital He 1s más 0.0 veces el orbital H 1s; este mo de unión es más probable que esté fuertemente ponderado en el átomo que tiene la carga nuclear más alta) y 0, 1 para el segundo. Nuestra matriz mo-ao inicial se ve así:\ begin {bmatrix} 1.0 & 0.0\\ 0.0 & 1.0\ end {bmatrix} y se coloca en el disco en un archivo que elegimos llamar "mocoefs.dat”. También ponemos las integrales ao en disco usando el programa RW_INTS. Pide las integrales únicas de uno y dos electrones y coloca una lista canónica de éstas en disco en un archivo que elegimos llamar "ao_integrals.dat”. En este punto es útil para nosotros dar un paso atrás y mirar el conjunto de ecuaciones que deseamos resolver: FC = SCE. El software QMIC no nos proporciona un llamado solver de valores propios generalizados (uno que contiene una matriz de superposición; o métrica), por lo que para usar el programa de diagonalización que se proporciona debemos transformar esta ecuación (FC = SCE) en una que se vea como (F'C' = C'E). Lo hacemos de la siguiente manera:
Dado que S es simétrico y positivo definido podemos encontrar un\(S^{-\dfrac{1}{2}} \text{ such that } S^{-\dfrac{1}{2}} S^{+\dfrac{1}{2}} = 1, S^{-\dfrac{1}{2}} S = S^{+\dfrac{1}{2}}\), etc. reescribir FC = SCE insertando la unidad entre FC y multiplicando toda la ecuación de la izquierda por\( S^{-\dfrac{1}{2}} \). Esto da:
\[ S^{-\dfrac{1}{2}} FS^{-\dfrac{1}{2}}S^{+\dfrac{1}{2}} C = S^{-\dfrac{1}{2}} SCE = S^{+\dfrac{1}{2}}CE \]
Dejar:\ begin {align} F' &= S^ {-\ dfrac {1} {2}} FS^ {-\ dfrac {1} {2}}\\ C' &= S^ {+\ dfrac {1} {2}} C\ text {, e insertar expresiones arriba dan:}\\ F'C' &= C'E\ end {align}
Nota, que para obtener las siguientes iteraciones mo coeficientes debemos calcular C a partir de C':
C' =\(S^{+\dfrac{1}{2}}\) C, así, multiplicando a través de la izquierda por\(S^{-\dfrac{1}{2}}\) da:
\[ S^{-\dfrac{1}{2}}C' = S^{-\dfrac{1}{2}}S^{+\dfrac{1}{2}}C = C \]
Este será el método que usaremos para resolver nuestras ecuaciones de fock.
Encuentra\(S^{-\dfrac{1}{2}}\) usando el programa FUNCT_MAT (este programa genera una función de una matriz). Este programa solicitará los elementos de la matriz S y escribirá en el disco un archivo (nombre de su elección... un buen nombre podría ser “shalf”) que contenga la\(S^{-\dfrac{1}{2}}\) matriz. Ahora estamos listos para comenzar el procedimiento iterativo de Fock.
a. Calcula la matriz Fock, F, usando el programa FOCK que lee en los coeficientes mo de "mocoefs.dat" y las integrales de "ao_integrals.dat" y escribe la matriz Fock resultante en un archivo especificado por el usuario (un buen nombre de archivo para usar podría ser algo así como “fock1").
b. Calcular F' =\(S^{-\dfrac{1}{2}}FS^{-\dfrac{1}{2}}\) usando el programa UTMATU que lee en F y\(S^{-\dfrac{1}{2}}\) desde archivos en el disco y escribe F' en un archivo especificado por el usuario (un buen nombre de archivo para usar podría ser algo así como “fock1p”). Diagonalizar F' usando el programa DIAG. Este programa lee en la matriz para ser diagonalizado a partir de un nombre de archivo especificado por el usuario y escribe los vectores propios resultantes en el disco usando un nombre de archivo especificado por el usuario (un buen nombre de archivo para usar podría ser algo así como “coef1p”). Es posible que desee elegir la opción de escribir los valores propios (energías orbitales Fock) en el disco para utilizarlos posteriormente en el programa FENERGY. Calcular C transformando hacia atrás, por ejemplo, C =\(S^{-\dfrac{1}{2}}\) C'. Esto se logra usando el programa MATXMAT que lee en dos matrices que se multiplicarán a partir de archivos especificados por el usuario y escribe el producto en el disco usando un nombre de archivo especificado por el usuario (un buen nombre de archivo para usar podría ser algo así como "mocoefs.dat “).
c. El programa QMIC FENERGY calcula la energía total, utilizando el resultado de los ejercicios 2 y 3;
\[ \sum\limits_{kl} 2\langle k|h|k\rangle + 2\langle k1|1k \rangle - \langle k1|1k \rangle + \sum\limits_{\mu > \nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} \text{, and } \sum\limits_k \varepsilon_k + \langle k|h|k \rangle + \sum\limits_{\mu > \nu }\dfrac{Z_\mu Z_\nu}{R_{\mu\nu}}. \]
Esta es la conclusión de una iteración del procedimiento Fock... puedes continuar volviendo a la parte a. y avanzando.
d. y e. Los resultados para la convergencia exitosa de este sistema utilizando el software QMIC suministrado son los siguientes (esto es un gran detalle sangriento pero le dará al usuario la seguridad de que están en el camino correcto; alternativamente uno podría cambiar al programa QMIC SCF y permitir que programa para converger iterativamente las ecuaciones de Fock):
Las integrales AO de un electrón:
\[ \begin{bmatrix} -2.644200 & -1.511300 \\ -1.511300 & -1.720100 \end{bmatrix} \]
Las integrales AO de dos electrones:
\[ \begin{align} & 1 & & 1 & & 1 & & 1 & & 1.054700 & \\ & 2 & & 1 & & 1 & & 1 & & 0.4744000 & \\ & 2 & & 1 & & 2 & & 1 & & 0.5664000 & \\ & 2 & & 2 & & 1 & & 1 & & 0.2469000 & \\ & 2 & & 2 & & 2 & & 1 & & 0.3504000 & \\ & 2 & & 2 & & 2 & & 2 & & 0.6250000 & \end{align} \]
Los coeficientes MO-AO “iniciales”:
\[ \begin{bmatrix} 1.000000 & 0.000000 \\ 0.000000 & 1.000000 \end{bmatrix} \]
Matriz de superposición AO (S):
\[ \begin{bmatrix} 1.000000 & 0.578400 \\ 0.578400 & 1.000000 \end{bmatrix} \]
\[ S^{-\dfrac{1}{2}} \begin{bmatrix} 1.168032 & -0.3720709 \\ -0.3720709 & 1.168031 \end{bmatrix} \]
************
ITERACIÓN 1
************
La matriz de orden de bonos de carga
\[ \begin{bmatrix} 1.000000 & 0.000000 \\ 0.000000 & 0.000000 \end{bmatrix} \]
La matriz de Fock (F):
\[ \begin{bmatrix} -1.589500 & -1.036900 \\ -1.036900 & -0.8342001 \end{bmatrix} \]
\( S^{-\dfrac{1}{2}}FS^{-\dfrac{1}{2}} \)
\[ \begin{bmatrix} -1.382781 & -0.5048679 \\ -0.5048678 & -0.4568883 \end{bmatrix} \]
Los valores propios de esta matriz (energías orbitales de Fock) son:
\[ [ -1.604825 -0.2348450 ] \]
Sus correspondientes vectores propios (C =\(S^{+\dfrac{1}{2}}*C\)) son:
\[ \begin{bmatrix} -0.9153809 & -0.4025888 \\ -0.4025888 & 0.9153810 \end{bmatrix} \]
Los “nuevos” coeficientes MO-AO (C =\(S^{-\dfrac{1}{2}}\) *C')
\[ \begin{bmatrix} -0.9194022 & -0.8108231 \\ -0.1296498 & 1.218985 \end{bmatrix} \]
Las integrales MO de un electrón:
\[ \begin{bmatrix} -2.624352 & -0.1644336 \\ -0.1644336 & -1.306845 \end{bmatrix} \]
Las integrales MO de dos electrones:
\[ \begin{align} & 1 & & 1 & & 1 & & 1 & & 0.9779331 & \\ & 2 & & 1 & & 1 & &1 & & 0.1924623 & \\ & 2 & & 1 & & 2 & & 1 & & 0.5972075 & \\ & 2 & & 2 & & 1 & & 1 & & 0.1170838 & \\ & 2 & & 2 & & 2 & & 1 & & -0.0007945194 & \\ & 2 & & 2 & & 2 & & 2 & & 0.6157323 & \end{align} \]
La cáscara cerrada Fock energía de fórmula:
\[ \sum\limits_{kl} 2 \langle k|h|k \rangle + 2\langle k1|k1 \rangle - \langle k1|1k \rangle + \sum\limits_{\mu >\nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.84219933 \]
de fórmula:
\[ \sum\limits_k \varepsilon_k + \langle k|h|k \rangle + \sum\limits_{\mu > \nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.80060530 \]
la diferencia es:
\[ -0.04159403 \]
**** ********
ITERACIÓN 2
************
La matriz de orden de cambio de bonos:
\[ \begin{bmatrix} 0.8453005 & 0.1192003 \\ 0.1192003 & 0.01680906 \end{bmatrix} \]
La matriz de Fock:
\[ \begin{bmatrix} -1.624673 & -1.083623 \\ -1.083623 & -0.8772071 \end{bmatrix} \]
\( S^{-\dfrac{1}{2}}F S^{-\dfrac{1}{2}} \)
\[ \begin{bmatrix} -1.396111 & -0.5411037 \\ -0.5411037 & -0.4798213 \end{bmatrix} \]
Los valores propios de esta matriz (energías orbitales de Fock) son:
\[ [ -1.646972 -0.2289599 ] \]
Sus vectores propios correspondientes (C' =\(S^{+\dfrac{1}{2}}\) *C) son:
\[ \begin{bmatrix} -0.9072427 & -0.4206074 \\ -0.4206074 & 0.9072427 \end{bmatrix} \]
Los “nuevos” coeficientes MO-AO (C =\(S^{-\dfrac{1}{2}}\) *C'):
\[ \begin{bmatrix} -0.9031923 & -0.8288413 \\ -0.1537240 & 1.216184 \end{bmatrix} \]
Las integrales MO de un electrón:
\[ \begin{bmatrix} -2.617336 & -0.1903475 \\ -0.1903475 & -1.313861 \end{bmatrix} \]
Las integrales MO de dos electrones:
\[ \begin{align} & 1 & & 1 & & 1 & & 1 & & 0.9626070 & \\ & 2 & & 1 & & 1 & & 1 & & 0.1949828 & \\ & 2 & & 1 & & 2 & & 1 & & 0.6048143 & \\ & 2 & & 2 & & 1 & & 1 & & 0.1246907 & \\ & 2 & & 2 & & 2 & & 1 & & 0.003694540 & \\ & 2 & & 2 & & 2 & & 2 & & 0.6158437 & \end{align} \]
La energía de Fock de concha cerrada de fórmula:
\[ \sum\limits_{kl} 2\langle k|h|k\rangle + 2\langle kl|kl \rangle - \langle kl|lk \rangle + \sum\limits_{\mu > \nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.84349298 \]
de fórmula:
\[ \sum\limits_k \varepsilon_k + \langle k|h|k \rangle + \sum\limits_{\mu > \nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.83573675 \]
la diferencia es:
\[ -0.00775623 \]
************
ITERACIÓN 3
************
La matriz de orden de enlace de cambio:
\[ \begin{bmatrix} -1.631153 & -1.091825 \\ -1.091825 & -0.8853514 \end{bmatrix} \]
\( S^{-\dfrac{1}{2}}FS^{-\dfrac{1}{2}} \)
\[ \begin{bmatrix} -1.398951 & -0.5470731 \\ -0.5470730 & -0.4847007 \end{bmatrix} \]
Los valores propios de esta matriz (energías orbitales de Fock) son:
\[ [ -1.654745 -0.2289078 ] \]
Sus vectores propios correspondientes (C' = \(S^{+\dfrac{1}{2}}\)*C) son:
\[ \begin{bmatrix} -0.9058709 & -0.4235546 \\ -0.4235545 & 0.9058706 \end{bmatrix} \]
Los “nuevos” coeficientes MM-AO (C=S\( ^{-\dfrac{1}{2}} \) *C'):
\[ \begin{bmatrix} -0.9004935 & -0.8317733 \\ -0.1576767 & 1.215678 \end{bmatrix} \]
Las integrales MO de un electrón:
\[ \begin{bmatrix} -2.616086 & -0.1945811 \\ -0.1945811 & -1.315112 \end{bmatrix} \]
Las integrales MO de dos electrones:
\[ \begin{align} & 1 & & 1 & & 1 & &1 & & 0.9600707 & \\ & 2 & & 1 & & 1 & & 1 & & 0.1953255 & \\ & 2 & & 1 & & 2 & & 1 & & 0.6060572 & \\ & 2 & & 2 & & 1 & & 1 & & 0.1259332 & \\ & 2 & & 2 & & 2 & & 1 & & 0.004475587 & \\ & 2 & & 2 & & 2 & & 2 & & 0.6158972 & \end{align} \]
La cáscara cerrada Fock energía de fórmula:
\[ \sum\limits_{kl} 2\langle k|h|k\rangle + 2\langle kl|kl\rangle - \langle kl|lk\rangle + \sum\limits_{\mu > \nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu }} = -2.84353018 \]
a partir de fórmula:
\[ \sum\limits_k \varepsilon_k + \langle k|h|k \rangle + \sum\limits_{\mu > \nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.84225941 \]
la diferencia es:
\[ -0.00127077 \]
************
ITERACIÓN 4
************
La matriz de orden de bonos de carga:
\[ \begin{bmatrix} 0.8108885 & -1.093155 \\ -1.093155 & -0.8866909 \end{bmatrix} \]
La matriz de Fock:
\[ \begin{bmatrix} -1.632213 & -1.093155 \\ -1.093155 & -0.8866909 \end{bmatrix} \]
\( S^{-\dfrac{1}{2}}FS^{-\dfrac{1}{2}} \)
\[ \begin{bmatrix} -1.399426 & -0.5480287 \\ -0.5480287 & -0.4855191 \end{bmatrix} \]
Los valores propios de esta matriz (energías orbitales de Fock) son:
\[ [ -1.656015 -0.2289308 ] \]
Sus vectores propios correspondientes (C' =\(S^{+\dfrac{1}{2}}\) *C) son:
\[ \begin{bmatrix} -0.9056494 & -0.4240271 \\ -0.4240271 & 0.9056495 \end{bmatrix} \]
El “nuevo” MO-AO coeficientes (C =\( S^{-\dfrac{1}{2}}\) *C'):
\[ \begin{bmatrix} -0.9000589 & -0.8322428 // -0.1583111 & 1.215595 \end{bmatrix} \]
Las integrales MO de un electrón:
\[ \begin{bmatrix} -2.615881 & -0.1952594 \\ -0.1952594 & -1.315315 \end{bmatrix} \]
Las integrales MO de dos electrones:
\[ \begin{align} & 1 & & 1 & & 1 & & 1 & & 0.9596615 & \\ & 2 & & 1 & & 1 & & 1 & & 0.1953781 & \\ & 2 & & 1 & & 2 & & 1 & & 0.6062557 & \\ & 2 & & 2 & & 1 & & 1 & & 0.1261321 \\ & 2 & & 2 & & 2 & & 1 & & 0.004601604 & \\ & 2 & & 2 & & 2 & & 2 & & 0.6159065 & \end{align} \]
La concha cerrada Fock energía de fórmula:
\[ \sum\limits_{kl} 2\langle k|h|k\rangle + 2\langle kl|kl\rangle - \langle kl|lk\rangle + \sum\limits_{\mu >\nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.84352922 \]
de fórmula:
\[ \sum\limits_k \varepsilon_k + \langle k|h|k\rangle + \sum\limits_{\mu >\nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.84332418 \]
la diferencia es:
\[ -0.00020504 \]
************
ITERACIÓN 5
*** *********
La matriz de orden de bonos de carga:
\[ \begin{bmatrix} 0.8101060 & 0.1424893 \\ 0.1424893 & 0.02506241 \end{bmatrix} \]
La matriz de Fock:
\[ \begin{bmatrix} -1.632385 & -1.093368 \\ -1.093368 & -0.8869066 \end{bmatrix} \]
\( S^{-\dfrac{1}{2}}FS^{-\dfrac{1}{2}} \)
\[ \begin{bmatrix} -1.399504 & -0.5481812 \\ -0.5481813 & -0.4856516 \end{bmatrix} \]
Los valores propios de esta matriz ( Energías orbitales de Fock) son:
\[ [ -1.656219 -0.2289360 ] \]
Sus vectores propios correspondientes (C' = S\(^{+\dfrac{1}{2}}\) *C) son:
\[ \begin{bmatrix} -0.9056138 & -0.4241026 \\ -0.4241028 & 0.9056141 \end{bmatrix} \]
Los “nuevos” coeficientes MO-AO (C =\(S^{-\dfrac{1}{2}}\) *C'):
\[ \begin{bmatrix} -0.8999892 & -0.8323179 \\ -0.1584127 & 1.215582 \end{bmatrix} \]
El integrales MO de un electrón:
\[ \begin{bmatrix} -2.615847 & -0.1953674 \\ -0.1953674 & -1.315348 \end{bmatrix} \]
Las integrales MO de dos electrones:
\[ \begin{align} & 1 & & 1 & & 1 & & 1 & & 0.9595956 & \\ & 2 & & 1 & & 1 & & 1 & & 0.1953862 & \\ & 2 & & 1 & & 2 & & 1 & & 0.6062872 & \\ & 2 & & 2 & & 1 & & 1 & & 0.1261639 & \\ & 2 & & 2 & & 2 & & 1 & & 0.004621811 & \\ & 2 & & 2 & & 2 & & 2 & & 0.6159078 & \end{align} \]
La energía de Fock de concha cerrada de fórmula: a
\[ \sum\limits_{kl} 2\langle k|h|k\rangle + 2\langle kl|kl\rangle - \langle kl|lk \rangle + \sum\limits_{\mu > \nu} \dfrac{Z_{\mu}Z_\nu}{R_{\mu\nu}} = -2.84352779 \]
partir de la fórmula:
\[ \sum\limits_k \varepsilon_k + \langle k|h|k\rangle + \sum\limits_{\mu > \nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.84349489 \]
la diferencia es:
-0.00003290
************
ITERACIÓN 6
************
La matriz de orden de fianza de carga:
\[ \begin{bmatrix} 0.8099805 & 0.1425698 \\ 0.1425698 & 0.02509460 \end{bmatrix} \]
La matriz de Fock:
\[ \begin{bmatrix} -1.632412 & -1.093402 \\ -1.093402 & -0.8869413 \end{bmatrix} \]
\( S^{-\dfrac{1}{2}}FS^{-\dfrac{1}{2}} \)
\[ \begin{bmatrix} -1.399517 & -0.5482056 \\ -0.5482056 & -0.4856730 \end{bmatrix} \]
Los valores propios de esta matriz (energías orbitales de Fock) son:
\[ [ -1.656253 -0.2289375 ] \]
Sus correspondientes vectores propios (C' =\(S^{+\dfrac{1}{2}}\) *C) son:
\[ \begin{bmatrix} -0.9056085 & -0.4241144 \\ -0.4241144 & 0.9056086 \end{bmatrix} \]
Los “nuevos” coeficientes MO-AO (C =\(S^{-\dfrac{1}{2}}\) *C'):
\[ \begin{bmatrix} 0.8999786 & -0.8323296 \\ -0.1584283 1.215580 \end{bmatrix} \]
Las integrales MO de un electrón:
\[ \begin{bmatrix} -2.615843 & -0.1953846 \\ -0.1953846 & -1.315353 \end{bmatrix} \]
El MO de dos electrones integrales:
\[ \begin{align} & 1 & & 1 & & 1 & & 1 & & 0.9595859 & \\ & 2 & & 1 & & 1 & & 1 & & 0.1953878 & \\ & 2 & & 1 & & 2 & & 1 & & 0.6062925 & \\ & 2 & & 2 & & 2 & & 1 & & 0.004625196 & \\ & 2 & & 2 & & 2 & & 2 & & 0.6159083 & \end{align} \]
La cáscara cerrada Energía de Fock de fórmula:
\[ \sum\limits_{kl} 2\langle k|h|k\rangle 2 \langle kl|kl\rangle - \langle kl|lk\rangle + \sum\limits_{\mu >\nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.84352827 \]
a partir de fórmula:
\[ \sum\limits_k \varepsilon_k + \langle k|h|k\rangle + \sum\limits_{\mu > \nu } \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.84352398 \]
la diferencia es:
-0.00000429
************
ITERACIÓN 7
************
La matriz de orden de bonos de carga:
\[ \begin{bmatrix} 0.8099616 & 0.1425821 \\ 0.1425821 & 0.02509952 \end{bmatrix} \]
La matriz de Fock:
\[ \begin{bmatrix} -1.632416 & -1.093407 \\ -1.093407 & -0.8869464 \end{bmatrix} \]
\( S^{-\dfrac{1}{2}}FS^{-\dfrac{1}{2}} \)
\[ \begin{bmatrix} -1.399519 & -0.5482093 \\ -0.5482092 & -0.4856761 \end{bmatrix} \]
Los valores propios de esta matriz (energías orbitales de Fock) son:
\[ [ -1.656257 -0.2289374 ] \]
Sus vectores propios correspondientes (C' =\(S^{+\dfrac{1}{2}}\) *C) son:
\[ \begin{bmatrix} -0.9056076 & -0.4241164 \\ -0.4241164 & 0.9056077 \end{bmatrix} \]
Los “nuevos” Coeficientes MO-AO (C=\(S^{-\dfrac{1}{2}}\) *C'):
\[ \begin{bmatrix} -0.8999770 & -0.8323317 \\ -0.1584310 & 1.215580 \end{bmatrix} \]
Las integrales MO de un electrón:
\[ \begin{bmatrix} -2.615843 & -0.1953876 \\ -0.1953876 & -1.315354 \end{bmatrix} \]
Las integrales MO de dos electrones:
\[ \begin{align} & 1 & & 1 & & 1 & & 1 & & 0.9595849 & \\ & 2 & & 1 & & 1 & & 1 & & 0.1953881 & \\ & 2 & & 1 & & 2 & & 1 & & 0.6062936 & \\ & 2 & & 2 & & 1 & & 1 & & 0.1261697 & \\ & 2 & & 2 & & 2 & & 1 & & 0.004625696 & \\ & 2 & & 2 & & 2 & & 2 & & 0.6159083 & \end{align} \]
La energía de Fock de concha cerrada a partir de la fórmula:
\[ \sum\limits_{kl} 2 \langle k|h|k\rangle + 2\langle kl|kl \rangle - \langle kl|lk \rangle + \sum\limits_{\mu > \nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.84352922 \]
de fórmula:
\[ \sum\limits_k \varepsilon_k + \langle k|h|k\rangle + \sum\limits_{\mu >\nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.84352827 \]
la diferencia es:
\[ -0.00000095 \]
************
ITERACIÓN 8
************
La matriz de orden de enlace de carga:
\[ \begin{bmatrix} 0.8099686 & 0.1425842 \\ 0.1425842 & 0.02510037 \end{bmatrix} \]
La matriz de Fock:
\[ \begin{bmatrix} -1.632416 & -1.093408 \\ -1.093408 & -0.8869470 \end{bmatrix} \]
\( S^{-\dfrac{1}{2}}FS^{-\dfrac{1}{2}} \)
\[ \begin{bmatrix} -1.399518 & -0.5482103 \\ -0.5482102 & -0.4856761 \end{bmatrix} \]
Los valores propios de esta matriz (Fock energías orbitales) son:
\[ [ -1.656258 -0.2289368 ] \]
Sus vectores propios correspondientes (C'=\(S^{+\dfrac{1}{2}}\) *C) son:
\[ \begin{bmatrix} -0.9056074 & -0.4241168 \\ -0.4241168 & 0.9056075 \end{bmatrix} \]
Los “nuevos” coeficientes MO-AO (C=\(S^{-\dfrac{1}{2}}\) *C'):
\[ \begin{bmatrix} -0.8999765 & -0.8323320 \\ -0.1584315 & 1.215579 \end{bmatrix} \]
El uno- Integrales MO de electrones:
\[ \begin{bmatrix} -2.615842 & -0.1953882 \\ -0.1953882 & -1.315354 \end{bmatrix} \]
Las integrales MO de dos electrones:
\[ \begin{align} & 1 & & 1 & & 1 & & 1 & & 0.9595841 & \\ & 2 & & 1 & & 1 & & 1 & & 0.1953881 & \\ & 2 & & 1 & & 2 & & 1 & & 0.6062934 & \\ & 2 & & 2 & & 1 & & 1 & & 0.1261700 & \\ & 2 & & 2 & & 2 & & 1 & & 0.004625901 & \\ & 2 & & 2 & & 2 & & 2 & & 0.6159081 & \end{align} \]
La energía de Fock de concha cerrada a partir de la fórmula: a
\[ \sum\limits_{kl} 2\langle k|h|k\rangle + 2 \langle kl|kl\rangle - \langle kl|lk\rangle + \sum\limits_{\mu > \nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.84352827 \]
partir de la fórmula:
\[ \sum\limits_k \varepsilon_k + \langle k|h|k\rangle + \sum\limits_{\mu >\nu} \dfrac{Z_\mu Z_\nu}{R_{\mu\nu}} = -2.84352827 \]
la diferencia es:
\[ 0.00000000 \]
f. Al mirar la convergencia energética vemos lo siguiente:
Iteración Fórmula 1 Fórmula 2 1 -2.84219933 -2.80060530 2 -2.84349298 -2.83573675 3 -2.84353018 -2.84225941 4 -2.84352922 -2.84332418 5 -2.84352779 -2.84349489 6 -2.84352827 -2.84352827 7 -2.84352922 -2.84352827 8 -2.84352827 -2.84352827 f. Si observas la diferencia de energía (SCF en la iteración n - SCF convergente) y trazas estos datos frente al número de iteración, y haces un ajuste polinomial de 5to orden, vemos lo siguiente:
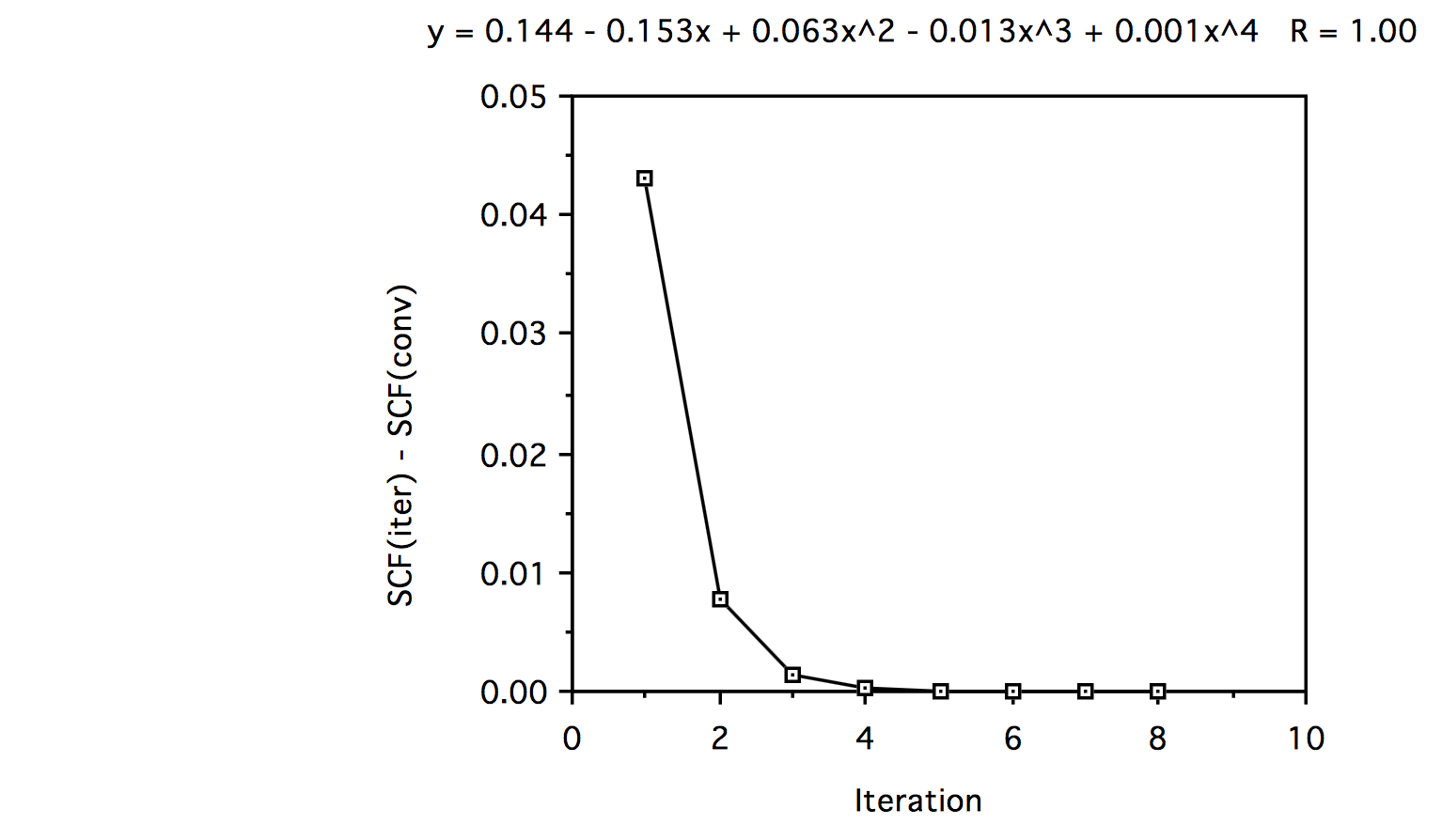
Al mirar el ajuste polinómico vemos que la convergencia es principalmente lineal ya que el coeficiente del término lineal es mucho mayor que los de los términos cúbicos y superiores.
g. La energía total de SCF convergente calculada usando el resultado del ejercicio 3 es un límite superior a la energía del estado fundamental, pero, durante el procedimiento iterativo no lo es. En la convergencia, el valor de expectativa del hamiltoniano para el determinante Hartree Fock viene dado por la ecuación en el ejercicio 3.
h. Las integrales de uno y dos electrones en la base MO se dan anteriormente (ver parte e iteración 8). Las energías orbitales se encuentran usando el resultado del ejercicio 2 y 3 para ser:
\ begin {align} E (SCF) &=\ sum\ limits_k\ varepsilon_k +\ langle k|h|k\ rangle +\ sum\ limits_ {\ mu >\ nu}\ dfrac {Z_\ mu Z_\ nu} {R_ {\ mu\ nu}\ E (SCF) &=\ suma\ límites_ {kl} 2\ langle k|h|k\ rangle + 2\ langle kl|kl\ rangle - \ langle kl|lk\ rangle +\ suma\ límites_ {\ mu >\ nu}\ dfrac {Z_\ mu Z_\ nu} {R_ {\ mu\ nu}}\\\ text {so,}\ varepsilon_k &=\ langle k|h|k\ rangle +\ sum\ límites_1^ {occ} (2\ langle kl|kl\ rangle -\ langle kl|lk\ rangle)\\\ varepsilon_1 &= h_ {11} + 2\ langle 11|11\ rangle -\ langle 11|11\ rangle\\ &= -2.615842 + 0. 9595841\\ &= -1.656258\\\ varepsilon_2 &= h_ {22} + 2\ langle 21|21\ rangle -\ langle 21|12\ rangle\\ &= -1.315354 + 2*0.6062934 - 0.1261700\\ &= -0.2289372\ end {align}
i. Sí, la\(\sigma^2\) configuración 1 se disocia correctamente porque en\( R\rightarrow \infty\) el más bajo estado energético es He +\(H^+\), que también tiene una ocupación\( 1\sigma^2\) orbital (es decir,\(1s^2\) en He y\(1s^0 \text{ on } H^+\)).
-
En convergencia los coeficientes mo son:
\[ \phi_1 = \begin{bmatrix} & -0.8999765 \\ & -0.1584315 \end{bmatrix} \phi_2 = \begin{bmatrix} & -0.8323320 \\ & 1.215579 \end{bmatrix} \]
y las integrales en esta base MO son:
\ begin {align} & h_ {11} = -2.615842 & & h_ {21} = -0.1953882 & & h_ {22} = -1.315354 &\\ & g_ {1111} = 0.9595841 & & g_ { 2111} = 0.1953881 & & g_ {2121} = 0.6062934 &\\ & g_ {2211} = 0.1261700 & & g_ {2221} = 004625901 & & g_ {2222} = 0.6159081 &\ end {align}
a.\ begin {align} H &=\ begin {bmatrix}\ langle 1\ Sigma^2|H|1\ sigma^2\ rangle &\ langle 1\ sigma^2|h|2\ sigma^2\ rangle\\\ langle 2\ sigma^2|h|h|1\ sigma^2\ rangle &\ langle 2\ sigma^2|H|2\ sigma^2\ rangle\ end {bmatrix} =\ begin {bmatrix} 2h_ {11} + g_ {1111} & g_ {1122}\\ g_ {1122} & 2h_ {22} + g_ {2222}\ end {bmatrix}\\ &=\ begin {bmatrix} 2*-2.615842 + 0.9595841 & 0.1261700\\ 0.126170 & 2*-1.315354 + 0.6159081\ end {bmatrix}\\ & =\ begin {bmatrix} -4.272100 & 0.126170\\ 0.126170 & -2.014800\ end {bmatrix}\ end {align}
b. Los autovalores son\(E_1 = -4.279131 \text{ and } E_2 = -2.007770.\) Los vectores propios correspondientes son:
\[ C_1 = \begin{bmatrix} & -.99845123 \\ & 0.05563439 \end{bmatrix} \text{ , C_2 = } \begin{bmatrix} & 0.05563438 \\ & 0.99845140 \end{bmatrix} \]
c.\ begin {align}\ dfrac {1} {2} &\ izquierda [\ big|\ izquierda (\ sqrt {a}\ phi_1 +\ sqrt {b}\ phi_2\ derecha)\ alpha\ izquierda (\ sqrt {a}\ phi_1 -\ sqrt {b}\ phi_2\ derecha)\ beta\ big| +\ big|\ left (\ sqrt(click for details)\ phi_2\ derecha)\ izquierda (\ sqrt {a}\ phi_1 +\ sqrt {b}\ phi_2\ derecha)\ derecha] (\ alpha\ beta -\ beta\ alpha)\\ &=\ dfrac {1} {\ sqrt {2}} (a\ phi_1\ phi_1 - b\ phi_2\ phi_2) (\ alpha\ beta -\ beta\ alpha)\\ &= a|\ phi_1\ alpha\ phi_1\ beta | - b|\ phi_2\ alpha\ phi_2\ beta |. &\ text {(nota de la parte b. a = 0.9984 y b = 0.0556)}\ end {align}Callstack: at (Quimica/Química_Física_y_Teórica/Libro:_Mecánica_cuántica_en_química_(Simons_y_Nichols)/22:_Problemas/22.06:_Aspectos_más_cuantitativos_de_los_cálculos_de_estructuras_electrónicas/22.6.07:_vi._Soluciones_a_Problemas), /content/body/ol/li/ol/li[1]/p[1]/span[4], line 1, column 2
d. La tercera configuración\( |1\sigma 2\sigma | = \dfrac{1}{\sqrt{2}} \left[ |1\alpha 2\beta | - | 1 \beta 2\alpha | \right]\),
Agregar esta configuración al CI 2x2 anterior da como resultado el siguiente CI 3x3 'full':
\ begin { align} H &=\ begin {bmatrix}\ langle 1\ sigma^2 |H|1\ sigma^2\ rangle &\ langle 1\ sigma^2 |H|H|2\ sigma^2\ rangle &\ langle 1\ sigma^2 |H|1\ sigma 2\ sigma\ rangle\\ langle 2\ sigma^2 |H|1\ sigma^^2\ rangle &\ langle 2\ sigma^2 |H|2\ sigma^2\ rangle &\ langle 2\ sigma^2 |H|1\ sigma 2\ sigma\ rangle\\ langle 1\ sigma 2\ sigma |H|1\ sigma^2\ rangle &\ langle 2\ sigma^2 |H|1\ sigma 2\ sigma\ rangle &\ langle 1\ sigma 2\ sigma |H|1\ sigma 2\ sigma\ rangle\ end {bmatrix}\\ &=\ begin {bmatrix} 2h_ {11} + g_ {1111} & g_ {1_ 122} &\ dfrac {1} {\ sqrt {2}}\ izquierda [2h_ {12} + 2g_ {2111}\ derecha]\\ g_ {1122} & 2h_ {22} + g_ {2222} & amp;\ dfrac {1} {\ sqrt {2}}\ izquierda [2h_ {12} + 2g_ {2221}\ derecha]\\ dfrac {1} {\ sqrt {2}}\ izquierda [2h_ {12} + 2g_ {2111}\ derecha] &\ dfrac {1} {\ sqrt {2}}\ izquierda [2h_ {12} + 2g_ {2221}\ derecha] & h_ {11} + h_ {22} + g_ {2121} + g_ {2211}\ end {bmatrix}\ end {align}
Evaluando lo nuevo elementos de la matriz:
\ begin {align} H_ {12} &= H_ {21} =\ sqrt {2} * (-0.1953882 + 0.1953881) = 0.0\\ H_ {23} &= H_ {32} =\ sqrt {2} * (-0.1953882 + 0.004626) = -0.269778\\ H_ {33} &= -2.615842 - 1.315354 + 0.606293 + 0.126170\\ &= -3.198733\\ &=\ begin {bmatrix} -4.272100 & 0. 126170 & 0.0\\ 0.126170 & -2.014800 & -0.269778\\ 0.0 & -0.269778 & -3.198733\ end {bmatrix}\ end {align}
e. Los autovalores son\( E_1 = -4.279345 \text{, } E_2 = -3.256612 \text{ and } E_3 = -1.949678.\) Los vectores propios correspondientes son:
\[ \begin{bmatrix} & -0.99825280 \\ & 0.05732290 \\ & 0.01431085 \end{bmatrix} \text{ , }C_2 = \begin{bmatrix} & -0.05302767 \\ & -0.20969283 \\ & -0.9774200 \end{bmatrix} \text{ , }C_3 = \begin{bmatrix} & -0.05302767 \\ & -0.97608540 \\ & 0.21082004 \end{bmatrix} \]
f.Necesitamos los elementos de matriz que no se desvanecen del operador dipolo en base mo. Estos se pueden obtener calculándolos a mano. Se obtienen más fácilmente mediante el uso del programa TRANS. Poner las integrales\(1e^-\) ao en el disco ejecutando el programa RW_INTS. En este caso está insertando\(z_{11} = 0.0 \text{, } z_{21} = 0.2854\text{, and } z_{22} = 1.4\) (inserte 0.0 para todas las\(2e^-\) integrales)... llame al archivo de salida “ao_dipole.ints” por ejemplo. Los coeficientes MO-AO convergentes deben estar en un archivo (” mocoefs.dat "está bien). Las integrales transformadas se pueden escribir en un archivo (nombre de su elección) por ejemplo “mo_dipole.ints”. Estos elementos de matriz son:
\[ Z_{11} = 0.11652690 \text{, } z_{21} = -0.54420990 \text{, } z_{22} = 1.49117320 \]
Las energías de excitación son\(E_2 - E_1 = -3.256612 - -4.279345 = 1.022733 \text{, and } E_3 - E_1 = -1.949678 .- - 4.279345 = 2.329667.\)
Usando las reglas de Slater-Conden para obtener los elementos de la matriz entre configuraciones obtenemos:
\ begin {align} H_z &=\ begin {bmatrix}\ langle 1\ sigma^2 |z| 1\ sigma^2\ rangle &\ langle 1\ sigma^2 |z| 2\ sigma^2\ rangle &\ langle 1\ sigma^2 |z|\ sigma 2\ sigma\ rangle\\ langle 2\ sigma^2 |z| 1\ sigma^2\ rangle &\ langle 2\ sigma^2 |z| | 2\ sigma^2\ rangle &\ langle 2\ sigma^2 |z| 1\ sigma 2\ sigma\ rangle\\ langle 1\ sigma 2\ sigma |z| 1\ sigma^2\ rangle &\ langle 2\ sigma^2 |z| 1\ sigma 2\ sigma\ rangle &\ langle 1\ sigma 2\ sigma |z| 1\ sigma 2\ sigma\ rangle\ end {bmatrix}\\ &=\ begin {bmatrix} 2z_ {11} & 0 &\ dfrac {1} {\ sqrt {2}}\ izquierda [2z_ {12}\ derecha]\\ 0 & 2z_ {22} &\ dfrac {1} {\ sqrt {2}}\ izquierda [2z_ {12}\ derecha]\\ dfrac {1} {\ sqrt {2}}\ izquierda [ 2z_ {12}\ derecha] &\ dfrac {1} {\ sqrt {2}}\ izquierda [2z_ {12}\ derecha] & z_ {11} + z_ {22}\ end {bmatrix}\\ begin {bmatrix} 0.233054 & 0 & -0.769629\\ 0 & 2.982346 & -0.769629\ -0.769629 629 & -0.769629 & 1.607700\ end {bmatrix}\ end {align}
Ahora,\( \langle \Psi_1 |z| \Psi_2 \rangle = C_1^TH_zC_2 \), (esto puede ser logrado con el programa UTMATU)
\ begin {align} &=\ begin {bmatrix} &-0.99825280\\ & 0.05732290\\ & 0.01431085\ end {bmatrix} ^T\ begin {bmatrix} 0.233054 & 0 & -0.769629\\ 0 & 2.982346 & -0.769629 & -0.769629 & 1.607700\ fin {bmatrix} \ begin {bmatrix} & -0.02605343\ & -0.20969283\\ & -0.9774200\ end {bmatrix}\\ &= -0.757494\ end {align}
y,\( \langle \Psi_1 |z| \Psi_3 \rangle = C_1^T H_zC_3\)
\ begin {align} &=\ begin {bmatrix} & -0.99825280\ & 0.05732290\\ & 0.01431085\ end {bmatrix} ^T\ begin {bmatrix} 0.233054 & 0 & -0.769629\\ 0 & 2.982346 & -0.769629\\ -0.769629 & -0.769629 & 1.607700\ end {bmatrix}\ begin {bmatrix} & -0.05302767\ & -0.97698540\\ & 0.21082004\ end {bmatrix}\ end align {}
g.Usando los coeficientes convergentes las energías orbitales obtenidas de resolver las ecuaciones de Fock son\(\varepsilon_1 = -1.656258 \text{ and } \varepsilon_2 = -0.228938.\) La expresión resultante para la función de onda de primer orden RSPT se convierte en:
\ begin {align}\ big| 1\ sigma^2\ rangle^ {(1)} &= -\ dfrac {g_ {2211}} {2 (\ varepsilon_2 -\ varepsilon_1)}\ big| 2\ sigma^2\ rangle\\\ big| 1\ sigma^2\ rangle^ {(1)} &= -\ dfrac {0.126170} {2 (-0.228938 + 1.656258)}\ big|2\ sigma^2\ rangle\\ big| 1\ sigma^2\ rangle^ {(1)} &= -0.0441982\ | 2\ sigma^2\ rangle\ end {align}
h. Como puedes ver en la parte c., la matriz \( \langle 1\sigma^2 |H| 1\sigma 2\sigma\rangle = 0\)(esto también es resultado del teorema de Brillouin) y por lo tanto esta configuración no entra en la función de onda de primer orden.
i.\ begin {align} &\ big| 0\ rangle =\ big| 1\ sigma^2\ rangle - 0.0441982\ big| 2\ sigma^2\ rangle. \ text {Para normalizar dividimos por:}\\ &\ sqrt {\ left [1 + (0.0441982) ^2\ derecha]} = 1.0009762\ &\ big|0\ rangle = 0.999025\ big| 1\ sigma^2\ rangle - 0.044155\ big| 2\ sigma^2\ rangle\ end {align}
En el CI 2x2 obtuvimos:
\ begin {align} &\ big|0\ rangle = 0.99845123 \ big| 1\ sigma^2\ rangle - 0.05563439\ big| 2\ sigma^2\ rangle\ end {align}
j. La expresión para el\(2^{nd}\) orden RSPT es:
\ begin {align} E^ {(2)} &= -\ dfrac {|g_ {2211} |^2} {2 (\ varepsilon_2 -\ varepsilon_2 -\ varepsilon_2 -\ varepsilon_2 on_1)} = -\ dfrac {0.126170^2} { 2 (-0.228938 + 1.656258)}\\ &= -0.005576\ text {au}\ end {align}
Comparando la energía de CI 2x2 obtenida con el resultado SCF tenemos:
-4.279131 - (-4.272102) = -0.007029 au
-
\ begin {align} &\ text {energía total STO:} & -2.8435283\\ &\ text {energía total STO3G} & -2.8340561\\ &\ texto {3-21G energía total} & -2.8864405\ end {align}
Los orbitales STO3G se generaron como un mejor ajuste de 3 gaussianos primitivos (dando 1 CGTO) al STO. Entonces, STO3G puede en el mejor de los casos reproducir el resultado STO. Los orbitales 3-21G son más flexibles ya que hay 2 CGTO por átomo. Esto da 4 orbitales (más parámetros para optimizar) y una menor energía total.
-
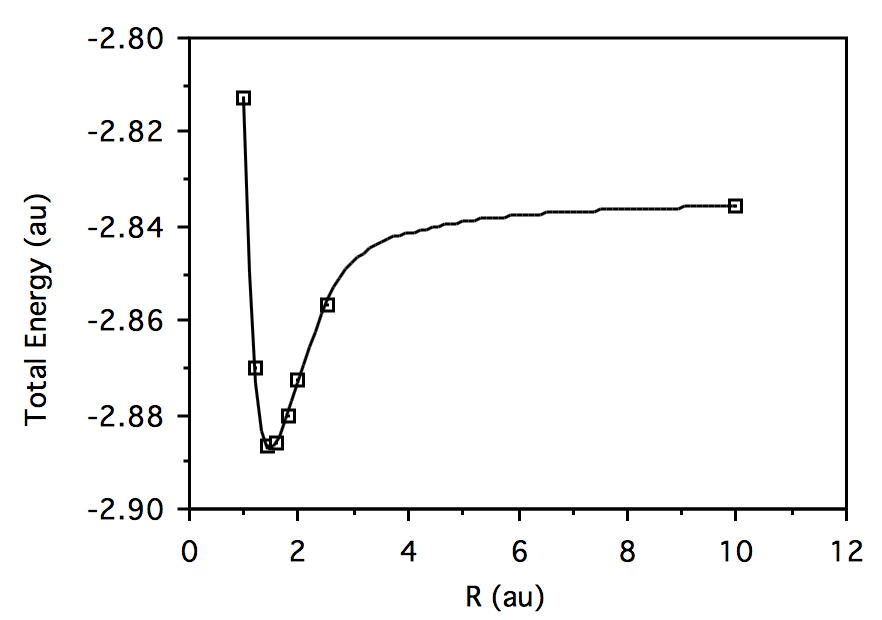
R \(HeH^+\)Energía \(H_2\)Energía 1.0
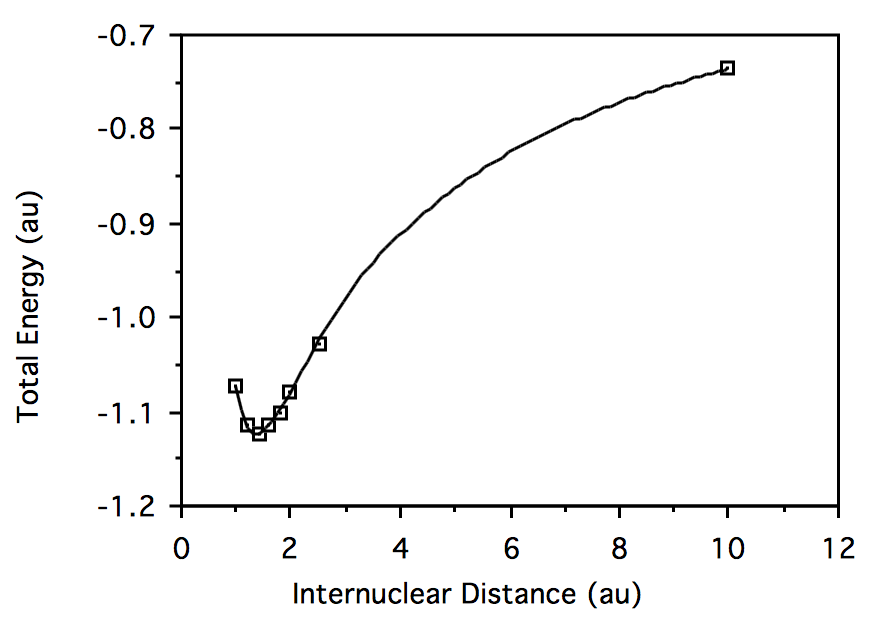
-2.812787056 -1.071953297 1.2 -2.870357513 -1.113775015 1.4 -2.886440516 -1.122933507 1.6 -2.886063576 -1.115567684 1.8 -2.880080938 -1.099872589 2.0 -2.872805595 -1.080269098 2.5 -2.856760263 -1.026927710 10.0 -2.835679293 -0.7361705303 Trazar energía total vs. geometría para\( HeH^+:\)
Trazar energía total vs. geometría para\(H_2:\)
For\(HeH^+\) a R = 10.0 au, los valores propios de la matriz convergente de Fock y la correspondientes coeficientes MO-AO convergentes son:
\ begin {align} -0.1003571E+01 & -0.4961988E+00 & 0.5864846E+00 & 0.1981702E+01\\ 0.4579189E+00 & -0.8245406E-05 & 0.1532163E-04 & 0.1157140E+01\\ 0.6572777E+00 & -0.4580946E-05 & -0. 6822942E-05 & -0.1056716E+01\\ -0.1415438E-05 & 0.3734069E+00 & 0.1255539E+01 & -0.1669342E-04\\ 0.1112778 & 0.71732444E+00 & -0.1096019E01 & 0.2031348E04\ end {align}
Observe que esto indica que orbital 1 es una combinación de los s funciones en Él solamente (disociándose adecuadamente a\( He + H^+\)).
Para\(H_2 \text{ at } R = 10.0\) au, los valores propios de la matriz convergente de Fock y los coeficientes MO-AO convergentes correspondientes son:
\ begin {align} -0.2458041E+00 & -0.1456223E+00 & 0.1137235E+01 & 0.1137825E+01\\ 0.1977649E+00 & -0.1978204E+00 & 0.1006458E+01 & -0.7903225E+00\\ 0.56325666E+00 & -0.5628273E+00 & -0.8179120E+00 & 0.6424941E+00\\ 0.1976312E+00 & 0.1979216E+00 & 0.7902887E+00 & 0.1006491E+01\ 0.5629326E+00 & 0.5631776E+00 & -0.6421731E+00 & -0.6421731E+00 & amp; -0.8181460E+00\ end {align}
Observe que esto indica que el orbital 1 es una combinación de las funciones s en ambos átomos de H (disociarse incorrectamente; probabilidades iguales de\(H_2\) disociarse a dos átomos neutros o a un protón más ion hidruro).
- El resultado de\(H_2\) CI”
R \(^1\sum_g^+\) \(^3\sum_u^+\) \(^1\sum_u^+\) \(^1\sum_g^+\) 1.0 -1.074970 -0.5323429 -0.3997412 0.3841676 1.2 -1.118442 -0.6450778 -0.4898805 0.1763018 1.4 -1.129904 -0.7221781 -0.5440346 0.0151913 1.6 -1.125582 -0.7787328 -0.5784428 -0.1140074 1.8 -1.113702 -0.8221166 -0.6013855 -0.2190144 2.0 -1.098676 -0.8562555 -0.6172761 -0.3044956 2.5 -1.060052 -0.9141968 -0.6384557 -0.4530645 5.0 -0.9835886 -0.9790545 -0.5879662 -0.5802447 7.5 -0.9806238 -0.9805795 -0.5247415 -0.5246646 10.0 -0.989598 -0.9805982 -0.4914058 -0.4913532 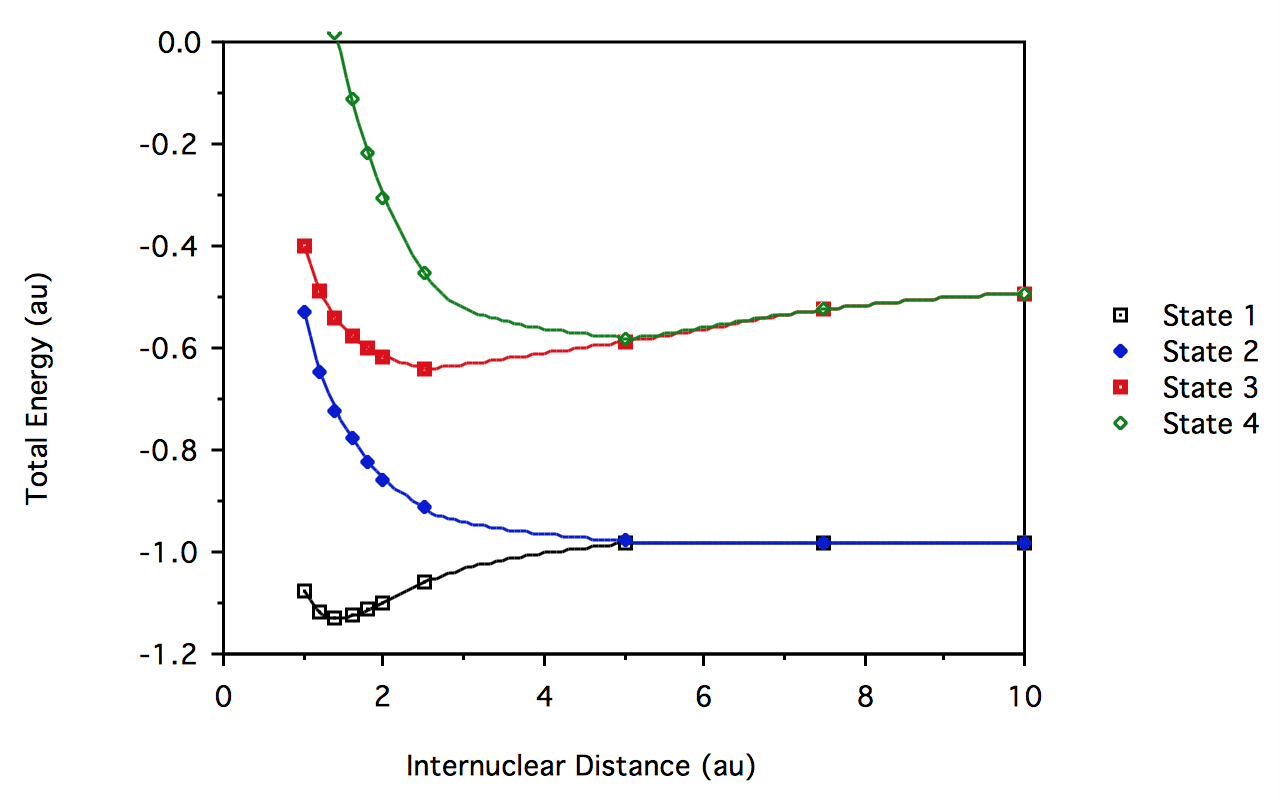
Para\(H_2\) a R = 1.4 au, los valores propios de la matriz hamiltoniana y las correspondientes amplitudes determinantes son:
determinante -1.129904 -0.722178 -0.544035 0.015191 \( \big| 1\sigma_g\alpha 1\sigma_g \beta\big|\) 0.99695 0.00000 0.00000 0.07802 \( \big| 1\sigma_g\beta 1\sigma_u\alpha\big| \) 0.00000 0.70711 0.70711 0.00000 \( \big| 1\sigma_g\alpha 1\sigma_u\beta \big|\) 0.00000 0.70711 -0.70711 0.00000 \( \big| \sigma_u\alpha 1\sigma_u\beta\big| \) -0.07802 0.00000 0.00000 0.99695
Esto muestra, como era de esperar, la mezcla de los primeros\( ^1\sum_g + (1\sigma_g^2 \text{ and the 2nd } ^1\sum_g^+ (1\sigma_u^2 )\) determinantes, el
\[ ^3\sum\limits_u^+ = \left( \dfrac{1}{\sqrt{2}}\left( \big| 1\sigma_g\beta 1\sigma_u\alpha \big| + \big| 1\sigma_g\alpha 1\sigma_u\beta \big| \right) \right) , \]
\[ \text{and the } ^1\sum\limits_u^+ = \left( \dfrac{1}{\sqrt{2}}\left( \big| 1\sigma_g\beta 1\sigma_u\alpha\big| - \big| 1\sigma_g\alpha 1\sigma_u\beta\big|\right) \right) . \]
También observe que el\( ^1\sum\limits_g^+\) estado es el enlace (0 .99695 - 0.07802) (nótese específicamente la combinación + -) y el segundo\(^1\sum\limits_g^+\) estado es la combinación antiadhesión (observe específicamente la combinación + +). La combinación + + siempre da una energía mayor que la combinación + -. También observe que los estados primero y segundo\( (^1\sum\limits_g^+ \text{ and } ^3\sum\limits_u^+ )\) se están disociando a combinaciones de protón/anión. La diferencia en estas energías es el potencial de ionización de H menos la afinidad electrónica de H.
- El resultado de\(H_2\) CI”
-


