2.1: Un contraste de la vieja y la nueva física
- Page ID
- 69387
Considera un electrón de masa m = 9 '10 -28 g el cual está confinado para moverse sobre una línea L cm de longitud. L se establece igual al diámetro aproximado de un átomo, 1 '10 -8 cm = 1Å. Considera también un sistema compuesto por una masa de 1 g confinada para moverse en una línea, digamos de 1 metro de longitud. Aplicaremos la mecánica cuántica al primero de estos sistemas y la mecánica clásica al segundo.
Energía
A medida que cualquiera de las masas se mueve de un extremo de su línea al otro, la energía potencial (la energía que depende de la posición de la masa) permanece constante. Podemos establecer la energía potencial igual a cero, y toda la energía es entonces energía cinética (energía del movimiento). Cuando el electrón llegue al final de la línea, asumiremos que es reflejado por alguna fuerza. Así, en los extremos de la línea la energía potencial se eleva abruptamente a un valor muy grande, tan grande que el electrón nunca podrá “abrirse paso”. Podemos trazar energía potencial versus posición x a lo largo de la línea Fig. 2-1.
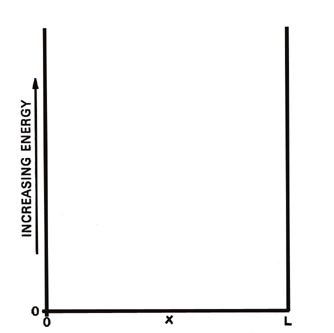 |
Fig. 2-1. Diagrama de energía potencial para una partícula que se mueve sobre una línea de longitud L. Cuando el electrón está en x = 0 o x = L la energía potencial es infinita y para valores de x entre estos límites (0< x < L) la energía potencial es cero. |
Nos referimos al electrón (o la partícula de m = 1 g) como estar en un pozo potencial y podemos imaginar que el potencial abruptamente ascendente en x = 0 y x = L es el resultado de colocar una “pared” en cada extremo de la línea. Primero, ¿cuáles son las predicciones de la mecánica clásica respecto a la energía de la masa de 1 g? La energía total es energía cinética y es simplemente:
|
|
Sabemos por experiencia que u, la velocidad, puede tener cualquier valor posible desde cero hasta valores muy grandes. Dado que todos los valores para u están permitidos, todos los valores para E están permitidos. Concluimos que la energía de un sistema clásico puede tener cualquiera de un rango continuo de valores y puede ser cambiada por cualquier cantidad arbitraria. Contrastemos con esta conclusión la predicción que hace la mecánica cuántica respecto a la energía de un electrón en una situación correspondiente.
Los resultados mecánicos cuánticos son notables, aunque no deberían sorprendernos cuando recordamos la explicación de Bohr de los espectros de líneas que se observan para los átomos. La mecánica cuántica predice que solo hay ciertos valores de la energía que el electrón confinado para moverse en la línea puede poseer. Se cuantifica la energía del electrón. Si se pudiera observar este resultado para una partícula masiva, significaría que solo eran posibles ciertas velocidades, digamos u = 1 cm/s o 10 cm/s ¡pero sin valores intermedios! Pero entonces un electrón no es realmente una partícula. La expresión de las energías permitidas dada por la mecánica cuántica para este sencillo sistema es:
| (1) |
|
|
donde de nuevo h es la constante de Planck y n es un número entero que puede asumir cualquier valor de uno a infinito. Dado que solo son posibles valores discretos para E, es necesaria la aparición del índice n en la ecuación (1). Un número como n que aparece en la expresión de la energía se llama número cuántico. Cada valor del número cuántico n fija un valor de E n, uno de los valores de energía permitidos. Podemos indicar los posibles valores para la energía en un diagrama de energía. Es claro a partir de la ecuación (1) que para valores dados de m y L, E n es igual a una constante (K = h 2 /8mL 2) multiplicada por n 2:
| (2) |
|
|
Así podemos expresar el valor de E n en términos de tantas unidades de K.
Cada línea, llamada nivel de energía, en la Fig. 2-2 denota una energía permitida para el sistema y la figura se denomina diagrama de nivel de energía. Cada nivel se identifica por su valor de n como subíndice. Un diagrama correspondiente para el caso de la partícula clásica consistiría en un número infinito de líneas con espaciamientos infinitesimalmente pequeños entre ellas, indicando que la energía en un sistema clásico puede variar de manera continua y puede asumir cualquier valor. El continuo energético de la mecánica clásica es reemplazado por un conjunto discreto de niveles de energía en la mecánica cuántica.
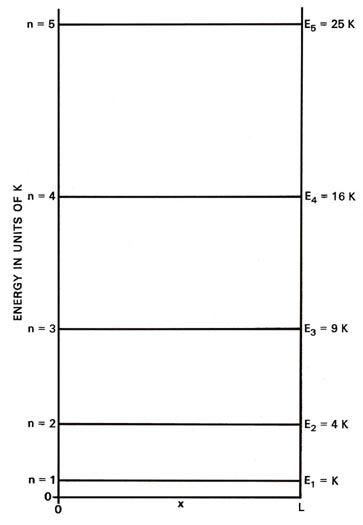 |
Fig. 2-2. Diagrama de nivel de energía para un electrón que se mueve en una línea de longitud L. Solo se muestran los primeros niveles. |
Supongamos que podríamos darle al electrón suficiente energía para colocarlo en uno de los niveles de energía más altos (excitados). Entonces cuando “cayó” de nuevo al valor más bajo de E (llamado nivel del suelo, E 1), se emitiría un fotón. La energía e del fotón estaría dada por la diferencia en los valores de E n y E 1 y, ya que e = hv la frecuencia del fotón estaría dada por la relación:
|
|
|
que es la condición de frecuencia de Bohr (I-4). Así solo se emitirían ciertas frecuencias y el espectro consistiría en una serie de líneas.
Podemos ilustrar el cambio en la energía cuando el electrón cae al nivel de energía más bajo conectando el nivel superior y el nivel n = 1 por una flecha en un diagrama de nivel de energía. La frecuencia del fotón emitido durante la caída de energía indicada es proporcional a la longitud de la flecha, es decir, al cambio de energía (Fig. 2-3). La línea directamente debajo de cada flecha representa el valor de la frecuencia para esa caída de energía. Dado que las diferencias en las longitudes de las flechas aumentan a medida que n aumenta, las separaciones entre las frecuencias observadas muestran un incremento correspondiente. El espectro, por lo tanto, consiste en una serie de líneas, con los espaciamientos entre las líneas aumentando a medida que n aumenta. Si no se cuantificara la energía y todos los valores fueran posibles, todos los saltos de energía serían posibles y aparecerían todas las frecuencias. Así, un continuo de posibles valores de energía producirá un espectro continuo de frecuencias. Un espectro lineal, por otro lado, es una manifestación directa de la cuantificación de la energía.
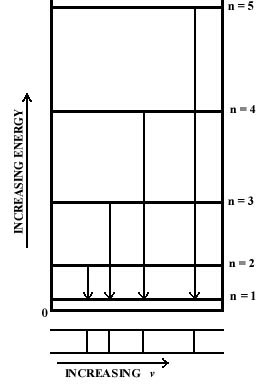 |
Fig. 2-3. El origen de los espectros de una línea. |
En el caso cuántico, como en el caso clásico, toda la energía estará en forma de energía cinética. Podemos obtener una expresión para el impulso del electrón igualando el valor total de la energía E n a p 2 /2m, donde p es el impulso
(= m u) del electrón, ( p 2 /2m es otra forma de expresar 2 m u 2.)
|
|
Esto da:
|
|
|
Se debe colocar un signo más y un signo menos frente al número lo que da la magnitud del impulso para indicar que no sabemos y no podemos determinar la dirección del movimiento. Si el electrón se mueve de izquierda a derecha el signo será positivo. Si se mueve de derecha a izquierda el signo será negativo. Lo máximo que podemos saber sobre el impulso en sí es su valor promedio. Este valor será claramente cero debido a la igual probabilidad de movimiento en cualquier dirección. El valor promedio de p 2, sin embargo, es finito.
Dado que el valor más bajo permitido del número cuántico n en la expresión mecánica cuántica para la energía es la unidad, es evidente que la energía nunca puede ser igual a cero. Un electrón confinado nunca puede estar inmóvil. La expresión para E n también indica que la energía cinética y el impulso aumentan a medida que disminuye la longitud de la línea L. Así, la energía cinética y el impulso del electrón aumentan a medida que su movimiento se vuelve más confinado. Este es a la vez un resultado importante y general y se volverá a referir.
Posición
El concepto de trayectoria es fundamental para la mecánica clásica. Dada una masa particular con una velocidad inicial dada y un conocimiento de las fuerzas que actúan sobre ella, podemos usar la mecánica clásica para predecir la posición exacta y la velocidad de la partícula en cualquier momento futuro. Así hablamos de la trayectoria de la partícula y podemos calcularla con cualquier grado de precisión que se desee. También es posible, dentro del marco de la mecánica clásica, medir la posición y velocidad de una partícula en cualquier instante de tiempo dado. Así, la mecánica clásica predice correctamente lo que se puede medir experimentalmente para partículas masivas.
Anteriormente hemos mencionado las dificultades que se encuentran cuando intentamos determinar la posición de un electrón. Los resultados del efecto Compton indican que parte de la energía del fotón utilizada en la realización de la observación se transfiere al electrón, e invariablemente perturbaremos al electrón cuando intentamos medir su posición. Por lo tanto, no es sorprendente encontrar que la mecánica cuántica no predice exactamente la posición de un electrón. Más bien, proporciona solo una probabilidad en cuanto a dónde se encontrará el electrón. Al considerar los experimentos que intentan definir la posición del electrón, encontraremos que esta es la información máxima que efectivamente se puede obtener incluso experimentalmente. La nueva mecánica nuevamente predice solo lo que efectivamente se puede medir experimentalmente. Ilustraremos el aspecto de probabilidad en términos del sistema de un electrón confinado al movimiento a lo largo de una línea de longitud L. Las probabilidades mecánicas cuánticas se expresan en términos de una función de distribución que en este caso particular etiquetaremos P n (x).
Considera que la línea de longitud L se divide en un gran número de segmentos muy pequeños, cada uno de longitud D x. Entonces la probabilidad de que el electrón esté en un segmento pequeño particular D x de la línea viene dada por el producto de D x y el valor de la función de distribución de probabilidad P n (x) para ese intervalo. Por ejemplo, la función de distribución de probabilidad para el electrón cuando está en el nivel de energía más bajo, n = 1, viene dada por P 1 (x) (Fig. 2-4).
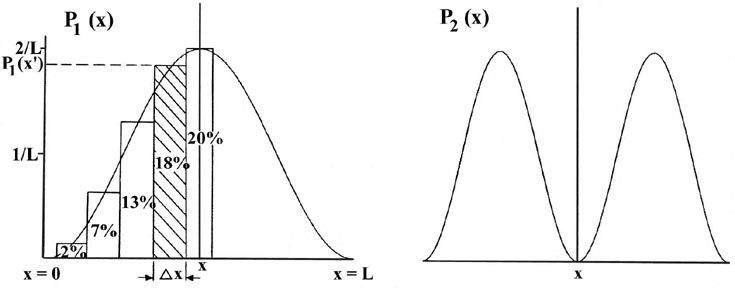
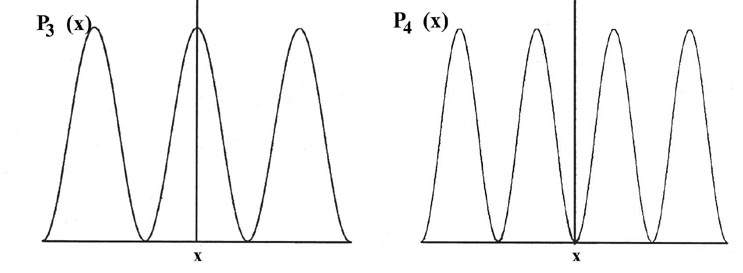
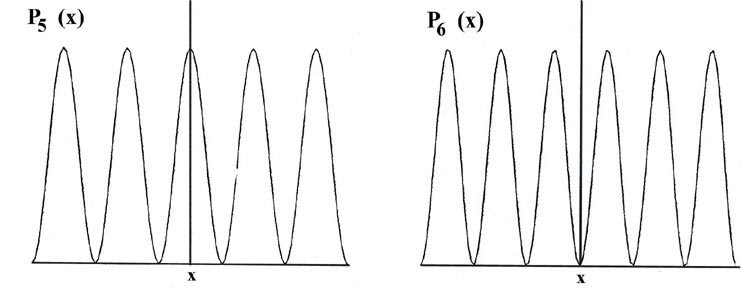
Fig. 2-4. Distribuciones de probabilidad P n (x) para un electrón confinado para moverse en una línea de longitud fija en los niveles cuánticos con n = 1, 2,..., 6. El área de cada rectángulo que se muestra en la figura para P 1 (x) es igual a la probabilidad de que el electrón esté en el segmento particular de la línea D x formando la base del rectángulo. El porcentaje que se muestra en cada rectángulo es el porcentaje de probabilidad de que el electrón esté en un segmento particular D x. La probabilidad total de que el electrón esté en algún lugar de la línea viene dada por el área total bajo la curva P 1 (x), es decir, por la suma de cada pequeño elemento del área P 1 (x) D x por cada segmento D x. Esta área total se hace igual a la unidad por cada curva de P n (x) expresando los valores de P n (x) en unidades de (1/L). Así, por definición, una probabilidad de uno denota una certeza.
La probabilidad de que el electrón esté en el intervalo pequeño particular D x indicado en la Fig. 2-4 es igual al área sombreada, área que a su vez es igual al producto de D x y al valor promedio de P 1 (x) a lo largo del intervalo D x, llamado P 1 (x '),
|
|
La curva P1 (x) se puede determinar de la siguiente manera. Diseñamos un experimento capaz de determinar si el electrón se encuentra o no en un segmento particular D x de la línea cuando se sabe que está en el nivel cuántico n = 1. (Una forma en la que esto podría hacerse se describe a continuación.) Realizamos el experimento un gran número de veces, digamos cien, por cada segmento y registramos la relación entre el número de veces que el electrón se encuentra en un segmento en particular y el número total de observaciones realizadas para ese segmento. Por ejemplo, se encuentra que un electrón está en el segmento marcado D x (de longitud 0.1 L) en la figura para P 1 (x) en 18 de cada 100 observaciones, o 18% del tiempo. En las otras 82 observaciones el electrón estaba en uno de los otros segmentos. Así, el valor promedio de P 1 (x) para este segmento, llamado P 1 (x ') debe ser 1.8/ L ya que P 1 (x') D x = (1.8/ L) (0.1 L) = 0.18 o 18%. Se realiza un conjunto similar de experimentos para cada uno de los segmentos D x y en cada caso se construye un rectángulo con D x como base y con una altura igual a P 1 (x) tal que el producto P 1 (x) D x es igual al número fraccional de veces que el electrón se encuentra en el segmento D x. El caso limitante en el que la longitud total L se divide en un número muy grande de segmentos muy pequeños (D x ® d x) daría como resultado la curva suave que se muestra en la figura para P 1 (x).
Existe una distribución de probabilidad diferente para cada valor de E n, o cada nivel cuántico, como se muestra, por ejemplo, por las distribuciones de probabilidad para los niveles de energía con n = 2, 3, 4, 5 y 6 (Fig. 2-4). La probabilidad de encontrar el electrón en las posiciones donde la curva toca el eje x es cero. Tal cero se denomina nodo. El número de nodos siempre es n -1 si no contamos los nodos en los extremos de cada curva P n (x).
Primero contrastemos estos resultados, particularmente el de P 1 (x), con el caso clásico correspondiente. Dado que un análisis clásico nos permite determinar la posición de una partícula de manera única en cualquier instante, ya sea teórica o experimentalmente, la idea de una distribución de probabilidad es ajena a un análisis mecánico clásico. Sin embargo, todavía podemos determinar la distribución de probabilidad clásica para la partícula confinada al movimiento en una línea. Dado que no hay fuerzas que actúen sobre la partícula a medida que atraviesa la línea, será igualmente probable que se encuentre en cualquier punto de la línea (Fig 2-5). Esta probabilidad será la misma independientemente de la energía. De nuevo hay una diferencia notable entre los resultados de la mecánica clásica y cuántica. Para el primer nivel cuántico, la gráfica de P 1 (x) indica que lo más probable es que el electrón se encuentre en el punto medio de la línea. Además, la forma de P n (x) cambia con cada cambio en la energía. Cada valor permitido del de la energía ha asociado con él una distribución de probabilidad distinta para el electrón. Estas son las predicciones de la mecánica cuántica respecto a la posición de un electrón unido. Ahora investiguemos el aspecto experimental del problema para obtener alguna razón física para estas predicciones.
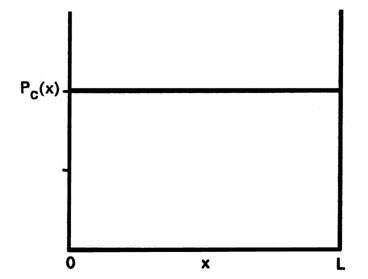 |
Fig. 2-5. La distribución de probabilidad clásica para el movimiento en una línea. Este es el resultado que se obtiene cuando la partícula se localiza un gran número de veces a intervalos de tiempo aleatorios. La función de probabilidad clásica P c (x) es la misma para todos los valores de x e igual a 1/ L, es decir, es igualmente probable que la partícula se encuentre en cualquier valor de x entre 0 y L |
Diseñemos un experimento en el que intentemos identificar la posición de un electrón dentro de un segmento D x. El experimento es hipotético en el sentido de que imaginamos que debemos observar el electrón a través de un microscopio reflejando o dispersando la luz del mismo. Imagine que la lente de un microscopio se coloca por encima de la línea L con la luz entrando desde un lado (Fig. 2-6 (a)). El electrón, cuando se ilumina con luz, actuará como una pequeña fuente de luz y producirá en A una imagen en forma de disco brillante rodeado por un grupo de anillos de intensidad decreciente. Debido a este efecto, que es totalmente análogo al efecto de difracción observado para una fuente de luz estenopeica, el centro de la imagen aparecerá brillante incluso si el electrón no se localiza con precisión en el punto marcado x. Igualmente bien podría haber estado en cualquier valor de x entre los puntos x 'y x "y producir una imagen visible para el ojo en A si la diferencia en las longitudes de ruta B x' y C x '(o B x" y C x “) es menos de la mitad de una longitud de onda. En otras palabras, el poder de resolución de un microscopio no es ilimitado sino que está determinado por la longitud de onda de la luz utilizada para realizar la observación. El uso del microscopio impone una incertidumbre inherente en nuestra observación de la posición del electrón. Con la condición de que la diferencia en las longitudes de trayectoria al borde exterior de la lente no debe ser mayor de media longitud de onda y con el uso de alguna geometría, la magnitud de la incertidumbre en la posición del electrón, x "- x '= D x, es que se encuentran dadas aproximadamente por:
| (3) |
|
donde q es el ángulo indicado en el diagrama.
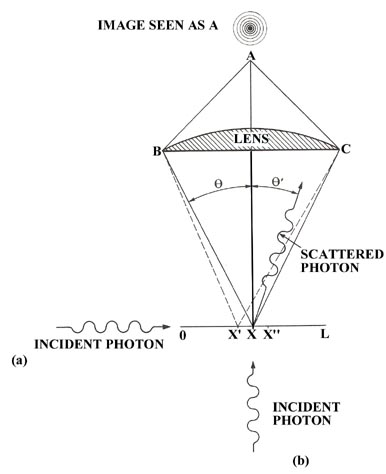
Fig. 2-6. Un experimento idealizado para detectar la posición de un electrón.
Recordando el efecto Compton y teniendo en cuenta que deseamos perturbar el electrón lo menos posible durante la observación, indagaremos en cuanto a los resultados obtenidos cuando un solo fotón se dispersa del electrón. Un solo fotón no producirá el patrón de difracción completo en A, sino que producirá un solo destello de luz. Un patrón de difracción es el resultado de muchos fotones que pasan por el microscopio y representa la distribución de probabilidad para los fotones emergentes cuando han sido dispersados por un electrón que se encuentra entre x 'y x”. Sin embargo, un solo fotón, cuando se dispersa desde un electrón dentro de la longitud D x, todavía se difracta y producirá un destello de luz en alguna parte de una de las áreas definidas por la distribución de probabilidad producida por muchos fotones que pasan por el sistema.
Así, incluso cuando usamos un solo fotón en nuestro aparato, la incertidumbre D x en nuestra posición determinada experimentalmente del electrón seguirá estando dada por la ecuación (3). Obviamente, si queremos localizar un electrón que está confinado para moverse en una línea hasta dentro de una longitud que es pequeña en comparación con la longitud de la línea, debemos usar luz que tiene una longitud de onda mucho menor que L. Esto es exactamente lo que establece la ecuación (3): cuanto más corta sea la longitud de onda de la luz que se utiliza para observar el electrón, menor será la incertidumbre D x. Siendo ese el caso, ¿por qué no hacer el experimento con luz de longitud de onda muy corta comparado con la longitud L, digamos l = (1/100) L? Entonces podemos esperar encontrar el electrón en un pequeño segmento de la línea, siendo cada segmento aproximadamente (1/100) L de longitud. Calculemos la frecuencia y energía de un fotón que tiene la longitud de onda requerida de l = (1/100) L. Como antes, establecemos L igual a una dimensión atómica típica de 1 x 10 -8 cm.
|
|
Estamos inmediatamente en dificultad, porque la energía del electrón en el primer nivel cuántico se encuentra fácilmente como:
|
|
¡La energía del fotón es aproximadamente 1 x 10 4 veces mayor que la energía del electrón! Sabemos por el efecto Compton que la colisión de un fotón con un electrón imparte energía al electrón. Por lo tanto, el electrón después de la colisión ciertamente no estará en el estado n = 1. Estará excitado a una C no sabemos cuál C de los niveles excitados con n = 2 (E = 4 K) o n = 3 (E = 9 K), etc. el resultado es claro. Si exigimos un conocimiento íntimo de cuál es la posición del electrón en un estado dado, podemos obtener esta información solo a expensas de impartir al electrón una cantidad desconocida de energía que destruye el sistema, es decir, el electrón ya no está en el nivel n = 1 sino en uno de los otros niveles excitados. Si este experimento se repitiera un gran número de veces y se mantuviera un registro del número de veces que se localizó un electrón en cada segmento de la línea (aproximadamente (1/100) L), se obtendría una gráfica de probabilidad similar a la Fig. 2-4.
Podemos hacer otro tipo de pregunta respecto a la posición del electrón: “¿Cuánta información se puede obtener sobre la posición del electrón en un nivel cuántico dado sin destruir al mismo tiempo ese nivel?” El electrón no puede aceptar energía en una cantidad menor a la necesaria para excitarla al siguiente nivel cuántico, n = 2. La diferencia de energía entre E 2, y E 1, es de 3 K. Así, si vamos a dejar al electrón en un estado de energía e impulso conocidos debemos utilizar la luz cuyos fotones posean una energía inferior a 3 K.
Calculemos la longitud de onda de la luz con e = 2 K y comparemos este valor con la longitud L.
|
|
La longitud de onda es mayor que la longitud de la línea L. De la ecuación (3) queda claro que la incertidumbre en la posición de la partícula será del orden de magnitud de, o mayor que, L misma. ¡El electrón parecerá estar borroso en toda la longitud de la línea en un solo experimento! Así, hay dos interpretaciones que se pueden dar a las distribuciones de probabilidad, dependiendo del experimento que se realice. El primero es el de una verdadera probabilidad de encontrar el electrón en un segmento pequeño dado de la línea usando luz de l muy corta con relación a L. Este experimento excita al electrón, cambia el sistema y deja el electrón con una cantidad desconocida de energía e impulso. Hemos destruido el objeto de nuestra investigación. Ahora sabemos dónde estaba en un experimento dado pero no dónde estará, en términos de energía o posición.
Alternativamente, podríamos usar luz con una l aproximadamente igual a L. Esto no excita al electrón y lo deja en un nivel de energía conocido. No obstante, ahora el conocimiento de la posición es muy incierto. Los fotones están dispersos del sistema y nos dan directamente la distribución manchada P 1 que se muestra en la Fig. 2-4. En un sentido real debemos aceptar el hecho de que cuando el electrón permanece en un estado dado se “mancha” y “se parece” a las imágenes dadas para P n. Así podemos interpretar los Pn's como imágenes instantáneas del electrón cuando está atado en un estado conocido, y olvidamos su aspecto de probabilidad. A esta distribución “manchada” se le da un nombre especial; se llama distribución de densidad electrónica. Habrá una cierta fracción de la carga electrónica total en cada punto de la línea, y cuando consideremos un sistema en tres dimensiones, habrá una cierta fracción de la carga electrónica total en cada pequeño volumen de espacio. De ahí que se le dé el nombre densidad electrónica, la cantidad de carga por unidad de volumen de espacio. Los P n representan una distribución de densidad de carga que se considera estática siempre y cuando el electrón permanezca en el n º nivel cuántico. Así las funciones P n nos dicen o bien (a) la fracción de tiempo que el electrón está en cada punto de la línea para observaciones que emplean luz de longitud de onda corta, o (b) nos dicen la fracción de la carga total que se encuentran en cada punto de la línea (la totalidad de la carga se extiende) cuando las observaciones se realizan con luz de longitud de onda relativamente larga.
Las distribuciones de densidad electrónica de átomos, moléculas o iones en un cristal pueden determinarse experimentalmente mediante experimentos de dispersión de rayos X ya que los rayos X pueden generarse con longitudes de onda del mismo orden de magnitud que los diámetros atómicos (1 '10 -8 cm). En la dispersión de rayos X se mide la intensidad del haz disperso y el ángulo a través del cual se dispersa. La distribución de carga negativa dentro del cristal dispersa los rayos X y determina la intensidad y el ángulo de dispersión. Así, estas cantidades experimentales pueden ser utilizadas para calcular la forma de la distribución de la densidad electrónica.
Existe una relación mecánica cuántica definida que rige las magnitudes de las incertidumbres encontradas en las mediciones a nivel atómico. Podemos ilustrar esta relación para el sistema unidimensional. Consideremos la mínima incertidumbre en nuestras observaciones de la posición y el impulso del electrón que se mueve sobre una línea obtenida en un experimento que deja la partícula unida en un nivel cuántico dado, digamos n = 1. Esto requerirá el uso de luz con l ~ L. Hemos visto que el uso de la luz de esta longitud de onda nos limita a afirmar que el electrón está en algún lugar de la línea de longitud L. No podemos decir más que esto con certeza a menos que usemos luz de l mucho más corta, y luego cambiaremos el número cuántico del electrón. La incertidumbre en el valor de la coordenada de posición, que llamaremos D x, es solo L, la longitud de la línea:
|
|
Anteriormente hemos demostrado que el impulso del electrón en el enésimo nivel cuántico viene dado por:
|
|
|
los signos más y menos que denotan el hecho de que si bien conocemos la magnitud del impulso no podemos determinar si el electrón se mueve de izquierda a derecha (+ nh /2 L) o de derecha a izquierda (- nh /2 L). La incertidumbre mínima en nuestro conocimiento del impulso es la diferencia entre estas dos posibilidades, o para n = 1:
|
|
El producto de las incertidumbres en la posición y el impulso es:
|
|
Este resultado es un ejemplo particular de una relación general que rige el producto de las incertidumbres en el impulso y la posición conocida como principio de incertidumbre de Heisenberg. En el caso general, el signo de igualdad en la ecuación anterior se sustituye por el símbolo "³" que denota que el producto en las incertidumbres D p D x es igual o superior al valor del contant h de Planck, es decir, la declaración general viene dada por D p D x ³ h.
Si nos esforzamos por disminuir la incertidumbre en la coordenada de posición (es decir, hacer D x pequeña) habrá un incremento correspondiente en la incertidumbre del impulso del electrón a lo largo de la misma coordenada, de tal manera que el producto de las dos incertidumbres siempre es igual al de Planck constante. Vimos este efecto en nuestros experimentos en los que empleamos luz de l corto para localizar la posición del electrón con mayor precisión. Cuando hicimos esto excitamos el electrón a uno de los otros estados cuánticos disponibles, haciendo así un conocimiento de la energía y de ahí el impulso incierto. También podríamos tratar de derrotar el principio de incertidumbre de Heisenberg disminuyendo la longitud de la línea L. Al acortar L, disminuiríamos la incertidumbre en cuanto a dónde está el electrón. Sin embargo, como se señaló anteriormente, el impulso aumenta a medida que L disminuye y la incertidumbre en p es siempre del mismo orden de magnitud que la p misma; en este caso el doble de la magnitud de p. Así, la disminución en D x obtenida por la disminución de L se compensa con el incremento en D p que acompaña al aumento de confinamiento del electrón; el producto D x D p permanece sin cambios en valor.
Podemos ilustrar el funcionamiento del principio de incertidumbre de Heisenberg para una partícula libre haciendo referencia nuevamente a nuestro hipotético experimento en el que intentamos localizar la posición de un electrón usando un microscopio. Imaginamos que el electrón está libre y viajando con un impulso conocido en la dirección del eje x con un fotón entrando desde abajo a lo largo del eje y. Cuando el fotón es dispersado por el electrón puede transferir impulso al electrón y continuar en una línea que forma un ángulo q 'con respecto al eje y (Fig. 2-6). El fotón, al hacerlo, adquirirá impulso en la dirección del eje x, dirección en la que inicialmente no tuvo ninguno. Dado que el impulso debe conservarse, el electrón recibirá un impulso de retroceso, un impulso igual en magnitud pero opuesto en dirección al ganado por el fotón. Este es el efecto Compton. Así, nuestro acto de observar el electrón conducirá a una incertidumbre en su impulso ya que la cantidad de impulso transferida durante la colisión es incontrolable. Podemos, sin embargo, establecer límites sobre la cantidad transferida y de esta manera determinar la incertidumbre introducida en el valor del impulso del electrón.
El impulso del fotón antes de la colisión se dirige a lo largo del eje y y tiene una magnitud igual a h/l. Después de chocar con el electrón el fotón puede ser dispersado a la izquierda o a la derecha del eje y a través de cualquier ángulo q 'que se encuentre entre 0 y q y aún así ser recogido por la lente del microscopio y visto por el observador en A. Así, cada fotón que pase por el microscopio tendrá una incertidumbre de 2 (h/l) sin q en su componente de impulso a lo largo del eje x ya que puede haber sido dispersado por la cantidad máxima hacia la izquierda y adquirido un componente de - (h/l) sin q o, por otro lado, pudo haber sido dispersado por la cantidad máxima hacia la derecha y adquirido un componente de impulso de + (h/l) sin q. Cualquier componente x del impulso adquirido por el fotón debe haber sido perdido por el electrón y la incertidumbre introducida en el momento del electrón por la observación también es igual a 2 (h/l) sin q.
Además de la incertidumbre inducida en el momento del electrón por el acto de medición, también existe una incertidumbre inherente en su posición (ecuación (3)) debido al limitado poder de resolución del microscopio. El producto de las dos incertidumbres en el instante de la medición o inmediatamente después de ella es:
|
|
La relación de incertidumbre de Heisenberg vuelve a cumplirse. Nuestro experimento emplea sólo un único fotón que, dado que la luz misma está cuantificada, representa el paquete más pequeño de energía e impulso que podemos utilizar para hacer la observación. Incluso en este experimento idealizado el acto de observación crea una perturbación inevitable en el sistema.
Degeneración
Podemos usar una extensión de nuestro sistema simple para ilustrar otro resultado mecánico cuántico importante con respecto a los niveles de energía. Supongamos que permitimos que el electrón se mueva en el plano x -y en lugar de solo a lo largo del eje x. Los movimientos a lo largo de las direcciones x e y serán independientes entre sí y la energía total del sistema vendrá dada por la suma del cuántico de energía para el movimiento a lo largo del eje x más el cuántico de energía para el movimiento a lo largo del eje y. Ahora serán necesarios dos números cuánticos, uno para indicar la cantidad de energía a lo largo de cada coordenada. Los etiquetaremos como n x y n y. Supongamos que el movimiento se limita a una longitud L a lo largo de cada eje, entonces:
|
|
|
No se encuentra nada nuevo cuando el electrón se encuentra en el nivel cuántico más bajo para el cual n x = n y = 1. La energía E 1,1 simplemente equivale a 2 h 2 /8 mL 2.
Dado que ahora se requieren dos dimensiones (x e y) para especificar la posición del electrón, la distribución de probabilidad P 1,1 (x, y) debe trazarse en la tercera dimensión. Sin embargo, podemos mostrar P 1,1 (x, y) en un diagrama bidimensional en forma de mapa de contorno (Fig. 2-7). Todos los puntos en el plano x -y que tienen el mismo valor para la distribución de probabilidad P 1,1 (x, y) están unidos por una línea, una línea de contorno. Los valores de los contornos aumentan de lo más externo al más interno, y el electrón, cuando está en el nivel n x = n y = 1, es por lo tanto más probable que se encuentre en la región central de la x -y avión.
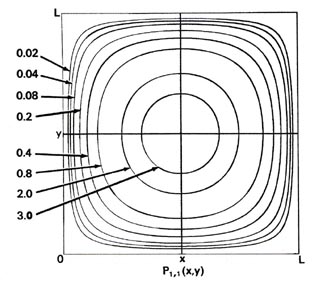
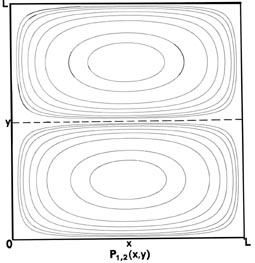
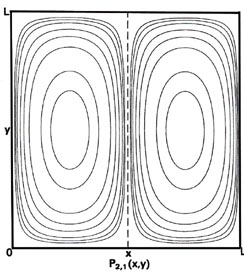

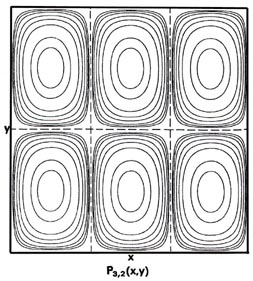
Fig. 2-7. Mapas de contorno de las distribuciones de probabilidad P n x, n y (x, y) para un electrón que se mueve en el plano x-y. Las líneas discontinuas representan la posición de nodos, líneas a lo largo de las cuales la probabilidad es cero. P 1,2 (x, y) y P 2,1 (x, y) son distribuciones para un nivel doblemente degenerado; P 2,3 (x, y) y P 3, 2 (x, y) son ejemplos de distribuciones para otro nivel degenerado de energía aún mayor. Se muestran los mismos contornos en cada diagrama y sus valores (en unidades de 4/ L 2) se indican en el diagrama para P 1,1 (x, y).
Una gráfica de P 1,1 (x, y) a lo largo de cualquiera de los ejes indicados en la Fig. 2-7 (uno paralelo al eje x en y = L/2 y el otro paralelo al eje y en x = L/2) es similar en apariencia a la para P 1 (x) que se muestra en la Fig. 2-4. Es decir, para un valor fijo de y, la contribución a P 1,1 (x, y) del movimiento a lo largo del eje y es constante y
|
|
Así, aparte del factor constante, P 1 (x) proporciona un perfil, o si P 1,1 (x, y) se visualizaron en tres dimensiones, una sección transversal del mapa de contorno de P 1,1 (x). Un mapa de contorno es una visualización de la distribución de probabilidad o densidad en un plano; un perfil es una visualización de la distribución de densidad a lo largo de una línea.
Ahora considere la posibilidad de n x = 1 y n y = 2. Entonces
|
|
También podríamos tener la situación en la que n x = 2 y n y = 1. Esto no cambia el valor de la energía total,
|
|
pero las distribuciones de probabilidad (Fig. 2-7) son diferentes, P 1,1 (x, y) ¹ P 2,1 (x, y). Cuando n x = 1 y n y = 2, debe haber un nodo en el eje y, es decir, una probabilidad cero de encontrar el electrón en y = L/2. Así, un corte a través de P 1,2 (x y) en x = L/2 paralelo al eje y debe ser similar a la figura para P 2 (x), mientras que un corte paralelo al eje x sigue siendo similar a P 1 (x). Solo lo contrario es cierto para el caso n x = 2 y n y = 1. En este caso, independientemente de que podamos distinguir o no experimentalmente entre los ejes x - e y, existen dos arreglos diferentes para la distribución del electrón, los cuales tienen la misma energía. Se dice que el nivel de energía es degenerado. La degeneración de un nivel de energía es igual al número de distribución de probabilidad distinta para el sistema, todos los cuales pertenecen a este mismo nivel de energía.
El concepto de degeneración en un nivel de energía tiene importantes consecuencias en nuestro estudio de la estructura electrónica de los átomos.

