1.13: Espectroscopia Molecular

Nuestro conocimiento más detallado de la estructura atómica y molecular se ha obtenido a partir de espectroscopia-estudio de la emisión, absorción y dispersión de radiación electromagnética acompañando transiciones entre niveles de energía atómica o molecular. Mientras que los espectros atómicos involucran solo transiciones electrónicas, la espectroscopia de moléculas es más intrincada porque los grados de libertad vibracional y rotacional también entran en juego. Las primeras observaciones de absorción o emisión por moléculas se caracterizaron como espectros de banda en contraste con los espectros lineales exhibidos por los átomos. Ahora se entiende que estas bandas reflejan energías vibracionales y rotacionales muy espaciadas aumentando los estados electrónicos de una molécula. Con mejoras en las técnicas espectroscópicas a lo largo de los años, se ha hecho posible resolver transiciones vibracionales y rotacionales individuales. Esto ha proporcionado una rica fuente de información sobre geometría molecular, energética y dinámica. La espectroscopia molecular también ha contribuido significativamente a la química analítica, la ciencia ambiental, la astrofísica, la biofísica y la bioquímica.

Masa Reducida

Considerar un sistema de dos partículas de masas\(m_1\) e\(m_2\) interactuar con una energía potencial que depende únicamente de la separación de las partículas. La energía clásica viene dada por\[E=\frac{1}{2} m_1 \dot{\vec{r}}_1^2+\frac{1}{2} m_2 \dot{\vec{r}}_2^2+V (|\vec{r}_2-\vec{r}_1|) \label{1}\] los puntos que significan tiempo wrt derivado. Introducir dos nuevas variables, la separación de partículas\(\vec{r}\) y la posición del centro de masa\(\vec{R}\):

\[ \vec{r}=\vec{r}_2-\vec{r}_1 \mbox{,}\hspace{20pt}\vec{R}=\dfrac{m_1 \vec{r}_1+m_2\vec{r}_2}{m}\label{2}\]

donde\(m=m_1+m_2\). En cuanto a las nuevas coordenadas

\[\vec{r}_1=\vec{R}+\frac{m_2}{m} \vec{r} \mbox{,}\hspace{20pt}\vec{r}_2=\vec{R}-\frac{m_1}{m} \vec{r}\label{3}\]

y

\[E=\dfrac{1}{2}m\dot{\vec{R}}^2+\dfrac{1}{2}\mu\dot{\vec{r}}^2+V(r)\label{4}\]

donde\(r=|\vec{r}|\) y\(\mu\) se llama\(reduced\hspace{2pt}mass\)

\[\mu\equiv\dfrac{m_1 m_2}{m_1+m_2}\label{5}\]

Una relación alternativa para la masa reducida es

\[\dfrac{1}{\mu}=\frac{1}{m_1}+\frac{1}{m_2}\label{6}\]

que recuerda a la fórmula de resistencia de un circuito paralelo. Tenga en cuenta que, si\(m_2\rightarrow\infty\), entonces\(\mu\rightarrow m_1\). El término que contiene\(\dot{\vec{R}}\) representa la energía cinética de una sola partícula hipotética de masa\(\mu\) localizada en el centro de masa\(\vec{R}\). Los términos restantes representan el\(relative\) movimiento de las dos partículas. Fue la aparición de una\(single\) partícula de masa efectiva\(\mu\) moviéndose en el campo potencial\(V(r)\).

\[E_{rel}=\dfrac{1}{2} \mu \dot{\vec{r}^2}+V(r)= \dfrac{\vec{p}^2}{2\mu}+V(r)\label{7}\]

Podemos escribir así la ecuación de Schrödinger para el movimiento relativo

\[ \left\{-\dfrac{\hbar^2}{2 \mu} \bigtriangledown^2+V(r) \right\}\psi (\vec{r})= E \psi (\vec{r}) \label{8}​\]

Cuando tratamos el átomo de hidrógeno, se asumió que la masa nuclear era infinita. En ese caso podemos establecer\(\mu =m\), la masa de un electrón. Se calculó que la constante de Rydberg para la masa nuclear infinita era

\[R_\infty = \dfrac{2\pi^2me^4}{h^3c}=109,737 \text{cm} ^{-1}\label{9}\]

Si en cambio, usamos la masa reducida del sistema electrón-protón

\[\mu = \dfrac{mM}{m+M} \approx \dfrac{1836}{1837}\, m \approx 0.999456 \, m \label{10}\].

Esto cambia la constante de Rydberg para el hidrógeno a

\[R_{H}\approx 109,677 \, cm^{-1}\label{11}\]

en perfecto acuerdo con el experimento.

En 1931, H. C. Urey evaporó cuatro litros de hidrógeno hasta un mililitro y midió el espectro del residuo. El resultado fue un conjunto de líneas desplazadas ligeramente del espectro de hidrógeno. Esto equivalía al descubrimiento del deuterio, o hidrógeno pesado, por lo que Urey fue galardonado en 1934 con el Premio Nobel de Química. Estimando la masa del deuterón, ² H ₁, como el doble de la del protón, da

\[R_{D}\approx 109,707 \, cm^{-1}\label{12}\]

Otro ejemplo interesante que involucra una masa reducida se refiere al positronio, una combinación de corta duración de un electrón y un positrón-la antipartícula del electrón. El electrón y la posición se aniquilan mutuamente con una vida media de aproximadamente 10 ^-7 seg. y el positroio se descompone en rayos gamma. La masa reducida de positronio es

\[ \mu = \frac{m \times m}{m+m} = \frac{m}{2} \label{13} \]

la mitad de la masa del electrón. Así, la energía de ionización equivale a 6.80 eV, la mitad de la del átomo de hidrógeno. La tomografía por emisión de positrones (PET) proporciona una técnica de escaneo sensible para el funcionamiento del tejido vivo, especialmente el cerebro. Se inyecta en el cuerpo un compuesto que contiene un radionúclido emisor de positrones, por ejemplo, ¹¹ C, ¹³ N, ¹⁵ O o ¹⁸ F. Los positrones emitidos se unen a los electrones para formar positronio de corta duración, y se monitorea la radiación de aniquilación.

Vibración de moléculas diatómicas

Una molécula diatómica con masas nucleares M _A, M _B tiene una masa reducida

\[\mu =\frac{M_{A}M_{B}}{M_{A}+M_{B}}\label{14}\]

La solución de la ecuación electrónica de Schrödinger da la energía en función de la distancia internuclear E _elec (R). Esto juega el papel de una función de energía potencial para el movimiento de los núcleos V (R), como se esboza en la Fig. 2. Así podemos escribir la ecuación de Schrödinger para vibración

\ [\ begin {Bmatrix}
-\ frac {\ hbar^2} {2\ mu}\ frac {d^2} {dr^2} +V (R)\ end {Bmatrix}\ chi (R) =E_ {\ chi} (R)\ label {15}\]

Si la energía potencial se expande en una serie de Taylor sobre R = R _e

\[V(R)=V(R_{e})+(R-R_{e})V'(R_{e})+\frac{1}{2}(R-R_{e})^2V"(R_{e})+...\label{16}\]

Una aproximación para esta expansión tiene la forma de un oscilador armónico con

\[V(R)\approx \frac{1}{2}k(R-R_{e})^2\label{17}\]

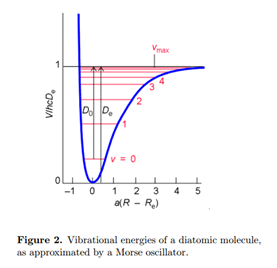
El origen de la energía se puede elegir de manera que V (R _e) = 0. Al mínimo del potencial, V' (R _e) = 0. El mejor ajuste a la parábola (17) se obtiene con un conjunto constante de fuerza igual a

\[k\approx \frac{d^2V(R)}{dR^2}\mid _{R\, =\, R_{e}}\label{18}\]

A partir de la solución para el oscilador armónico, identificamos la energía vibratoria del estado fundamental, con número cuántico\(\nu\) = 0

\[E_{0}=\hbar\omega =\hbar\sqrt{\frac{k}{\mu }}\label{19}\]

La energía de disociación real del estado vibratorio del suelo es entonces aproximada por

\[D_{0}\approx D_{e}-\frac{1}{2}\hbar\omega\label{20}\]

En unidades de número de onda

\[hcD_{0}\approx hcD_{e}-\frac{1}{2}\tilde{\nu }\: cm^{-1}\label{21}\]

Un tratamiento mejorado de la vibración molecular debe dar cuenta de la anharmonía, desviación de un oscilador armónico. La anarmonicidad da como resultado un número finito de niveles de energía vibratoria y la posibilidad de disociación de la molécula a una energía suficientemente alta. Una aproximación muy exitosa para la energía de una molécula diatómica es el potencial Morse:

\[V(R)=hcD_{e}\begin{Bmatrix}1-e^{a(R-R_{e})}\end{Bmatrix}^2\; \; \; a=\begin{pmatrix}\frac{\mu \omega ^2}{2hcD_{e}}\end{pmatrix}^{\frac{1}{2}}\label{22}\]

Obsérvese que V (R _e) = 0 al mínimo del pozo potencial. La ecuación de Schrödinger para un oscilador Morse puede resolver para dar los niveles de energía

\[E_{\upsilon }=(\upsilon +\frac{1}{2})\hbar\omega-(\upsilon+\frac{1}{2} )^2\hbar\omega x_{e}\label{23}\]

o, expresado en unidades de número de onda,

\[hcE_{\upsilon }=(\upsilon +\frac{1}{2})\tilde{\nu }-(\upsilon +\frac{1}{2})^2x_{e}\tilde{\nu }\label{24}\]

Los niveles más altos de energía vibratoria están más cerca entre sí, al igual que en las moléculas reales. Las transiciones vibracionales de las moléculas diatómicas ocurren en el infrarrojo, aproximadamente en el rango de 50-12,000 cm ^-1. Una molécula absorberá o emitirá radiación solo si tiene un momento dipolar distinto de cero. Por lo tanto, HCl es activo por infrarrojos mientras que H ₂ y Cl ₂ no lo son.

Vibración de moléculas poliatómicas

Una molécula con átomos de N tiene un total de 3N grados de libertad para sus movimientos nucleares, ya que cada núcleo puede desplazarse independientemente en tres direcciones perpendiculares. Tres de estos grados de libertad corresponden al movimiento traslacional del centro de masa. Para una molécula no lineal, tres grados más de libertad determinan la orientación de la molécula en el espacio, y así su movimiento rotacional. Esto deja 3N - 6 modos vibracionales. Para una molécula lineal, solo hay dos grados de libertad rotacional, lo que deja 3N - 5 modos vibracionales. Por ejemplo, la molécula no lineal H ₂ O tiene tres modos vibracionales mientras que la molécula lineal CO ₂ tiene cuatro modos vibracionales. Las vibraciones consisten en movimientos coordinados de varios átomos de tal manera que se mantenga el centro de masa estacionario y no giratorio. A estos se les llama los modos normales. Cada modo normal tiene una frecuencia de resonancia característica\(\tilde{\nu _{i}}\), que generalmente se determina experimentalmente. A una aproximación razonable, cada modo normal se comporta como un oscilador armónico independiente de frecuencia\(\tilde{\nu _{i}}\). Los modos normales de H ₂ O y CO ₂ se muestran a continuación.

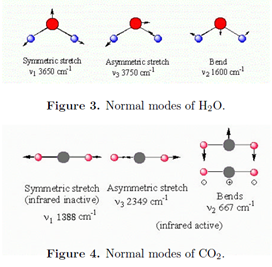
Un modo normal será infrarrojo activo sólo si implica un cambio en el momento dipolar. Los tres modos de H ₂ O están activos. El estiramiento simétrico del CO ₂ es inactivo porque los dos enlaces C-O, cada uno de los cuales es polar, compensan exactamente. Tenga en cuenta que el modo de flexión del CO ₂ es doblemente degenerado. La flexión de enlaces adyacentes en una molécula generalmente implica menos energía que el estiramiento de enlaces, por lo tanto, los modos de flexión generalmente tienen números de onda más bajos que los modos de estiramiento.

Rotación de Moléculas Diatómicas

El modelo de rotor rígido asume que la distancia internuclear R es una constante. Esta no es una mala aproximación ya que la amplitud de la vibración es generalmente del orden del 1% de R. La ecuación de Schrödinger para el movimiento nuclear involucra entonces al operador de momento angular tridimensional, escrito\(\hat{J}\) en lugar de\(\hat{L}\) cuando se refiere a la rotación molecular. Ya se conocen las soluciones a esta ecuación y podemos escribir

\[\frac{\hat{J}^2}{2\mu R^2}Y_{JM}(\theta ,\phi )=E_{J}Y_{JM}(\theta,\phi)\; \; \; J=0,1,2...\; \; \; M=0,\pm \, 1...\pm\,J\label{25}\]

donde Y _JM (\(\theta,\phi\)) son armónicos esféricos en términos de los números cuánticos J y M, en lugar de l y m. Dado que los valores propios de\(\hat{J}^2\) son\(J(J +1)\hbar^2\), los niveles de energía rotacional son

\[E_{J}=\frac{\hbar^2}{2I}J(J+1)\label{26}\]

El momento de inercia viene dado por

\[I=\mu R^2=M_{A}R^{2}_{A}+M_{B}R^{2}_{B}\label{27}\]

donde R _A y R _B son las distancias desde los núcleos A y B, respectivamente, hasta el centro de masa. En unidades de número de onda, se expresa la energía rotacional

\[hcE_{J}=BJ(J+1)cm^{-1}\label{28}\]

donde B es la constante de rotación. El diagrama de nivel de energía rotacional se muestra en la Fig.5. Cada nivel es (2J + 1) -veces degenerado. Nuevamente, solo las moléculas polares pueden absorber o emitir radiación en el transcurso de las transiciones rotacionales. La radiación se encuentra en la región de microondas o infrarrojo lejano. La regla de selección para las transiciones rotacionales es\(\Delta\) J =\(\pm\) 1.

Parámetros Moleculares de Espectroscopia

A continuación se presenta una tabla de constantes espectroscópicas para los cuatro haluros de hidrógeno:

La constante de fuerza se puede encontrar a partir de la constante vibracional. Equiparando las cantidades de energía\(\hbar\omega=hc\tilde{\nu }\), encontramos

\[\omega=2\pi c\tilde{\nu }=\sqrt{\frac{k}{\mu }}\label{29}\]

Así

\[k=(2\pi c\tilde{\nu })^2\mu\label{30}\]

con

\[\mu=\frac{m_{A}m_{B}}{m_{A}+m_{B}}=\frac{M_{A}M_{B}}{M_{A}+M_{B}}u\label{31}\]

donde u = 1.66054 x 10 ^-27 kg, la unidad de masa atómica. M _A y M _B son los pesos atómicos convencionales de los átomos A y B (en la escala ¹² C = 12). Poner en factores numéricos

\[k=58.9\, \times \, 10^{-6}(\tilde{\nu }/cm^{-1})^2\frac{M_{A}M_{B}}{M_{A}+M_{B}}N/m \label{32}\]

Esto da 958.6, 512.4, 408.4 y 311.4 N/m para HF, HCl, HBr e HI, respectivamente. Estos valores no toman en cuenta la anarmonicidad.

La distancia internuclear R está determinada por la constante de rotación. Por definición,

\[hcB=\frac{\hbar^2}{2I}\label{33}\]

Así

\[B=\frac{\hbar}{4\pi cI}\label{34}\]

con

\[I=\mu R^2=\frac{m_{A}m_{B}}{m_{A}+m_{B}}R^2=\frac{M_{A}M_{B}}{M_{A}+M_{B}}uR^2\; \; kg\: m^2\label{35}\]

Resolviendo para R,

\[R=410.6 / \sqrt{\frac{M_{A}M_{B}}{M_{A}+M_{B}}(B/cm^{-1})}\: \: pm\label{36}\]

Para los haluros de hidrógeno, HF, HCl, HBr, HI, calculamos R = 92.0, 127.9, 142.0, 161.5 pm, respectivamente.

Rotación de moléculas no lineales

Una molécula no lineal tiene tres momentos de inercia alrededor de tres ejes principales, designados I _a, I _b e I _c. La energía rotacional clásica se puede escribir

\[E=\dfrac{J^2_{a}}{2I_{a}}+\frac{J^2_{b}}{2I_{b}}+\dfrac{J^2_{c}}{2I_{c}}\label{37}\]

donde J _a, J _b, J _c son los componentes del momento angular alrededor de los ejes principales. Para un rotor esférico, como CH ₄ o SF ₆, los tres momentos de inercia son iguales al mismo valor I. La energía se simplifica a J ^2/2I y el quantomecánico Hamiltoniano viene dado por

\[\hat{H}=\frac{\hat{J}^2}{2I}\label{38}\]

Los valores propios son

\[E_{J}=\frac{\hbar^2}{2I}J(J+1)\; \;\; J=0,1,2..\label{39}\]

al igual que para una molécula lineal. Pero los niveles de un rotor esférico tienen degeneraciesof (2 J + 1) ² en lugar de (2 J + 1).

Un rotor simétrico tiene dos momentos iguales de inercia, digamos I _c = I _{b\(\neq \)} I _a. Las moléculas NH ₃, CH ₃ Cl y C ₆ H ₆ son ejemplos. El hamiltoniano toma la forma

\[ \hat H = \frac{\hat J_a^2}{2I_a}+\frac{\hat J_b^2 + \hat J_c^2}{2I_b} = \frac{\hat J^2}{2I_b} + (\frac{1}{2I_a} - \frac{1}{2I_b}) \hat J_a^2 \label{40} \]

Dado que es posible tener estados propios simultáneos de\(\hat J^2\) y uno de sus componentes\(\hat J_a\), las energías de un rotor simétrico tienen la forma

\[E_{JK}=\frac{J(J+1)}{2I_{b}}+(\frac{1}{2I_{a}}-\frac{1}{2I_{b}})K^2\; \; J=0,1,2...\; \;\; K=0\pm 1,\pm2,...\pm J\label{41}\]

Existe, además, la degeneración (2 J + 1) -fold M.

Excitaciones Electrónicas en Moléculas Diatómicas

Los estados cuánticos de las moléculas son compuestos de contribuciones rotacionales, vibracionales y electrónicas. El espaciado de energía característico de estos diferentes grados de libertad varía en muchos órdenes de magnitud, dando lugar a técnicas espectroscópicas muy diferentes para estudiar transiciones rotacionales, vibracionales y electrónicas. Las excitaciones electrónicas son típicamente del orden de varios electrón voltios, siendo 1 eV equivalente a aproximadamente 8000 cm ^-1 o 100 kJ mol ^-1. Como hemos visto, las diferencias de energía típicas son del orden de 1000 cm ^-1 para vibración y 10 cm ^-1 para rotación. La Fig. 6 da una idea general de las magnitudes relativas de estas contribuciones de energía. Cada estado electrónico tiene una estructura vibracional, caracterizada por números cuánticos vibracionales v y cada estado vibracional tiene una estructura rotacional, caracterizada por los números cuánticos rotacionales J y M.

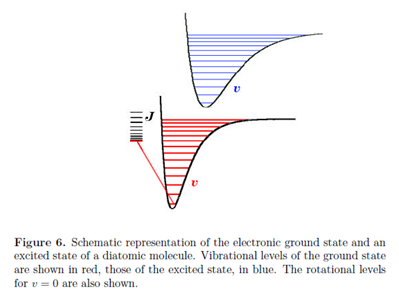
Cada transición electrónica en una molécula va acompañada de cambios en los estados vibracionales y rotacionales. Generalmente, en estado líquido, las transiciones vibracionales individuales no se resuelven, de manera que los espectros electrónicos consisten en bandas anchas que comprenden un gran número de transiciones vibracionales y rotacionales superpuestas. La espectroscopia en fase gaseosa, sin embargo, a menudo puede resolver transiciones vibracionales e incluso rotacionales individuales.

Cuando una molécula experimenta una transición a un estado electrónico diferente, los electrones se reorganizan mucho más rápidamente que los núcleos. A una muy buena aproximación, se puede considerar que el estado electrónico ocurre instantáneamente, mientras que la configuración nuclear permanece fija. Esto se conoce como el principio Franck-Condon. Tiene el mismo origen físico que la aproximación Born-Oppenheimer, es decir, la gran disparidad en las masas de electrones y nucleares. En un diagrama que muestra las energías del suelo y los estados excitados como funciones de la distancia internuclear, el comportamiento de Franck-Condon se caracteriza por transiciones verticales, en las que R permanece aproximadamente constante a medida que la molécula salta de una curva de potencial a otra.

En un estado vibracional\(\upsilon \) = 0 el máximo de probabilidad para la distancia internuclear R está cerca del centro del pozo potencial. Para todos los valores más altos, los estados vibracionales, los máximos de probabilidad ocurren cerca de los dos puntos de inflexión del potencial, donde la energía total es igual a la energía potencial. Estos corresponden en los diagramas a los puntos finales de los guiones horizontales dentro de la curva de potencial.

Colaboradores y Atribuciones

Seymour Blinder (Professor Emeritus of Chemistry and Physics at the University of Michigan, Ann Arbor)