28.4: Diferentes leyes de tasas predicen diferentes cinéticas
- Page ID
- 80488
Las leyes de tasa de diferencia predicen diferentes cinéticas
Cinética de orden cero
Si la reacción sigue una ley de tasa de orden cero, se puede expresar en términos de la tasa de tiempo de cambio de [A] (que será negativa ya que A es un reactivo):
\[-\dfrac{d[A]}{dt} = k\]
En este caso, es sencillo separar las variables. Colocación de variables de tiempo a la derecha y [A] a la izquierda
\[ d[A] = - k \,dt\]
De esta forma, es fácil de integrar. Si la concentración de A es [A] 0 en el tiempo t = 0, y la concentración de A es [A] en algún momento arbitrario después, la forma de la integral es
\[ \int _{[A]_o}^{[A]} d[A] = - k \int _{t_o}^{t}\,dt\]
que rinde
\[ [A] - [A]_o = -kt\]
o
\[ [A] = [A]_o -kt\]
Esto sugiere que una gráfica de concentración en función del tiempo producirá una línea recta, cuya pendiente es —k, y cuya intercepción es [A] 0. Si tal gráfica es lineal, entonces los datos son consistentes con la cinética de orden 0. Si no lo son, se deben considerar otras posibilidades.
Cinética de segundo orden
Si la reacción sigue una ley de tasa de segundo orden, se puede emplear alguna metodología. La tarifa se puede escribir como
\[ -\dfrac{d[A]}{dt} = k [A]^2 \label{eq1A}\]
La separación de los términos de concentración y tiempo (esta vez manteniendo el signo negativo a la izquierda por conveniencia) rinde
\[ -\dfrac{d[A]}{[A]^2} = k \,dt \]
La integración se convierte entonces
\[ - \int_{[A]_o}^{[A]} \dfrac{d[A]}{[A]^2} = \int_{t=0}^{t}k \,dt \label{eq1}\]
Y señalando que
\[ - \dfrac{dx}{x^2} = d \left(\dfrac{1}{x} \right)\]
el resultado de la integración Ecuación\ ref {eq1} es
\[ \dfrac{1}{[A]} -\dfrac{1}{[A]_o} = kt\]
o
\[ \dfrac{1}{[A]} = \dfrac{1}{[A]_o} + kt\]
Y así una trama de\(1/[A]\) como función del tiempo debería producir una gráfica lineal, cuya pendiente es\(k\), y cuya intercepción es\(1/[A]_0\).
Otras leyes de velocidad de segundo orden son un poco más difíciles de integrar, ya que la integración depende de la estequiometría real de la reacción que se está investigando. Por ejemplo, para una reacción del tipo
\[A + B \rightarrow P\]
Que tiene leyes de tarifas dadas por
\[ -\dfrac{d[A]}{dt} = k [A][B] \]
y
\[ -\dfrac{d[B]}{dt} = k [A][B] \]
la integración dependerá de la disminución de [A] y [B] (que se relacionará por la estequiometría) que se puede expresar en términos de la concentración del producto [P].
\[[A] = [A]_o – [P] \label{eqr1}\]
y
\[[B] = [B]_o – [P]\label{eqr2}\]
La concentración depende\(A\) y luego\(B\) puede ser eliminada si la ley de tarifas se expresa en términos de la producción del producto.
\[ \dfrac{d[P]}{dt} = k [A][B] \label{rate2} \]
Sustituyendo las relaciones para\([A]\) y\([B]\) (Ecuaciones\ ref {eqr1} y\ ref {eqr2}) en la expresión de ley de tasa (Ecuación\ ref {rate2}) rinde
\[ \dfrac{d[P]}{dt} = k ( [A]_o – [P]) ([B] = [B]_o – [P]) \label{rate3} \]
La separación de las variables de concentración y tiempo da como resultado
\[\dfrac{d[P]}{( [A]_o – [P]) ([B] = [B]_o – [P])} = k\,dt\]
Señalando que en su momento\(t = 0\)\([P] = 0\),, la forma integrada de la ley tarifaria se puede generar resolviendo la integral
\[\int_{[A]_o}^{[A]} \dfrac{d[P]}{( [A]_o – [P]) ([B]_o – [P])} = \int_{t=0}^{t} k\,dt\]
Consultar una tabla de integrales revela que para\(a \neq b\) [1],
\[ \int \dfrac{dx}{(a-x)(b-x)} = \dfrac{1}{b-a} \ln \left(\dfrac{b-x}{a-x} \right)\]
La aplicación de la integral definida (siempre y cuando\([A]_0 \neq [B]_0\)) da como resultado
\[ \left. \dfrac{1}{[B]_0-[A]_0} \ln \left( \dfrac{[B]_0-[P]}{[A]_0-[P]} \right) \right |_0^{[A]} = \left. k\, t \right|_0^t\]
\[ \dfrac{1}{[B]_0-[A]_0} \ln \left( \dfrac{[B]_0-[P]}{[A]_0-[P]} \right) -\dfrac{1}{[B]_0-[A]_0} \ln \left( \dfrac{[B]_0}{[A]_0} \right) =k\, t \label{finalint}\]
Sustituir ecuaciones\ ref {eqr1} y\ ref {eqr2} en Ecuación\ ref {finalint} y simplificar (combinar los términos logaritmos naturales) rinde
\[\dfrac{1}{[B]_0-[A]_0} \ln \left( \dfrac{[B][A]_o}{[A][B]_o} \right) = kt\]
Para esta ley de tasas, una parcela de\(\ln([B]/[A])\) como función del tiempo producirá una línea recta, cuya pendiente es
\[ m = ([B]_0 – [A]_0)k.\]
En el límite en\([A]_0 = [B]_0\), luego\([A] = [B]\) en todo momento, debido a la estequiometría de la reacción. Como tal, la ley de tarifas se convierte
\[ \text{rate} = k [A]^2\]
e integrar directo como en la Ecuación\ ref {EQ1a} y la ley de tasa integrada es (como antes)
\[ \dfrac{1}{[A]} = \dfrac{1}{[A]_o} + kt\]
Ejemplo\(\PageIndex{2}\): Confirming Second Order Kinetics
Considera los siguientes datos cinéticos. Utilice una gráfica para demostrar que los datos son consistentes con la cinética de segundo orden. Además, si los datos son de segundo orden, determinar el valor de la constante de velocidad para la reacción.
| tiempo (s) | 0 | 10 | 30 | 60 | 100 | 150 | 200 |
|---|---|---|---|---|---|---|---|
| [A] (M) | 0.238 | 0.161 | 0.098 | 0.062 | 0.041 | 0.029 | 0.023 |
Solución:
La trama se ve de la siguiente manera:
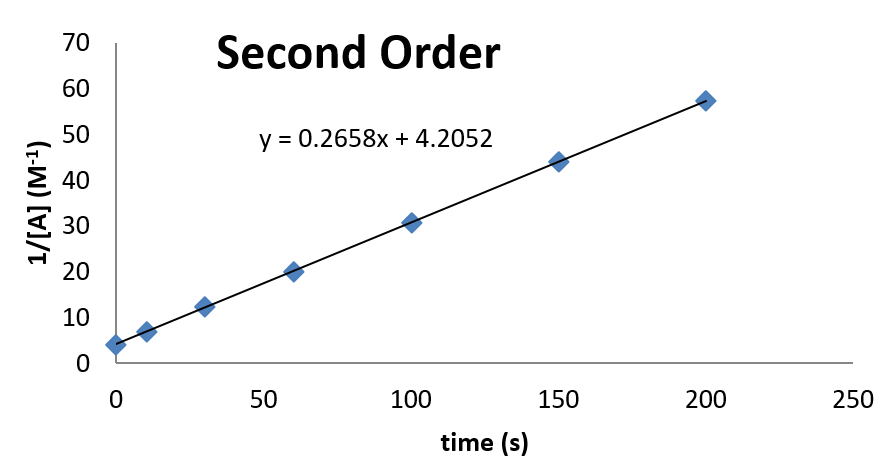
De esta parcela, se puede observar que la constante de velocidad es de 0.2658 M -1 s -1. La concentración en el momento también se\(t = 0\) puede inferir de la intercepción.
[1] Esta forma integral se puede generar utilizando el método de fracciones parciales. Véase (House, 2007) para una derivación completa.
El pentóxido de dinitrógeno (N 2 O 5) se descompone a NO 2 y O 2 a temperaturas relativamente bajas en la siguiente reacción:
\( 2N_{2}O_{5}\left ( soln \right ) \rightarrow 4NO_{2}\left ( soln \right )+O_{2}\left ( g \right ) \)
Esta reacción se lleva a cabo en una solución de CCl 4 a 45°C Las concentraciones de N 2 O 5 en función del tiempo se listan en la siguiente tabla, junto con los logaritmos naturales y las concentraciones recíprocas de N 2 O 5. Trazar una gráfica de la concentración versus t, ln concentración versus t, y 1/concentración versus t y luego determinar la ley de tasa y calcular la constante de velocidad.
| Tiempo (s) | [N 2 O 5] (M) | ln [N 2 O 5] | 1/ [N 2 O 5] (M −1) |
|---|---|---|---|
| 0 | 0.0365 | −3.310 | 27.4 |
| 600 | 0.0274 | −3.597 | 36.5 |
| 1200 | 0.0206 | −3.882 | 48.5 |
| 1800 | 0.0157 | −4.154 | 63.7 |
| 2400 | 0.0117 | −4.448 | 85.5 |
| 3000 | 0.00860 | −4.756 | 116 |
| 3600 | 0.00640 | −5.051 | 156 |
Dado: ecuación química equilibrada, tiempos de reacción y concentraciones
Preguntado por: gráfico de datos, ley de tarifas y constante de tasa
Estrategia:
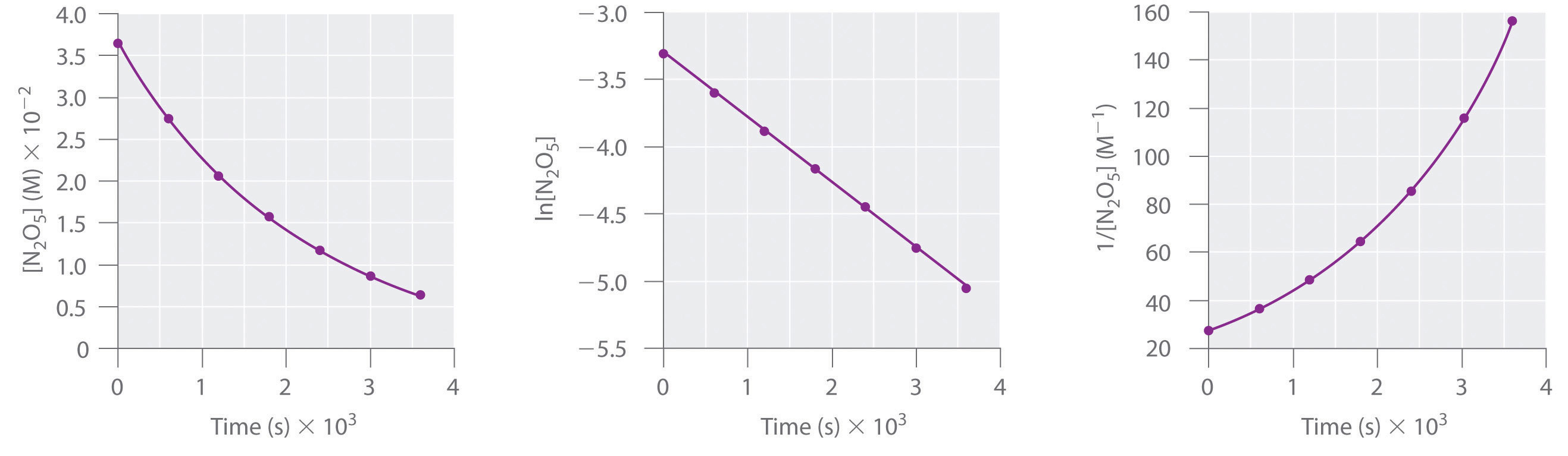
A Utilice los datos de la tabla para trazar por separado la concentración, el logaritmo natural de la concentración y el recíproco de la concentración (el eje vertical) versus el tiempo (el eje horizontal). Compare las gráficas con las de la Figura 13.4.2 para determinar el orden de reacción.
B Escribe la ley de velocidad para la reacción. Utilizando los datos apropiados de la tabla y la gráfica lineal correspondiente a la ley de velocidad para la reacción, se calcula la pendiente de la línea trazada para obtener la constante de velocidad para la reacción.
Solución:
A Aquí están las gráficas de [N 2 O 5] versus t, ln [N 2 O 5] versus t, y 1/ [N 2 O 5] versus t:
La gráfica de ln [N 2 O 5] versus t da una línea recta, mientras que las parcelas de [N 2 O 5] versus t y 1/ [N 2 O 5] versus t no lo hacen. Esto significa que la descomposición de N 2 O 5 es de primer orden en [N 2 O 5].
B Por lo tanto, la ley de velocidad para la reacción es
\( rate = k \left [N_{2}O_{5} \right ]\)
El cálculo de la constante de velocidad es sencillo porque sabemos que la pendiente de la parcela de ln [A] versus t para una reacción de primer orden es − k. Podemos calcular la pendiente utilizando dos puntos cualesquiera que se encuentren en la línea en la parcela de ln [N 2 O 5] versus t. Usando los puntos para t = 0 y 3000 s,
\( slope= \dfrac{ln\left [N_{2}O_{5} \right ]_{3000}-ln\left [N_{2}O_{5} \right ]_{0}}{3000\;s-0\;s} = \dfrac{\left [-4.756 \right ]-\left [-3.310 \right ]}{3000\;s} =4.820\times 10^{-4}\;s^{-1} \)
Así k = 4.820 × 10 −4 s −1.
Colaboradores
- Anonymous
Modified by Joshua Halpern (Howard University), Scott Sinex, and Scott Johnson (PGCC)