28.8: La teoría del estado de transición se puede utilizar para estimar las constantes de velocidad de reacción
- Page ID
- 80457
Teoría del Estado de Transición
En la Figura 28.8.1 , el punto en el que evaluamos o medimos\(E_a\) sirve como una línea divisoria (también llamada superficie divisoria) entre reactivos y productos. En este punto, no tenemos\(\text{A} + \text{B}\), y no tenemos\(\text{C}\). Más bien, lo que tenemos es un complejo activado de algún tipo llamado estado de transición entre reactivos y productos. Se denota el valor de la coordenada de reacción en el estado de transición\(q^\ddagger\). Recordemos nuestra notación\(\text{x}\) para el conjunto completo de coordenadas y momentos de todos los átomos en el sistema. Generalmente, la coordenada de reacción\(q\) es una función\(q \left( \text{x} \right)\) de todas las coordenadas y momentos, aunque típicamente,\(q \left( \text{x} \right)\) es una función de un subconjunto de las coordenadas y, posiblemente, del momento.
A modo de ejemplo, consideremos dos átomos\(\text{A}\) y\(\text{B}\) sufrir una colisión. Una coordenada de reacción apropiada podría ser simplemente la distancia\(r\) entre\(\text{A}\) y\(\text{B}\). Esta distancia es una función de las posiciones\(\textbf{r}_\text{A}\) y\(\textbf{r}_\text{B}\) de los dos átomos, en que
\[q = r = \left| \textbf{r}_\text{A} - \textbf{r}_\text{B} \right| \label{20.24} \]
Cuando\(\text{A}\) y\(\text{B}\) son moléculas, como las proteínas,\(q \left( \text{x} \right)\) es una función mucho más complicada de\(\text{x}\).
Ahora, recordemos que la energía mecánica\(\mathcal{E} \left( \text{x} \right)\) viene dada por
\[\mathcal{E} \left( \text{x} \right) = \sum_{i=1}^N \frac{\textbf{p}_i^2}{2m_1} + U \left( \textbf{r}_1, \ldots, \textbf{r}_N \right) \label{20.25} \]
y es una suma de energías cinéticas y potenciales. La teoría del estado de transición asume lo siguiente:
- El sistema es clásico, y la dependencia temporal de las coordenadas y momentos está determinada por las leyes del movimiento de Newton\[m_i \ddot{\textbf{r}}_i = \textbf{F}_i \label{20.26} \]
- Iniciamos una trayectoria obedeciendo esta ecuación de movimiento con una condición inicial\(\text{x}\) que hace\(q \left( \text{x} \right) = q^\ddagger\) y tal que\(\dot{q} \left( \text{x} \right) > 0\) para que la coordenada de reacción proceda inicial a la derecha, es decir, hacia los productos.
- Seguimos el movimiento\(\text{x}_t\) de las coordenadas y momenta en el tiempo a partir de esta condición inicial\(\text{x}\), lo que nos da una función única\(\text{x}_t \left( \text{x} \right)\).
- Si\(q \left( \text{x}_t \left( \text{x} \right) \right) > q^\ddagger\) en el momento\(t\), entonces la trayectoria se designa como “reactiva” y contribuye a la velocidad de reacción.
Definir una función\(\theta \left( y \right)\), que es\(1\) si\(y \geq 0\) y\(0\) si\(y < 0\). La función\(\theta \left( y \right)\) se conoce como una función de paso.
Ahora definimos un flujo de trayectorias reactivas\(k \left( t \right)\) usando mecánica estadística
\[k \left( t \right) = \frac{1}{h Q_r} \int_{q \left( \text{x} \right) = q^\ddagger} d \text{x} \: e^{-\beta \mathcal{E} \left( \text{x} \right)} \left| \dot{q} \left( \text{x} \right) \right| \theta \left( q \left( \text{x}_t \left( \text{x} \right) \right) - q^\ddagger \right) \label{20.27} \]
donde\(h\) está la constante de Planck. Aquí\(Q_r\) está la función de partición de los reactivos
\[Q_r = \int d \text{x} \: e^{-\beta \mathcal{E} \left( \text{x} \right)} \theta \left( q^\ddagger - q \left( \text{x} \right) \right) \label{20.28} \]
El significado de Ecuación\(\ref{20.27}\) es un promedio conjunto sobre un conjunto canónico del producto\(\left| \dot{q} \left( \text{x} \right) \right|\) y\(\theta \left( q \left( \text{x}_t \left( \text{x} \right) \right) - q^\ddagger \right)\). El primer factor en este producto\(\left| \dot{q} \left( \text{x} \right) \right|\) obliga a que la velocidad inicial de la coordenada de reacción sea positiva, es decir, hacia los productos, y la función de paso\(\theta \left( q \left( \text{x}_t \left( \text{x} \right) \right) - q^\ddagger \right)\) requiere que la trayectoria de\(q \left( \text{x}_t \left( \text{x} \right) \right)\) sea reactiva, de lo contrario, la función de paso no dará ninguna contribución al flujo. La función\(k \left( t \right)\) en la Ecuación\(\ref{20.27}\) se conoce como el flujo reactivo. En la definición de\(Q_r\) la función paso\(\theta \left( q^\ddagger - q \left( \text{x} \right) \right)\) mide el número total de estados microscópicos en el lado reactivo del perfil energético.
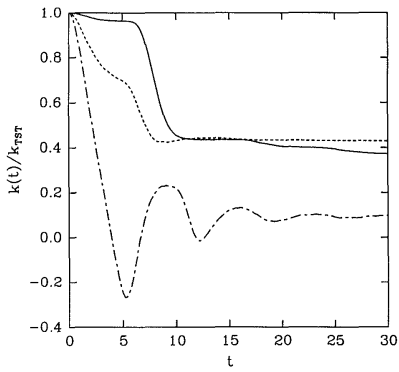
Una gráfica de algunos ejemplos de funciones de flujo reactivo\(k \left( t \right)\) se muestra en la Figura 28.8.2 . Estas funciones se discuten con mayor detalle en J. Chem. Phys. 95, 5809 (1991). Todos estos ejemplos muestran que\(k \left( t \right)\) decae al principio pero luego finalmente alcanza un valor de meseta. Este valor de meseta se toma como la velocidad real de la reacción bajo el supuesto de que eventualmente, todas las trayectorias que se volverán reactivas lo habrán hecho después de un tiempo suficientemente largo. Por lo tanto,
\[k = \underset{t \rightarrow \infty}{\text{lim}} k \left( t \right) \label{20.29} \]
da la constante de velocidad verdadera. Por otro lado, una aproximación común es tomar el valor\(k \left( 0 \right)\) como estimación de la constante de velocidad, y esto se conoce como la aproximación de la teoría del estado de transición a\(k\), es decir,
\[\begin{align} k^\text{(TST)} &= k \left( 0 \right) \\ &= \frac{1}{Q_r} \int_{q \left( \text{x} \right) = q^\ddagger} d \text{x} \: e^{-\beta \mathcal{E} \left( \text{x} \right)} \left| \dot{q} \left( \text{x} \right) \right| \theta \left( q \left( \text{x} \right) - q^\ddagger \right) \end{align} \label{20.30} \]
Sin embargo, tenga en cuenta que dado\(\dot{q} \left( \text{x} \right)\) que requerimos estar inicialmente hacia los productos, entonces por definición\(t = 0\), at\(q \left( \text{x} \right) \geq q^\ddagger\), y la función step en la expresión anterior es redundante. Además, si\(\dot{q} \left( \text{x} \right)\) solo depende de momenta (o velocidades) y no realmente de coordenadas, lo que será cierto si no\(q \left( \text{x} \right)\) es curvilíneo (y es cierto para algunas coordenadas curvilíneas\(q \left( \text{x} \right)\)), y si\(q \left( \text{x} \right)\) solo depende de coordenadas, entonces Ecuación\(\ref{20.30}\) reduce a
\[k^\text{(TST)} = \frac{1}{h Q_r} \int d \text{x}_\textbf{p} e^{-\beta \sum_{i=1}^N \textbf{p}_i^2/2m_i} \left| \dot{q} \left( \textbf{p}_1, \ldots, \textbf{p}_N \right) \right| \int_{q \left( \textbf{r}_1, \ldots, \textbf{r}_N \right) = q^\ddagger} d \text{x}_\textbf{r} e^{-\beta U \left( \textbf{r}_1, \ldots, \textbf{r}_N \right)} \label{20.31} \]
El integral
\[Z^\ddagger = \int_{q \left( \textbf{r}_1, \ldots, \textbf{r}_N \right) = q^\ddagger} d \text{x}_\textbf{r} e^{-\beta U \left( \textbf{r}_1, \ldots, \textbf{r}_N \right)} \nonumber \]
cuenta el número de estados microscópicos consistentes con la condición\(q \left( \textbf{r}_1, \ldots, \textbf{r}_N \right) = q^\ddagger\) y es, por lo tanto, una especie de función de partición, y se denota\(Q^\ddagger\). Por otro lado, debido a que es una función de partición, podemos derivar una energía libre\(\Delta F^\ddagger\) de ella
\[F^\ddagger \propto -k_B T \: \text{ln} \: Z^\ddagger \label{20.32} \]
De igual manera, si\(Q_r\) dividimos en sus contribuciones ideal-gas y configuracionales
\[Q_r = Q_r^\text{(ideal)} Z_r \label{20.33} \]
entonces podemos tomar
\[Z_r = e^{-\beta F_r} \label{20.34} \]
donde\(F_r\) está la energía libre de los reactivos. Finalmente, establecer\(\dot{q} = p/\mu\), donde\(\mu\) está la masa asociada, y\(p\) es el impulso correspondiente de la coordenada de reacción, luego, cancelando la mayoría de las integrales de impulso entre el numerador y\(Q_r^\text{(ideal)}\), la integral de impulso que necesitamos es
\[\int_0^\infty e^{-\beta p^2/2 \mu} \frac{p}{\mu} = k_B T \label{20.35} \]
que da la expresión final para la constante de velocidad de la teoría del estado de transición
\[k^\text{(TST)} = \frac{k_B T}{h} e^{-\beta \left( F^\ddagger - F_r \right)} = \frac{k_B T}{h} e^{-\beta \Delta F^\ddagger} \label{20.36} \]
Figura 28.8.2 muestra realmente\(k \left( t \right)/ k^\text{(TST)}\), que debe comenzar en\(1\). Como muestra la figura, además, para\(t > 0\),\(k \left( t \right) < k^\text{(TST)}\). Por lo tanto,\(k^\text{(TST)}\) es siempre un límite superior a la constante de tasa verdadera. La teoría del estado de transición asume que cualquier trayectoria que inicialmente se mueva hacia los productos será una trayectoria reactiva. Por esta razón, sobreestima la velocidad de reacción. En realidad, las trayectorias pueden cruzar la superficie divisoria varias o muchas veces antes de proceder eventualmente hacia los productos o hacia los reactivos.
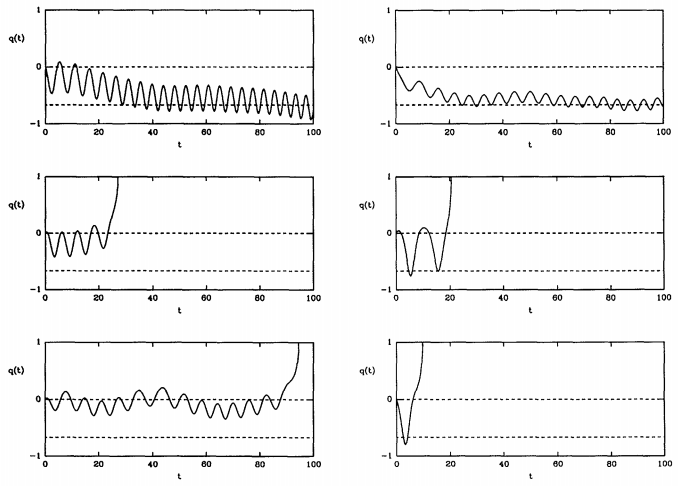
La figura 28.8.3 muestra que se pueden obtener trayectorias de ambos tipos. Aquí, la superficie divisoria se encuentra en\(q = 0\). Izquierda, hacia\(q = -1\) es el lado reactivo, y derecho, hacia\(q = 1\) es el lado del producto. Debido a que algunas trayectorias regresan a los reactivos y nunca se convierten en productos, la tasa real siempre es menor que\(k^\text{(TST)}\), y podemos escribir
\[k = \kappa k^\text{(TST)} \label{20.37} \]
donde los factores\(\kappa < 1\) is known as the transmission factor. This factor accounts for multiple recrosamientos de la superficie divisoria y el hecho de que algunas trayectorias no se convierten en reactivas.

