1.1: Supuestos básicos de la termodinámica estadística
- Page ID
- 71863
Termodinámica Basada en Mecánica Estadística
La termodinámica fenomenológica describe las relaciones entre cantidades observables que caracterizan a los objetos materiales macroscópicos. Sabemos que estos objetos consisten en un gran número de pequeñas partículas, moléculas o átomos, y, por lo que sabemos, estas pequeñas partículas se adhieren a las leyes de la mecánica cuántica y a menudo en buena aproximación a las leyes de la mecánica newtoniana. La mecánica estadística es la teoría que explica las propiedades macroscópicas, no solo las funciones de estado termodinámico, aplicando la teoría de probabilidad a las ecuaciones mecánicas de movimiento para un gran conjunto de sistemas de partículas. En esta conferencia nos preocupa la parte de la mecánica estadística que se relaciona con la termodinámica fenomenológica.
A pesar de su nombre, la termodinámica fenomenológica (equilibrio) es esencialmente una teoría estática que proporciona una descripción observacional macroscópica de la materia. La descripción mecánica subyacente es dinámica y microscópica, pero es observacional solo para sistemas que consisten en un pequeño número de partículas. Para ver esto, consideramos un sistema de partículas puntuales clásicas\(N\) idénticas que se adhieren a las ecuaciones de movimiento de Newton.
Con masa de partículas\(m\), coordenadas cartesianas\(q_i\)\((i = 1, 2, \ldots, 3N)\) y coordenadas de velocidad\(\dot{q}_i\), un sistema de partículas puntuales clásicas\(N\) idénticas evoluciona
\[\begin{align} & m \frac{\mathrm{d}^2q_i}{\mathrm{d}t^2} = -\frac{\partial}{\partial{q_i}} V\left(q_1, \ldots, q_{3N}\right) \ , \label{eq:Newtonian_eqm}\end{align}\]
donde\(V(q_1, \ldots, q_{3N})\) está la función de energía potencial.
El estado dinámico o microestado del sistema en cualquier instante se define por las coordenadas\(6N\) cartesianas y de velocidad, que abarcan el espacio dinámico del sistema. La curva del sistema en el espacio dinámico se denomina trayectoria.
El concepto se extiende fácilmente a átomos con diferentes masas\(m_i\). Si pudiéramos, en cualquier instante, medir con precisión todas las coordenadas\(6N\) dinámicas, es decir, coordenadas espaciales y velocidades, podríamos predecir con precisión la trayectoria futura. El sistema descrito por las ecuaciones newtonianas de movimientos se comporta determinísticamente.
Para cualquier sistema que los humanos puedan ver y manejar directamente, es decir, sin complicados dispositivos técnicos, el número\(N\) de partículas es demasiado grande (al menos del orden de\(10^{18}\)) para que tales mediciones completas sean posibles. Además, para sistemas tan grandes, incluso pequeños errores de medición harían inútil la predicción de trayectoria después de un tiempo bastante corto. De hecho, los átomos son objetos cuánticos y las mediciones están sujetas al principio de incertidumbre de Heisenberg, e incluso la pequeña incertidumbre introducida por eso haría inútil una descripción determinista.
Sólo podemos esperar una teoría que describa lo que podemos observar. El número de estados observacionales o macroestados que pueden ser distinguidos por el observador es mucho menor que el número de estados dinámicos. Dos sistemas clásicos en un mismo estado dinámico están necesariamente también en el mismo estado observacional, pero lo contrario no es generalmente cierto. Además, el estado observacional también evoluciona con el tiempo, pero no tenemos ecuaciones de movimiento para este estado (pero ver Sección [Liouville]). De hecho no podemos tener ecuaciones deterministas de movimiento para el estado observacional de un sistema individual, precisamente porque el mismo estado observacional puede corresponder a diferentes estados dinámicos que seguirán diferentes trayectorias.
Aún así podemos hacer predicciones, solo estas predicciones son necesariamente de naturaleza estadística. Si consideramos un gran conjunto de sistemas idénticos en el mismo estado observacional podemos incluso hacer predicciones bastante precisas sobre el resultado. Penrose da el ejemplo de una mujer en un momento en el que el diagnóstico ecográfico puede detectar el embarazo, pero no el sexo del feto. El estado observacional es el embarazo, los dos posibles estados dinámicos están en camino hacia un niño o niña. No tenemos idea de lo que sucederá en el caso individual, pero si se realiza el mismo diagnóstico a un millón de mujeres, sabemos que alrededor del 51-52% dará a luz a un niño.
¿Cómo entonces podemos derivar predicciones estables para un conjunto de sistemas de moléculas? Necesitamos considerar las probabilidades del resultado y estas probabilidades se convertirán en números exactos en el límite donde el número\(N\) de partículas (o moléculas) tiende al infinito. La teoría requerida para computar tales probabilidades será tratada en Capítulo.
Nuestro uso actual del término ensemble es flojo. Dedicaremos todo el Capítulo a aclarar qué tipos de conjuntos utilizamos en los cómputos y por qué.
El Postulado Markoviano
Existen diferentes formas de definir e interpretar las probabilidades. Para discusiones abstractas y derivaciones matemáticas la definición más conveniente es la de probabilidad física o frecuentista.
Dado un ensayo reproducible\(\mathcal{T}\) del cual\(A\) es uno de los posibles resultados, la probabilidad física\(P\) del resultado\(A\) se define como
\[\begin{align} & P(A|\mathcal{T}) = \lim\limits_{\mathcal{N} \rightarrow \infty}{\frac{n(A,\mathcal{N},\mathcal{T})}{\mathcal{N}}} \label{eq:phys_prob}\end{align}\]
donde\(n(A,\mathcal{N},\mathcal{T})\) es el número de veces que\(A\) se observa el desenlace en los primeros\(\mathcal{N}\) ensayos.
Un ensayo\(\mathcal{T}\) conforme a esta definición es estadísticamente regular, es decir, el límite existe y es el mismo para todas las series infinitas del mismo ensayo. Si se asume que la probabilidad física es una propiedad estable del sistema en estudio, se puede medir con algún error experimental. Este error experimental tiene dos contribuciones: (i) el error real de la medición de la cantidad\(A\) y (ii) la desviación de la frecuencia experimental de observación\(A\) desde el límite definido en la Ecuación\ ref {eq:phys_prob}. Contribución (ii) surge de que el número experimental de ensayos\(\mathcal{N}\) no es infinito.
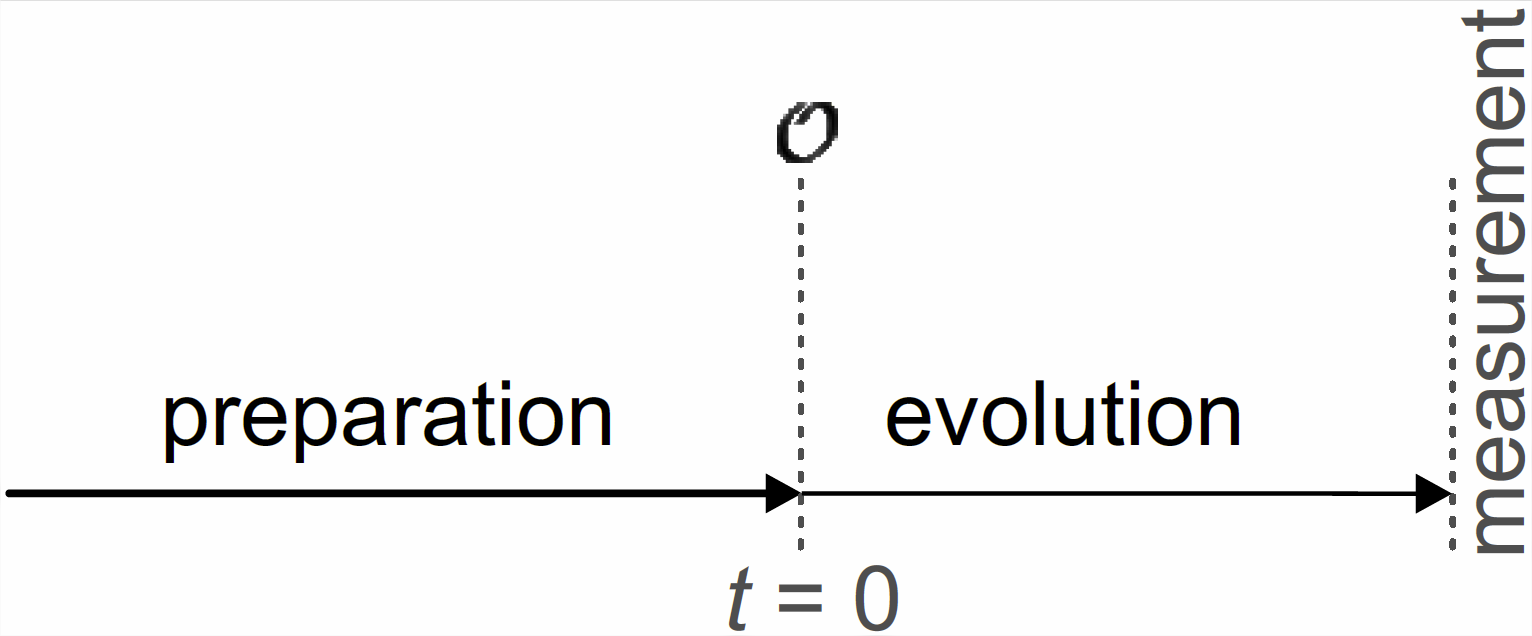
Necesitamos algún criterio que nos diga si\(\mathcal{T}\) es estadísticamente regular. Para ello dividimos el ensayo en un periodo de preparación, un periodo de evolución y la observación misma (Figura\(\PageIndex{1}\)). El periodo de evolución es un tiempo de espera durante el cual el sistema se encuentra en condiciones controladas. Junto con el periodo de preparación se necesita para cumplir con el postulado markoviano.
Un ensayo\(\mathcal{T}\) que invariablemente termina en el estado observacional\(\mathcal{O}\) del sistema después de la etapa de preparación se denomina estadísticamente regular. Al inicio del periodo de evolución se le asigna un tiempo\(t = 0\).
Obsérvese que el sistema puede estar en diferentes estados observacionales al momento de la observación; de lo contrario el postulado correspondería a un experimento trivial. El postulado markoviano se relaciona con el concepto de una cadena de eventos markovianos. En tal cadena el resultado del siguiente evento depende únicamente del estado actual del sistema, pero no de estados que se encontraron anteriormente en la cadena. Los procesos que conducen a una cadena de eventos markovianos pueden ser considerados como sin memoria.

