5.1: Conjunto canónico cuántico

Matriz de Densidad

Ocasionalmente nos hemos referido a la matriz de densidad cuántico-mecánica\(\rho\) en secciones anteriores. Antes de discutir los conjuntos cuánticos, necesitamos especificar completamente este concepto.

Los microestados que pueden ser asumidos por un sistema en un conjunto cuántico se especifican mediante un posible conjunto de funciones de onda\(\psi_i \ (i = 1\ldots r)\). La probabilidad o población del\(i^\mathrm{th}\) microestado se denota como\(P_i\), y para el caso continuo la densidad de probabilidad para una función de onda dada se denota como\(p(\psi)\). El operador de densidad es entonces dado por

\[\begin{align} & \widehat{\rho} = \sum_{i=0}^{r-1} P_i \left|\psi_i\right\rangle \left\langle \psi_i \right| \ \mathrm{(discrete)} \\ & \widehat{\rho} = \int_\psi p(\psi) \left|\psi_i\right\rangle \left\langle \psi_i \right| \ \mathrm{(continuous)} \ . \label{eq:qm_density_operator}\end{align}\]

Nótese que el caso discreto está estrechamente relacionado con el problema con los niveles de\(r\) energía que discutimos al derivar la distribución de Boltzmann para un conjunto canónico clásico. El operador de densidad se puede expresar como una matriz de densidad\(\rho\) con respecto a un conjunto de funciones base\(\left| k \right\rangle\). Para cálculos exactos, las funciones base deben formar un conjunto completo contable que permita expresar las funciones de onda del sistema\(\psi_i\) como combinaciones lineales de funciones base. Para cálculos aproximados, basta que esta combinación lineal sea una buena aproximación. Los elementos de la matriz de la matriz de densidad son dados entonces por

\[\begin{align} & \rho_{nm} = \sum_{i=0}^{r-1} P_i \left\langle m \left|\psi_i\right\rangle \left\langle \psi_i \right| n \right\rangle \ \mathrm{(discrete)} \\ & \rho_{nm} = \int_\psi p(\psi) \left\langle m\left|\psi_i\right\rangle \left\langle \psi_i \right| n \right\rangle \ \mathrm{(continuous)} \ .\end{align}\]

Con los coeficientes complejos\(c_k\) en la representación de combinación lineal\(|\psi\rangle = \sum_k c_k |k\rangle\), los elementos de la matriz son

\[\rho_{nm} = \overline{c_n c_m^\ast} \ ,\]

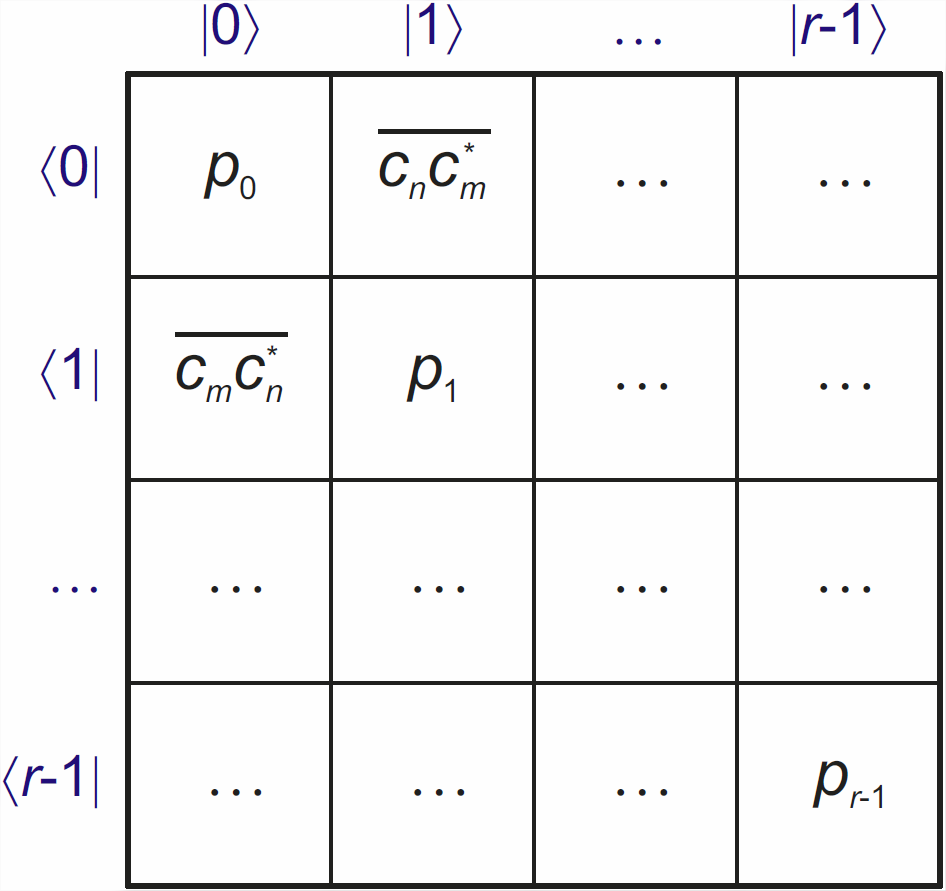
donde el asterisco denota el conjugado complejo y la barra por una vez denota el promedio del conjunto. De ello se deduce que los elementos diagonales (\(m=n\)) son necesariamente reales,\(\rho_{nn} = |c_n|^2\) y ese\(\rho_{mn}\) es el complejo conjugado de\(\rho_{nm}\). Por lo tanto, la matriz de densidad es hermitiana y el operador de densidad es autoadjoint. La dimensión matricial es el número de funciones básicas. A menudo es conveniente utilizar las funciones propias del sistema hamiltoniano\(\widehat{\mathcal{H}}\) como funciones base, pero el concepto de la matriz de densidad no se limita a esta elección. El significado de elementos de la matriz de densidad se visualiza en la Figura\(\PageIndex{1}\).

Que la matriz de densidad pueda expresarse en la base de los autoestados no implica que el conjunto pueda representarse como que consiste únicamente en autoestados, como lo afirma erróneamente Swendsen. Los elementos fuera de la diagonal de la matriz de densidad denotan superposiciones coherentes de autoestados, o coherencias cortas. Esto no es evidente en el simple ejemplo de Swendsen donde la coherencia se promedia a cero por construcción. El conjunto se puede representar como que consiste solo en estados propios si no hay coherencia. En ese caso la matriz de densidad es diagonal en la base propia. Los elementos diagonales de la matriz de densidad denotan poblaciones de estados base.

En mecánica cuántica, está bien definida qué información podemos tener sobre el macroestado de un sistema, porque las mediciones cuánticas son probabilísticas incluso para un microestado. Solo podemos observar cantidades que son observables cuántico-mecánicos y estos observables están representados por operadores\(\widehat{A}\). Se puede demostrar que el valor\(\left\langle \widehat{A} \right\rangle\) de expectativa de cualquier observable puede calcularse a partir de la matriz de densidad mediante

\[\left\langle \widehat{A} \right\rangle = \mathrm{Trace}\left\{ \widehat{\rho} \widehat{A} \right\} \ ,\]

donde hemos utilizado la notación de operador\(\widehat{\rho}\) para señalarlo\(\widehat{\rho}\) y\(\widehat{A}\) debe expresarse en la misma base.

Dado que los valores de expectativa de todos los observables son la información completa que podemos tener sobre un sistema cuántico, la matriz de densidad especifica la información completa que podemos tener sobre el conjunto. Sin embargo, la matriz de densidad no especifica completamente el conjunto en sí, es decir, no podemos inferir las probabilidades\(P_i\) o la función de densidad de probabilidad\(\rho(\psi)\) a partir de la matriz de densidad (Swendsen da un ejemplo simple). Este es otro ejemplo de la pérdida de información sobre microestados que se produce cuando solo podemos observar macroestados y que es conceptualmente equivalente a la entropía. La entropía de Von-Neumann se puede calcular a partir de la matriz de densidad mediante la ecuación\ ref {EQ:von_neumann_entropía}).

Observamos que existe una distinción importante entre las observaciones clásicas y las observaciones cuántico-mecánicas para un sistema individual. En el caso cuántico solo podemos especificar un valor de expectativa, y no se aplican los postulados segundo y tercero de Penrose (Sección [Penrose_postulados]): tampoco podemos medir simultáneamente todos los observables (pueden ser incompatibles), ni el resultado de una medición posterior es independiente de la medición actual. Sin embargo, la incertidumbre cuántica es mucho menor que los errores de medición para los grandes conjuntos que tratamos por termodinámica estadística. De ahí que los postulados de Penrose se apliquen a los conjuntos cuántico-mecánicos que representan macroestados, aunque no se aplican a los microestados.

Si todos los sistemas en un conjunto cuántico pueblan el mismo microestado, es decir, corresponden a la misma funciónondulada, se dice que el conjunto está en estado puro. Un estado puro corresponde a una entropía mínima en lugar de máxima. De lo contrario se dice que el sistema se encuentra en un estado mixto.

Función de partición cuántica

La cuantificación de energía conduce a una dificultad en el uso del conjunto microcanónico. La dificultad surge porque el conjunto microcanónico requiere energía constante, lo que restringe nuestras habilidades para asignar probabilidades en un conjunto de niveles discretos de energía. Sin embargo, como derivamos la distribución de Boltzmann, la función de partición, la entropía y todas las demás funciones de estado para los sistemas clásicos del conjunto canónico de todos modos, simplemente podemos ignorar este problema. Se considera que el conjunto canónico está en equilibrio térmico con un baño de calor (ambiente) de tamaño infinito. No importa si este baño de calor es de naturaleza mecánica clásica o cuántica. Para un sistema cuántico de tamaño infinito, el espectro de energía es continuo, lo que nos permite intercambiar energía entre el baño y cualquier sistema constituyente del conjunto canónico cuántico a voluntad.

Podemos derivar la distribución de Boltzmann y la función de partición para la matriz de densidad por analogía con el caso clásico. Para ello consideramos la matriz de densidad en la base propia. Las energías de los autoestados son los valores propios\(\epsilon_i\) de los hamiltonianos\(\mathcal{H}\). Todos los argumentos y pasos matemáticos de la Sección [subsección:Boltzmann] siguen aplicándose, con una sola excepción: La mecánica cuántica permite microestados que son superposiciones coherentes de autoestados. La derivación clásica se traslada si y sólo si podemos estar seguros de que la matriz de densidad de equilibrio puede expresarse sin contribuciones de tales microestados, lo que conduciría a elementos fuera de diagonal en la representación en la base propia de\(\mathcal{\widehat{H}}\). Este argumento efectivamente se puede hacer. Cualquier superposición de dos autoestados\(|n\rangle\) y\(|m\rangle\) con amplitudes\(|c_n|\) y\(|c_m|\) puede realizarse con diferencia de fase arbitraria\(\Delta \phi\) entre las dos funciones propias. Los microestados con el mismo\(|c_n|\) y\(|c_m|\) pero diferente\(\Delta \phi\) todos tienen la misma energía. La entropía de un subconjunto que puebla estos microestados es máxima si la distribución de las diferencias de fase\(\Delta \phi\) es uniforme en el intervalo\([0,2\pi)\). En ese caso se\(\overline{c_m^\ast c_n}\) desvanece, es decir, tales subconjuntos no aportarán elementos fuera de diagonal a la matriz de densidad de equilibrio.

Ahora podemos organizar el\(e^{-\epsilon_i/k_\mathrm{B} T}\) en forma de matriz,

\[\xi = e^{-\mathcal{\widehat{H}}/k_\mathrm{B} T} \ ,\]

con los elementos de la matriz\(\xi_{ii} = e^{-\epsilon_i/k_\mathrm{B} T}\) y\(\xi_{ij} = 0\) para\(i \neq j\). La función de partición es la suma de todos los elementos diagonales de esta matriz, es decir, la traza de\(\xi\). Por lo tanto,

\[\widehat{\rho}_\mathrm{eq} = \frac{e^{-\mathcal{\widehat{H}}/k_\mathrm{B} T}}{\mathrm{Trace}\left\{ e^{-\mathcal{\widehat{H}}/k_\mathrm{B} T} \right\}} \ , \label{eq:rho_eq} \]

donde hemos utilizado la notación de operador. Esto implica que la Ecuación\ ref {eq:rho_eq} puede evaluarse en cualquier base, no solo la base propia de\(\widehat{\mathcal{H}}\). En una base diferente, se\(e^{-\epsilon_i/k_\mathrm{B} T}\) necesita computar como una matriz exponencial y, en general, la matriz de densidad\(\rho_\mathrm{eq}\) tendrá elementos fuera de diagonal distintos de cero en una base tan diferente.

La función de partición cuántico-mecánica,

\[Z = \mathrm{Trace}\left\{ e^{-\mathcal{\widehat{H}}/k_\mathrm{B} T} \right\} \ , \label{eq:qm_z} \]

es independiente de la elección de la base, ya que la traza de una matriz es invariante bajo transformaciones unitarias. Tenga en cuenta que hemos utilizado un capital\(Z\) para una función de partición molecular. Esto es apropiado, ya que el rastro de\(\widehat{\rho}_\mathrm{eq}\) en la Ecuación\ ref {eq:rho_eq} es la unidad. En la base propia, los elementos diagonales de\(\rho_\mathrm{eq}\) son las poblaciones de los autoestados en equilibrio térmico. No hay coherencia para un conjunto cuántico suficientemente grande en equilibrio térmico.

Observamos que la matriz de densidad en equilibrio térmico puede derivarse de una manera más estricta considerando explícitamente un sistema que incluya tanto el conjunto canónico como el baño de calor y ya sea trazando los grados de libertad del baño de calor o confiando en una expansión en serie que se reduzca a solo dos términos en el límite de un baño de calor infinito.

Al acercarse a la temperatura absoluta cero, el elemento matriz de\(\rho\) en la base propia que corresponde a la energía más baja\(\epsilon_i\) se vuelve mucho mayor que todos los demás. At\(T=0\), el estado fundamental correspondiente está poblado exclusivamente y el conjunto está en estado puro si solo hay un estado con esta energía. Porque por\(T \rightarrow \infty\) otro lado, las diferencias entre los elementos de la matriz diagonal desaparecen y todos los estados están igualmente poblados. El conjunto se encuentra en un estado máximo mixto.