8.2: Termodinámica de Soluciones

Objetivos de aprendizaje

Asegúrese de comprender a fondo las siguientes ideas esenciales:

• Describir los dos procesos fundamentales que deben ocurrir cada vez que un soluto se disuelve en un solvente, y discutir los efectos de la absorción o liberación de energía en la extensión de estos procesos.
• Otro factor que entra en el proceso de formación de la solución es el aumento (u ocasionalmente, la disminución) en la entropía —es decir, el grado en que se dispersa o “diluye” la energía térmica. Explique esto en sus propios términos.
• Explique cómo el adagio “como se disuelve como” refleja los efectos mencionados anteriormente. ¿Cuál es la principal propiedad física de una molécula que define esta “semejanza”?
• ¿Qué queremos decir cuando describimos un líquido como el agua como “asociado”? Explique cómo esto se relaciona con la solubilidad de los solutos en dichos líquidos.

Se puede recordar que en la unidad anterior sobre equilibrios de fase, señalamos que las agregaciones de moléculas que están más desordenadas tienden a ser las que se favorecen a mayor temperatura, mientras que las que poseen la menor energía potencial son favorecidas a temperaturas más bajas. Este es un principio general que se aplica en todo el mundo de la materia; la forma estable a cualquier temperatura dada siempre será aquella que conduzca al mejor equilibrio entre la energía de bajo potencial y el trastorno de alto peso molecular. Para ver cómo se aplican estas consideraciones a las soluciones, piense en los pasos individuales que deben llevarse a cabo cuando un soluto se disuelve en un disolvente:

1. Si el soluto es sólido o líquido, primero debe dispersarse —es decir, sus unidades moleculares deben separarse. Esto requiere energía, por lo que este paso siempre funciona contra la formación de soluciones.

2. Después, el soluto debe introducirse en el disolvente. Si esto es energéticamente favorable o desfavorable depende de la naturaleza del soluto y disolvente. Si el soluto es A y el disolvente es B, entonces lo importante es la fuerza de las fuerzas de atracción entre las moléculas A-A y B-B, en comparación con las que se encuentran entre pares A-B; si estas últimas son mayores, entonces la energía potencial será menor cuando se mezclen las sustancias y se favorecerá la formación de solución.

Si la etapa 2 libera más energía de la que se consume en la etapa 1, esto favorecerá la formación de la solución, y generalmente podemos esperar que el soluto sea soluble en el disolvente. Aunque el proceso de disolución sea ligeramente endotérmico, existe un tercer factor importante, el aumento de la entropía, que muy a menudo favorecerá el estado disuelto.

Entropía de Solución

Como sabe cualquiera que haya barajado una baraja de cartas, los arreglos desordenados de los objetos son estadísticamente más favorecidos simplemente porque hay más formas en las que se pueden realizar. Y a medida que aumenta el número de objetos, más gobiernan las estadísticas sus arreglos más probables. El número de objetos (moléculas) con los que tratamos en Química es tan grande que su tendencia a extenderse lo más posible se vuelve abrumadora. Sin embargo, al hacerlo, la energía térmica que llevan consigo también se esparce y dispersa, por lo que la disponibilidad de esta energía, medida por la temperatura, también es de importancia. Los químicos utilizan el término “entropía” para denotar este aspecto de la aleatoriedad molecular.

Los lectores de esta sección que hayan tenido alguna exposición a la termodinámica sabrán que la solubilidad, como todos los equilibrios, se rige por el cambio de energía libre de Gibbs para el proceso, que incorpora el cambio de entropía a nivel fundamental. Una comprensión adecuada de estas consideraciones requiere cierta familiaridad con la termodinámica, que la mayoría de los estudiantes no encuentran hasta bien entrado su segundo semestre de Química. Si aún no estás ahí, no te desesperes; por la presente se te concede permiso temporal para pensar en el “desorden” molecular y la entropía simplemente en términos de “extensión de salida”.

Así, en el caso muy común en el que una pequeña cantidad de sólido o líquido se disuelve en un volumen mucho mayor de disolvente, el soluto se vuelve más extendido en el espacio, y el número de formas equivalentes en las que el soluto puede distribuirse dentro de este volumen aumenta considerablemente. Esto es lo mismo que decir que la entropía del soluto aumenta.

Si las energéticas de disolución son favorables, este incremento en la entropía significa que siempre se cumplirán las condiciones de solubilidad. Aunque la energética sea ligeramente endotérmica, el efecto de entropía aún puede permitir que se forme la solución, aunque quizás limitando la concentración máxima que se pueda lograr. En tal caso, podemos describir el soluto como ligeramente soluble en cierto disolvente. Lo que esto significa es que se requerirá un mayor volumen de disolvente para disolver completamente una masa dada de soluto.

Entalpía de la Solución

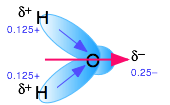
Las moléculas polares son aquellas en las que la carga eléctrica se distribuye asimétricamente. El ejemplo más familiar es el agua ordinaria, en la que el átomo de oxígeno altamente electronegativo tira parte de la nube de carga eléctrica asociada con cada enlace O-H más cerca de sí mismo. Aunque la molécula H ₂ O es eléctricamente neutra en general, este desequilibrio de carga da lugar a un momento dipolo eléctrico permanente.

Los químicos utilizan el término líquidos “asociados” para referirse a líquidos en los que los efectos de los enlaces de hidrógeno dominan la estructura local. El agua es el más importante de estos, pero el amoníaco NH ₃ y el cianuro de hidrógeno HCN son otros ejemplos comunes.

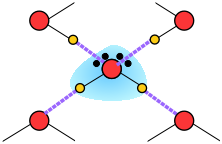
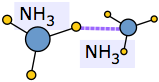
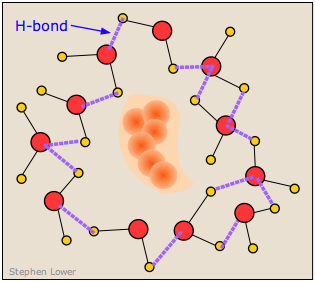
Así, el agua líquida consiste en una red extendida de moléculas H ₂ O unidas entre sí por atracciones dipolo-dipolo que llamamos enlaces de hidrógeno. Debido a que estos son mucho más débiles que los enlaces químicos ordinarios, continuamente están siendo interrumpidos por las fuerzas térmicas. Como resultado, la estructura extendida está altamente desordenada (en contraste con la del hielo sólido) y cambia continuamente.

Cuando se introduce una molécula de soluto en un líquido asociado, se debe gastar una cierta cantidad de energía para romper la estructura local de enlaces de hidrógeno y hacer espacio para la nueva molécula. Si el soluto es en sí mismo un ion o una molécula polar, entran en juego nuevas atracciones ión-dipolo o dipolo-dipolo. En casos favorables, estos pueden liberar suficiente energía potencial para compensar en gran medida la energía requerida para incorporar el soluto a la estructura.

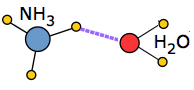
Un ejemplo extremo de esto ocurre cuando el amoníaco se disuelve en agua. Cada molécula NH ₃ puede formar tres enlaces de hidrógeno, por lo que la solución resultante está aún más unida a hidrógeno que el agua pura, lo que representa la considerable cantidad de calor liberado en el proceso y la solubilidad extraordinariamente grande del amoníaco en el agua.

Los solutos no polares son escasamente solubles en agua: el efecto hidrofóbico

Cuando un soluto no polar como el oxígeno o el hexano se introduce en un líquido asociado, podríamos esperar que la energía requerida para romper los enlaces de hidrógeno para hacer espacio para la nueva molécula no sea compensada por la formación de nuevas interacciones atractivas, lo que sugiere que el proceso será energéticamente desfavorable. Por lo tanto, podemos predecir que los solutos de este tipo solo serán escasamente solubles en agua, y este es efectivamente el caso.

Resulta, sin embargo, que esta no es una explicación del todo correcta para la pequeña solubilidad de los solutos no polares en el agua. Ahora se sabe que las moléculas H ₂ O que rodean a un intruso no polar y se encuentran incapaces de formar interacciones polares o unidas por hidrógeno que disminuyen la energía con él se reorganizarán en una configuración que maximiza el enlace de hidrógeno entre las propias moléculas de agua. Al hacerlo, esto crea un caparazón similar a una jaula alrededor de la molécula de soluto. En términos de la energética del proceso, estas nuevas interacciones H ₂ O-H ₂ O compensan en gran medida la falta de interacciones soluto-H ₂ O.

Sin embargo, esta capa de moléculas de agua altamente organizadas cobra su propio costo en la solubilidad al reducir la entropía del sistema. La disolución de un soluto normalmente aumenta la entropía al esparcir las moléculas de soluto (y la energía térmica que contienen) a través del mayor volumen del disolvente. Pero en este caso, las moléculas H ₂ O dentro de la cubierta altamente estructurada que rodea a la molécula de soluto están restringidas a esta ubicación, y su número es lo suficientemente grande como para reducir la entropía mucho más de lo que el soluto disuelto la incrementa.

Las implicaciones del efecto hidrofóbico van mucho más allá del tema de la solubilidad. Gobierna la forma en que se pliegan las proteínas, la formación de burbujas de jabón y la formación de membranas celulares. La pequeña solubilidad de un soluto no polar en un líquido asociado, como el agua, resulta más del cambio negativo de la entropía que de consideraciones energéticas. Este fenómeno se conoce como el efecto hidrofóbico. En la siguiente sección, exploraremos las formas en que estas consideraciones de energía y entropía se unen en diversos tipos de soluciones.