1.7: Errores en la medición

Las mediciones científicas no tienen ningún valor (o al menos, no son realmente científicas) a menos que se den con alguna declaración de los errores que contienen. Si una encuesta informa que un candidato lidera a otro en un 5%, eso puede ser políticamente útil para que el candidato ganador lo señale. Pero todas las encuestas respetables son científicas, y reportan errores. Si el error en la medición es más o menos 10%, lo que indica algo desde el candidato liderando un 15% hasta un arrastre en un 5%, la encuesta realmente no dice de manera confiable quién está a la cabeza. Si la encuesta tuviera un error de 1%, el candidato líder podría hacer un caso más científico que por estar en la cabeza (por un margen de 4% a 6%, o 5% +/ -1%).

Por suerte, tenemos un método fácil para indicar el error en una medición, y se sugiere en los resultados que dimos para un experimento de contaminación del aire, en el que la masa de humo recolectada se dio como 3.42 × 10 ^—2 g y el volumen del globo se dio como 1.021 926 4 × 10 ⁷ cm ³.

“Cifras significativas”

El volumen se calculó a partir de un diámetro de balón de 106 pulgadas. Sin embargo, hay algo extraño en la segunda cantidad. Contiene un número que se copió directamente de la pantalla de una calculadora electrónica y tiene Demasiados Dígitos para representar correctamente el error de medición.

La confiabilidad (más específicamente, el error aleatorio o precisión) de una cantidad derivada de una medición se indica habitualmente por el número de cifras significativas (o dígitos significativos) que contiene. Por ejemplo, los tres dígitos significativos en la cantidad 3.42 × 10 ^—2 g nos indican que se utilizó un saldo en el que podríamos distinguir 3.42 × 10 ^—2 g de 3.43 × 10 ^—2 o 3.41 × 10 ^—2 g Podría haber alguna duda sobre el último dígito, pero los que están a la izquierda de se toman como completamente confiables. Otra forma de indicar lo mismo es (3.42±0.01) × 10 ^—2 g Nuestra medición está en algún lugar entre 3.41 × 10 ^—2 y 3.43 × 10 ^—2 g.

Para ilustrar cómo el número de dígitos significativos indica el error, supongamos que tenemos una medición reportada como 3.42 g. A partir de la medición, supondríamos un error de 0.01 g, y el error porcentual es

\[ \text{Percent Error } = \dfrac{\text{Error}}{\text{Value}} \times 100\%\label{1} \]

\[ \text{Percent Error} = \dfrac{0.01 \text{ g}}{3.42 \text{ g}} \times 100\% = 0.29\% \nonumber \]

Si la medición correctamente registrada tuviera más dígitos, como 3.4275 g, la medición en sí indicaría que se utilizó una balanza más cara para dar una mejor precisión (un error porcentual menor). En este caso, el error es de 0.0001 g, y el error porcentual es:

\[ \text{Percent Error} = \dfrac{0.0001 \text{ g}}{3.4265 \text{ g}} \times 100\% = 0.0029\% \nonumber \]

Por lo que registramos las mediciones al número adecuado de dígitos como método rudimentario ^[1] para indicar su error aproximado.

 

Figura\(\PageIndex{1}\) El nivel de un líquido en un cilindro graduado. La superficie en forma de platillo de un líquido en un tubo se llama menisco.

Ilustración de una parte de un cilindro graduado lleno de un líquido. La superficie líquida tiene una curvatura hacia abajo que desprende una lectura de 38 centímetros en cubos.

Ejemplo\(\PageIndex{1}\): Graduated Cylinder

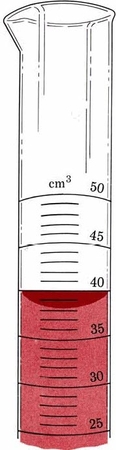
Como otro ejemplo de elegir un número apropiado de dígitos significativos, leamos el volumen de líquido en un cilindro graduado.

Solución:

El fondo del menisco se encuentra entre graduaciones correspondientes a 38 y 39 cm ³. Podemos estimar que está a 38.5 cm ³, pero el último dígito podría estar fuera un poco, quizás te parezca 38.4 o 38.6 cm ³. Dado que el tercer dígito está en cuestión, deberíamos usar tres cifras significativas. El volumen se registraría como 38.5 cm ³, lo que indica un error de 0.1 cm ³. El equipo de laboratorio a menudo se calibra de manera similar a este cilindro graduado; se debe estimar a la décima más cercana de la graduación más pequeña.

Contando Dígitos Significativos

En algunos números ordinarios, por ejemplo, 0.001 23, los ceros sirven meramente para localizar el punto decimal. No indican la confiabilidad de la medición y por lo tanto no son significativas. Otra ventaja de la notación científica es que podemos suponer que todos los dígitos son significativos. Así, si 0.001 23 se escribe como 1.23 × 10 ^—3, solo se escriben los 1, 2 y 3, que indican la confiabilidad de la medición. El punto decimal se ubica por la potencia de 10.

Si se aplica la regla expresada en el párrafo anterior al volumen de aire recolectado en nuestro experimento de contaminación, 1.021 926 4 × 10 ⁷ cm ³, encontramos que el volumen tiene ocho dígitos significativos. Esto implica que se determinó a ±1 cm ³ de alrededor de 10 millones de cm ³, una confiabilidad que corresponde a ubicar a un saltamontes exactamente en algún punto de la carretera de Filadelfia a la ciudad de Nueva York. Para experimentos tan crudos como el nuestro, esto no es probable. Veamos qué tan buena fue la medición.

Recordará que calculamos el volumen a partir del diámetro del globo, 106 pulg. Las tres cifras significativas implican que esto podría haber sido tan grande como 107 pulgadas o tan pequeño como 105 pulgadas. Podemos repetir el cálculo con cada una de estas cantidades para ver qué tan lejos estaría el volumen:

\(\begin{align} & \text{ }r\text{ = }\dfrac{\text{1}}{\text{2}}\text{ }\times \text{ 107 in = 53}\text{.5 in }\times \text{ }\dfrac{\text{1 cm}}{\text{0}\text{.3937 in}}\text{ } \\ & \text{ = 135}\text{.890 27 cm} \\ & \text{ }V\text{ = }\dfrac{\text{4}}{\text{3}}\text{ }\times \text{ 3}\text{.141 59 }\times \text{ (135}\text{.890 27 cm)}^{\text{3}}\text{ } \\ & \text{ = 10 511 225 cm}^{\text{3}}\text{ = 1}\text{.051 122 5 }\times \text{ 10}^{\text{7}}\text{ cm}^{\text{3}} \\ & \text{or }V\text{ = }\dfrac{\text{4}}{\text{3}}\text{ }\times \text{ 3}\text{.141 59 }\times \text{ }\left( \dfrac{\text{1}}{\text{2}}\text{ }\times \text{ 105 in }\times \text{ }\dfrac{\text{1 cm}}{\text{0}\text{.3937 in}} \right)^{\text{3}}\text{ } \\ & \text{ = 9 932 759 cm}^{\text{3}}\text{ = 0}\text{.993 275 9 }\times \text{ 10}^{\text{7}}\text{ cm}^{\text{3}} \\ \end{align}\)

Es decir, el volumen está entre 0.99 × 10 ⁷ y 1.05 × 10 ⁷ cm ³ o (1.02 ± 0.03) × 10 ⁷ cm ³. Deberíamos redondear nuestro resultado a tres cifras significativas, por ejemplo, 1.02 cm³, porque el último dígito, es decir, 2, está en duda.

Entonces la conclusión es simple: El resultado calculado no puede ser más preciso que la medición a partir de la cual se realizó. Para mostrar esto de manera alternativa, el error en 106 in sería de aproximadamente 1 pulgada, por lo que el porcentaje de error es

\[ \text{Percent Error} = \dfrac{1 \text{ in}}{106 \text{ in}} \times 100\% = 0.9\% \nonumber \]

Si el resultado se reporta como 10 219 264 cm ³, el error implícito es 1 parte en 10 219 264 y el porcentaje de error es:

\[ \text{Percent Error} = \dfrac{1 \text{ cm}^{\text{3}}}{10219264 \text{ cm}^\text{3}} \times 100\% = 0.000009\% \nonumber \]

Claramente, no deberíamos poder aumentar la precisión de nuestros datos simplemente manipulando los datos matemáticamente, por lo que necesitamos reglas simples para redondear números en cantidades calculadas.

Si el resultado se reporta correctamente como 1.02 × 10 ⁷ cm ³, el porcentaje de error es

\[ \text{Percent Error} = \dfrac{0.01 \text{ cm}^{\text{3}}}{1.02 \text{ cm}^\text{3}} \times 100\% = 1\% \nonumber \],

aproximadamente la misma que la medición original.

Reglas para redondear números

1. Todos los dígitos a redondear se eliminan juntos, no uno a la vez.
2. Si el dígito más a la izquierda que se va a eliminar es menor de cinco, el último dígito retenido no se altera.
3. Si el dígito más a la izquierda que se va a eliminar es mayor que cinco, el último dígito retenido se incrementa en uno.
4. Si el dígito más a la izquierda a eliminar es cinco y al menos uno de los otros dígitos a eliminar no es cero. el último dígito retenido se incrementa en uno.
5. Si el dígito que más a la izquierda le quitó es cinco y todos los demás dígitos a eliminar son cero, el último dígito retenido no se altera si es par, sino que se incrementa en uno si es impar.

La aplicación de las Reglas para Redondear Números se puede ilustrar con un ejemplo.

Ejemplo\(\PageIndex{2}\) : Rounding

Redondear cada uno de los números a continuación a tres cifras significativas.

1. 34.7449
2. 34.864
3. 34.754
4. 34.250
5. 34.35

Solución
a) Aplicar reglas 1 y 2:

 

449 son dígitos a eliminar. La flecha apunta a 7 como el último dígito retenido y eso es menos de cinco. Los resultados finales muestran 34.7.

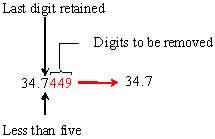
(Tenga en cuenta que se obtendría un resultado diferente si los dígitos se redondearan incorrectamente uno a la vez desde la derecha).

b) Aplicar reglas 1 y 3:34.8 64 → 34.9

c) Aplicar reglas 1 y 4:34.7 54 → 34.8

d) Aplicar reglas 1 y 5:34.2 50 → 34.2

e) Aplicar regla 5:34.3 5 → 34.4

¿A cuántas cifras significativas debemos redondear nuestros resultados de contaminación del aire? Ya hemos hecho un cálculo que implica multiplicación y división para obtener el volumen de nuestro globo colector de gas. Se trata de las siguientes cantidades y números:

un cálculo que implica multiplicación y división para obtener el volumen de nuestro globo colector de gas

\( 106 \text{ in}\)	Una cantidad medida con tres cifras significativas
\ (106\ text {in}\)” style="text-align:center; ">\( 0.3937 \text{ in/cm}\)	Un factor de conversión dado con cuatro cifras significativas ^(1)
\ (106\ text {in}\)” style="text-align:center; ">\(3.141 59\)	π usado con seis cifras significativas (podríamos obtener más si quisiéramos)
\ (106\ text {in}\)” style="text-align:center; ">\(\tfrac{\text{4}}{\text{3}} \text{ and } \tfrac{\text{1}}{\text{2}}\)	Números ^(2) con un número infinito de cifras significativas ya que los números enteros en estas fracciones son exactos por definición

1. algunos factores de conversión como 1 mg = 0.001 g son exactos, y tienen un número infinito de cifras significativas).
2. Tenga en cuenta que los números puros no son medidas ni cantidades, por lo que son ilimitados en el número de cifras significativas (los números tienen error cero).

El resultado del cálculo contenía tres cifras significativas, las mismas que el número menos confiable. Esto ilustra la regla general de que para la multiplicación y división el número de cifras significativas en el resultado es el mismo que en la medición menos confiable. Se supone que los números definidos como π, ½ o 100 cm/1m tienen un número infinito de cifras significativas.

En el caso de suma y resta, se aplica una regla diferente. Supongamos, por ejemplo, que pesamos un filtro de recolección de humo en una balanza relativamente inexacta que solo podría leerse al 0.01 g más cercano. Después de recolectar una muestra, el filtro se volvió a pesar en una balanza de una sola sartén para determinar la masa de partículas de humo.

• Masa final: 2.374 5 g (los dígitos coloreados están en cuestión)
• Masa inicial: —2.3 2 g
• Masa de humo: 0.0 545 g

Dado que el pesaje inicial podría haber sido de 2.31 a 2.33 g, las tres cifras del resultado final están en duda. (Debe estar entre 0.0445 y 0.0645 g). Por lo tanto, no hay más que un dígito significativo, y el resultado es de 0.05g. La regla aquí es que el resultado de suma o resta no puede contener más dígitos a la derecha de los que hay en ninguno de los números sumados o restados. Tenga en cuenta que la resta puede reducir drásticamente el número de dígitos significativos cuando se aplica esta regla.

Redondear números es especialmente importante si se utiliza una calculadora electrónica, ya que estas máquinas suelen mostrar una gran cantidad de dígitos, la mayoría de los cuales carecen de sentido. El mejor procedimiento es llevar todos los dígitos hasta el final del cálculo (¡a tu calculadora no le importará el trabajo extra!) y luego redondear apropiadamente. Las respuestas a los cálculos posteriores en este libro se redondearán de acuerdo con las reglas dadas. Es posible que desee volver a los ejemplos anteriores y redondear sus respuestas correctamente también.

Ejemplo\(\PageIndex{3}\): Significant Figures

Evaluar las siguientes expresiones, redondeando la respuesta al número apropiado de cifras significativas.

1. \(32.61 \text{g} + 8.446 \text{g} + 7.0 \text{g} \)
2. \(0.136 \text{cm}^3 \times 10.685 \text{g cm}^{-3}\)

Solución

1. \(32.61 \text{g} + 8.446 \text{g} + 7.0 \text{g} = 48.056 \text{g} = 48.1 \text{g (7.0 has only one figure to the right of the decimal point.)}\)
2. \(0.136 \text{cm}^3 \times 10.685 \text{g cm}^{-3} = 1.453 \text{g} = 1.45 \text{g (0.136 has only three significant figures.)}\)

Precisión vs. precisión

Cuando sugerimos llenar un globo meteorológico excedente para medir la cantidad de gas que se bombeó a través de nuestro colector de contaminación del aire, mencionamos que esta sería una forma bastante cruda de determinar el volumen. Por un lado, no sería tan sencillo medir el diámetro de una esfera de 8 o 9 pies de manera confiable. Usando una vara de medir, tendríamos la suerte de tener medidas sucesivas acordadas dentro de media pulgada más o menos. Fue por esta razón que el resultado se reportó a la pulgada más cercana. El grado en que las mediciones repetidas de la misma cantidad dan el mismo resultado se denomina precisión. La repetición de una medición altamente precisa produciría resultados casi idénticos, mientras que la baja precisión implica que los números diferirían en un porcentaje significativo entre sí.

Se podría lograr una medición muy precisa del diámetro de nuestro globo, pero probablemente no valdría la pena. Hemos asumido una forma esférica, pero es casi seguro que esto no es exactamente correcto. No importa cuán precisamente determinemos el diámetro, nuestra medición del volumen de gas estará influenciada por desviaciones de la forma asumida. Cuando uno o más de nuestros supuestos sobre un instrumento de medición son erróneos, la precisión de un resultado se verá afectada. Un ejemplo obvio sería una regla de pie dividida en 11 pulgadas iguales. Las mediciones que emplean este instrumento podrían estar de acuerdo con mucha precisión, pero no serían muy precisas. Los siguientes datos sobre la masa del humo, medidos repetidamente con dos balanzas y una escala, muestran la diferencia entre exactitud y precisión. Si se ha determinado que la masa es exactamente 0.03420 g mediante una medición independiente, la primera balanza es a la vez precisa (se obtiene el valor correcto) y precisa (el rango de mediciones es pequeño); la segunda balanza es precisa, pero no precisa; la escala no es precisa ni precisa. Tenga en cuenta que estamos comparando los tres entre sí; en relación con un saldo que tuvo un rango de 0.00001 g, los tres serían imprecisos.

Tabla\(\PageIndex{1}\): Mediciones Precisas vs Precisas

	Masa, Equilibrio A	Masa, Equilibrio B	Masa, Escala
	0.0342	0.0362	0.0380
	0.0341	0.0361	0.0370
	0.0342	0.0363	0.0390
	0.0343	0.0362	0.0400
promedio	0.0342	0.0362	0.0385
gama	0.001	0.001	0.013

Las siguientes cifras ayudan a comprender la diferencia entre precisión (pequeña diferencia esperada entre múltiples mediciones) y precisión (diferencia entre el resultado y un valor conocido).

Figura\(\PageIndex{1}\): (izquierda) Alta precisión y baja precisión. (centro izquierdo) Baja precisión y alta precisión. (centro derecho) Alta precisión y baja precisión. (centro izquierda) Baja precisión y baja precisión (dominio público; DarkEvil)

Un punto importante de otro tipo se ilustra en los dos últimos párrafos. Se han adoptado muchas palabras comunes en el lenguaje de la ciencia. Por lo general, tal adopción va acompañada de una definición científica inequívoca que no aparece en un diccionario normal. La precisión y la precisión se tratan muchas veces como sinónimos, pero en la ciencia cada uno tiene un significado ligeramente diferente. Otro ejemplo es la cantidad, que hemos definido en términos de “número × unidad”. Otras palabras en inglés como bulto, tamaño, cantidad, etc., pueden ser sinónimos de cantidad en el habla cotidiana, pero no en la ciencia. A medida que te encuentres con otras palabras como esta, trata de aprender y usar la definición científica lo antes posible, y evita confundirla con los otros significados que ya conoces.

Incluso otorgando la crudeza de las mediciones que acabamos de describir, serían adecuadas para demostrar si existía o no un problema de contaminación del aire. El siguiente paso sería encontrar un químico o funcionario de salud pública que fuera experto en evaluar la calidad del aire, presentar sus datos y convencer a esa persona de que preste su habilidad y autoridad a su argumento de que algo andaba mal. Dicha persona tendría a su disposición equipo cuya precisión y exactitud fueran adecuadas para mediciones altamente confiables y podría hacer declaraciones públicas autorizadas sobre la magnitud del problema de la contaminación del aire.