16.4: Energía Gibbs
- Page ID
- 75151
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Definir la energía libre de Gibbs y describir su relación con la espontaneidad
- Calcular el cambio de energía libre estándar para un proceso utilizando energías libres estándar de formación para sus reactivos y productos
- Calcular el cambio de energía libre estándar para un proceso usando sentalpías de formación y las entropías para sus reactivos y productos
- Explicar cómo la temperatura afecta la espontaneidad de algunos procesos
- Relacionar los cambios estándar de energía libre con las constantes de equilibrio
Uno de los desafíos de usar la segunda ley de la termodinámica para determinar si una reacción química es espontánea es que debemos determinar el cambio de entropía para el sistema y el cambio de entropía para el entorno. Un segundo reto a la hora de trabajar con una reacción química es que hay que tomar en cuenta la mezcla de las sustancias, cuestión que no ocurre al observar el cambio de fase si es una sustancia pura. Un enfoque alternativo que implica una nueva propiedad termodinámica definida en términos de propiedades del sistema solo fue introducido a finales del siglo XIX por el matemático estadounidense Josiah Willard Gibbs. Esta nueva propiedad se llama la energía libre de Gibbs (\(G\)) (o simplemente la energía libre), y se define en términos de entalpía y entropía de un sistema de la siguiente manera:
\[G=H−TS \nonumber \]
La energía libre es una función de estado, y a temperatura y presión constantes, el cambio de energía libre estándar (ΔG°) puede expresarse de la siguiente manera:
\[ΔG^º_\ce{sys}=ΔH^º_\ce{sys}−TΔS^º_\ce{sys} \nonumber \]
(En aras de la simplicidad, en lo sucesivo se omitirá el subíndice “sys”). Podemos entender la relación entre esta propiedad del sistema y la espontaneidad de un proceso recordando la expresión de la segunda ley previamente derivada:
\[ΔS_\ce{univ}=ΔS+\dfrac{q_\ce{surr}}{T} \nonumber \]
La primera ley lo exige\(q_{surr} = −q_{sys}\), y a presión constante\(q_{sys} = ΔH\), por lo que esta expresión puede ser reescrita de la siguiente manera:
\[ΔS_\ce{univ}=ΔS−\dfrac{ΔH}{T} \nonumber \]
ΔH es el cambio de entalpía del sistema. Al multiplicar ambos lados de esta ecuación por −T, y reorganizar se obtiene lo siguiente:
\[−TΔS_\ce{univ}=ΔH−TΔS \nonumber \]
Al comparar esta ecuación con la anterior para el cambio de energía libre se muestra la siguiente relación:
\[ΔG=−TΔS_\ce{univ} \label{6} \]
El cambio de energía libre es, por lo tanto, un indicador confiable de la espontaneidad de un proceso, estando directamente relacionado con el indicador de espontaneidad previamente identificado,\(ΔS_{univ}\). Cuadro\(\PageIndex{1}\) resume la relación entre la espontaneidad de un proceso y los signos aritméticos de estos indicadores.
| \(ΔS_{univ} > 0\) | Δ G < 0 | se mueve espontáneamente en la dirección hacia adelante, como está escrito, para alcanzar el equilibrio |
| \(ΔS_{univ} < 0\) | Δ G > 0 |
no espontáneo en la dirección hacia adelante, como está escrito, sino que se mueve espontáneamente en la dirección inversa, como está escrito, para alcanzar el equilibrio |
| \(ΔS_{univ} = 0\) | Δ G = 0 | reversible (en equilibrio) |
Cálculo de Cambio de Energía Libre
La energía libre es una función de estado, por lo que su valor depende únicamente de las condiciones de los estados inicial y final del sistema que han sufrido algún cambio. Un enfoque conveniente y común para el cálculo de los cambios de energía libre para cambios físicos y reacciones químicas es mediante el uso de compilaciones ampliamente disponibles de datos termodinámicos de estado estándar. Un método implica el uso de entalpías y entropías estándar para calcular los cambios estándar de energía libre de acuerdo con la siguiente relación como se demuestra en el Ejemplo\(\PageIndex{1}\).
\[ ΔG°=ΔH°−TΔS° \label{7} \]
Es importante entender que para los cambios de fase,\(\Delta G^º\) te dice si el cambio de fase es espontáneo o no; sucederá, o no sucederá. Para las reacciones químicas, te\(\Delta G^º\) dice el alcance de una reacción. En otras palabras,\(\Delta G^º\) para una reacción te dice cuánto producto estará presente en equilibrio. Una reacción con\(\Delta G^º\) < 0 se considera favorecida por el producto en equilibrio; habrá más productos que reactivos cuando la reacción alcance el equilibrio. Una reacción con\(\Delta G^º\) > 0 se considera favorecida por el reactivo en equilibrio; habrá más reactivos que productos cuando la reacción alcance el equilibrio.
Utilice los datos estándar de entalpía y entropía de las Tablas T1 o T2 para calcular el cambio de energía libre estándar para la vaporización del agua a temperatura ambiente (298 K). ¿Qué dice el valor calculado para ΔG° sobre la espontaneidad de este cambio físico para una sustancia pura?
Solución
El proceso de interés es el siguiente:
\[\ce{H2O}(l)⟶\ce{H2O}(g) \label{\(\PageIndex{8}\)} \]
El cambio estándar en la energía libre puede calcularse usando la siguiente ecuación:
\[ΔG^\circ_{298}=ΔH°−TΔS° \label{\(\PageIndex{9}\)} \]
De las Tablas T1 o T2, aquí están los datos:
| Sustancia | \(ΔH^\circ_\ce{f}\ce{(kJ/mol)}\) | \(S^\circ_{298}\textrm{(J/K⋅mol)}\) |
|---|---|---|
| H 2 O (l) | \ (ΔH^\ circ_\ ce {f}\ ce {(kJ/mol)}\)” style="text-align:center; ">−286.83 | \ (S^\ circ_ {298}\ textrm {(J/kmol)}\)” style="text-align:center; ">70.0 |
| H 2 O (g) | \ (ΔH^\ circ_\ ce {f}\ ce {(kJ/mol)}\)” style="text-align:center; ">−241.82 | \ (S^\ circ_ {298}\ textrm {(J/kmol)}\)” style="text-align:center; ">188.8 |
Combinando a 298 K:
\[\begin{align*} ΔH°&=ΔH^\circ_{298}=ΔH^\circ_\ce{f}(\ce{H2O}(g))−ΔH^\circ_\ce{f}(\ce{H2O}(l)) \\[4pt] &=[−241.82\: kJ−(−285.83)]\:kJ/mol \\[4pt] &=44.01\: kJ/mol \\[4pt] ΔS° &=ΔS^\circ_{298}=S^\circ_{298}(\ce{H2O}(g))−S^\circ_{298}(\ce{H2O}(l)) \\[4pt] &=188.8\:J/mol⋅K−70.0\:J/K \\[4pt] &=118.8\:J/mol⋅K \end{align*} \nonumber \]
luego usa Ecuación\ ref {7}:
\[ΔG°=ΔH°−TΔS° \nonumber \]
Convirtiendo todo en kJ y combinando a 298 K:
\[\begin{align*}ΔG^\circ_{298} &=ΔH°−TΔS° \\[4pt] &=44.01\: kJ/mol−(298\: K×118.8\:J/mol⋅K)×\dfrac{1\: kJ}{1000\: J} \end{align*} \nonumber \]
\[\mathrm{44.01\: kJ/mol−35.4\: kJ/mol=8.6\: kJ/mol} \nonumber \]
A 298 K (25 °C)\(ΔG^\circ_{298}>0\), por lo que la ebullición es no espontánea (no espontánea) a 298 K.
Utilice los datos estándar de entalpía y entropía de las Tablas T1 o T2 para calcular el cambio estándar de energía libre para la reacción que se muestra aquí (298 K). ¿Qué dice el valor calculado para ΔG° sobre el alcance de esta reacción a 298 K?
\[\ce{C2H6}(g)⟶\ce{H2}(g)+\ce{C2H4}(g) \nonumber \]
- Responder
-
\(ΔG^\circ_{298}=\mathrm{102.0\: kJ/mol}\); la reacción es favorecida por el reactivo en equilibrio a 25 °C; habrá\(\ce{C2H6}(g)\) más de\(\ce{H2}(g)\) y\(\ce{C2H4}(g) \) en equilibrio
Los cambios de energía libre también pueden utilizar la energía libre estándar de formación\( (ΔG^\circ_\ce{f})\), para cada uno de los reactivos y productos involucrados en la reacción. La energía libre estándar de formación es el cambio de energía libre que acompaña a la formación de un mol de una sustancia a partir de sus elementos en sus estados estándar. Similar a las entalpías estándar de formación,\( (ΔG^\circ_\ce{f})\) es por definición cero para sustancias elementales bajo condiciones de estado estándar. El enfoque para computar el cambio de energía libre para una reacción usando este enfoque es el mismo que se demostró anteriormente para los cambios de entalpía y entropía. Para la reacción
\[m\ce{A}+n\ce{B}⟶x\ce{C}+y\ce{D}, \nonumber \]
el cambio de energía libre estándar a temperatura ambiente puede calcularse como
\[ \begin{align} ΔG^\circ_{298}&=ΔG° \\[4pt] &=∑νΔG^\circ_{298}(\ce{products})−∑νΔG^\circ_{298}(\ce{reactants})\\[4pt] &=[xΔG^\circ_\ce{f}(\ce{C})+yΔG^\circ_\ce{f}(\ce{D})]−[mΔG^\circ_\ce{f}(\ce{A})+nΔG^\circ_\ce{f}(\ce{B})]. \end{align} \nonumber \]
Considerar la descomposición del óxido de mercurio amarillo (II).
\[\ce{HgO}(s,\,\ce{yellow})⟶\ce{Hg}(l)+ \ce{ 1/2 O2(g)} \nonumber \]
Calcular el cambio de energía libre estándar a temperatura ambiente,\(ΔG^\circ_{298}\), usando:
- energías libres estándar de formación y
- entalpías estándar de formación y entropías estándar.
¿Los resultados indican que la reacción es favorecida por el producto o favorecida por el reactivo en el equilibrio?
Solución
Los datos requeridos están disponibles en las Tablas T1 o T2 y se muestran aquí.
| Compuesto | \(ΔG^\circ_\ce{f}\:\mathrm{(kJ/mol)}\) | \(ΔH^\circ_\ce{f}\:\mathrm{(kJ/mol)}\) | \(S^\circ_{298}\:\textrm{(J/K⋅mol)}\) |
|---|---|---|---|
| HgO (s, amarillo) | \ (ΔG^\ circ_\ ce {f}\:\ mathrm {(kJ/mol)}\)” style="text-align:center; ">−58.43 | \ (ΔH^\ circ_\ ce {f}\:\ mathrm {(kJ/mol)}\)” style="text-align:center; ">−90.46 | \ (S^\ circ_ {298}\:\ textrm {(J/kmol)}\)” style="text-align:center; ">71.13 |
| Hg (l) | \ (ΔG^\ circ_\ ce {f}\:\ mathrm {(kJ/mol)}\)” style="text-align:center; ">0 | \ (ΔH^\ circ_\ ce {f}\:\ mathrm {(kJ/mol)}\)” style="text-align:center; ">0 | \ (S^\ circ_ {298}\:\ textrm {(J/kmol)}\)” style="text-align:center; ">75.9 |
| O 2 (g) | \ (ΔG^\ circ_\ ce {f}\:\ mathrm {(kJ/mol)}\)” style="text-align:center; ">0 | \ (ΔH^\ circ_\ ce {f}\:\ mathrm {(kJ/mol)}\)” style="text-align:center; ">0 | \ (S^\ circ_ {298}\:\ textrm {(J/kmol)}\)” style="text-align:center; ">205.2 |
a) Utilizando energías libres de formación:
\[ \begin{align*} ΔG^\circ_{298}&=∑νGS^\circ_{298}(\ce{products})−∑νΔG^\circ_{298}(\ce{reactants}) \\[4pt] &=\left[1ΔG^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔG^\circ_{298}\ce{O2}(g)\right]−1ΔG^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \\[4pt] & \mathrm{=\left[1\:mol(0\: kJ/mol)+\dfrac{1}{2}mol(0\: kJ/mol)\right]−1\: mol(−58.43\: kJ/mol)=58.43\: kJ/mol} \end{align*} \nonumber \]
b) Utilizando entalpías y entropías de formación:
\[\begin{align*}ΔH^\circ_{298}&=∑νΔH^\circ_{298}(\ce{products})−∑νΔH^\circ_{298}(\ce{reactants}) \\[4pt] &=\left[1ΔH^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔH^\circ_{298}\ce{O2}(g)\right]−1ΔH^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \\[4pt] &\mathrm{=[1\: mol(0\: kJ/mol)+\dfrac{1}{2}mol(0\: kJ/mol)]−1\: mol(−90.46\: kJ/mol)=90.46\: kJ/mol} \\[4pt] ΔS^\circ_{298} &=∑νΔS^\circ_{298}(\ce{products})−∑νΔS^\circ_{298}(\ce{reactants}) \\[4pt] &=\left[1ΔS^\circ_{298}\ce{Hg}(l)+\dfrac{1}{2}ΔS^\circ_{298}\ce{O2}(g)\right]−1ΔS^\circ_{298}\ce{HgO}(s,\,\ce{yellow}) \\[4pt] & \mathrm{=\left[1\: mol(75.9\: J/mol\: K)+\dfrac{1}{2}mol(205.2\: J/mol\: K)\right]−1\: mol(71.13\: J/mol\: K)=107.4\: J/mol\: K} \end{align*} \nonumber \]
entonces podemos usar la ecuación\ ref7} directamente:
\[\begin{align*}ΔG°&=ΔH°−TΔS°\\[4pt] &=\mathrm{90.46\: kJ−298.15\: K×107.4\: J/K⋅mol×\dfrac{1\: kJ}{1000\: J}} \\[4pt] &=\mathrm{(90.46−32.01)\:kJ/mol=58.45\: kJ/mol} \end{align*} \nonumber \]
Ambas formas de calcular el cambio estándar de energía libre a 25 °C dan el mismo valor numérico (a tres cifras significativas), y ambas predicen que el proceso es favorecido por reactivos en equilibrio a temperatura ambiente.
Calcular ΔG° utilizando (a) energías libres de formación y (b) entalpías de formación y entropías (Tablas T1 o T2). ¿Los resultados indican que la reacción es favorecida por el producto o favorecida por el reactivo en equilibrio a 25 °C?
\[\ce{C2H4}(g)⟶\ce{H2}(g)+\ce{C2H2}(g) \nonumber \]
- Responder
-
141.5 kJ/mol, favorecido por reactivo en equilibrio
Dependencia de la temperatura de la espontaneidad y grado de reacción
Como se demostró anteriormente en la sección de entropía de este capítulo, la espontaneidad de un proceso puede depender de la temperatura del sistema. Las transiciones de fase, por ejemplo, procederán espontáneamente en una dirección u otra dependiendo de la temperatura de la sustancia en cuestión. De manera similar, pero no idéntica, algunas reacciones químicas pueden pasar de ser favorecidas por el producto en equilibrio, a ser favorecidas por el reactivo en equilibrio, dependiendo de la temperatura.
El valor numérico\(\Delta G^º\) de siempre depende de la temperatura. En esta sección estamos determinando si el signo de\(\Delta G^º\) depende o no de la temperatura.
Para ilustrar este concepto, se considera la ecuación que relaciona el cambio de energía libre con los cambios de entalpía y entropía para el proceso:
\[ ΔG^º=ΔH^º−TΔS^º \nonumber \]
La extensión de un proceso, como se refleja en el signo aritmético de su cambio estándar de energía libre, se determina entonces por los signos de los cambios de entalpía y entropía y, en algunos casos, la temperatura absoluta. Dado que T es la temperatura absoluta (Kelvin), solo puede tener valores positivos. Por lo tanto, existen cuatro posibilidades con respecto a los signos de los cambios de entalpía y entropía:
- Tanto Δ H º como Δ S º son positivos. Esta condición describe un proceso endotérmico que implica un aumento en la entropía del sistema. En este caso, Δ G º será negativo si la magnitud del término T Δ S º es mayor que Δ H º. Si el término T Δ S º es menor que Δ H º, el cambio de energía libre será positivo. Tal proceso es favorecido por el producto en equilibrio a altas temperaturas y el reactivo favorecido en equilibrio a bajas temperaturas.
- Tanto Δ H º como Δ S º son negativos. Esta condición describe un proceso exotérmico que implica una disminución de la entropía del sistema. En este caso, Δ G º será negativo si la magnitud del término T Δ S º es menor que Δ H º. Si la magnitud del término T Δ S º es mayor que Δ H º, el cambio de energía libre será positivo. Tal proceso es favorecido por el producto en equilibrio a bajas temperaturas y el reactivo favorecido en equilibrio a altas temperaturas.
- Δ H º es positivo y Δ S º es negativo. Esta condición describe un proceso endotérmico que implica una disminución de la entropía del sistema. En este caso, Δ G º será positivo independientemente de la temperatura. Tal proceso es favorecido por reactivos en equilibrio a todas las temperaturas.
- Δ H º es negativo y Δ S º es positivo. Esta condición describe un proceso exotérmico que implica un aumento en la entropía del sistema. En este caso, Δ G º será negativo independientemente de la temperatura. Tal proceso es favorecido por el producto en equilibrio a todas las temperaturas.
Estos cuatro escenarios se resumen en la Tabla\(\PageIndex{1}\)
|
Signo de\(\Delta H^o\) |
Signo de\(\Delta S^o\) |
Signo de\(\Delta G^o\) |
Dependencia de temperatura de\(\Delta G^o\) |
|---|---|---|---|
| \ (\ Delta H^o\) ">- | \ (\ Delta S^O\) ">+ | \ (\ Delta G^O\) ">- | \ (\ Delta g^O\) ">El signo de\(\Delta G^o\) no depende de la temperatura.La reacción es favorecida por el producto en equilibrio a todas las temperaturas. |
| \ (\ Delta H^O\) ">+ | \ (\ Delta S^O\) ">- | \ (\ Delta G^O\) ">+ | \ (\ Delta g^O\) ">El signo de\(\Delta G^o\) no depende de la temperatura.La reacción es favorecida por el reactivo en equilibrio a todas las temperaturas. |
| \ (\ Delta H^o\) ">- | \ (\ Delta S^O\) ">- | \ (\ Delta G^o\) ">- o + | \ (\ Delta G^o\) ">El signo de\(\Delta G^o\) sí depende de la temperatura. La reacción se verá favorecida por el producto en equilibrio a temperaturas más bajas. |
| \ (\ Delta H^O\) ">+ | \ (\ Delta S^O\) ">+ | \ (\ Delta G^o\) ">- o + | \ (\ Delta G^O\) ">
El signo de\(\Delta G^o\) sí depende de la temperatura. La reacción se verá favorecida por el producto en equilibrio a temperaturas más bajas. |
La combustión incompleta del carbono se describe mediante la siguiente ecuación:
\[\ce{2C}(s)+\ce{O2}(g)⟶\ce{2CO}(g) \nonumber \]
¿El signo\(\Delta G^º\) de este proceso depende de la temperatura?
Solución
Los procesos de combustión son exotérmicos (\(ΔH^º < 0\)). Esta reacción particular implica un incremento en la entropía debido al incremento acompañante en la cantidad de especies gaseosas (ganancia neta de un mol de gas,\(ΔS^º > 0\)). Por lo tanto, la reacción se ve favorecida por el producto en equilibrio (\(ΔG^º < 0\)) a todas las temperaturas.
Los calentadores de manos químicos populares generan calor por la oxidación del hierro al aire:
\[\ce{4Fe}(s)+\ce{3O2}(g)⟶\ce{2Fe2O3}(s) \nonumber \]
¿El signo\(\Delta G^o\) de este proceso depende de la temperatura?
- Responder
-
Δ H º y Δ S º son ambos negativos; la reacción es favorecida por el producto en equilibrio a bajas temperaturas.
Al considerar las conclusiones extraídas respecto a la dependencia de la temperatura del signo de Δ G º, es importante tener en cuenta qué significan los términos “alto” y “bajo”. Dado que estos términos son adjetivos, las temperaturas en cuestión se consideran altas o bajas en relación con alguna temperatura de referencia. Un proceso que está favorecido por reactivo en equilibrio a una temperatura pero favorecido por el producto en equilibrio a otra temperatura necesariamente sufrirá un cambio en “extensión” (como se refleja en su Δ G º) a medida que la temperatura varía. Esto se ilustra claramente mediante una presentación gráfica de la ecuación de cambio de energía libre, en la que Δ G º se traza en el eje y versus T en el eje x:
\[ΔG^º=ΔH^º−TΔS^º \nonumber \]
\[y=b+mx \nonumber \]
Tal gráfica se muestra en la Figura\(\PageIndex{2}\). Un proceso cuyos cambios de entalpía y entropía son del mismo signo aritmético exhibirá una dependencia de la temperatura para el signo de Δ G º como lo representan las dos líneas amarillas en la gráfica. Cada línea cruza de un dominio de espontaneidad (positivo o negativo Δ G º) al otro a una temperatura que es característica del proceso en cuestión. Esta temperatura está representada por la intercepción x de la línea, es decir, el valor de T para el cual Δ G º es cero:
\[ΔG^º=0=ΔH^º−TΔS^º \nonumber \]
\[T=\dfrac{ΔH^º}{ΔS^º} \nonumber \]
Así, decir que un proceso es favorecido por el producto en equilibrio a temperaturas “altas” o “bajas” significa que la temperatura está por encima o por debajo, respectivamente, esa temperatura a la que Δ G º para el proceso es cero.
En esta discusión, hemos utilizado dos descripciones diferentes para el significado del signo de Δ G º. Debes estar al tanto del significado de cada descripción.
a) Grado de Reacción: Esta descripción se utiliza para predecir la relación entre las concentraciones de producto y reactivo en equilibrio. En esta descripción, utilizamos el término termodinámico Δ G º para decirnos la misma información que la constante de equilibrio, K. Cuando Δ G º < 0, K > 1, y la reacción será favorecida por el producto en equilibrio. Cuando Δ G º > 0, K< 1, y la reacción se ve favorecida por el reactivo en equilibrio. Cuando Δ G º = 0, K =1, y la reacción tendrá cantidades aproximadamente iguales de productos y reactivos en equilibrio. En todos los casos, la reacción formará una mezcla de productos y reactivos en equilibrio. Utilizamos el signo y magnitud de Δ G º para decirnos cuánto producto se elaborará si se permite que la reacción alcance el equilibrio.
b) Espontaneidad: Esta descripción es mucho más complicada porque implica dos interpretaciones diferentes de cómo ocurre una reacción en estado estándar. Una interpretación implica el proceso hipotético en el que la reacción transcurre desde un punto de partida de reactivos puros hasta un punto de acabado de productos puros, con todas las sustancias aisladas en sus propios contenedores bajo condiciones de estado estándar. En la segunda interpretación, más realista, la reacción comienza con todos los reactivos y todos los productos en su estado estándar en un contenedor. Luego permitimos que esta mezcla específica reaccione una cantidad infinitesimalmente pequeña para que podamos obtener una tasa de cambio en la energía libre con respecto al grado de reacción cuando todos los reactivos y productos se mezclan y (esencialmente) en sus estados estándar. Si bien cada interpretación describe un escenario de reacción diferente, el valor de la diferencia en la energía libre y el valor de la tasa de cambio en la energía libre son el mismo número. Si Δ G º < 0, decimos que la reacción es espontánea, es decir, que la reacción procedería en la dirección hacia adelante, como está escrito, para formar productos puros en su estado estándar. Si Δ G º > 0, decimos que la reacción es no espontánea, lo que significa que la reacción procedería en sentido inverso, como está escrito, para formar reactivos puros en su estado estándar. Si Δ G º = 0, decimos que ni los reactivos ni los productos son favorecidos para formarse.
Un tratamiento detallado del significado de δGº se puede encontrar en el artículo, “Energía libre versus extensión de reacción” de Richard S. Treptow, Journal of Chemical Education, 1996, Volumen 73 (1), 51-54.
Como se define en el capítulo sobre líquidos y sólidos, el punto de ebullición de un líquido es la temperatura a la que sus fases sólida y líquida están en equilibrio (es decir, cuando la vaporización y condensación ocurren a tasas iguales). Utilice la información de las Tablas T1 o T2 para estimar el punto de ebullición del agua.
Solución
El proceso de interés es el siguiente cambio de fase:
Cuando este proceso está en equilibrio, Δ G = 0, por lo que es cierto lo siguiente:
\[0=ΔH°−TΔS°\hspace{40px}\ce{or}\hspace{40px}T=\dfrac{ΔH°}{ΔS°} \nonumber \]
Utilizando los datos termodinámicos estándar de las Tablas T1 o T2,
\ [\ begin {align*}
ΔH°&=ΔH^\ circ_\ ce {f} (\ ce {H2O} (g)) −ΔH^\ circ_\ ce {f} (\ ce {H2O} (l))\ nonumber\\
&=\ mathrm {−241.82\: kJ/mol− (−285.83\: kJ/mol) =44.01\: KJ/mol}\ nonumber
\ end {align*}\ nonumber\]
\ [\ begin {alinear*}
ΔS°&=ΔS^\ circ_ {298} (\ ce {H2O} (g)) −ΔS^\ circ_ {298} (\ ce {H2O} (l))\ nonumber\\
&=\ mathrm {188.8\: J/kmol−70.0\: J/kmol}\ nonumber
\ end {align*}\ nonumber\]
\[T=\dfrac{ΔH°}{ΔS°}=\mathrm{\dfrac{44.01×10^3\:J/mol}{118.8\:J/K⋅mol}=370.5\:K=97.3\:°C} \nonumber \]
El valor aceptado para el punto de ebullición normal del agua es 373.2 K (100.0 °C), por lo que este cálculo está de acuerdo razonable. Obsérvese que los valores para los datos de entalpía y entropía utilizados se derivaron de datos estándar a 298 K (Tablas T1 o T2.). Si lo desea, podría obtener resultados más precisos mediante el uso de cambios de entalpía y entropía determinados en (o al menos más cerca de) el punto de ebullición real.
Utilice la información de las Tablas T1 o T2 para estimar el punto de ebullición de CS 2.
- Responder
-
313 K (valor aceptado 319 K).
Energía Libre y Equilibrio
El cambio de energía libre para un proceso puede ser visto como una medida de su fuerza impulsora. Un valor negativo para Δ G representa una fuerza motriz finita para el proceso en la dirección hacia adelante, mientras que un valor positivo representa una fuerza impulsora para el proceso en la dirección inversa. Cuando Δ G es cero, las fuerzas impulsoras hacia adelante y hacia atrás son iguales, por lo que el proceso ocurre en ambas direcciones a la misma velocidad (el sistema está en equilibrio).
En el capítulo sobre equilibrio se introdujo el cociente de reacción, Q, como una medida conveniente del estado de un sistema de equilibrio. Recordemos que Q es el valor numérico de la expresión de acción masiva para el sistema, y que puede usar su valor para identificar la dirección en la que procederá una reacción con el fin de lograr el equilibrio. Cuando Q es menor que la constante de equilibrio, K, la reacción procederá en la dirección de avance hasta alcanzar el equilibrio y Q = K. Por el contrario, si Q > K, el proceso procederá en sentido inverso hasta lograr el equilibrio.
El cambio de energía libre para un proceso que tiene lugar con reactivos y productos presentes en condiciones no estándar, Δ G, está relacionado con el cambio de energía libre estándar, Δ G°, de acuerdo con esta ecuación:
\[ΔG=ΔG°+RT\ln Q \label{eq10A} \]
R es la constante del gas (8.314 J/K mol), T es el kelvin o temperatura absoluta, y Q es el cociente de reacción. Podemos usar esta ecuación para predecir la espontaneidad de un proceso bajo cualquier conjunto dado de condiciones como se ilustra en Ejemplo\(\PageIndex{1}\).
¿Cuál es el cambio de energía libre para el proceso que se muestra aquí bajo las condiciones especificadas?
T = 25 °C,\(P_{\ce{N2}}=\mathrm{0.870\: atm}\),\(P_{\ce{H2}}=\mathrm{0.250\: atm}\), y\(P_{\ce{NH3}}=\mathrm{12.9\: atm}\)
\[\ce{2NH3}(g)⟶\ce{3H2}(g)+\ce{N2}(g) \hspace{20px} ΔG°=\mathrm{33.0\: kJ/mol} \nonumber \]
S olución
La ecuación\ ref {EQ10a} relaciona el cambio de energía libre con el cambio de energía libre estándar y el cociente de reacción y puede usarse directamente:
\[\begin{align*} ΔG&=ΔG°+RT\ln Q \\[4pt] &=\mathrm{33.0\:\dfrac{kJ}{mol}+\left(8.314\:\dfrac{J}{mol\: K}×298\: K×\ln\dfrac{(0.250^3)×0.870}{12.9^2}\right)}\\[4pt] &=\mathrm{9680\:\dfrac{J}{mol}\:or\: 9.68\: kJ/mol} \end{align*} \nonumber \]
Dado que el valor calculado para Δ G es positivo, la reacción es no espontánea bajo estas condiciones. La reacción procederá en sentido inverso para alcanzar el equilibrio.
Calcular el cambio de energía libre para esta misma reacción a 875 °C en una mezcla de 5.00 L que contiene 0.100 mol de cada gas. ¿La reacción es espontánea bajo estas condiciones?
- Responder
-
Δ G = −47 kJ; sí, la reacción procede en la dirección hacia adelante, como está escrito, para alcanzar el equilibrio.
Para un sistema en equilibrio, Q = K y Δ G = 0, y la Ecuación\ ref {EQ10a} puede escribirse como
\[ \underbrace{0=ΔG°+RT\ln K}_{\text{at equilibrium}} \nonumber \]
\[ΔG°=−RT\ln K \label{eq4A} \]
o alternativamente
\[K=e^{−\frac{ΔG°}{RT}} \label{eq4B} \]
Esta forma de la ecuación proporciona un vínculo útil entre estas dos propiedades termodinámicas esenciales, y puede ser utilizada para derivar constantes de equilibrio a partir de cambios estándar de energía libre y viceversa. Las relaciones entre los cambios estándar de energía libre y las constantes de equilibrio se resumen en la Tabla\(\PageIndex{1}\).
| K | ΔG° | Comentarios |
|---|---|---|
| < 1 | > 0 | Los reactivos son más abundantes en equilibrio. |
| = 1 | = 0 | Los reactivos y productos son igualmente abundantes en equilibrio. |
| > 1 | < 0 | Los productos son más abundantes en equilibrio. |
Dado que las energías libres estándar de formación de Ag + (aq), Cl − (aq) y AgCl (s) son 77.1 kJ/mol, −131.2 kJ/mol, y −109.8 kJ/mol, respectivamente, se calcula el producto de solubilidad, K sp, para AgCl.
Solución
La reacción de interés es la siguiente:
\[\ce{AgCl}(s)⇌\ce{Ag+}(aq)+\ce{Cl-}(aq) \hspace{20px} K_\ce{sp}=\ce{[Ag+][Cl- ]} \nonumber \]
El cambio estándar de energía libre para esta reacción se calcula primero usando energías libres estándar de formación para sus reactivos y productos:
\[ \begin{align*} ΔG° =ΔG^\circ_{298} &=[ΔG^\circ_\ce{f}(\ce{Ag+}(aq))+ΔG^\circ_\ce{f}(\ce{Cl-}(aq))]−[ΔG^\circ_\ce{f}(\ce{AgCl}(s))] \\[4pt] &=[77.1\: kJ/mol−131.2\: kJ/mol]−[−109.8\: kJ/mol] \\[4pt] &=55.7\: kJ/mol \end{align*} \nonumber \]
La constante de equilibrio para la reacción puede entonces derivarse de su cambio de energía libre estándar a través de la Ecuación\ ref {EQ4b}:
\[\begin{align*} K_\ce{sp}&=e^{−\dfrac{ΔG°}{RT}}=\exp\left(−\dfrac{ΔG°}{RT}\right) \\[4pt] &=\mathrm{\exp\left(−\dfrac{55.7×10^3\:J/mol}{8.314\:J/mol⋅K×298.15\:K}\right)}\\&=\mathrm{\exp(−22.470)=e^{−22.470}=1.74×10^{−10}} \end{align*} \nonumber \]
Utilizar los datos termodinámicos proporcionados en las Tablas T1 o T2 para calcular la constante de equilibrio para la disociación del tetroóxido de dinitrógeno a 25 °C.
\[\ce{NO}_{2(g)} \rightleftharpoons \ce{N_2O}_{4(g)} \nonumber \]
- Responder
-
K = 6.9
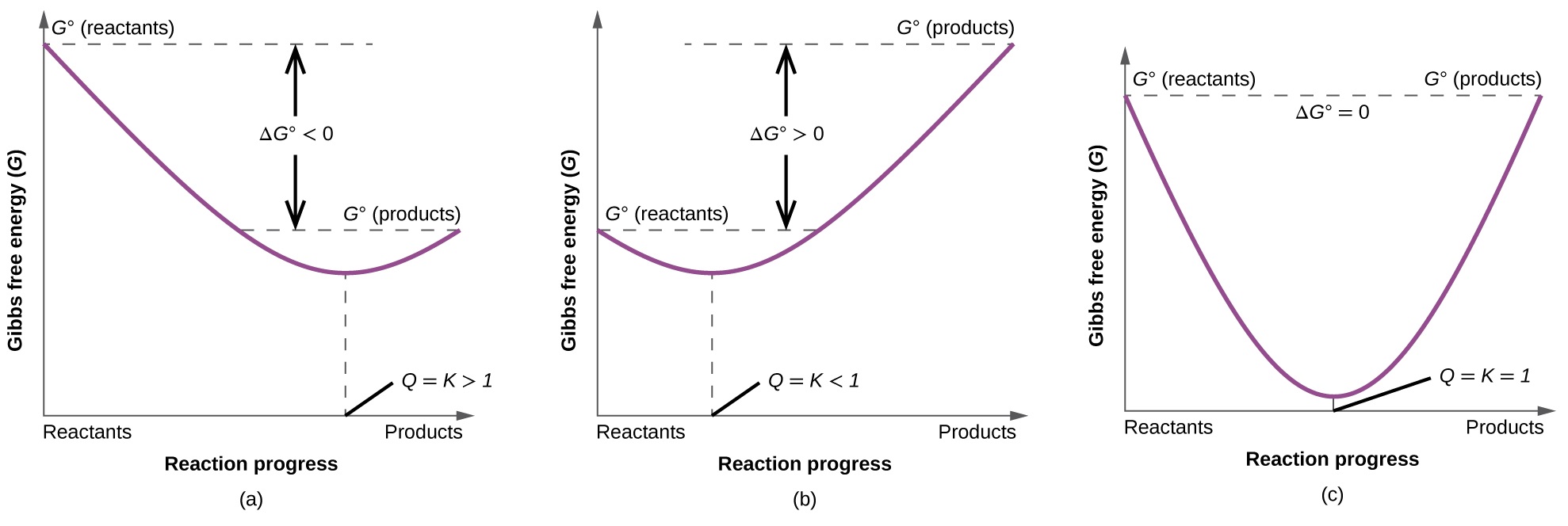
Para ilustrar mejor la relación entre estos dos conceptos termodinámicos esenciales, considere la observación de que las reacciones proceden espontáneamente en una dirección que finalmente establece el equilibrio. Como se puede mostrar graficando el cambio de energía libre frente a la extensión de la reacción (por ejemplo, como se refleja en el valor de Q), el equilibrio se establece cuando se minimiza la energía libre del sistema (Figura\(\PageIndex{3}\)). Si un sistema está presente con reactivos y productos presentes en cantidades de no equilibrio (Q ≠ K), la reacción procederá espontáneamente en la dirección necesaria para establecer el equilibrio.
Resumen
La energía libre de Gibbs (G) es una función de estado definida solo con respecto a las cantidades del sistema y puede usarse para predecir la espontaneidad de un proceso. Un valor negativo para Δ G indica que el proceso procederá en la dirección hacia adelante para alcanzar el equilibrio; un Δ G positivo indica que el proceso procederá en la dirección inversa para alcanzar el equilibrio; y un Δ G de cero indica que el sistema está en equilibrio. Un valor negativo para Δ G º significa que la reacción es favorecida por el producto en equilibrio. Un valor positivo para Δ G º significa que la reacción está favorecida por el reactivo en equilibrio. Si Δ G º es igual a 0 (una ocurrencia rara), la reacción tiene cantidades aproximadamente iguales de reactivos y productos en equilibrio.Una serie de enfoques para el cálculo de los cambios de energía libre son posibles.
Ecuaciones Clave
- Δ G = Δ H − T Δ S
- Δ G = Δ G° + RT ln Q
- Δ G° = − RT ln K
Glosario
- Cambio de energía libre de Gibbs (G)
- propiedad termodinámica definida en términos de entalpía y entropía del sistema; todos los procesos espontáneos implican una disminución de G
- cambio de energía libre estándar (Δ G°)
- cambio en la energía libre para un proceso que ocurre en condiciones estándar (presión de 1 bar para gases, concentración de 1 M para soluciones)
- energía libre estándar de formación\( (ΔG^\circ_\ce{f})\)
- cambio en la energía libre que acompaña a la formación de un mol de sustancia a partir de sus elementos en sus estados estándar


