1.9: Difusión

1. DIFUSIÓN

A cualquier temperatura diferente del cero absoluto todos los átomos, independientemente de su estado de agregación (gaseoso, líquido o sólido), están en constante movimiento. Dado que el movimiento de las partículas está asociado con colisiones, el camino de una sola partícula es uno en zigzag. Sin embargo, una agregación de partículas “difusoras” tiene una deriva observable de lugares de mayor a lugares de menor concentración (fig. 1). Por esta razón la difusión se conoce como un fenómeno de transporte.

Figura 1 Transporte masivo, difusión como consecuencia de las diferencias espaciales existentes en la concentración.

En cada reacción de difusión (el flujo de calor, por ejemplo, es también un proceso de difusión), el flujo (de materia, calor, electricidad, etc.) sigue la relación general:

Flujo = (conductividad) x (fuerza motriz)

En el caso de la difusión atómica o molecular, la “conductividad” es referida como la difusividad o la constante de difusión, y está representada por el símbolo D. Nos damos cuenta de las consideraciones anteriores que esta constante de difusión (D) refleja la movilidad de las especies difusoras en el ambiente dado y en consecuencia asume valores mayores en gases, más pequeños en líquidos y extremadamente pequeños en sólidos.

Figura 2 Gradiente de concentración (constante) en la dirección x

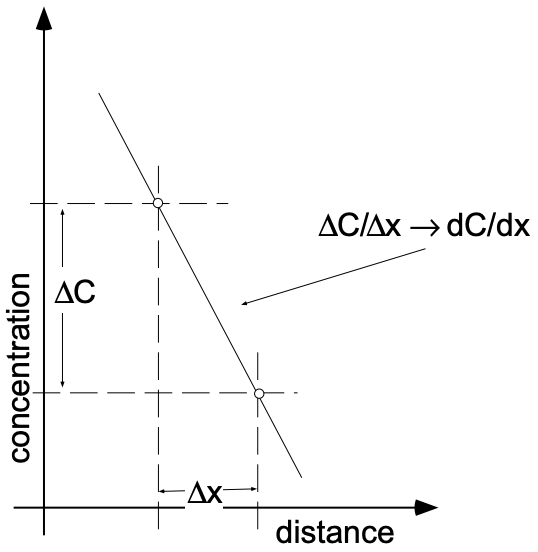
La “fuerza impulsora” para muchos tipos de difusión es la existencia de un gradiente de concentración. El término “gradiente” describe la variación de una propiedad dada en función de la distancia en la dirección x. Si un material presenta una variación lineal de concentración con la distancia en la dirección x, se habla de un gradiente de concentración constante en la dirección x. El gradiente en sí es la tasa de cambio de la concentración con la distancia (dc/dx), que es la misma que la pendiente de una gráfica de concentración vs. posición\(\Delta c/\Delta x)\) (ver fig. 2).

Difusión en estado estacionario y no estable

Los procesos de difusión pueden dividirse en dos tipos: (a) estado estacionario y (b) estado no estacionario. La difusión en estado estacionario tiene lugar a una velocidad constante, es decir, una vez que se inicia el proceso, el número de átomos (o moles) que cruzan una interfaz determinada (el flujo) es constante con el tiempo. Esto significa que en todo el sistema dc/dx = constante y dc/dt = 0.

La difusión en estado no estacionario es un proceso dependiente del tiempo en el que la velocidad de difusión es una función del tiempo. Así dc/dx varía con el tiempo y dc/dt ≠ 0. Ambos tipos de difusión son descritos cuantitativamente por las leyes de difusión de Fick. La primera ley se refiere a la difusión tanto en estado estacionario como en estado no estacionario, mientras que la segunda ley se ocupa únicamente de la difusión en estado no estacionario.

2. DIFUSIÓN EN ESTADO ESTACIONARIO (PRIMERA LEY DE FICK)

Con base en las consideraciones anteriores, la Primera Ley de Fick podrá formularse de la siguiente manera:

\(\mathrm{J}=-\mathrm{D}\left(\dfrac{\mathrm{dc}}{\mathrm{dx}}\right)\)En palabras: El flujo difusivo es proporcional al gradiente de concentración existente.

El signo negativo en esta relación indica que el flujo de partículas se produce en una dirección de gradiente “hacia abajo”, es decir, de regiones de mayor a regiones de menor concentración. El flujo se\(\mathrm{J}\) puede dar en unidades de átomos\(/ \mathrm{cm}^2 \mathrm{~s}\), moles/\(\mathrm{cm}^2 \mathrm{~s}\), o equivalentes. Correspondientemente, la difusividad (D) asumirá las dimensiones\(\mathrm{cm}^2 / \mathrm{s}\), como puede verse a partir de un análisis dimensional:

\(\mathrm{J}\left(\dfrac{\text { moles }}{\mathrm{cm}^2 \mathrm{~s}}\right)=-\mathrm{D}\left(\dfrac{\mathrm{dc}}{\mathrm{dx}}\right)\left(\dfrac{\text { moles } \cdot \mathrm{cm}^{-3}}{\mathrm{~cm}}\right)\)

Así:\(D=\mathrm{cm}^2 / \mathrm{s}\)

Al igual que las reacciones químicas, la difusión es un proceso térmicamente activado y la dependencia de la temperatura de la difusión aparece en la difusividad como una ecuación de “tipo Arrhenius”:

\(D=D_0 e^{-E_a / R T}\)

donde\(D_o\) (el equivalente de\(A\) en la dependencia de temperatura previamente discutida de la constante de velocidad) incluye factores tales como la distancia de salto, la frecuencia vibracional de las especies difusoras, etc. Los valores seleccionados de\(D, D_0\) y\(E_a\) se dan en la Tabla 1 (a) y (b).

CUADRO 1

(a) Valores seleccionados de constantes de difusión (D)

\ begin {aligned}
&\ begin {array} {llrl}
\ subrayado {\ text {Sustancia difusora}} &\ subrayado {\ text {Solvente}} &\ subrayado {T\ left ({} ^ {\ circ}\ mathrm {C}\ right)} &\ subrayado {D\ left (\ mathrm {~cm} ^2\ cdot\ mathrm {s} ^ ^ -1}\ derecha)}\\
\ mathrm {Au} &\ mathrm {Cu} & 400 & 5\ times 10^ {-13}\
\ mathrm {Cu}\ text {(Auto-Difusor)} & (\ mathrm {Cu}) & 650 & 3.2\ times 10^ {-12}\
\ mathrm {C} &\ mathrm {Fe}\ text {(FCC)} & 950 & 10^ {-7}\\ text {Metanol} &
\ mathrm {Fe}\ text {H} _2\ mathrm {O} & amp; 18 & 1.4\ times 10^ {-5}\\
\ mathrm {O} _2 &\ text {Air} & 0 & 0.178\
\ mathrm {H} _2 &\ text {Air} & 0 & 0.611
\ end {array}\
\ end {alineada}

b) Valores seleccionados de\(D_o\) y\(E_a\) para los sistemas de difusión

Soluto	Solvente (estructura hospedadora)	\(\underline{D_o, \mathrm{cm}^2 \mathrm{s}}\)	\(\underline{E_a}\), Kjoules/mole
1. Carbono	hierro fcc	\ (\ subrayado {D_o,\ mathrm {cm} ^2\ mathrm {s}}\) ">0.2100	\ (\ subrayado {e_a}\), kjoules/mole">142
2. Carbono	hierro bcc	\ (\ subrayado {d_O,\ mathrm {cm} ^2\ mathrm {s}}\) ">0.0079	\ (\ subrayado {e_a}\), kjoules/mole">76
3. Hierro	hierro fcc	\ (\ subrayado {D_o,\ mathrm {cm} ^2\ mathrm {s}}\) ">0.5800	\ (\ subrayado {e_a}\), kjoules/mole">185
4. Hierro	hierro bcc	\ (\ subrayado {D_o,\ mathrm {cm} ^2\ mathrm {s}}\) ">5.8000	\ (\ subrayado {e_a}\), kjoules/mole">251
5. Níquel	hierro fcc	\ (\ subrayado {D_o,\ mathrm {cm} ^2\ mathrm {s}}\) ">0.5000	\ (\ subrayado {e_a}\), kjoules/mole">276
6. Manganeso	hierro fcc	\ (\ subrayado {D_o,\ mathrm {cm} ^2\ mathrm {s}}\) ">0.3500	\ (\ subrayado {e_a}\), kjoules/mole">283
7. Zinc	cobre	\ (\ subrayado {d_O,\ mathrm {cm} ^2\ mathrm {s}}\) ">0.0330	\ (\ subrayado {e_a}\), kjoules/mole">159
8. Cobre	aluminio	\ (\ subrayado {D_o,\ mathrm {cm} ^2\ mathrm {s}}\) ">2.0000	\ (\ subrayado {e_a}\), kjoules/mole">142
9. Cobre	cobre	\ (\ subrayado {D_o,\ mathrm {cm} ^2\ mathrm {s}}\) ">11.0000	\ (\ subrayado {e_a}\), kjoules/mole">240
10. Plata	plata	\ (\ subrayado {D_o,\ mathrm {cm} ^2\ mathrm {s}}\) ">0.7200	\ (\ subrayado {e_a}\), kjoules/mole">188

Una aplicación típica de la primera ley de Fick: Determinar la velocidad a la que el helio (He), sostenido a 5 atm y\(200^{\circ} \mathrm{C}\) en una bombilla de vidrio Pyrex de\(50 \mathrm{~cm}\) diámetro y espesor de pared (\(\mathrm{x}\)) de\(0.1 \mathrm{~cm}\), se difunde a través del Pyrex hacia el exterior. Supongamos que la presión fuera del tubo en todo momento sigue siendo insignificante (ver fig. 3). (Para la difusión de gases es

Figura 3 Condiciones para la difusión de He a partir de una bombilla de vidrio.

costumbre, aunque no necesaria, sustituir la constante\(D\) de difusión por la constante de permeación\(\mathrm{K}\), normalmente dada en unidades de\(\mathrm{cm}^2 / \mathrm{s} \cdot\) atm. Usando las leyes de gas,\(\mathrm{K}\) se convierte fácilmente en\(\mathrm{D}\) si así se desea.)

En el presente sistema

\(\mathrm{K}=1 \times 10^{-9} \mathrm{~cm}^2 / \mathrm{s} \cdot \mathrm{atm}\)

Ahora podemos configurar la ecuación de difusión:

\ (J=-\ mathrm {K}\ izquierda (\ frac {\ mathrm {dP}} {\ mathrm {dx}}\ derecha)\ quad\ begin {alineado}
&\ text {(y operar con presiones en su lugar}\\
&\ text {de concentraciones)}
\ end {alineado}\)

Ahora podemos separar formalmente las variables e integrar:

\ begin {alineado}
J\ mathrm {dx} &=-\ mathrm {kDP}\
\ int_ {\ mathrm {x} =0} ^ {\ mathrm {x} =0.1}\ mathrm {Jdx} &=-\ int_ {\ mathrm {p} _2=5} ^ {p_1=0}\ mathrm {kDP}\
\ mathrm {J} &=\ mathrm {K}\ frac {5.0} {0.1}
\ end {alineado}

Podemos renunciar a la integración desde entonces\((\mathrm{dP} / \mathrm{dx})=(\Delta \mathrm{P} / \Delta \mathrm{x})\) y podemos escribir de inmediato:

\ begin {alineado}
\ mathrm {J} (\ text {total}) &=-\ mathrm {K}\ frac {\ Delta\ mathrm {P}} {\ Delta\ mathrm {x}}\ veces\ mathrm {A} =5\ veces 10^ {-8}\ veces 7.9\ veces 10^3\
\ mathrm {~J} &=3.9\ veces 10^ {-4}? ?
\ end {alineado}

Las unidades del flujo pueden obtenerse a partir de un análisis dimensional:

\(\mathrm{J}=-\mathrm{K} \times \dfrac{\Delta \mathrm{P}}{\Delta \mathrm{x}} \times \mathrm{A}=\dfrac{\mathrm{cm}^2}{\mathrm{~s} \cdot \mathrm{atm}} \dfrac{\mathrm{atm}}{\mathrm{cm}} \dfrac{\mathrm{cm}^2}{1}=\dfrac{\mathrm{cm}^3}{\mathrm{~s}}\)

El flujo total es\(3.9 \times 10^{-4} \mathrm{~cm}^3 / \mathrm{s}\) (con el volumen de gas dado para\(0^{\circ} \mathrm{C}\) y\(1 \mathrm{~atm}\)). Si se determinara el flujo total de gas por difusión para un intervalo de tiempo especificado, el volumen se multiplicaría por el tiempo indicado.

3. DIFUSIÓN EN ESTADO NO ESTACIONARIO (SEGUNDA LEY DE FICK)

El tratamiento cuantitativo de los procesos de difusión en estado no estacionario se formula como una ecuación diferencial parcial. Está más allá del alcance de 3.091 tratar las ecuaciones en detalle pero podemos considerar cualitativamente la segunda ley y examinar cuantitativamente algunas soluciones relevantes.

La diferencia entre las condiciones de difusión en estado estacionario y no estacionario se puede visualizar fácilmente (fig. 4). En el primer caso tenemos, por ejemplo, la difusión del gas

Figura 4 Difusión en estado estacionario y en estado no estacionario

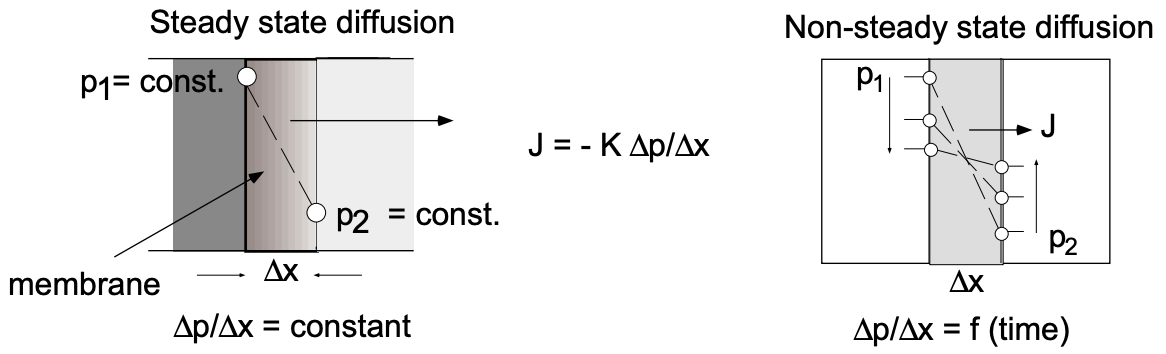
desde un volumen infinito (\(\mathrm{P}_1\)const) a través de una membrana hasta un volumen infinito (\(\mathrm{P}_2\)const). El gradiente de presión a través de la membrana permanece constante al igual que el flujo difusivo. En el segundo caso se trata de la difusión de un volumen finito a través de una membrana a un volumen finito. Las presiones en los depósitos involucrados cambian con el tiempo al igual que, en consecuencia, el gradiente de presión a través de la membrana.

(No está obligado a estar familiarizado con la siguiente derivación de la Ley del Segundo Fick, pero debe conocer su forma final.)

Considere un elemento de volumen (entre x y x+dx de área de sección transversal unitaria) de una membrana que separa dos volúmenes finitos involucrados en un sistema de difusión (fig. 5). El flujo de un material dado en el elemento de volumen menos el flujo fuera del elemento de volumen es igual a la tasa de acumulación del material en este elemento de volumen:

\(J_x-J_{x+d x}=\dfrac{\partial \bar{c}}{\partial t} d x\)

[\(\bar{c}\)es la concentración promedio en el elemento volumen y\(\bar{c} d x\) es la cantidad total del material difusor en el elemento en el tiempo (t).]

Usando una serie Taylor podemos ampliar\(J_{x+d x}\)\(x\) y obtener:

\(J_{x+d x}=J_x+\dfrac{\partial J_x}{\partial x} d x+\dfrac{\partial^2 J_x}{\partial x^2} \dfrac{d x^2}{2}+\ldots\)

En consecuencia, como\(\mathrm{dx} \rightarrow 0\):

\(\dfrac{\partial}{\partial x}\left(D \dfrac{\partial c}{d x}\right)=\dfrac{\partial c}{\partial t}\)

y si\(D\) no varía con\(x\) (que normalmente es el caso) tenemos la formulación de la Segunda Ley de Fick:

\(\dfrac{\partial \mathrm{C}}{\partial \mathrm{t}}=\mathrm{D} \dfrac{\partial^2 \mathrm{C}}{\partial \mathrm{x}^2} \quad \text { (Fick's Second Law) }\)

En términos físicos esta relación establece que la tasa de cambio de composición es proporcional a la “tasa de cambio” del gradiente de concentración más que al gradiente de concentración en sí mismo.

Las soluciones a la segunda ley de Fick dependen de las condiciones límite impuestas por el problema particular de interés. Como ejemplo, consideremos el siguiente problema (encontrado en muchos procesos de estado sólido):

Una situación frecuente es la difusión de un componente 2 en una región infinita de un material 1 (fig. 6) [difusión plana de elementos dopantes en semiconductores

Figura 6 Difusión a concentración superficial constante; la concentración aparente del componente 2 al inicio de la difusión es\(c_2^{\prime}\) (en a) y es cero (en b).

para la generación de dispositivos de unión (uniones p-n, transistores de unión)]. Las condiciones límite son: la concentración del componente (2) en la superficie de la fase sólida\((x=0)\) permanece constante\(c_2\) y la concentración del componente (2) en el sólido antes de la difusión es uniforme\(c_{2^{\prime}}\) (a). Bajo estas condiciones límite, la solución a la segunda ley de Fick asume la forma:

\(\dfrac{c_2-c}{c_2-c_{2^{\prime}}}=\operatorname{erf}\left(\dfrac{x}{2 \sqrt{D t}}\right)\)

Si ningún componente (2) está originalmente en la matriz sólida (1) (b), la solución anterior es más simple:

\ begin {alineado}
\ dfrac {c_2-c} {c_2} &=\ nombreoperador {erf}\ izquierda (\ dfrac {x} {2\ sqrt {D t}}\ derecha)\\
1-\ dfrac {c} {c_2} &=\ nombreoperador {erf}\ izquierda (\ dfrac {x} {2\ sqrt {t}}\ derecha)\
\ dfrac {c} {c_2} &=1-\ nombreoperador {erf}\ izquierda (\ dfrac {x} {2\ sqrt {D t}}\ derecha)\\
\ dfrac {c} {c_2} &=\ nombreoperador {erfc}\ izquierda (\ dfrac {x} {2\ sqrt {D t}}\ derecha)\\
c &=c_2\ texto {erfc}\ izquierda (\ dfrac {x} {2\ sqrt {D t}}\ derecha)
\ final {alineado}

Un análisis muestra que la última forma de la solución a la ley de Fick relaciona la concentración (c) en cualquier posición (\(\mathrm{x}\)) (profundidad de penetración en la matriz sólida) y el tiempo (t) con la concentración superficial\(\left(c_2\right)\) y la constante de difusión\((D)\). Los términos erf y erfc representan función de error y función de error complementaria respectivamente; es la función de error gaussiano como tabulada (como funciones trigonométricas y exponenciales) en tablas matemáticas. Sus valores limitantes son:

\ begin {aligned}
&\ text {erf} (0) &&= 0\\
&\ text {erf} (\ infty) &&= 1\ quad &&\ text {Y para la función de error complementaria:}\\
&\ text {erf} (-\ infty) &&=-1\ quad &&\ text {erfc = (1-erf)}
\ end {alineado}

Otra mirada a la solución anterior a la ecuación de difusión muestra que la concentración (c) del componente (2) en el sólido se expresa en términos de la función de error del argumento\(x / 2 \sqrt{D t}\). Para determinar a qué profundidad aparecerá una concentración particular\(\left(\mathrm{c}^*\right)\) de (2), sustituimos esta concentración por (c) y obtenemos:

\(\dfrac{c^*}{c_2}=\operatorname{erfc}\left(\dfrac{x}{2 \sqrt{D t}}\right)=K\)

Dado que la función error es una constante, su argumento también debe ser una constante:

Figura 7 Avance del frente de concentración (c*) en función del trime

\(\dfrac{x}{2 \sqrt{D t}}=K^{\prime}\)

Por lo tanto, bajo las condiciones de límite dadas:

\ begin {alineado}
&x=k^ {\ prime} 2\ sqrt {D t}\\
&x=k^ {\ prime}\ cdot\ sqrt {D t}\\
&x\ propto\ sqrt {t}
\ end {alineado}

Se encuentra que la profundidad de penetración de una concentración especificada es proporcional a la raíz cuadrada del tiempo de difusión.

4. AUTO-DIFUSIÓN

Como se indicó anteriormente, el movimiento térmico de los átomos en una red es un proceso aleatorio y como tal conducirá a desplazamientos locales de átomos individuales. Este movimiento aleatorio de átomos dentro de una red (autodifusión), que no está asociado con ningún gradiente de concentración existente, se puede demostrar fácilmente con la ayuda de “elementos radiactivos”. Por ejemplo, el níquel aparece en la naturaleza en forma de varios “isótopos estables”:

\(\mathrm{Ni}_{28}^{58}, \mathrm{Ni}_{28}^{60}, \mathrm{Ni}_{28}^{61}, \mathrm{Ni}_{28}^{62}\)y\(\mathrm{Ni}_{28}^{64}\)

Si\(\mathrm{Ni}_{28}^{58}\) se irradia con neutrones en un reactor nuclear, capturará un neutrón y se convertirá en el\(\mathrm{Ni}_{28}^{59}\) que es radiactivo (un radioisótopo).

\(\mathrm{Ni}_{28}^{58}+\mathrm{n} \rightarrow \mathrm{Ni}_{28}^{59} \rightarrow \mathrm{Co}_{27}^{59}+\gamma+\beta\)

El níquel 59 se caracteriza por su inestabilidad que conduce a la emisión de\(\beta\) y\(\gamma\) radiación, con una vida media de\(8 \times 10^4\) años. Dado que esta radiación puede medirse mediante detectores de radiación apropiados, es posible utilizarla\(\mathrm{Ni}_{59}\) como “elemento trazador” para estudios de autodifusión.

El níquel radiactivo (que es idéntico al níquel ordinario con la excepción de sus propiedades radiactivas) es electrochapado sobre níquel normal. Este espécimen se coloca posteriormente en un horno y se calienta hasta cerca de su punto de fusión durante un período prolongado de tiempo. Después de retirar el espécimen, se secciona en rodajas paralelas a la superficie que contenía el elemento trazador radiactivo. Con la ayuda de un detector de radiación ahora se puede demostrar que el\(\mathrm{Ni}_{59}\), que originalmente estaba solo en la superficie, se ha difundido en el material a granel mientras que simultáneamente algo de níquel a granel se ha contradifundido en la otra dirección. Si esta muestra es tratada térmicamente durante mucho más tiempo, el seccionamiento y conteo revelará una distribución completamente uniforme del elemento radiotrazador. Así, se puede demostrar que la auto-difusión ocurre en los sólidos, y las mediciones cuantitativas con elementos trazadores incluso permiten la determinación de coeficientes de autodifusión.

5. MECANISMOS DE DIFUSIÓN

El proceso de difusión en soluciones sólidas intersticiales, como el del carbono en el hierro, puede entenderse fácilmente como resultado de diferencias considerables en los diámetros atómicos. Sin embargo, el hecho de que se\(\mathrm{Au}\) difunde más rápido\(\mathrm{Pb}\) que se\(\mathrm{NaCl}\) difunde en el agua\(15^{\circ} \mathrm{C}\) no se puede explicar fácilmente. La magnitud de la energía de activación observada indica que hay que excluir un mecanismo por el cual los átomos simplemente cambian de lugar entre sí. Frenkel y Schottky sugirieron mecanismos más razonables. Propusieron la existencia de defectos puntuales (vacantes) en cristales que proporcionan un mecanismo por el cual los átomos pueden moverse (difundirse) dentro de un cristal. La concentración de tales vacantes, como usted recuerda, se puede calcular a partir de simples cálculos estadísticos.

En la mayoría de los sólidos no se trata de monocristales sino de materiales policristalinos que contienen un gran número de límites de grano (superficies internas). Como era de esperar, la tasa de difusión a lo largo de los límites de grano es mucho mayor que la de la difusión volumétrica (\(D_{\text {volume }}<D_{\text {g-boundary }}\)). Finalmente, la difusión superficial, que tiene lugar en todas las superficies externas, es aún mayor\(\left(D_{\text {volume }}<D_{\text {g-boundary }}<D_{\text {surface }}\right)\). Las respectivas energías de activación para difusión son:

\(E_a\)\(<E_a\)volumen\(<E_a\) de límite de grano superficial

Difusión en no metales

En los sistemas no metálicos la difusión se realiza por los mismos mecanismos que en los sistemas metálicos. El oxígeno, por ejemplo, se difunde a través de muchos óxidos por migración de vacantes. En los óxidos cristalinos y también en los vidrios de silicato, se encuentra que el oxígeno se difunde mucho más rápidamente que el ion metálico. En los vidrios que contienen átomos alcalinos\(\left(\mathrm{Na}^{+}, \mathrm{K}^{+}\right)\), las respectivas velocidades de difusión son:

\[D_{\text {alkali }}>D_{\text {oxygen }}>D_{\text {silicon }}\]

correspondientes a diferencias en las resistencias de unión. En materiales poliméricos, la difusión requiere el movimiento de moléculas grandes ya que la unión intramolecular es mucho más fuerte que la unión intermolecular. Este hecho explica que las tasas de difusión en dichos materiales son relativamente pequeñas.

Difusión gaseosa en sólidos

Algunos gases, como el hidrógeno y el helio, se difunden a través de algunos metales con facilidad incluso a temperatura ambiente. El helio, por ejemplo, se difundirá a través del cuarzo y el acero y limita el vacío definitivo que se puede obtener en sistemas de ultra alto vacío. De manera similar, el hidrógeno se difunde fácilmente\(\mathrm{Ni}\) a temperaturas elevadas. \(\mathrm{H}_2\)también se difunde a altas velocidades a través del paladio, fenómeno que se usa ampliamente para la purificación del hidrógeno ya que ese material es impermeable a otros gases.

TABLA 2: La función de error

\(z\)	\(erf(z)\)	\(z\)	\(erf(z)\)
\ (z\) ">0	\ (erf (z)\) ">0	\ (z\) ">0.85	\ (erf (z)\) ">0.7707
\ (z\) ">0.025	\ (erf (z)\) ">0.0282	\ (z\) ">0.90	\ (erf (z)\) ">0.7970
\ (z\) ">0.05	\ (erf (z)\) ">0.0564	\ (z\) ">0.95	\ (erf (z)\) ">0.8209
\ (z\) ">0.10	\ (erf (z)\) ">0.1125	\ (z\) ">1.0	\ (erf (z)\) ">0.8427
\ (z\) ">0.15	\ (erf (z)\) ">0.1680	\ (z\) ">1.1	\ (erf (z)\) ">0.8802
\ (z\) ">0.20	\ (erf (z)\) ">0.2227	\ (z\) ">1.2	\ (erf (z)\) ">0.9103
\ (z\) ">0.25	\ (erf (z)\) ">0.2763	\ (z\) ">1.3	\ (erf (z)\) ">0.9340
\ (z\) ">0.30	\ (erf (z)\) ">0.3286	\ (z\) ">1.4	\ (erf (z)\) ">0.9523
\ (z\) ">0.35	\ (erf (z)\) ">0.3794	\ (z\) ">1.5	\ (erf (z)\) ">0.9661
\ (z\) ">0.40	\ (erf (z)\) ">0.4234	\ (z\) ">1.6	\ (erf (z)\) ">0.9763
\ (z\) ">0.45	\ (erf (z)\) ">0.4755	\ (z\) ">1.7	\ (erf (z)\) ">0.9838
\ (z\) ">0.50	\ (erf (z)\) ">0.5205	\ (z\) ">1.8	\ (erf (z)\) ">0.9891
\ (z\) ">0.55	\ (erf (z)\) ">0.5633	\ (z\) ">1.9	\ (erf (z)\) ">0.9928
\ (z\) ">0.60	\ (erf (z)\) ">0.6039	\ (z\) ">2.0	\ (erf (z)\) ">0.9953
\ (z\) ">0.65	\ (erf (z)\) ">0.6420	\ (z\) ">2.2	\ (erf (z)\) ">0.9981
\ (z\) ">0.70	\ (erf (z)\) ">0.6778	\ (z\) ">2.4	\ (erf (z)\) ">0.9993
\ (z\) ">0.75	\ (erf (z)\) ">0.7112	\ (z\) ">2.6	\ (erf (z)\) ">0.9998
\ (z\) ">0.80	\ (erf (z)\) ">0.7421	\ (z\) ">2.8	\ (erf (z)\) ">0.9999

 

FUENTE: Los valores de erf (z) a 15 lugares, en incrementos de z de 0.0001, se pueden encontrar en el Proyecto de Tablas Matemáticas, “Tabla de Funciones de Probabilidad.”, vol. 1, Agencia Federal de Obras, Administración de Proyectos de Obras, Nueva York, 1941. Una discusión sobre la evaluación de erf (z), sus derivados e integrales, con una breve tabla la dan H. Carslaw y J. Jaeger, en el Apéndice 2 de “Conducción de Calor en Sólidos”, Oxford University Press, Fair Lawn, NJ, 1959.