9.1: Radios iónicos y relaciones de radio
- Page ID
- 72237
Los átomos en los cristales se mantienen unidos por fuerzas electrostáticas, interacciones de van der Waals y enlaces covalentes. De ello se deduce que las disposiciones de los átomos que pueden maximizar la fuerza de estas interacciones atractivas deberían ser las más favorables y conducir a las estructuras cristalinas más comúnmente observadas.
Reglas de relación de radio
Los primeros cristalógrafos tuvieron problemas para resolver las estructuras de sólidos inorgánicos mediante difracción de rayos X debido a que algunas de las herramientas matemáticas para analizar los datos aún no se habían desarrollado. Una vez que se propuso una estructura de prueba, era relativamente fácil calcular el patrón de difracción, pero era difícil ir por el otro lado (del patrón de difracción a la estructura) si no se sabía nada a priori sobre la disposición de los átomos en la celda unitaria. Fue (¡y todavía lo es!) importante desarrollar algunas pautas para adivinar los números de coordinación y geometrías de unión de átomos en cristales. Las primeras reglas de este tipo fueron propuestas por Linus Pauling, quien consideró cómo se podrían empacar esferas cargadas opuestamente de diferentes radios. Pauling propuso a partir de consideraciones geométricas que la calidad del “ajuste” dependía de la relación de radio del anión y el catión.
|
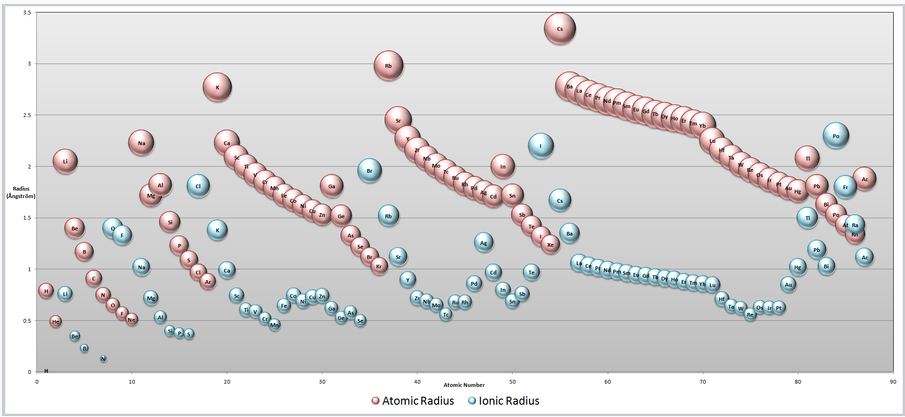
Radios Atómicos e Iónicos. Tenga en cuenta que los cationes son siempre más pequeños que el átomo neutro (rosa) del mismo elemento, mientras que los aniones son más grandes. Al pasar de izquierda a derecha a través de cualquier fila de la tabla periódica, los átomos neutros y cationes se contraen en tamaño debido al aumento de la carga nuclear. (haga clic para ampliar la imagen) |
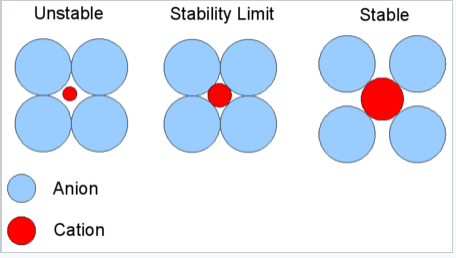
La idea básica de las reglas de relación de radio se ilustra a la derecha. Consideramos que el anión es el átomo de empaquetamiento en el cristal y el catión más pequeño llena los sitios intersticiales (“agujeros”). Los cationes encontrarán arreglos en los que puedan contactar con el mayor número de aniones. Si el catión puede tocar todos sus aniones vecinos más cercanos, como se muestra a la derecha para un catión pequeño en contacto con aniones más grandes, entonces el ajuste es bueno. Si el catión es demasiado pequeño para un sitio dado, ese número de coordinación será inestable y preferirá una estructura de coordinación más baja. La siguiente tabla da los rangos de relaciones catión/radio anión que dan el mejor ajuste para una geometría de coordinación dada.
|
Relación de Radio Crítico. Este diagrama es para la coordinación número seis: se muestran 4 aniones en el plano, 1 está por encima del plano y 1 por debajo. El límite de estabilidad está a r C/r A = 0.414 |
| Número de coordinación | Geometría | ρ = r catión /r anión |
|---|---|---|
| 2 | lineal | 0 - 0.155 |
| 3 | triangular | 0.155 - 0.225 |
| 4 | tetraédrico | 0.225 - 0.414 |
| 4 | plano cuadrado | 0.414 - 0.732 |
| 6 | octaédrico | 0.414 - 0.732 |
| 8 | cúbico | 0.732 - 1.0 |
| 12 | cuboctaédrico | 1.0 |
Desafortunadamente, hay varios desafíos con el uso de esta idea para predecir estructuras cristalinas:
- No conocemos los radios de los iones individuales
- Los átomos en los cristales no son realmente iones - hay un grado variable de covalencia dependiendo de las diferencias de electronegatividad
- Las distancias de enlace (y por lo tanto los radios iónicos) dependen de la fuerza de unión y el número de coordinación (recuerde la regla de Pauling D (n) = D (1) - 0.6 log n)
- Los radios iónicos dependen del estado de oxidación (carga más alta => tamaño de catión más pequeño, tamaño de anión más grande)
Podemos construir una tabla de radios iónicos asumiendo que la longitud del enlace es la suma de los radios (r + + r -) si los iones están en contacto en el cristal. Consideremos por ejemplo los compuestos MgX y MnX, donde X = O, S, Se. Todos estos compuestos cristalizan en la estructura de NaCl:
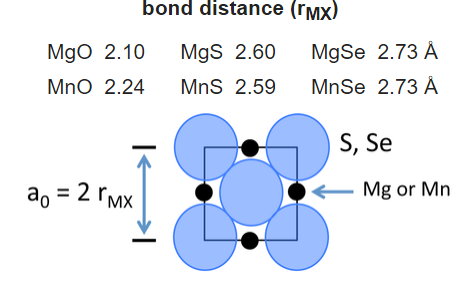
Para los dos aniones más grandes (S 2- y Se 2-), las dimensiones de la celda unitaria son las mismas para ambos cationes. Esto sugiere que los aniones están en contacto en estas estructuras. A partir de consideraciones geométricas, el radio del anión en este caso viene dado por:
\[r_{_}= \frac{r_{MX}}{\sqrt{2}}\]
y así los radios de los iones S2- y Se 2- son 1.84 y 1.93 Å, respectivamente. Una vez fijados los tamaños de estos aniones, podemos obtener un conjunto autoconsistente de radios catiónicos y aniónicos a partir de las constantes reticulares de muchos compuestos MX.
¿Qué tan bien funciona este modelo? Consideremos las estructuras de los óxidos metálicos tetravalentes (MO 2), usando radios Pauling y las predicciones del modelo de relación de radio:
| Óxido MO 2 | Relación de radio | Coord previsto. no. | Coord observado no. (estructura) |
|---|---|---|---|
| CO 2 | ~0.1 | 2 | 2 (molécula lineal) |
| SiO 2 | 0.32 | 4 | 4 (varias estructuras tetraédricas) |
| GeO 2 | 0.43 | 4 | 4 (estructuras similares a la sílica) |
| “ | 0.54 | 6 | 6 (rutilo) |
| TiO 2 | 0.59 | 6 | 6 (rutilo) |
| ZrO 2 | 0.68 | 6 | 7 (baddleyita) |
| “ | 0.77 | 8 | 8 (fluorita) |
| THO 2 | 0.95 | 8 | 8 (fluorita) |
Obsérvese que los cationes tienen radios diferentes dependiendo de sus números de coordinación, y así se calculan diferentes relaciones de radio para Ge 4+ con los números de coordinación 4 y 6, y para Zr 4+ con los números de coordinación 6 y 8.
Para esta serie de óxidos, el modelo parece funcionar bastante bien. El número de coordinación correcto se predice en todos los casos, y los casos límite como GeO 2 y ZrO 2 se encuentran en estructuras con diferentes números de coordinación. El modelo también predice correctamente las estructuras de BeF 2 (tipo SiO 2), MgF 2 (rutilo) y CaF 2 (fluorita).
¿Qué pasa con los haluros alcalinos NaCl, KBr, LiI, CsF, etc.? Todos ellos tienen la estructura de NaCl excepto CsCl, CsBr y CsI, que tienen la estructura CsCl (8-8). En este caso el modelo de relación de radio falla bastante mal. Se predice que las sales LiBr y LiI de Li + tienen estructuras tetraédricas, y se predice que KF tiene una estructura 8-8 como CsCl. Podemos intentar ajustar los radios (por ejemplo, hacer los cationes más grandes y los aniones más pequeños), pero lo mejor que podemos hacer con los haluros alcalinos es predecir aproximadamente la mitad de sus estructuras correctamente. Dado que los haluros alcalinos son compuestos claramente iónicos, esta falla sugiere que hay algo muy mal con el modelo de relación de radio, y su éxito con compuestos MO 2 fue coincidente.
Además de la regla de la relación de radio, Linus Pauling desarrolló otras reglas útiles que son útiles para racionalizar y predecir las estructuras de compuestos inorgánicos. Las reglas de Pauling [1] establecen que:
- Las estructuras estables son localmente electroneutrales. Por ejemplo, en la estructura de la perovskita doble Sr 2 FeMoO 6, MO 6 (M = Fe 2+, Mo 6+) octaedros comparten todos sus vértices, y los iones Sr 2+ llenan las cavidades cubooctaédricas que están flanqueadas por ocho octaedros MO 6. [2] Cada ion O 2- se coordina a un ion Fe 2+ y un ion Mo 6+ para lograr la electroneutralidad local, y así los octaedros FeO 6 y MoO 6 se alternan en la estructura.
- Se debe minimizar la repulsión catión-catiónica. Los poliedros aniónicos pueden compartir vértices (como en la estructura de la perovskita) sin ninguna penalización energética. Los bordes poliédricos compartidos, y especialmente los rostros compartidos, causan repulsión catión-catiónica y deben evitarse. Por ejemplo, en el rutilo, el polimorfo más estable de TiO 2, los octaedros de TiO 6 comparten vértices y dos bordes opuestos, formando cintas en la estructura. En anatasa TiO 2, cada octaedro comparte cuatro bordes por lo que el polimorfo anatasa es menos estable termodinámicamente.
- Los cationes altamente cargados en los poliedros aniónicos tienden a no compartir bordes o incluso vértices, especialmente cuando el número de coordinación es bajo. Por ejemplo, en ortosilicatos como el olivino (M 2 SiO 4), hay SiO 4 - tetraedros aislados.
|
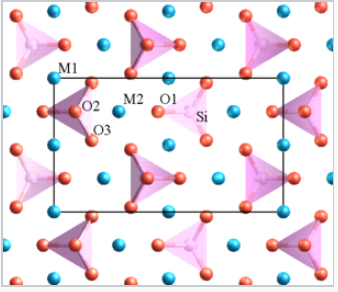
Estructura del olivino. M (Mg o Fe) = esferas azules, Si = tetraedros rosados, O = esferas rojas. |
Como veremos pronto, todas las reglas de Pauling se justifican sobre la base de consideraciones de energía de celosía. En los compuestos iónicos, la disposición de los átomos que maximiza las interacciones anión-catión mientras minimiza los contactos catión-catión y anión-anión es energéticamente la mejor.