9.14: Problemas
- Page ID
- 72137
1. Use energías de celosía para explicar por qué MgSO 4 se descompone en óxido de magnesio y SO 3 a una temperatura mucho más baja que la de BasO 4.
2. El MgO sólido podría formularse como Mg + O - o Mg 2 + O 2-. Utilice los datos termoquímicos a continuación (algunos de los cuales son irrelevantes) y la fórmula de Kapustinskii para determinar cuál es más estable. La constante reticular para MgO (estructura de NaCl) es de 4.213 Å. Si bien la idea de un O - ion puede parecer extraña, tenga en cuenta que la segunda afinidad electrónica de O y el segundo potencial de ionización de Mg (en la tabla siguiente) son ambas bastante endotérmicas.
| Reacción | ∆H o, kJ/mol |
|---|---|
| Mg (s) = Mg (g) | 148 |
| Mg (g) = Mg + (g) + e - | 739 |
| Mg + (g) = Mg 2 + (g) + e - | 1,452 |
| O 2 (g) = 2 O (g) | 498 |
| O (g) + e - = O - (g) | -141 |
| O - (g) + e - = O 2- (g) | 790 |
3. A partir del calor de formación del sólido NH 4 Cl (-315 kJ/mol) y el NH 3 gaseoso (-46), las energías de disociación de enlaces de H 2 (436) y Cl 2 (244), el potencial de ionización del hidrógeno atómico (1,311) y la afinidad electrónica del cloro atómico (-349), calculan el afinidad protónica en fase gaseosa de NH 3. La energía reticular de NH 4 Cl puede estimarse a partir de la fórmula de Kapustinskii usando r N-Cl = 3.50 Å.
4. Las botellas de amoníaco acuoso a menudo se etiquetan como “hidróxido de amonio”. Vamos a probar esta idea utilizando un cálculo de energía de celosía para determinar si la sal NH 4 + OH - puede existir.
Los calores de formación de OH- y H 2 O gaseosos son respectivamente -141 y -242 kJ/mol. Suponiendo que NH 4 + es aproximadamente del mismo tamaño que Rb +, y OH -aproximadamente el mismo tamaño que F -, usando la fórmula de Kapustinskii, radios iónicos y la afinidad de protones NH 3 calculada en el problema 3, determinar si NH 4 + OH - debe ser una sal estable con respecto a NH 3 y H 2 O. A qué temperatura debe NH 4 + Cl - ser inestable con respecto a NH 3 y HCl, si ΔH f o para HCl es -92 kJ/mol y ΔS o (\(\ce{NH4Cl -> NH3 + HCl}\)) = 280 J/mol K?
5. El metal litio se quema en nitrógeno para hacer el nitruro Li 3 N. Los metales alcalinos más pesados (K, Rb, Cs) pueden formar azidas estables (MN 3), pero no nitruros M 3 N. Explique por qué esto es así.
6. (a) ¿Espera que BasO 4 o MgSO 4 sean más solubles en agua? b) ¿El LiF es más soluble que el LiClO 4? Explique.
7. ¿Qué polimorfo de ZnS (zincblende o wurzita) esperaría que fuera más estable sobre la base de la energía electrostática?
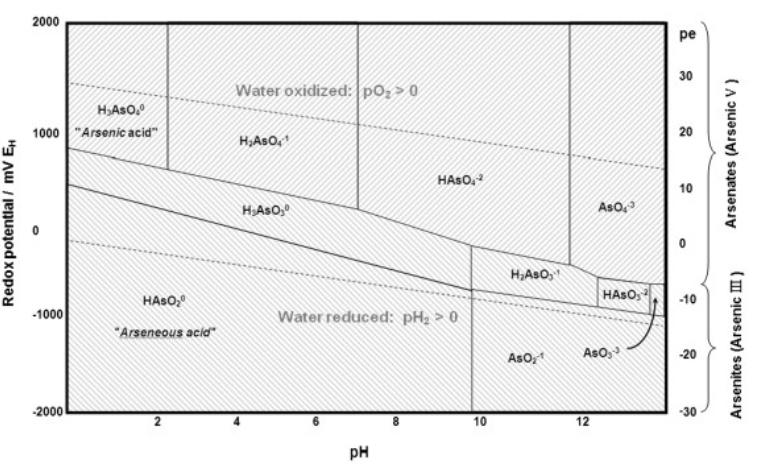
8. La contaminación por arsénico de las aguas subterráneas es un problema grave en Bangladesh, Chile, Argentina y otras partes del mundo, incluido el oeste de Estados Unidos. La intoxicación por arsénico se ha generalizado en el delta del río Ganges, donde los pozos tubulares traen agua contaminada desde 20-100 metros por debajo de la superficie. Un tratamiento sencillo que se ha propuesto es precipitar el arsénico por aireación del agua de pozo, que también contiene altas concentraciones de Fe 2 +. Haciendo referencia al diagrama Pourbaix de arsénico a continuación y al diagrama Pourbaix de hierro en el Capítulo 4, identificar las especies de hierro y arsénico que están presentes en el agua aireada a pH neutro. ¿Qué compuesto insoluble precipita para disminuir la concentración de arsénico? (Pista: ¿qué compuesto tendría la mayor energía de celosía?)