Saltar al contenido principal
LibreTexts Español

10.10: Problemas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    71891

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

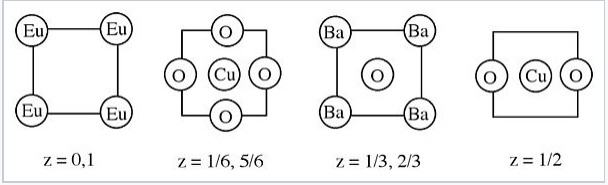
    1. A continuación se muestra la estructura de un superconductor de alta temperatura que contiene bario, europio, cobre y oxígeno. ¿Cuáles son los entornos de coordinación del Cu en este recinto? Esta estructura en realidad está estrechamente relacionada con la perovskita, ABO 3. Explicar la relación entre esta estructura y la estructura ideal de perovskita.

    A la izquierda hay una celda unitaria de europio con valores z de cero y uno. A continuación se presenta una celda unitaria de cobre y oxígeno con valores z de un sexto y cinco sextos. A continuación se presenta la celda unitaria de bario con valores z de un tercio y dos tercios. El último a la derecha es una celda unitaria de cobre y oxígeno con un valor z de la mitad.

    2. VO 2 puede existir en forma aislante o metálica, dependiendo de la temperatura y la presión. ¿Qué forma se estabilizaría aumentando la temperatura? Explica tu respuesta.

    3. Explique brevemente cómo y por qué los intervalos de banda para los semiconductores del bloque p del octeto varían (1) con el número cuántico principal promedio, y (2) con la diferencia de electronegatividad entre anión y catión.

    4. Indicar el tipo de conducción (n o p) en lo siguiente: (a) GaAs dopados con SE, (b) INAs 1 -x, donde x << 1, (c) Li 0.05 Ni 0.95 O, (d) Li x WO 3, donde x << 1.

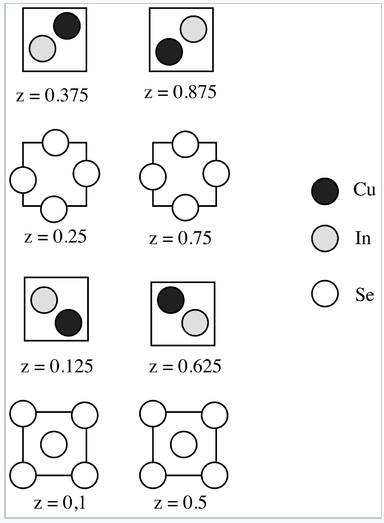
    5. La estructura del seleniuro de cobre indio, un semiconductor utilizado en células solares de película delgada, se muestra a continuación en secciones.

    a) ¿Cuál es la estequiometría del compuesto?

    b) ¿Qué tipo de dopaje (n o p) ocurrirá si se sustituye por selenio una pequeña cantidad de yodo?

    c) ¿Qué tipo de dopaje (n o p) ocurrirá si una pequeña fracción de los sitios de indio están ocupados por átomos de cobre?

    El punto negro es C u, el punto gris es In y el punto blanco es Se. En la parte superior izquierda hay una celda unitaria con un punto gris y un punto negro con un valor z de 0.375. Debajo hay una celda unitaria con cuatro puntos blancos y un valor z de 0.25. Debajo hay una celda unitaria con un punto gris y un punto negro con un valor z de 0.125. Last es una celda unitaria con cinco puntos blancos y valores z de cero y uno. La celda unitaria en la parte superior derecha tiene un punto gris y un punto negro con un valor z de 0.875. Debajo hay una celda unitaria con cuatro puntos blancos y un valor z de 0.75. Debajo hay una celda unitaria con un punto gris y un punto negro con un valor z de 0.625. Por último, hay una celda unitaria con cinco puntos blancos y un valor z de 0.5

    6. Usando 1 eV = 1240 nm, predecir los colores de anatasa TiO 2 (Eg = 3.1 eV), SiC (2.0 eV), ZnSnP 2 (1.7 eV), ZnGeP 2 (1.9 eV) e InP (1.27 eV).

    7. La conductividad de cierto semiconductor intrínseco (no dopado) aumenta en un factor de dos cuando la temperatura se eleva de 300 a 330 K. ¿Cuál es la banda prohibida (en eV)? R = 8.314 J/mol-K, 1 EV/átomo = 96.52 kJ/mol.

    8. Pure Ge es mucho más conductor que el Si puro. Dados sus bandgaps (0.74 y 1.15 eV, respectivamente), estiman la relación de sus conductividades a temperatura ambiente.

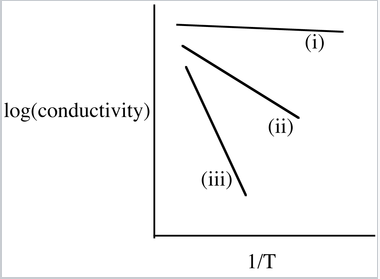
    9. La siguiente figura ilustra las tendencias en conductividad vs. temperatura inversa para Si, Ge y Ge dopado con As. Identificar las líneas (i), (ii) y (iii) con los materiales apropiados. Explique por qué la pendiente de la línea (i) es cercana a cero.

    clipboard_e0aedf7ec041f36ed46404530a9ead746.png

    10. Esbozar una unión p-n de silicio, mostrando la región de agotamiento, la flexión de la banda y el nivel de Fermi en ausencia de luz o potencial aplicado. En la oscuridad, la unión p-n actúa como rectificador. (a) ¿De qué manera los electrones y los agujeros fluyen más fácilmente en la oscuridad? b) ¿El campo eléctrico construido aumenta o disminuye bajo polarización directa? (c) A la luz, la unión actúa como fotodiodo. En este caso, bajo condiciones de cortocircuito, ¿fluyen los electrones en la misma dirección o en sentido contrario que en (a)? Explicar.

    This page titled 10.10: Problemas is shared under a CC BY-SA 4.0 license and was authored, remixed, and/or curated by Chemistry 310 (Wikibook) via source content that was edited to the style and standards of the LibreTexts platform.