Problemas con la tarea Capítulo 1
- Page ID
- 70090
Problemas con la tarea
Sección 1
Ejercicio 1
El cobalto forma dos sulfuros, CoS y Co 2 S 3. Predecir la relación de las masas de azufre que se combinan con una masa fija de cobalto para formar CoS y Co 2 S 3
- Contestar
-
En Co 2 S 3 hay 1.5 átomos de S por átomo de Co
En CoS hay 1 átomo de S por átomo de Co
La relación en masa de S en los dos compuestos es 1:1 .5 = 2:3
Ejercicio 2
¿Qué es cierto sobre el modelo de átomo de Rutherford?
a) Explica por qué los átomos no envían radiación electromagnética de forma permanente
b) Explica por qué las partículas alfa se dispersan por los átomos
c) Explica el espectro atómico del átomo de hidrógeno
d) Explica el dualismo onda-partícula
- Contestar
-
b) Explica por qué las partículas alfa se dispersan por los átomos
Ejercicio 3
El radio de Bohr (el radio de la órbita electrónica para el átomo H en su estado base) es de 5.29 x 10 -11 m. Calcular el radio de un electrón en la tercera capa del átomo H de acuerdo con el modelo de átomo de Bohr.
- Contestar
-
r 3 = 3 2 x 5.29 x 10 -11 m = 47.61 x 10 -11 m.
Sección 2
Ejercicio 1
El electrón en un átomo de H experimenta una transición electrónica de la tercera a la segunda capa. ¿Qué frecuencia tiene la luz que se emite? La energía del electrón en la primera capa es -2.18 x 10 -18 J.
- Contestar
-
Energía del electrón en la tercera capa: E 3 = -2.18 x 10 -18 J/3 2 = -0.24 x 10 -18 J
Energía del electrón en la 2ª cáscara: E 2 = -2.18 x 10 -18 J/2 2 = -0.545 x 10 -18 J
Diferencia de energía entre los dos electrones: E 3 -E 2 = 0.305 x 10 -18 J
Frecuencia de la luz emitida: n= (E 3 -E 2) /h = 0.305 x 10 -18 J/ 6.63 x 10 -34 Js = 4.60 x 10 14 s -
Ejercicio 2
¿Cuál es la masa de un fotón con una longitud de onda de 400 nm que viaja a través del espacio?
- Contestar
-
λ = h/mc —> m = h/λc = 6.63 x 10 -34 Js/(400 x 10 -9 m x 3.00 x 10 8 m/s) = 5.525 x 10 -36 kg.
Ejercicio 3
Dos objetos se mueven a la misma velocidad. ¿Cuáles (en su caso) de las siguientes afirmaciones son ciertas?
a) La longitud de onda DeBroglie del objeto más pesado es más larga que la del más ligero.
b) Si un objeto tiene el doble de masa que el otro, su longitud de onda es la mitad del otro
c) Duplicar la velocidad de uno de los objetos tendrá el mismo efecto en su longitud de onda que duplicar su masa.
- Contestar
-
a) Si un objeto tiene el doble de masa que el otro, su longitud de onda es la mitad del otro
b) Duplicar la velocidad de uno de los objetos tendrá el mismo efecto en su longitud de onda que duplicar su masa
Ejercicio 4
La potencia de un láser rojo con una longitud de onda de 630 nm) es de 1.00 Watt (1.00 Js). ¿Cuántos fotones por segundo emite el láser?
- Contestar
-
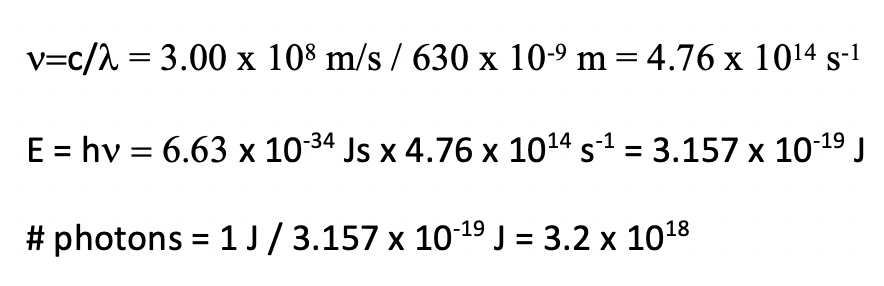
Ejercicio 5
¿Cuál de las siguientes olas considerarías que es onda de materia estacionaria?
a) La vibración de un tambor.
b) Sonido viajando al aire libre.
c) Un tsunami.
d) Ninguna de las anteriores.
- Contestar
-
a) La vibración de un tambor.
Ejercicio 6
Supongamos que un electrón viaja en una caja unidimensional (como se discute en clase) de la longitud de 1 m. Busque constantes relevantes en internet o un libro de texto adecuado.
a) ¿Cuál es la longitud de onda de la onda de materia estacionaria asociada en el estado fundamental?
b) ¿Cuál es la velocidad del electrón en el estado fundamental?
c) ¿Cuál es la energía del electrón en el estado fundamental?
- Contestar
-
a)
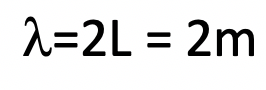
b)
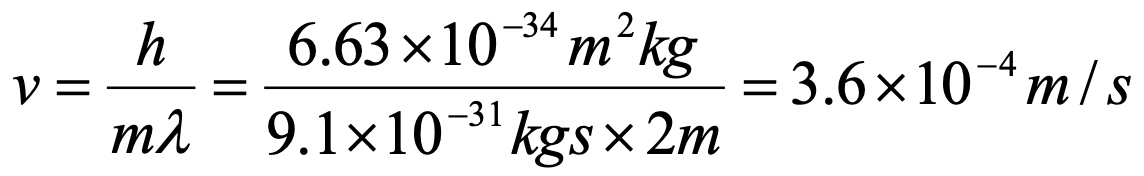
c)
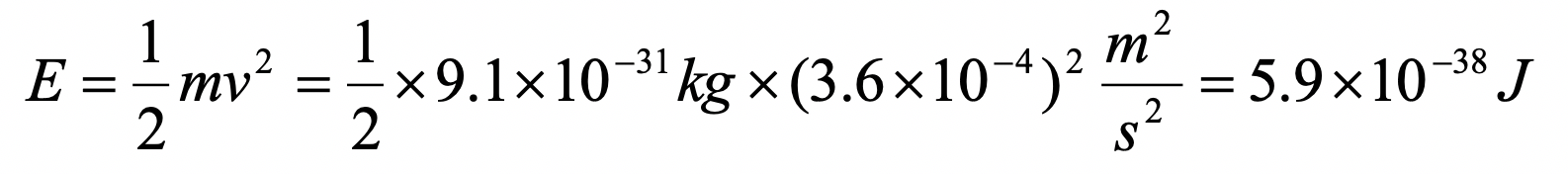
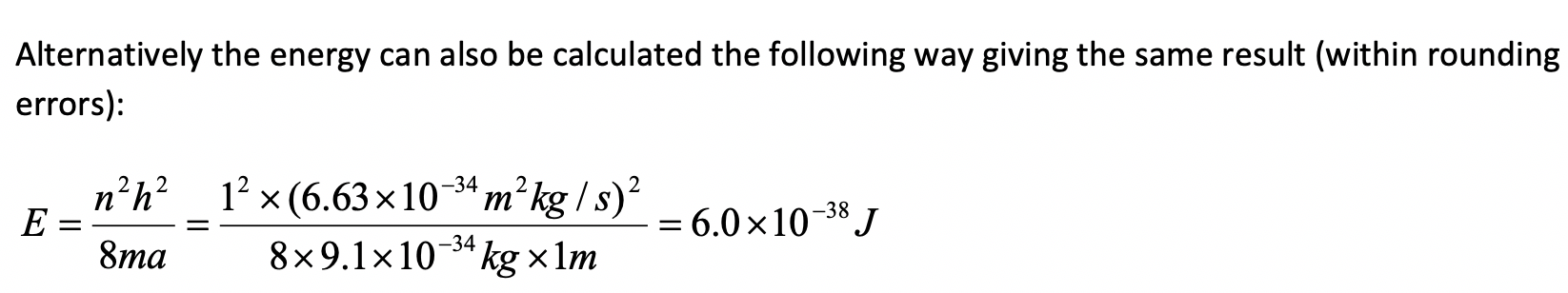
Ejercicio 7
Un electrón en el primer estado excitado viaja con una velocidad de 15 m/s dentro de una caja unidimensional. ¿Cuál es la longitud de la caja?
- Contestar
-
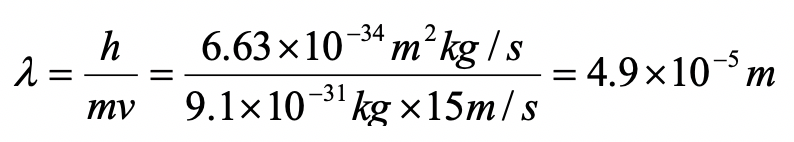
En el primer estado excitado n =2. Para n = la longitud de la caja es igual a la longitud de onda. Por lo tanto, la longitud de la caja es de 4.9 x 10 -5 m.
Ejercicio 8
¿Qué son los orbitales (más de una respuesta puede ser correcta)?
a) Funciones de onda que describen los electrones como ondas tridimensionales de materia estacionaria en un átomo.
b) Espacios dentro de un átomo en el que el electrón viaja como una partícula clásica.
c) Soluciones de la ecuación de Schroedinger para el átomo de hidrógeno.
- Contestar
-
a) Funciones de onda que describen los electrones como ondas tridimensionales de materia estacionaria en un átomo.
c) Soluciones de la ecuación de Schroedinger para el átomo de hidrógeno.
Ejercicio 9
¿Qué números cuánticos l están permitidos cuando el número cuántico n es 4?
- Contestar
-
l puede ser 3,2,1,0
Ejercicio 10
¿Qué números cuánticos m están permitidos cuando el número cuántico l es 3?
- Contestar
-
-3, -2, -1,0, +1, +2, +3
Ejercicio 11
¿Qué es cierto acerca de la siguiente función de onda?
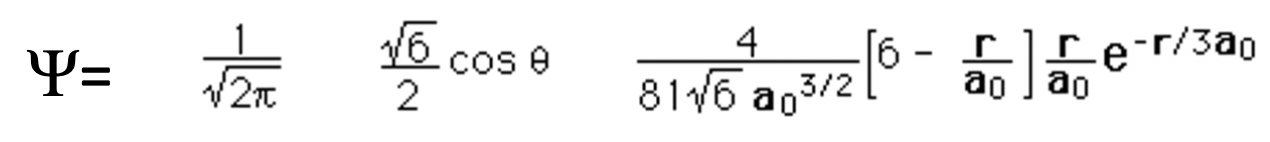
a) No tiene nodos angulares
b) No tiene nodos esféricos
c) Su amplitud es 0 en el núcleo
d) La función de onda representa una s orbital
- Contestar
-
c) Su amplitud es 0 en el núcleo
Ejercicio 12
La parte angular de la función de onda de un orbital tiene la siguiente forma:
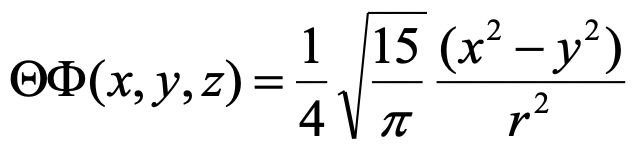
¿Qué planos son los nodos planos en esta órbita?
- Contestar
-
La función de onda es 0 para x=y y x=-y. Entonces son dos planos los que bisectan los ejes x e y.
Ejercicio 13
Ordene los siguientes orbitales con respecto a sus capacidades de penetración:
4s, 4p, 4d, 4f
- Contestar
-
4s > 4p > 4d > 4f
Ejercicio 14
¿Cuál es la carga nuclear efectiva sobre un electrón en un ion He +?
- Contestar
-
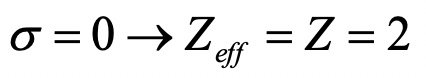
Ejercicio 15
Calcular la energía orbital de un electrón 3p en un átomo de azufre usando las reglas de Slater.
- Contestar
-
(1s 2) (2s 2 2p 6) (3s 2 3p 4)
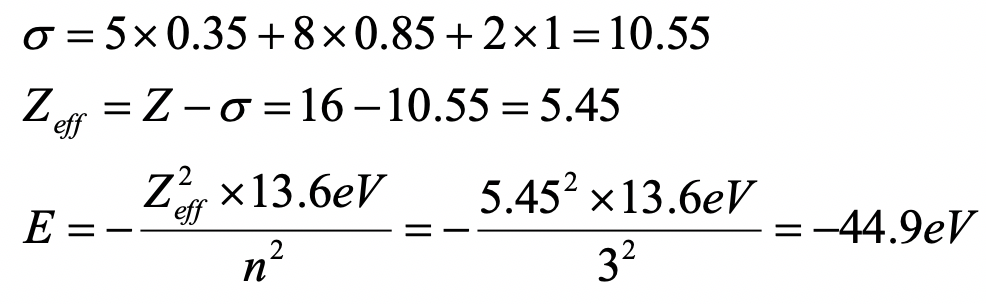
Ejercicio 16
Calcular la energía orbital de un electrón 3d en un átomo de paladio usando las reglas de Slater.
- Contestar
-
(1s 2) (2s 2 2p 6) (3s 2 3p 6) (3d 10) (4s 2 4p 6) (4d 8) (5s 2)
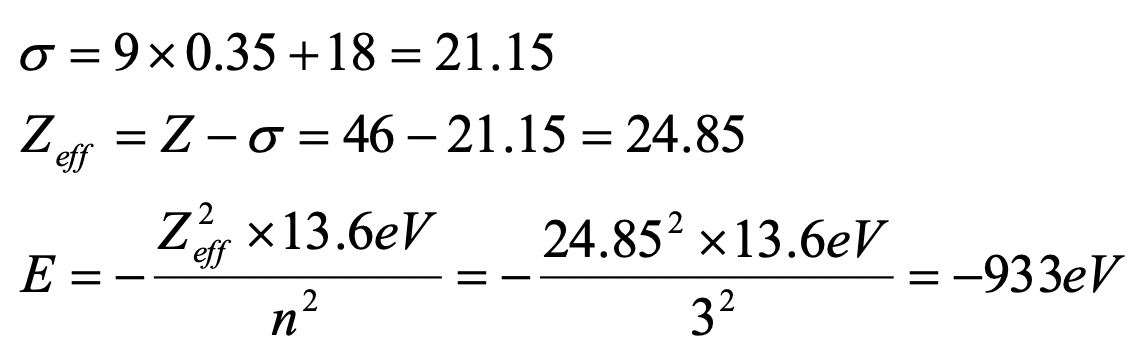
Ejercicio 17
Calcular cuánto mayor es la primera energía de ionización de un átomo de oxígeno en comparación con un átomo de flúor. Usa las reglas de Slater para responder a la pregunta.
- Contestar
-
O: (1s 2) (2s 2 2p 4)