2.1: Elementos de simetría y operaciones
- Page ID
- 70111
Simetría en Química
La simetría es en realidad un concepto de matemáticas y no de química. Sin embargo, la simetría y la teoría matemática subyacente para la simetría, la teoría de grupos, son de tremenda importancia en la química porque pueden aplicarse a muchos problemas químicos. Por ejemplo, nos ayuda a clasificar las estructuras de moléculas y cristales, comprender la unión química, predecir espectros vibracionales y determinar la actividad óptica de los compuestos. Por lo tanto, primero discutiremos los fundamentos generales de la simetría y la teoría de grupos, y luego los aplicaremos a problemas químicos, en particular la unión química.
Primero encontremos una definición para la simetría. La simetría nos resulta muy familiar ya que asociamos la simetría con la belleza, pero las cosas muy familiares no son necesariamente fáciles de definir científicamente. Una definición común es que la simetría es la auto-similitud de un objeto. Cuantas más partes similares tenga, más simétrica aparece. Por ejemplo, argumentaríamos que las dos alas de la mariposa representada se ven similares. Si el ala izquierda fuera muy diferente del ala derecha la mariposa se vería menos simétrica.
¿Cómo podemos medir cuantitativamente la auto-similitud o simetría de un objeto? Podemos hacer esto usando el concepto de la operación de simetría. Se define como un movimiento de un objeto en una orientación indistinguible equivalente. El número y tipo de operaciones de simetría que se pueden llevar a cabo definen la simetría del objeto.
Definición: Operación de simetría
Movimiento de un objeto en una orientación indistinguible equivalente
Las operaciones de simetría se realizan alrededor de los llamados elementos de simetría Un elemento de simetría es un punto, línea o plano sobre el cual se lleva a cabo una operación de simetría. Entender qué elementos de simetría y operaciones existen.
Definición: Elemento de simetría
Un punto, línea o plano sobre el cual se realiza una operación de simetría
La Operación Identidad (E)
La operación más sencilla es la operación de identidad. Se puede denotar con el símbolo de Schoenflies E. Los símbolos de Schoenflies son los símbolos más comunes para denotar una operación de simetría. La operación de identidad dice que cada objeto es autosimilar a sí mismo cuando no lo mueves de ninguna manera. Esta es una afirmación trivial, pero como veremos más adelante, la operación de identidad es necesaria para completar el marco matemático de la simetría, la teoría de grupos. La operación de identidad está presente en cualquier objeto. En el ejemplo de la concha de caracol representada es la única operación (Fig. 2.1.2).
La operación de rotación adecuada
La operación de rotación adecuada es una rotación en sentido antihorario alrededor de un eje de rotación apropiado en un ángulo de 360° sobre un número entero n. Después de esa rotación, el objeto debe ser indistinguible de su forma original. Eso significa que el objeto después de la rotación debe superponer el objeto original antes de la rotación. Por ejemplo, cuando n=4, entonces giramos alrededor de 90°, y después de eso el objeto debe superponer su forma original. El eje de rotación adecuado es el elemento de simetría asociado con la operación de rotación adecuada. Es el símbolo de Schoenflies es C n, por lo que n se llama el orden del eje de rotación. Una operación rotacional adecuada tiene el símbolo C n m, por lo que m cuenta el número de veces que se lleva a cabo la operación. En general giramos un ángulo de 360°× m/n cuando realizamos una operación C n m. Esto significa que cuando m=n, entonces hemos girado alrededor de 360° (Fig. 2.1.3). Entonces todos los puntos en el objeto están en su posición original. Es como si no hubiéramos hecho nada con el objeto. También podemos decir que hemos llegado a la identidad E. En forma matemática podemos decir que C n n =E. si giramos una vez más, C n (n+1), entonces esto sería igual a rotar solo una vez, y así C n (n+1) =C n 1. Por ejemplo, si n=4, entonces rotar cuatro veces alrededor de 90° producirá la identidad. Hemos girado alrededor de 4 x 90°=360° que es lo mismo aunque no habíamos girado en absoluto, porque todos los puntos del objeto están en su posición original después de una rotación de 360°. Si giramos 5 veces alrededor de 90°, sería lo mismo que rotar solo una vez.
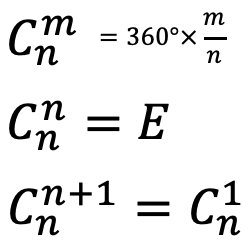
Si un objeto tiene varios ejes con diferente orden n, entonces el que tiene el orden más alto se denomina eje principal. Si hay más de un eje del mismo orden, entonces se distinguen por primos si no son conjugados. Aprenderemos sobre la definición exacta de conjugación algo más adelante, sin embargo a menudo podemos ver por inspección si dos ejes son conjugados. Este suele ser el caso cuando pasan a través del objeto de una manera equivalente, y giran el objeto de una manera equivalente. Ejes que pasan por menos muchos enlaces, obtienen menos muchos primos. Esto es sólo una convención, pero hay que seguirla. Una regla adicional es que un eje que está en la misma posición que el eje principal obtiene el menor número de primos. Por ejemplo, una molécula plana cuadrada como PtcL 4 2- tiene un eje principal C 4 que se encuentra perpendicular al plano cuadrado de la molécula. Hay un eje C 2 adicional donde discurre el eje C 4. Está presente porque también se puede girar alrededor de 180°, y no solo alrededor de 90°. Este eje C 2 no obtiene ningún primo. A ver que hay cuatro ejes C 2 adicionales, dos de ellos se denotan C 2 ', y otros dos se denotan C 2”. Se puede ver que los dos ejes que sólo tienen un primo pasan por dos enlaces Pt-Cl, mientras que los que tienen dos primos, no pasan por ningún enlace. Los dos ejes C 2 'son conjugados, lo que significa que transforman el objeto de una manera equivalente. Los dos ejes C 2” también son conjugados.
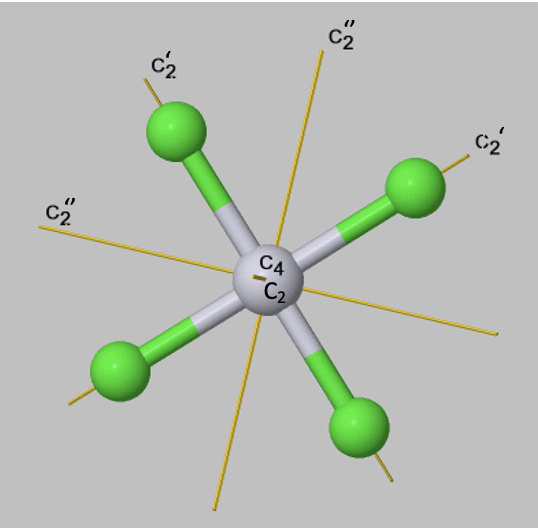
Ahora podemos pensar en cómo podemos escribir los ejes y sus operaciones rotacionales adecuadas asociadas de manera sistemática. Veamos primero los elementos de simetría, los ejes propios: Convencionalmente escribimos primero el eje principal, y luego todos los demás ejes desde su orden más alto hasta su orden más bajo. Cuando hay ejes del mismo orden, los que tienen el menor número de primos se denotan primero, y los que tienen el mayor número de primos duran. Si hay ejes conjugados entonces su número se coloca frente a su símbolo de Schoenflies. Para los ejes propios del PtcL 4 2- la notación sería por lo tanto: C 4, C 2, 2C 2 ', 2C 2”. Ahora veamos cómo denotar las operaciones de rotación que están asociadas con estos elementos de simetría. La notación sigue las mismas reglas que para los elementos de simetría. Además, hay que considerar que no debemos contar operaciones idénticas dos veces, tampoco denotamos las operaciones que son iguales a la identidad. Para el eje C 4 hay cuatro operaciones hasta llegar a la identidad. C 4 1, C 4 2, C 4 3 y C 4 4. Para cada uno de los elementos C 2, C 2 'y C 2” hay dos operaciones hasta que se alcanza la identidad. C 2 1, C 2 2, C 2 1 ', C 2 2', C 2 1”, C 2 2”. El C 4 4, el C 2 2, el C 2 2 ', y el C 2 2” son lo mismo que la identidad y por lo tanto no los consideramos. Además podemos ver que el C 4 2 es lo mismo que el C 2 1. Esto se debe a que los ejes C 4 y C 2 están en la misma ubicación, y girar dos veces alrededor de 90° es lo mismo que rotar una vez alrededor de 180°. Por convención eliminamos la operación asociada al orden superior, así la C 4 2. La notación general sería entonces: C 4 1, C 4 3, C 2 1, 2 C 2 1 '2 C 2 1” (Fig. 2.1.5).
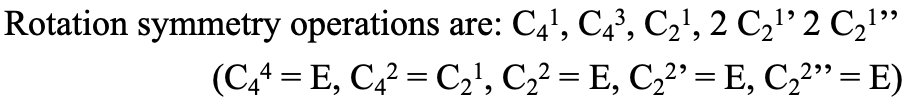
Las operaciones de reflexión (σ)
Veamos las operaciones de reflexión que se llevan a cabo alrededor de planos de reflexión, o planos de espejo. Los planos espejo tienen el símbolo de Schoenflies σ. Cuando realizamos una operación de reflexión, entonces movemos cualquier punto del objeto al otro lado del plano espejo. Hay dos tipos de planos de espejo, los llamados planos de espejo horizontales y planos de espejo verticales. Un plano de espejo horizontal siempre se sitúa perpendicular al eje principal. Por ejemplo, en la molécula BH 3 representada hay un plano espejo horizontal que se sitúa perpendicular a un eje principal C 3 (Fig. 2.1.6). Un plano de espejo horizontal tiene el símbolo de Schoenflies σ h.
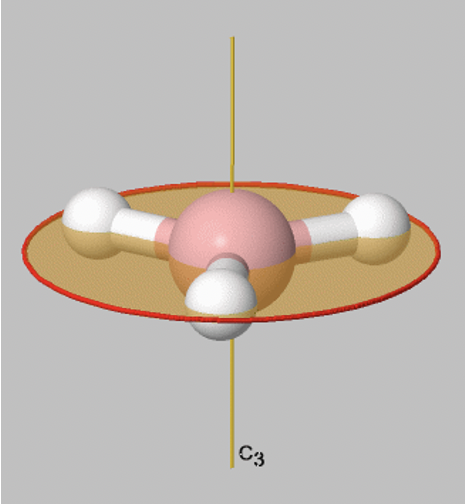
Un plano de espejo vertical tiene la propiedad de que contiene el eje principal, esto significa que es parte del eje principal. Se denota σ v. La molécula BH 3 tiene tres ejes verticales que pasan a través de los tres enlaces B-H. Se puede ver que cada uno de ellos contiene el eje principal C 3 (Fig. 2.1.7). Los tres planos de espejo verticales son conjugados, y por lo tanto no se distinguen por primos. Podemos escribir un coeficiente 3 delante del símbolo σ v para indicar que hay tres planos especulares verticales conjugados.
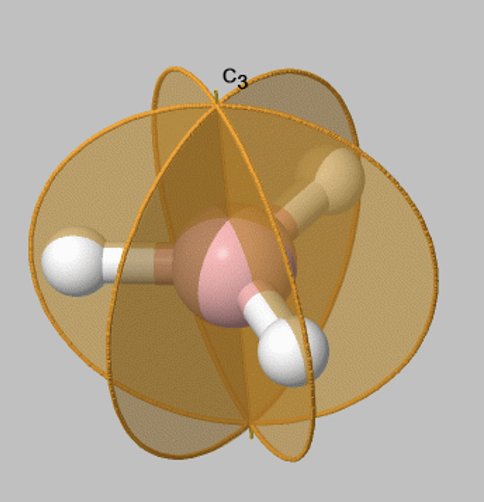
Ahora veamos cuántas operaciones de simetría están asociadas con un plano especular en particular. Afortunadamente, las cosas son simples aquí: Solo hay una operación de reflexión asociada a un plano espejo. Esto porque reflejar dos veces en un plano espejo produce la identidad E: σ v 2 =E. más generalmente, cuando reflejamos n veces, y n es un número par entonces esto es lo mismo que la identidad o, σ v n =E (n es par). Cuando n es impar el reflejo n veces es el mismo a reflejando solo una vez o, σ v n =σ v 1 (n=impar).
El plano espejo horizontal de la molécula BH 3 merece un comentario adicional. Llevar a cabo la reflexión horizontal no cambia la posición de ningún átomo. Es importante entender por qué la operación sí existe a pesar de que no cambia la posición de ningún átomo. El criterio no es si se cambia la posición de un átomo, sino si cambia la posición de los puntos en el objeto. En el caso de la molécula BH 3 la parte de la molécula que se encuentra por encima del plano espejo se ubicará por debajo del plano espejo después de que se haya realizado la operación de reflexión. Viceversa cualquier parte de la molécula que anteriormente estaba por debajo del plano espejo se ubicará por encima del plano espejo después de que se haya realizado la operación de reflexión. Por ejemplo, la mitad inferior del átomo B con estar por encima del plano espejo, y la mitad por encima del plano estará por debajo del plano después de la ejecución de la operación de reflexión.
Al igual que las rotaciones apropiadas no conjugadas se distinguen por primos, también los planos especulares verticales no conjugados deben distinguirse por primos. Cuanto menor sea el número de enlaces que contiene el plano espejo vertical, mayor es el número de primos.
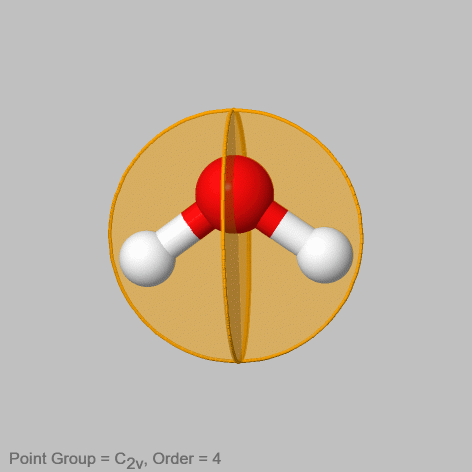
Por ejemplo en la molécula de agua (Fig. 2.1.8) hay dos planos especulares verticales no conjugados. Uno contiene los dos enlaces O-H, el otro se coloca perpendicular al primer plano espejo. Es fácil ver que estos dos planos espejo no moverán los puntos en el átomo de manera equivalente, y por lo tanto no son conjugados. El primer plano espejo no cambia la posición de ningún átomo, mientras que el segundo intercambia las posiciones de los dos átomos de hidrógeno. Por lo tanto, el segundo plano espejo que no contiene ningún enlace O-H obtiene un primo el que contiene los enlaces O-H no obtiene un primo.
Planos de Reflejo Diedro (σ d)
Un caso especial de un plano de espejo vertical es un plano de espejo diedro, denotado σ d. Un plano de espejo diedro bisecta el ángulo entre dos ejes conjugados C2.
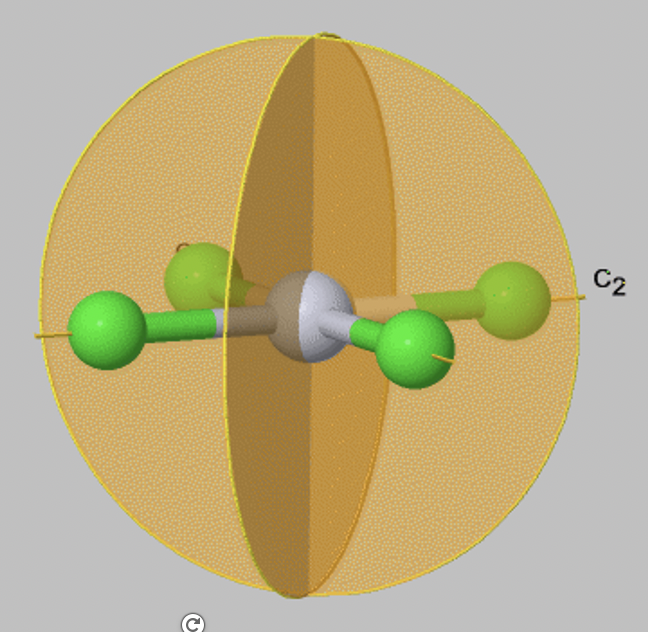
Por ejemplo, en el anión PtcL 4 2- (Fig. 2.1.9) hay dos planos especulares verticales que bisecan el ángulo entre los dos ejes conjugados C2 que pasan a través de los enlaces Pt-Cl. Por lo tanto, estos planos de espejo son planos especulares verticales σ d.
La Operación de Inversión (i)
Veamos a continuación la operación de inversión que está simbolizada por un símbolo de Schoenflies i. El elemento de simetría asociado a una inversión, es el centro de inversión, también llamado centro de simetría. Se trata de un solo punto. Cuando se realiza una operación de inversión, entonces cada punto del objeto se mueve a través del centro de inversión hacia el otro lado. Cada coordenada en el objeto (x, y, z) se invierte en las coordenadas (-x, -y, -z).
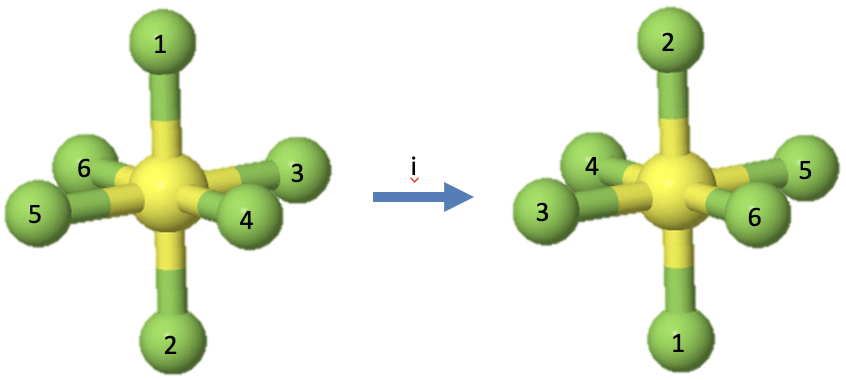
Por ejemplo, la molécula octaédrica SF 6 tiene un centro de inversión en el centro de la molécula (Fig. 2.1.10). Cuando se realiza la operación de inversión, entonces cada átomo de flúor se mueve a través del centro de inversión hacia el otro lado. Esto significa que los átomos de flúor 1 y 2 intercambian sus posiciones, los átomos de flúor 3 y 5 intercambian sus posiciones, y también los átomos de flúor 4 y 6. El átomo de azufre no cambia su posición. Solo hay una operación de inversión asociada a cada centro de inversión. Invertir dos veces, o más generalmente, un número entero de dos veces produce la identidad. Invertir un número impar de veces es lo mismo que invertir una vez.
La Operación Rotación-Reflexión (S n)
La operación de rotación-reflexión S n es la operación de simetría más compleja. Se lleva a cabo en dos etapas. En primer lugar, se realiza una rotación alrededor de un eje impropio. El ángulo está determinado por el orden n del eje incorrecto, y es 360°/n. Este eje se denomina impropio, ya que el objeto no necesita superponer el objeto original después de la rotación. Lograr la superposición requiere el segundo paso que es el reflejo en un plano espejo que se encuentra perpendicular al eje impropio. Sólo después del segundo paso se completa la operación. La presencia de la rotación-reflexión no requiere un eje de rotación adecuado o un plano espejo regular σ para existir, sin embargo tampoco excluye su existencia.
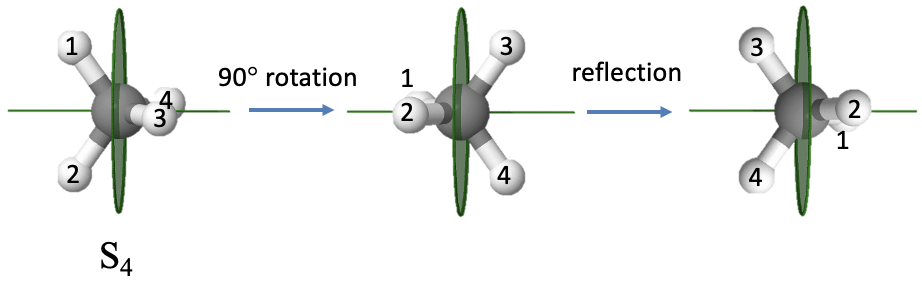
Un ejemplo de una molécula con un eje impropio es la molécula de metano (Fig. 2.1.11). Tiene un eje S 4 impropio. El eje bisecta el ángulo de unión tetraédrico H-C-H. El orden del eje es cuatro lo que requiere que giremos 90° alrededor de este eje. Se puede ver que después de llevar a cabo la rotación, la molécula no superpone a la molécula original. Solo después de reflejar la molécula girada en un plano espejo que se coloca perpendicular al eje impropio, la molécula se superpone a la molécula original.
Propiedades de la Operación Rotación-Reflexión (S n)
La rotación-reflexión tiene una serie de propiedades interesantes. Uno de ellos es que una operación S 1 es lo mismo que una reflexión. Esto se debe a que el orden 1 implica una rotación alrededor de 360° que produce la identidad, y todos los puntos dentro del objeto están en su posición original. Esto es lo mismo que si no hubiéramos girado en absoluto. Esto significa que en realidad solo hicimos el segundo paso, la reflexión, y por lo tanto la S1 es idéntica a una reflexión “regular”. La segunda propiedad es que una operación S 2 es lo mismo que una inversión. Cuando gira alrededor de 180° y luego refleja perpendicular al eje de rotación incorrecto, las posiciones de los puntos en el objeto cambian exactamente de la misma manera que lo hacen cuando se invierta a través de un centro de inversión.
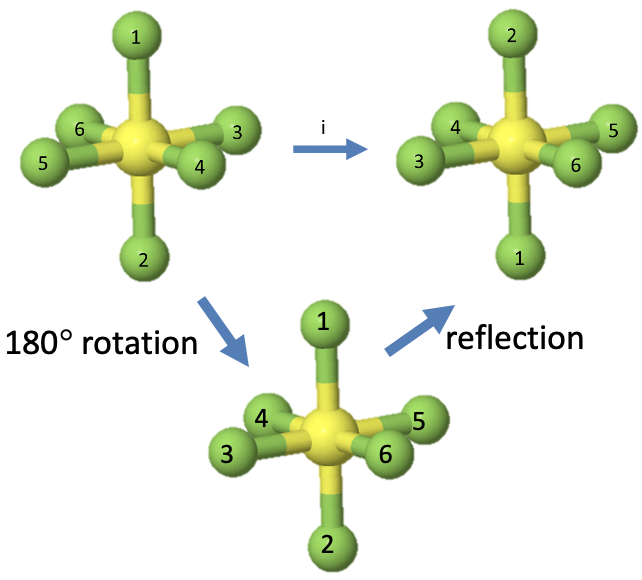
Busque por ejemplo de nuevo la molécula SF 6 (Fig. 2.1.12) que tiene un centro de inversión en el centro del átomo. Anteriormente vimos que cuando realizamos la inversión, los átomos 1 y 2 intercambian su posición, y así lo hacen los átomos 3 y 5, así como los átomos 4 y 6. Llevemos a cabo la rotación-reflexión, y veamos si los átomos cambian de la misma manera. En primer lugar giramos 180° alrededor de un eje que atraviesa los átomos 1 y 2. Esto deja inalteradas las posiciones de los átomos 1 y 2, pero intercambia las posiciones de los átomos 3 y 5, así como los átomos 4 y 6. A continuación debemos hacer una reflexión en un plano que se sitúa perpendicular al eje impropio. Es el plano definido por los átomos 3, 4, 5 y 6. La reflexión en este plano no cambia las posiciones de los átomos 3, 4, 5 y 6, sino que intercambia las posiciones de los átomos 1 y 2, que se encuentran por encima y por debajo del plano, respectivamente. Podemos ver que las posiciones de los átomos son las mismas que después de la inversión.
El hecho de que podamos expresar una reflexión mediante una reflexión de rotación S 1, y una inversión por una reflexión de rotación S 2 significa que la reflexión y la inversión no son operaciones de simetría independientes, y no las necesitaríamos. La simetría de un objeto podría describirse completamente por la identidad, las rotaciones adecuadas y las reflexiones de rotación. Sin embargo, por convención, utilizamos reflexiones e inversiones en lugar de S 1 y S2, simplemente porque es más fácil para la mente humana realizar operaciones de 1 paso, en lugar de operaciones de 2 pasos.
Las rotaciones incorrectas tienen diferentes propiedades dependiendo de si el orden del eje es par o impar. Para órdenes pares, la presencia de un eje rotacional incorrecto S n implica que también debe haber un eje de rotación adecuado con un orden n/2. Para ejes incorrectos de órdenes pares n la identidad se produce después de n rotación-reflexiones (Fig. 2.1.13).
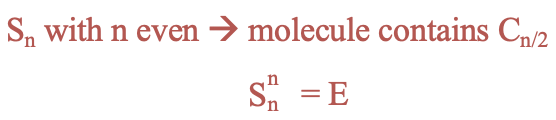
Para ejes impropios de orden impar n, llevar a cabo la rotación-reflexión n veces es lo mismo que realizar una reflexión en un plano espejo horizontal. Necesitamos hacer la rotación-reflexión 2n veces para alcanzar la identidad (Fig. 2.1.4).
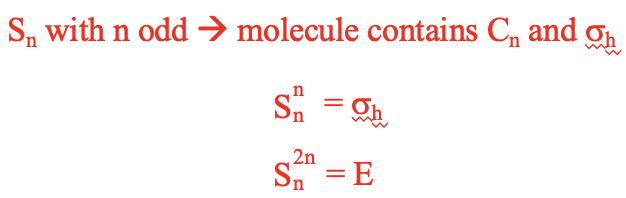
Reflexiones de rotación de PF 5 (un ejemplo con orden impar)
Vamos a mostrar estas propiedades usando dos ejemplos. Veamos primero un ejemplo con una rotación impropia de orden impar. La molécula PF 5 tiene forma piramidal trigonal con tres átomos F en el plano ecuatorial, y dos átomos F adicionales por encima y por debajo del plano. Los átomos F han sido numerados del 1 al 5 como lo indican los subíndices que siguen al símbolo del elemento (Fig. 2.1.15). El PF 5 tiene un eje rotacional incorrecto S3 que se coloca perpendicular al plano ecuatorial pasando por los enlaces P-F 1 y P-F 2. Realicemos las operaciones de simetría S 3 paso a paso y veamos cómo se mueven los átomos.
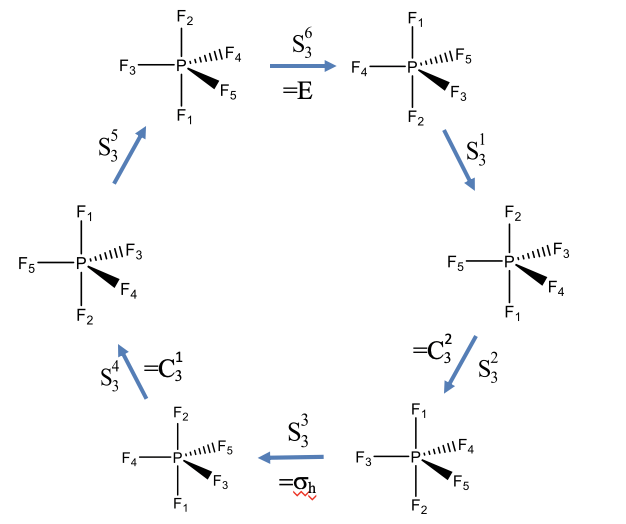
Esperaríamos que después de llevar a cabo el operativo seis veces se produzca la identidad. Después de tres reflexiones de rotación, esperaríamos que el objeto se haya movido de la misma manera que lo haría un plano espejo horizontal. Después de la primera rotación-reflexión los átomos F 1 y F 2 han intercambiado sus posiciones, y los tres átomos F en el plano ecuatorial han sido girados 120 grados en sentido antihorario. El átomo F 5 ocupa ahora la posición del F 4, el F 4 se ha girado a la posición del F 3, y el F 3 se ha movido a la posición del F 5. La segunda operación S3 vuelve a intercambiar los átomos F 2 y F 1, y gira 120° los átomos F restantes. Ahora los átomos F 5 apuntan hacia nosotros, el átomo F 4 apunta lejos de nosotros, y los átomos F 3 están en el plano de papel. Al realizar la operación una tercera vez, nuevamente se intercambian los F 1 y F 2 y gira los F 3, F 4 y F 5 en sentido antihorario 120°. Ahora comparemos la posición de los átomos con las posiciones de los átomos de la molécula con la que empezamos. Vemos que la posición de los átomos F ecuatoriales son las mismas que al principio, pero la posición de los átomos F 1 y F 2 axiales se han intercambiado hacia arriba. Esto equivale a una reflexión en un plano especular horizontal ubicado dentro del plano ecuatorial. Este plano espejo horizontal sólo cambiaría los átomos F axiales, pero no movería los ecuatoriales. La operación S 3 4 vuelve a cambiar la posición de los átomos F 1 y F 2, y gira los átomos F ecuatoriales 120° en sentido antihorario. Ahora, F 4 apunta hacia nosotros, F 3 apunta a distancia, y F 5 está en el plano de papel. Después de la quinta rotación-reflexión F 1 y F 2 se intercambian nuevamente para que F 1 esté por debajo y F 2 esté por encima del plano ecuatorial. Los átomos F 3, F 4 y F 5 se rotan para que F 3 esté en el plano de papel, F 5 apunte hacia nosotros y F 4 apunte lejos de nosotros. La sexta rotación-reflexión vuelve a cambiar F 1 y F 2, y gira los otros átomos de F alrededor de 120° en sentido antihorario. Ahora podemos ver que la molécula producida es la misma que la que iniciamos, y la identidad se ha producido.
También es de destacar que la operación S 3 2 y la S 3 4 pueden expresarse mediante operaciones más simples, es decir, C 3 2 y C 3 1 operaciones de rotación adecuadas. Podemos entender esto considerando que una operación S 3 2 requiere que reflexionemos dos veces, y reflejar dos veces es como no reflejar en absoluto. De manera efectiva, solo tenemos dos rotaciones alrededor de 120° lo que equivale a C 3 2. De igual manera, la operación S 3 4 requiere reflejar cuatro veces, lo que es lo mismo que no reflejar en absoluto. Así, efectivamente, solo giramos cuatro veces alrededor de 120°. Esto es lo mismo que girar solo una vez alrededor de este ángulo, lo que equivale a una operación C 3 1.
Usando consideraciones similares, también podemos entender por qué la operación S 3 3 es equivalente a a σ h. En este caso, giramos 3 x 120° = 360°, y rotar alrededor de 360° es lo mismo que no rotar en absoluto. Además, realizamos una reflexión en tres ocasiones. Reflejar un número impar de veces es lo mismo que reflejar una sola vez. Así, en general, llevamos a cabo efectivamente una sola reflexión únicamente.
En general, solo las operaciones S 3 1 y S 3 5 son únicas, todas las demás pueden ser expresadas por otras operaciones más simples.
Rotación-Reflexiones de CH 4 (un ejemplo con orden par)
Ilustremos las propiedades de un eje rotacional incorrecto con orden par usando el metano del ejemplo (Fig. 2.1.16).
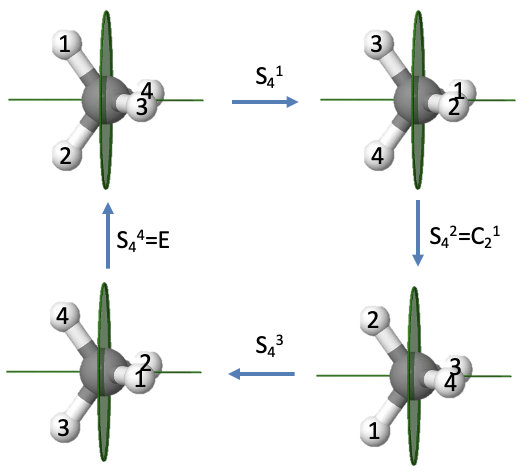
Anteriormente vimos que la molécula de metano tiene un eje S 4 impropio. Al ejecutar la operación de simetría una vez se mueven los átomos H 1 y 2 hacia la derecha, por lo que el átomo 1 apunta hacia la parte posterior y el átomo 2 apunta hacia el frente. Después de la segunda rotación-reflexión los átomos 1 y 2 se reflejan de nuevo hacia el lado izquierdo, pero debido a que hemos girado dos veces 90° el átomo 2 puntos hacia arriba, y el átomo 1 apunta hacia abajo. De igual manera, los átomos 3 y 4 se reflejan de nuevo hacia el lado derecho, pero el átomo cuatro puntos hacia nosotros y el átomo 3 apunta hacia atrás. Después de tres reflexiones de rotación, los átomos 1 y 2 están nuevamente en el lado derecho con el átomo 2 apuntando hacia atrás y el átomo 1 apuntando hacia el frente. Los átomos 3 y 4 están a la izquierda con el átomo 4 apuntando hacia arriba y el átomo 3 apuntando hacia abajo. Después de que la operación se lleva a cabo en cuatro ocasiones, todos los átomos vuelven a estar en su posición original, es decir, se ha producido la identidad. Esto es lo que esperábamos para una rotación inadecuada de orden par. Podemos ver además que la operación S 4 2 es la misma que una operación C 2. Girar dos veces aproximadamente 90° es lo mismo que rotar alrededor de 180°. Reflexionar dos veces es lo mismo que no reflexionar en absoluto. Por lo tanto, efectivamente, solo giramos 180° que es lo mismo que hace una operación C 2 1. Debido a que un S 4 2 puede ser expresado por un C 2 1, y un S 4 4 es lo mismo que la identidad, solo el S 4 1 y el S 4 3 son operaciones de simetría únicas.
La simetría de una molécula
Ahora hemos discutido todo tipo de elementos de simetría y operaciones que pueden existir en un objeto. A continuación, pensemos en cómo podemos definir la simetría global de un objeto. La simetría general de un objeto se define como la suma de todas las operaciones de simetría para este objeto. Si dos objetos tienen exactamente los mismos elementos de simetría y operaciones entonces su simetría es la misma. Usando el lenguaje matemático de la teoría de grupos, la teoría matemática para la simetría, podemos decir que pertenecen al mismo grupo de puntos. El grupo de puntos de nombre proviene del hecho, que tiene al menos un punto invariante. El número de operaciones de simetría que pertenecen a un grupo de puntos se denomina el orden del grupo de puntos. Veamos a continuación qué diferentes grupos puntuales conocemos y cómo podemos clasificarlos sistemáticamente.