2.2: Grupos de puntos
- Page ID
- 70125
Los grupos de puntos de simetría baja
C Grupo de 1 Punto
En general, dividimos los grupos de puntos en tres categorías principales: grupos de puntos de simetría alta, grupos de puntos de simetría baja, grupos de puntos diedros y grupos de puntos rotacionales. Comencemos con los grupos de puntos de baja simetría. Como su nombre lo dice, estos grupos de puntos sólo tienen pocos elementos de simetría y operaciones. El grupo de puntos C1 es el grupo de puntos con la simetría más baja. Las moléculas que pertenecen a este grupo puntual solo tienen la identidad como elemento de simetría.
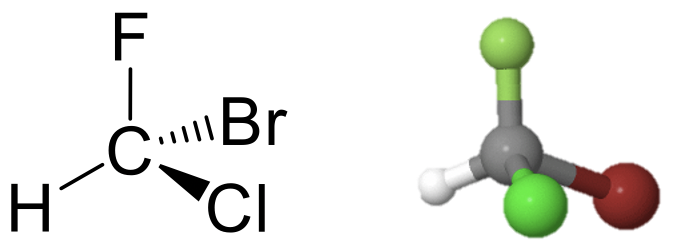
Un ejemplo es la molécula de bromocloroflurometano (Fig. 2.2.1). No tiene elemento de simetría, sino la identidad. El nombre C 1 proviene del elemento de simetría C 1. Una operación C 1 es lo mismo que la identidad.
C s Grupo de puntos
El grupo de puntos C s tiene un plano espejo además de la identidad. Un ejemplo es la molécula de 1,2-bromocloroeteno (Fig. 2.2.2).
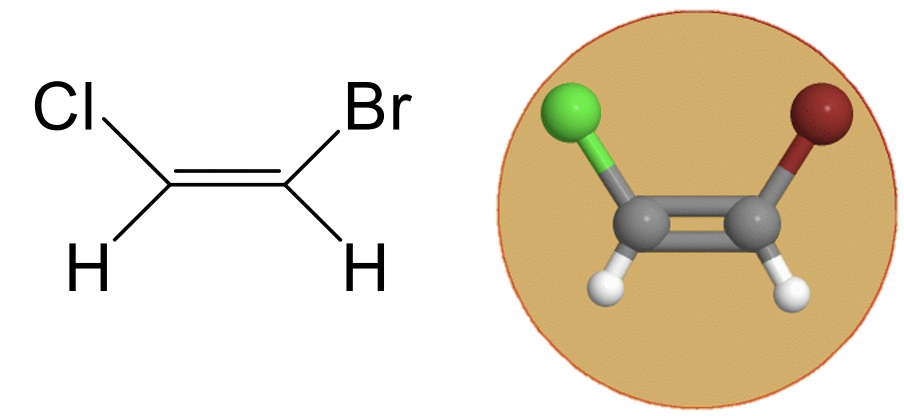Figura 2.2.2 Grupo de puntos C de 1, 2-bromocloroeteno (Atribución: symotter.org/gallery)Esta es una molécula plana y el plano espejo está dentro del plano de la molécula. Este plano espejo no mueve ningún átomo cuando se realiza la operación de reflexión, sin embargo existe porque cualquier punto de la molécula por encima del plano espejo se encontrará debajo del plano espejo después de la ejecución de la operación. Viceversa, cualquier punto debajo del plano espejo estará por encima del plano espejo. Este plano de espejo no tiene una designación de plano de espejo vertical u horizontal porque no existen ejes de rotación adecuados.
Grupo de Puntos C i
El grupo puntual C i tiene la inversión como único elemento de simetría además de la identidad. El grupo puntual C i a veces también se llama S 2 porque una S 2 rotación-reflexión inadecuada es lo mismo que una inversión. Un ejemplo es el 1,2-dibromo 1,2-dicloro etano (Fig. 2.2.3).
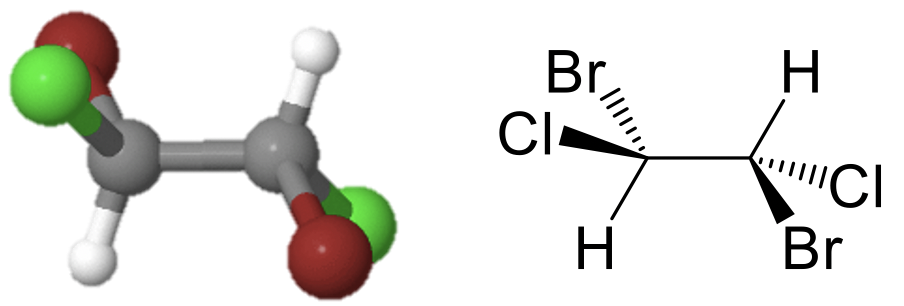
Esta molécula parece bastante simétrica, pero tiene el centro de inversión en medio del enlace carbono-carbono como único elemento de simetría. Al ejecutar la operación de inversión, los dos carbonos intercambian sus posiciones, y también lo hacen los dos átomos de bromo, los dos corinos y los dos átomos de hidrógeno.
Los grupos de puntos de alta simetría
Los elementos de simetría de los grupos de puntos de alta simetría se pueden entender más fácilmente cuando se entienden primero las propiedades de los sólidos platónicos. Los sólidos platónicos son poliedros hechos de polígonos regulares. En un sólido platónico, todas las caras, aristas y vértices (esquinas) son equivalentes a simetría. Veremos que esta es una propiedad que puede ser utilizada para entender los elementos de simetría en grupos de puntos de simetría alta. Solo hay cinco posibilidades para hacer sólidos platónicos a partir de polígonos regulares (Fig. 2.2.4).
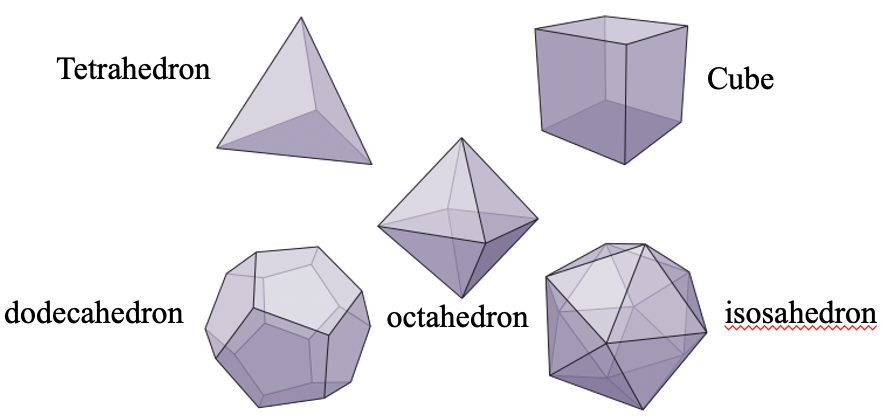
La primera posibilidad es construir un tetraedro a partir de cuatro triángulos regulares. El segundo sólido platónico es el octaedro compuesto por ocho triángulos regulares. La tercera posibilidad es el icosaedro hecho de veinte triángulos. Además, se pueden conectar seis cuadrados para formar un cubo, y doce pentágonos se pueden conectar para formar un dodecaedro. No hay posibilidades de conectar otros polígonos regulares como hexágonos para hacer un sólido platónico.
El icosaedro es el más complejo de todos los sólidos platónicos. Si quieres ver y estudiar un icosaedro desde afuera y por dentro, hay uno para estudiar en el patio de recreo del Allentown Cedar Beach Park, en Allentown, Pensilvania.
El Grupo T d Point
El tetraedro, así como las moléculas tetraédricas y aniones como CH 4 y BF 4 - pertenecen al grupo de puntos de alta simetría T d. Busquemos los elementos de simetría y las operaciones de simetría que pertenecen al grupo de puntos T d. Primero, no debemos olvidar la operación de identidad, E. A continuación, es útil buscar los ejes principales.
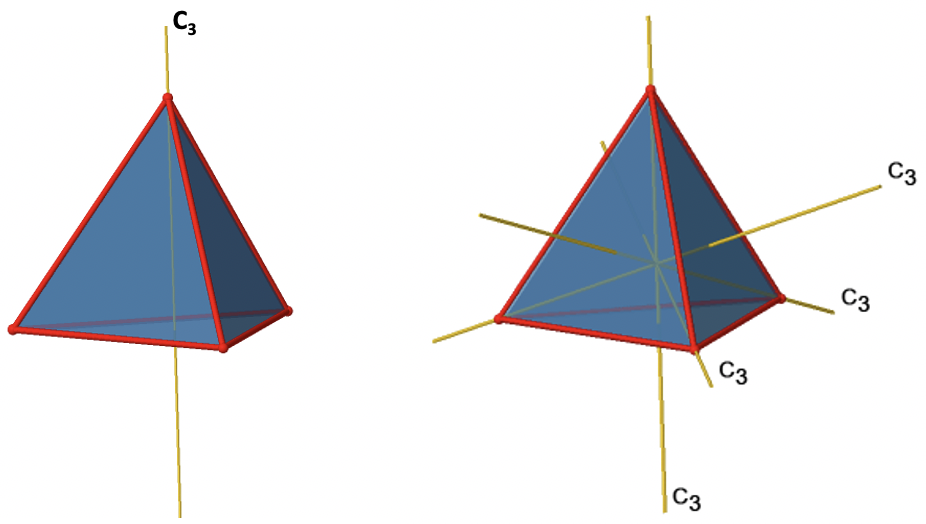
El tetraedro tiene cuatro ejes C 3 principales (Fig. 2.2.6). Es una propiedad de los grupos de puntos de alta simetría que tienen más de un eje principal. Los ejes C 3 atraviesan los vértices del tetraedro. Debido a que cada eje C 3 pasa por un vértice, hay cuatro vértices, y sabemos que en un sólido platónico todos los vértices son equivalentes a simetría, podemos entender que hay cuatro ejes C 3. ¿Cuántas operaciones únicas de C 3 están asociadas con estos ejes? Después de tres rotaciones alrededor de 120° llegamos a la identidad. Por lo tanto C 3 3 =E, y solo necesitamos considerar la rotación C 3 1 y C 3 2 alrededor de 120 y 240° respectivamente. Debido a que hay cuatro ejes C 3, hay cuatro operaciones C 3 1 y cuatro C 3 2 y ocho operaciones C 3 en general. Podemos expresarlo escribiendo los números respectivos como coeficientes frente al símbolo de Schoenflies para las operaciones (Fig. 2.2.7).
Además de los ejes C 3 hay ejes C 2 (Fig. 2.2.8).
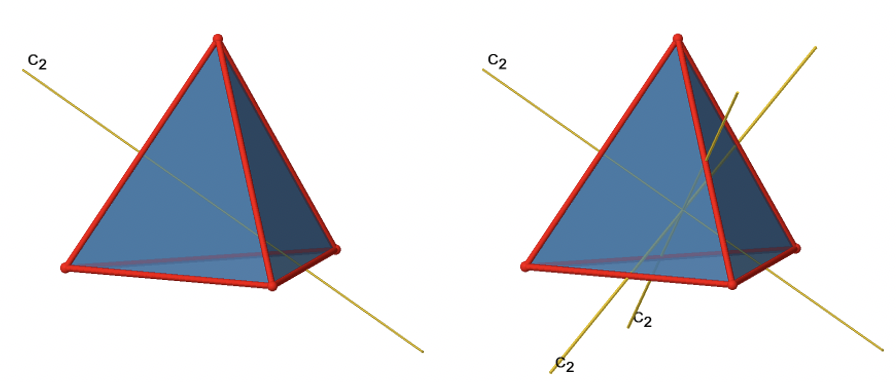
Se puede ver que un eje C 2 pasa por dos bordes opuestos en el tetraedro. Debido a que un tetraedro tiene seis bordes, y cada eje C 2 pasa por dos bordes hay 6/2=3 ejes C 2. Solo hay una operación de simetría C 2 por eje C 2 porque producimos la identidad ya después de dos rotaciones. Por lo tanto, hay tres operaciones C 2 1 en general (Fig. 2.2.9).
Además, el grupo de puntos T d tiene S 4 reflexiones de rotación inadecuadas. Al igual que los ejes C 2, pasan por el medio de dos bordes opuestos. Esto también significa que están superponiendo los ejes C 2. Debido a que hay seis bordes, y dos S 4 ejes por borde hay 6/2=3 S 4 ejes (Fig. 2.2.10).
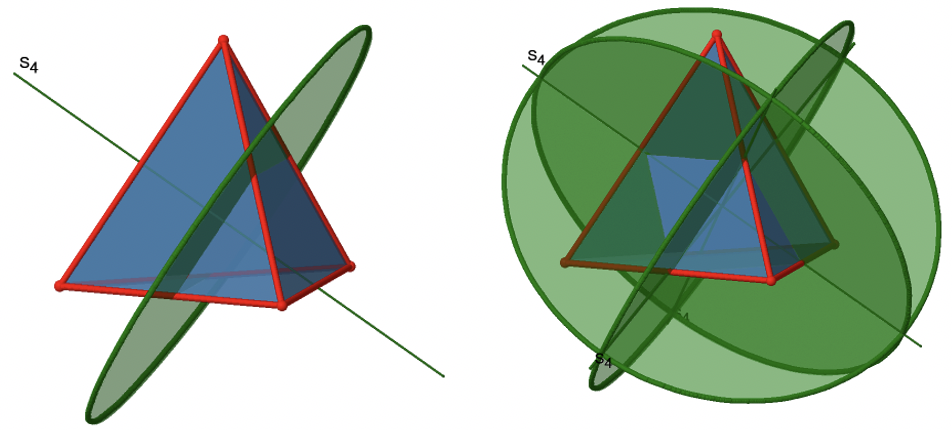
¿Cuántas operaciones están asociadas con estos ejes S 4? El orden de los ejes es parejo, y por lo tanto necesitamos cuatro operaciones S 4 para producir la identidad. La operación S 4 2 es la misma que una operación C 2 1 porque reflejar dos veces equivale a no reflejar en absoluto, y girar dos veces 90° es lo mismo que rotar alrededor de 180°. Por lo tanto, en general, solo las operaciones S 4 1 y S 4 3 son operaciones únicas. S 4 2 y S 4 4 pueden expresarse mediante las operaciones más simples C 2 1 y E respectivamente. Debido a que hay 3 S 4 ejes, hay tres S 4 1 y tres S 4 3 operaciones. En general hay seis operaciones S 4 (Fig. 2.2.11).
También hay planos de espejo (Fig. 2.2.11). Los planos contienen un solo borde del tetraedro, biseccionando así el tetraedro. Hay seis bordes en un tetraedro, y por lo tanto hay 6/1=6 planos espejo.
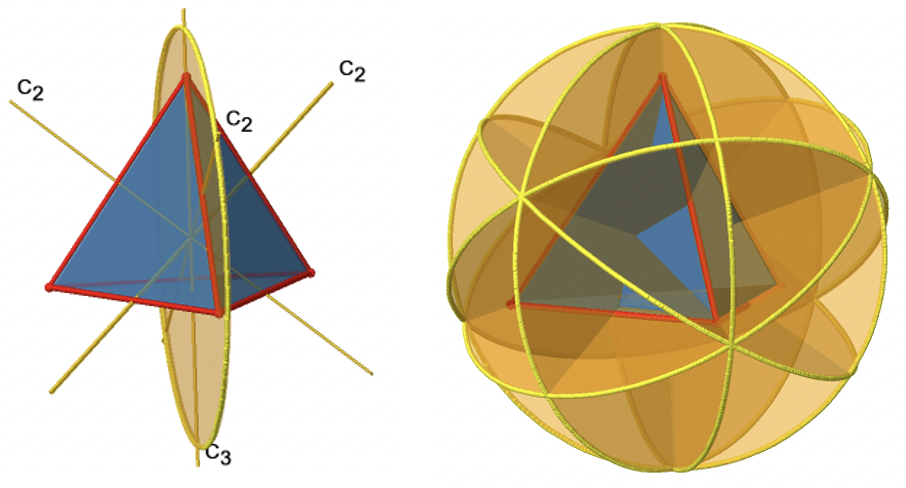
Estos planos son planos diedros porque cada plano contiene un eje principal C 3 y se biseca el ángulo entre dos ejes C 2. En general, hay tres ejes C 2 y tres operaciones C 2. Hay una operación de reflexión por plano de espejo porque reflejar dos veces produce la identidad. Por lo tanto, hay seis operaciones de reflexión σ d (Fig. 2.2.12, derecha y Fig. 2.2.13).
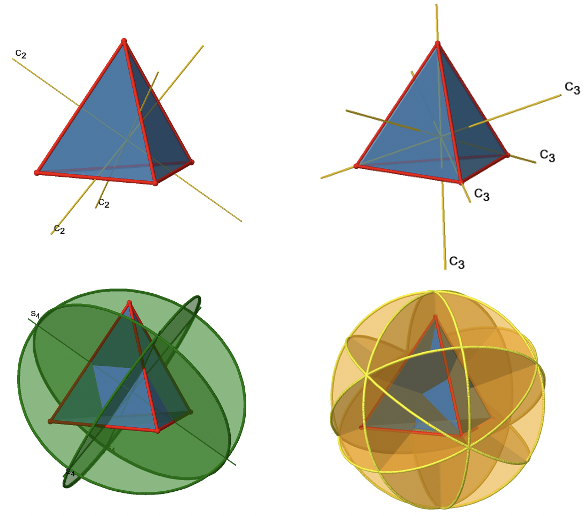
En suma (Fig.2.2.14 y 2.2.15) podemos denotar la simetría global del grupo de puntos T d de la siguiente manera: E, 8C 3, 3C 2, 6S 4, 6σ d. En detalle las operaciones de simetría únicas son E, 4C 3 1, 4C 3 2, 3C 2 1, 3S 4 1, 3S 4 3, 6σ d.
El Subgrupo Rotacional T
El grupo de puntos de alta simetría T es el llamado subgrupo rotacional del grupo de puntos T d. Un subgrupo rotacional es un grupo de puntos en el que todas las operaciones de simetría, excepto la identidad y las rotaciones adecuadas, se han eliminado de un grupo de puntos de alta simetría. Para el grupo puntual T esto deja las operaciones 4C 3, las cuatro C 3 2 y las tres C 2 (Fig. 2.2.17). Se han eliminado las reflexiones de rotación S 4 y los planos de espejo. El grupo de puntos T es raro.
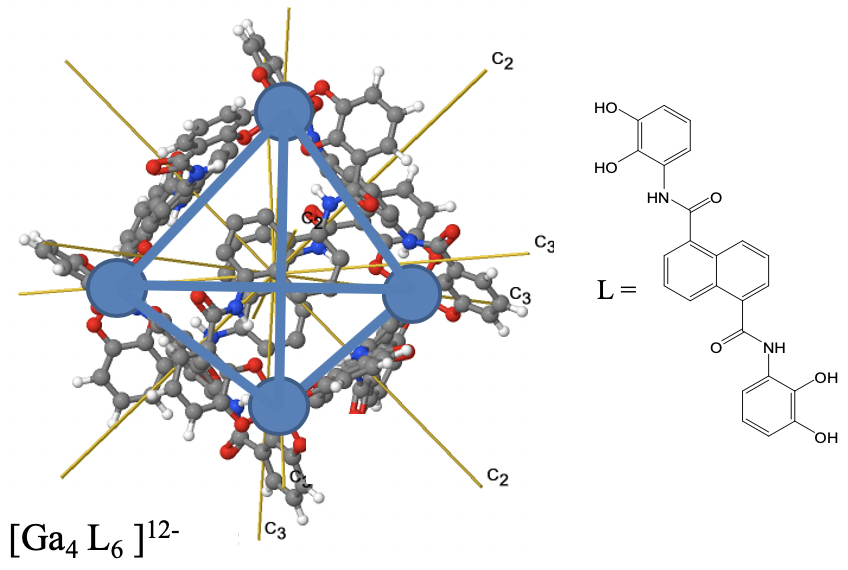
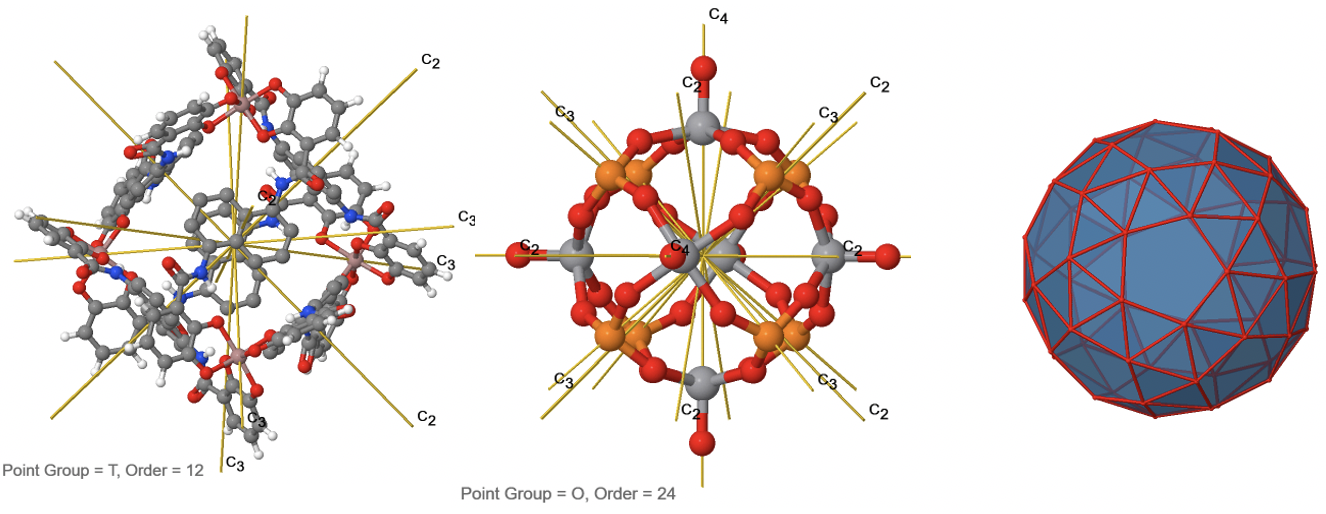
Un ejemplo es la jaula Ga 4 L 6 representada (Fig. 2.2.16). Los átomos de Ga ocupan los vértices de un tetraedro, pero el grupo puntual no es T d sino T debido a la forma de los ligandos que conectan los cuatro átomos de Ga.
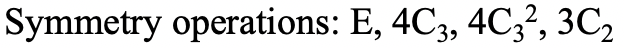
El Grupo de Puntos Octaédricos O h
Otro grupo de puntos de simetría alta es el grupo de puntos O h. Tanto el octaedro como el cubo pertenecen a este grupo puntual a pesar de su forma muy diferente (Fig. 2.2.18). Debido a que pertenecen al mismo grupo de puntos deben tener los mismos elementos de simetría y operaciones. Hay muchas moléculas de forma octaédrica, como la SF 6.
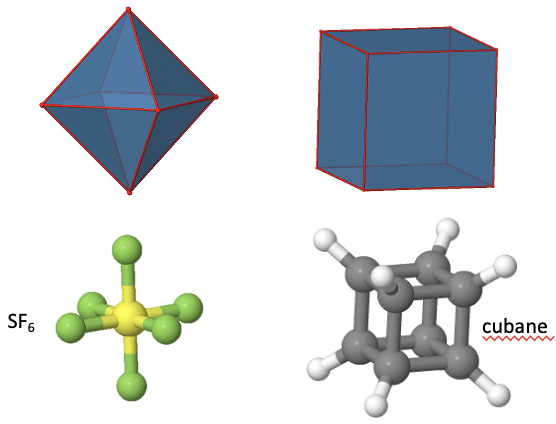
Las moléculas con formas cúbicas son mucho menos comunes, porque una forma cúbica a menudo conduce a una tensión significativa en la molécula. Un ejemplo es el cubane C 8 H 8. Determinemos los elementos de simetría y las operaciones para el grupo de puntos O h usando el ejemplo del octaedro. Si usáramos el cubo, obtendríamos exactamente los mismos resultados.
Hay tres ejes principales C 4 en el octaedro. Pasan por dos vértices opuestos del octaedro (Fig. 2.2.19). Hay tres ejes C 4 porque un octaedro tiene seis vértices que son todos equivalentes a simetría porque el octaedro es un sólido platónico.
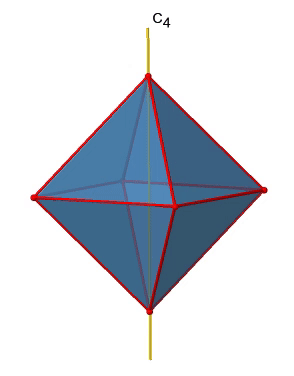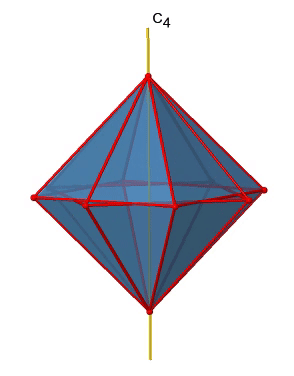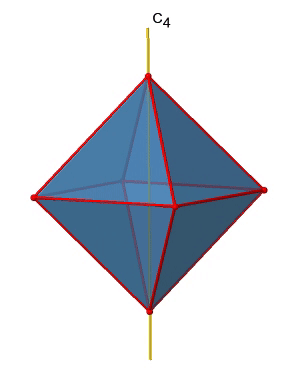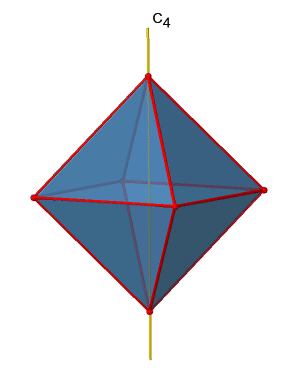
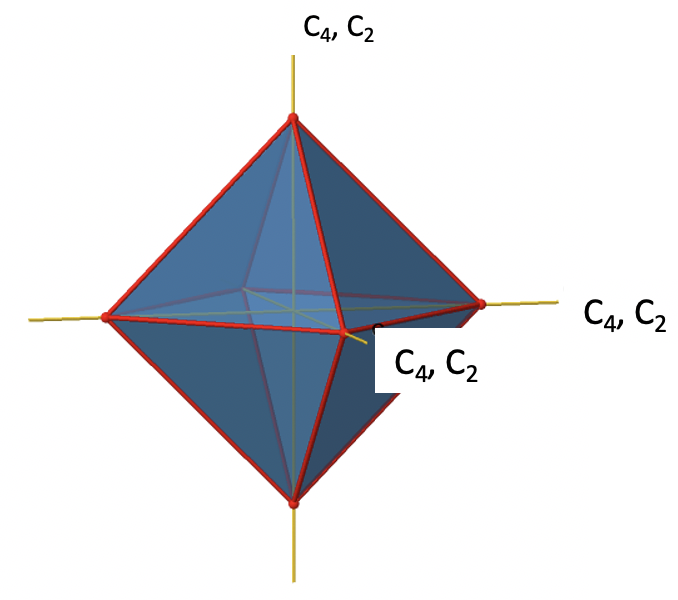
Podemos ver que también hay ejes C 2 donde corren los ejes C 4. Esto se debe a que girar dos veces alrededor de 90° es lo mismo que girar alrededor de 180°. ¿Cuáles son las operaciones de simetría asociadas a estos elementos de simetría? Girar cuatro veces alrededor de 90° usando los ejes C 4 produce la identidad. Por lo que tenemos que considerar las operaciones C 4 1, C 4 2, C 4 3 y C 4 4. ¿Cuántos de estos son únicos? C 4 4 es lo mismo que la identidad, por lo que no es único, además un C 4 2 es idéntico a un C 2 1, y así C 4 2 tampoco es único, y puede ser expresado por la operación más simple C 2 1. Eso deja al C 4 1 y al C 4 3 como las únicas operaciones de simetría únicas. Debido a que tenemos tres ejes C 4, hay operaciones 2x3=6 C 4, en detalle hay 3C 4 1 y tres C 4 3 operaciones. Además, están las tres operaciones C 2 1 pertenecientes a los tres ejes C 2 (Fig. 2.2.20).
Además, hay cuatro ejes C 3 (Fig. 2.2.21). Están atravesando el centro de dos caras triangulares opuestas del octaedro.
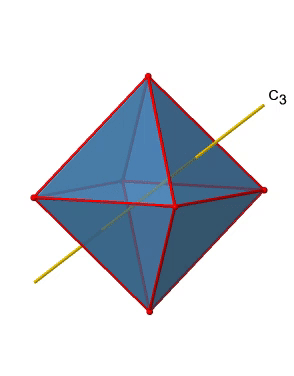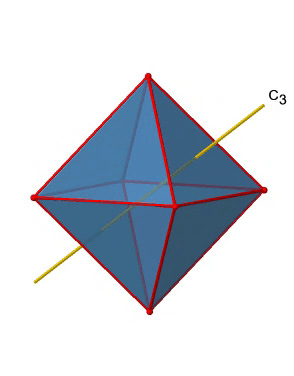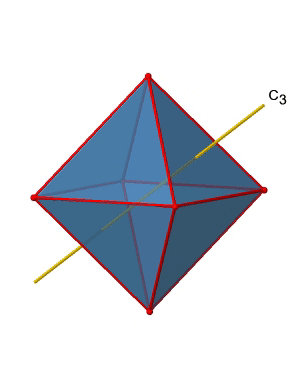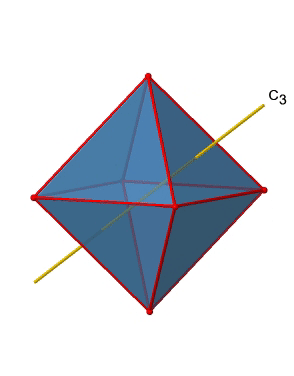
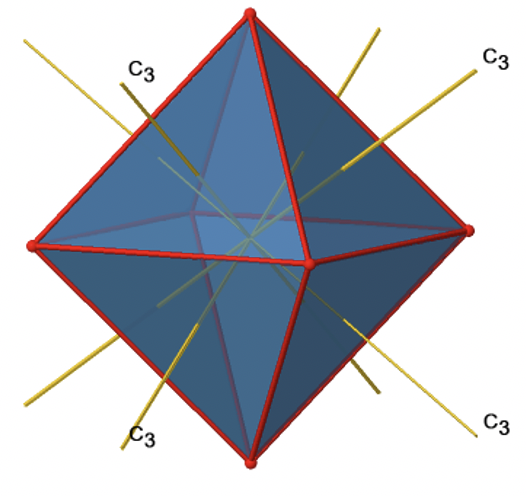
Se ve por encima de un solo eje C 3, y en el lado derecho los cuatro de estos ejes. ¿Cómo podemos entender que hay cuatro ejes? Un octaedro tiene en general ocho caras triangulares, y cada eje C 3 pasa por dos caras opuestas, por lo que hay 8/2=4 ejes C 3. Cada eje C 3 tiene el C 3 1 y el C 3 2 como operaciones de simetría únicas. El C 3 3 es lo mismo que la identidad. Entonces en general tenemos 4x2=8 operaciones, cuatro de ellas son C 3 1, y cuatro de ellas son C 3 2 (Fig. 2.2.22).
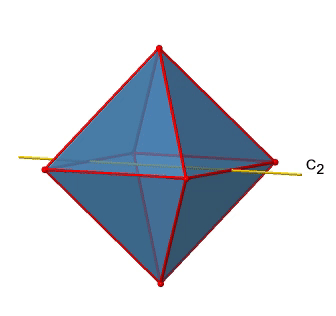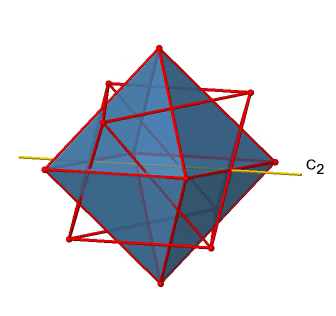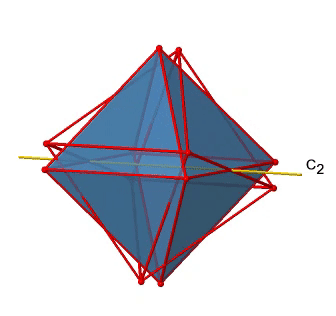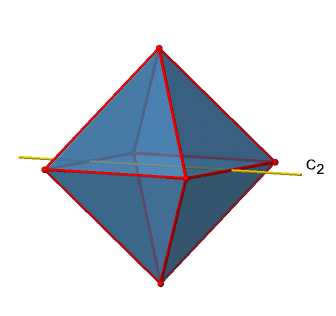
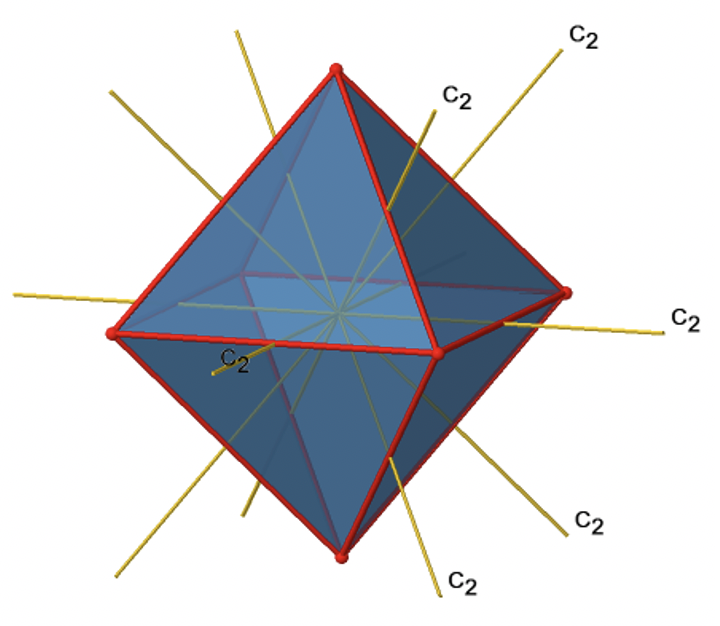
Además de los ejes C 2 que superponen los ejes C 4, hay ejes C 2 'que van a través de dos bordes opuestos del octaedro (Fig. 2.2.23). ¿Cuántos de ellos hay? Un octaedro tiene doce bordes, y debido a que cada C 2 'pasa a través de dos bordes, debe haber 12/2=6 ejes C 2'. Estos ejes tienen primos porque no están conjugados con los ejes C 2 que superponen los ejes C 4. Para cada eje C 2 'solo existe el C 2' 1 como la operación de simetría única, y por lo tanto hay en general 6 operaciones de simetría C 2 '1 (Fig. 2.2.24).
Veamos a continuación los planos espejo (Fig. 2.2.25). Hay planos de espejo horizontales que se colocan perpendiculares a los ejes principales C 4. Se puede ver uno solo de ellos a continuación a la izquierda.
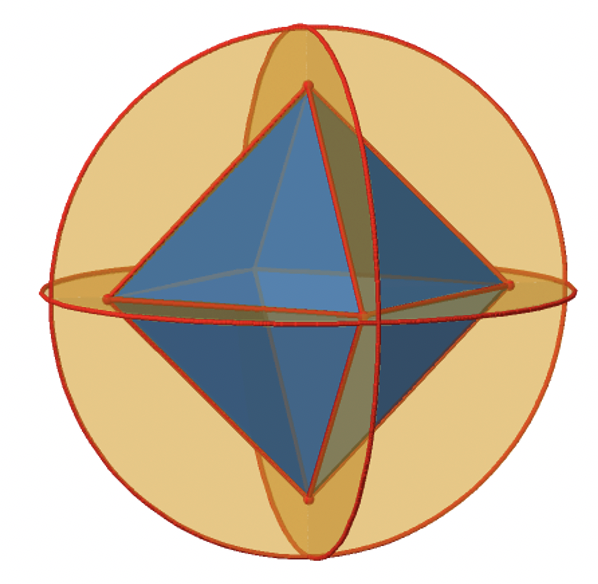
Obsérvese que este plano espejo también contiene dos ejes, además de aquel al que se encuentra perpendicular. Debido a que contiene dos ejes C 4 principales, también tiene propiedades de un plano espejo vertical. Sin embargo, lo llamamos plano espejo horizontal porque se encuentra perpendicular al tercer C 4. Las propiedades horizontales superan a las verticales, por así decirlo. Se puede ver que un solo plano espejo contiene cuatro bordes del octaedro. Debido a que hay doce bordes, hay 12/4=3 planos de espejo horizontales. Hay un plano de espejo por eje principal C 4. Hay tres operaciones de reflexión horizontal porque siempre hay una sola operación de reflexión por plano especular (Fig. 2.2.26).
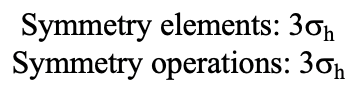
A continuación busquemos planos de espejo vertical (Fig. 2.2.27). Un plano de espejo vertical se representa a continuación a la izquierda.
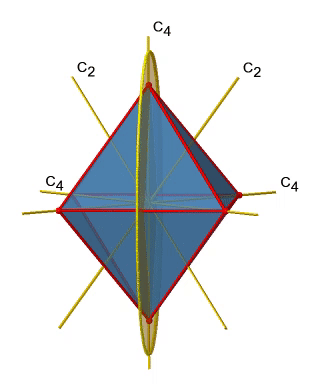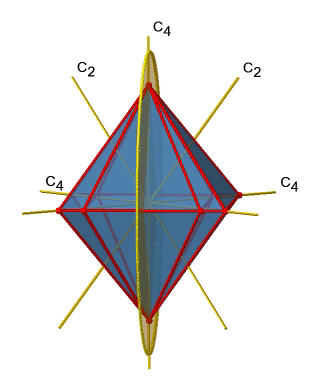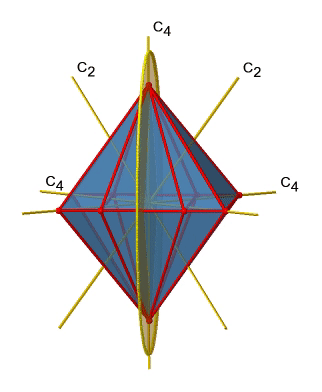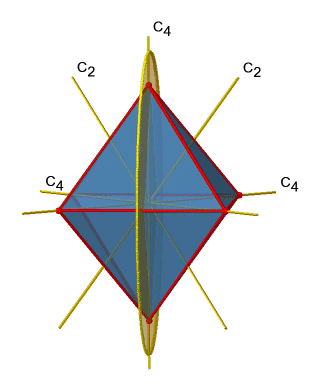
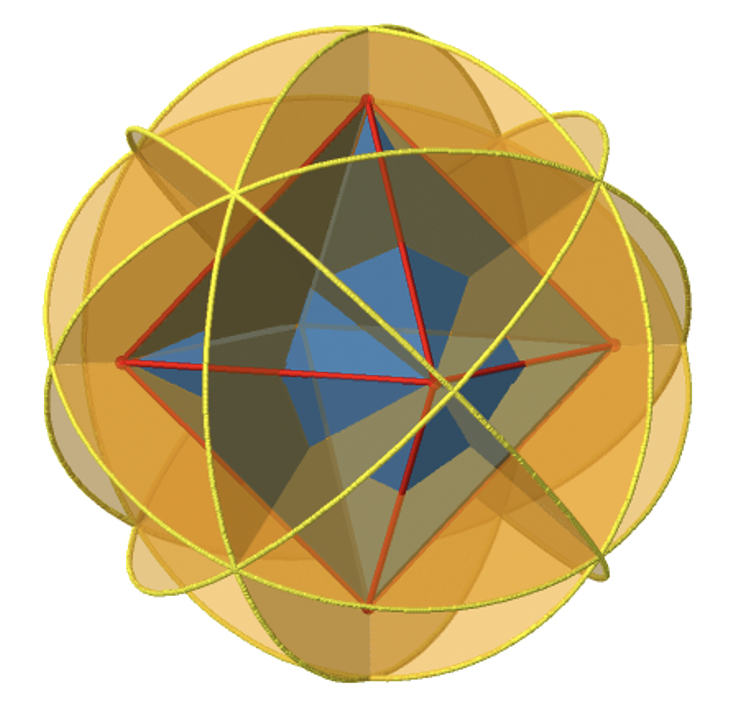
Se puede ver que -a diferencia de los planos de espejo horizontales- no contiene bordes. Más bien, corta a través de dos bordes opuestos. Se puede ver que este plano contiene un eje C 4, pero no se sostiene perpendicular a los otros dos ejes C 4. Por lo tanto, solo tiene las propiedades de un plano espejo vertical. Se puede ver sin embargo, que el plano del espejo biseca el ángulo entre dos ejes C 2 'que también se representa. Esto hace que los planos de espejo verticales planos de espejo diedros, σ d. ¿Cómo podemos de ellos los tenemos? Como se mencionó anteriormente, cada plano de espejo corta a través de dos bordes opuestos. Hay doce bordes en un octaedro, y así hay 12/2=6 planos de espejo diedro. Se pueden ver todos ellos en el lado derecho de la Fig. 2.2.27. Cada plano de espejo está asociado con una operación de reflexión, por lo tanto hay seis operaciones de reflexión diedro (Fig. 2.2.28).
A continuación podemos preguntar si el grupo puntual O h tiene un centro de inversión? ¡Sí, hay uno en el centro del octaedro (Fig. 2.2.29)!
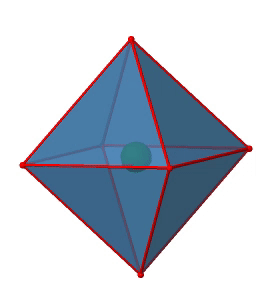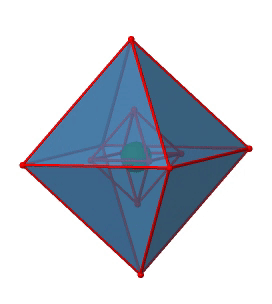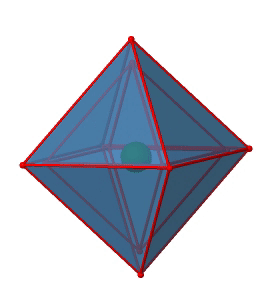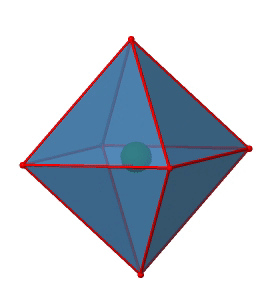
Figura 2.2.29 El centro de inversión del grupo de puntos octaédricos O h (Atribución: symotter.org/gallery)
Cada punto en el octaedreón se puede mover a través del centro de inversión hacia el otro lado, y el octaedro producido superpondrá al original. Siempre hay una operación de inversión asociada a un centro de inversión (Fig. 2.2.30).
A continuación, busquemos reflexiones de rotación. A continuación se puede ver una operación de rotación-reflexión S 6 (Fig. 2.2.31, izquierda).
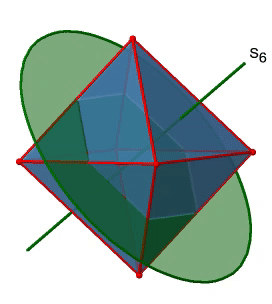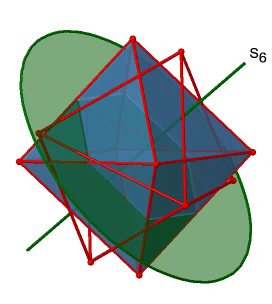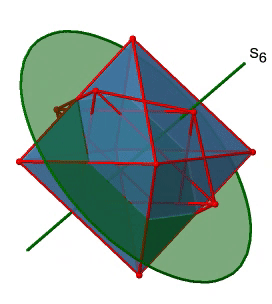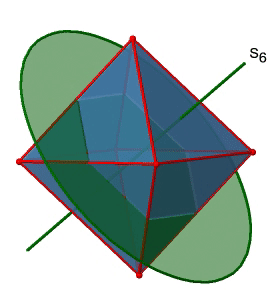
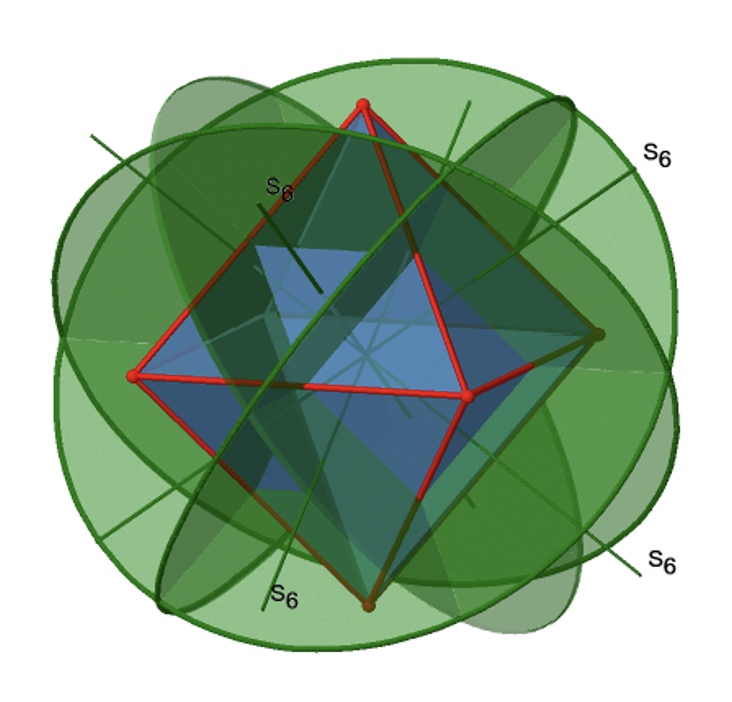
El eje S 6 incorrecto pasa a través de los centros de dos caras triangulares opuestas. Se puede ver que la rotación alrededor de 60° por sí sola no hace que el octaedro se superponga. Se requiere la reflexión en un plano perpendicular al eje impropio para lograr la superposición. En general, la rotación-reflexión intercambia la posición de las dos caras triangulares opuestas. ¿Cuántos ejes S 6 impropios hay? Dado que cada S 6 pasa por dos caras, y un octaedro tiene 8 caras debe haber 8/2=4 S 4 ejes. Se pueden ver todos ellos arriba (Fig. 2.2.31, derecha). Tenga en cuenta que están en la misma posición que los ejes 4C 3 que discutimos anteriormente. ¿Cuántas operaciones únicas están asociadas con ellas? Para un eje S 6 necesitamos considerar operaciones de S 6 1 a S 6 6. S 6 6 es lo mismo que la identidad por lo que no es única. El S 6 2 es lo mismo que un C 3 1 porque girar dos veces alrededor de 60° es lo mismo que girar alrededor de 120°, y reflejar dos veces es lo mismo que no reflejar en absoluto. De igual manera, un S 6 4 es lo mismo que un C 3 2. Girar cuatro veces por 60° es lo mismo que rotar dos veces por 120° y reflejar cuatro veces es lo mismo que no reflejar en absoluto. Además, un S 6 3 es lo mismo que una inversión. Después de tres rotaciones de 60° hemos girado 180°. Si reflexionamos después de eso, entonces esto es lo mismo que una operación S 2 1 que es lo mismo que una inversión. Por lo tanto, solo las operaciones S 6 1 y S 6 5 son únicas, todas las demás operaciones pueden expresarse mediante operaciones más simples (Fig. 2.2.32).
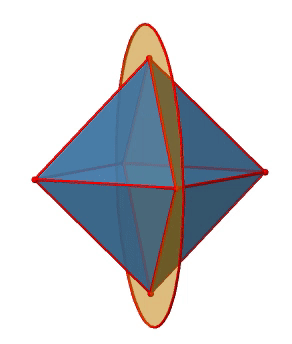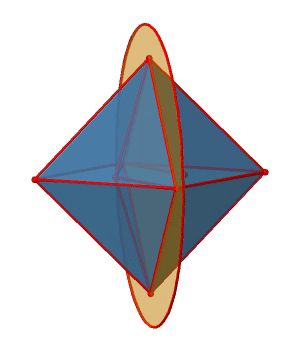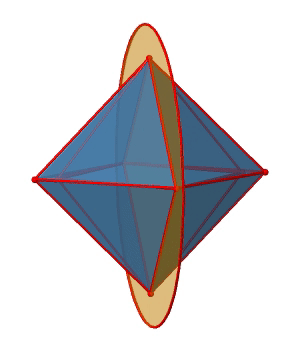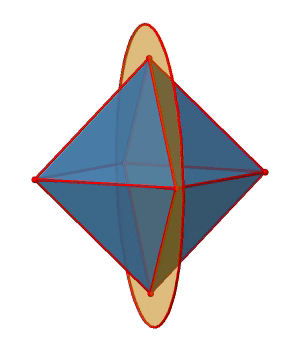
El octaedro también tiene S 4 ejes impropios, y se puede ver uno de ellos a continuación (Fig. 2.2.33, derecha).
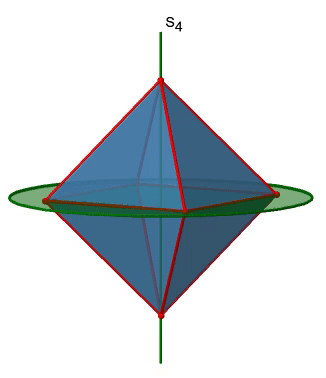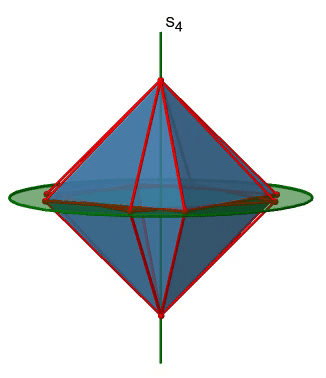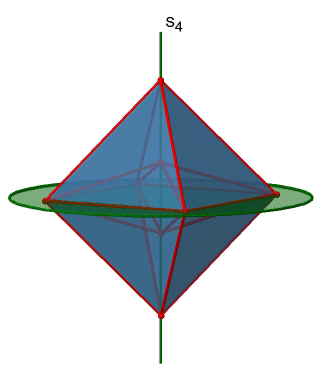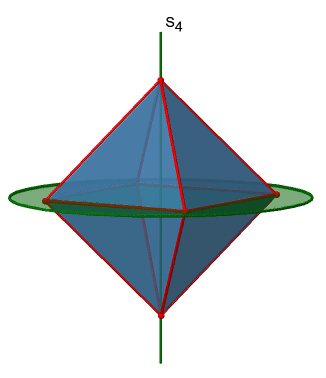
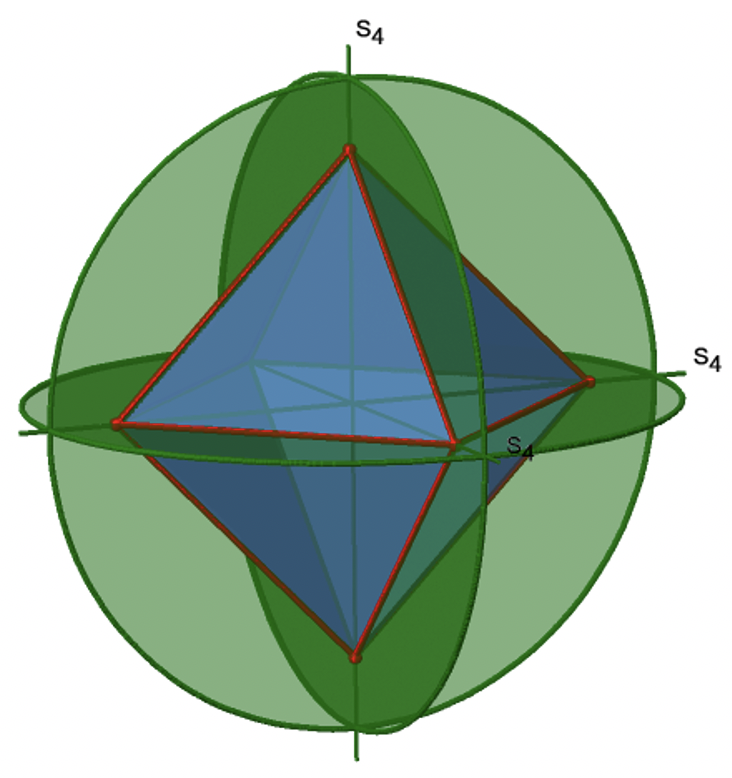
Pasa por dos esquinas opuestas del octaedro. El eje impropio S 4 aparentemente hace lo mismo que el eje C 4 que atraviesa los mismos dos vértices opuestos, pero en realidad no lo hace. Si bien rotar alrededor de 90° ya hace que el octaedro se superponga con su forma original, ejecutando la operación de reflexión después de que la rotación intercambie la posición de los dos vértices, y generalmente todos los puntos del octaedro por encima y por debajo del plano, respectivamente. En general, el S 4 mueve los puntos dentro del objeto de manera diferente en comparación con el C 4, lo que lo convierte en un elemento de simetría adicional y único. En general hay tres ejes S 4 impropios porque el octaedro tiene seis vértices y un S 4 pasa a través de dos vértices (Fig. 2.2.34).
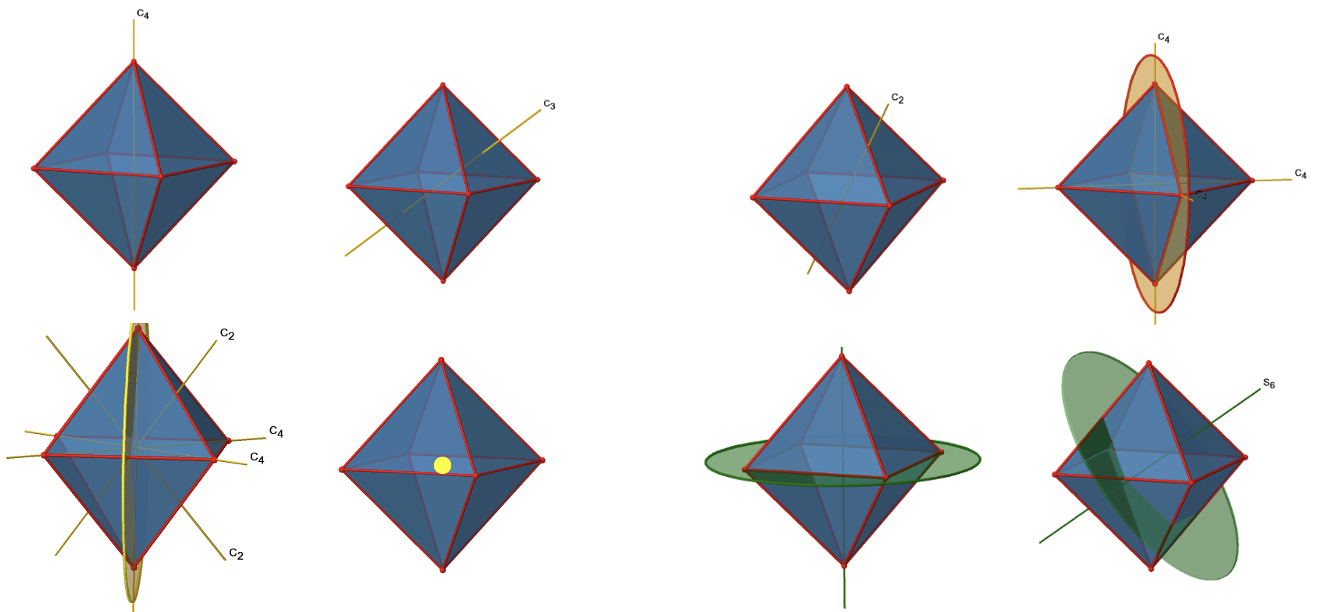
Aquí hay una visión general de todos los elementos y operaciones de simetría (Fig. 2.2.35 y 2.2.36). En general, ¡hay 48 operaciones únicas diferentes que uno puede realizar!
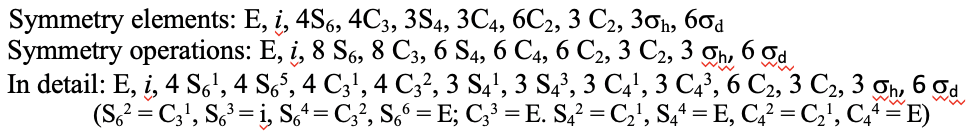
Al igual que el grupo de puntos T d, también el grupo de puntos O h tiene un subgrupo rotacional, denominado O. Tiene la identidad y las mismas rotaciones adecuadas que el grupo de puntos O h, pero no otras operaciones de simetría (Fig. 2.2.38). Un ejemplo es el núcleo del cúmulo de polioxometalato que se muestra a continuación (Fig. 2.2.37). Los polioxometalatos son aniones de racimo del grupo 5 y 6 elementos.
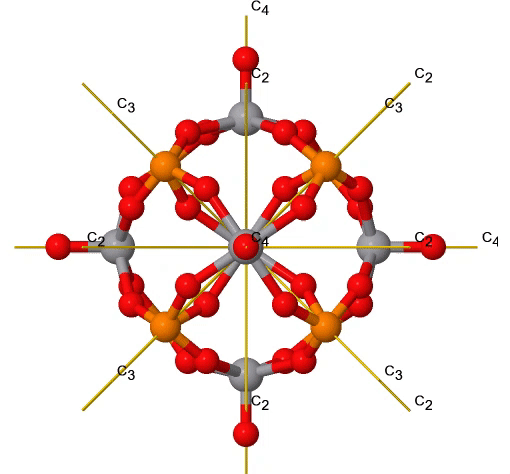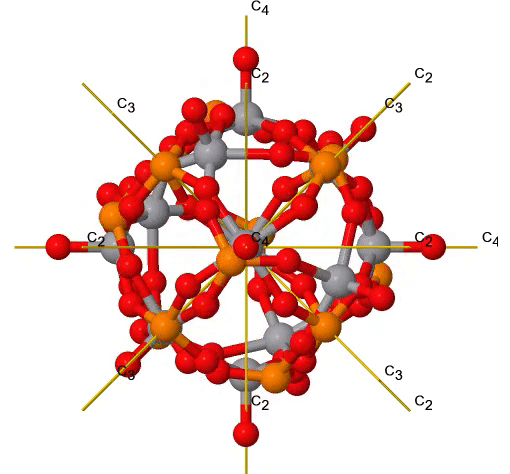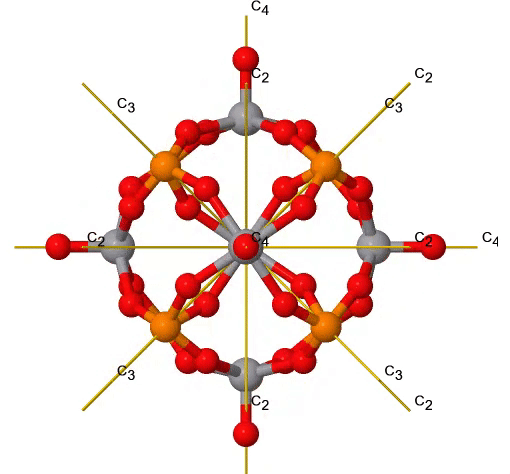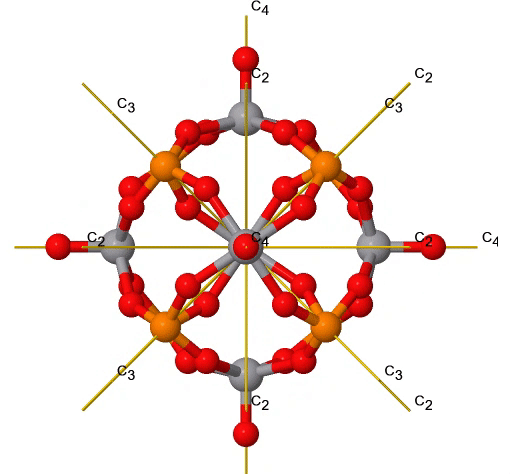
Figura 2.2.37 Rotaciones adecuadas en un núcleo de racimo de polioxometalato V 6 P 8 O 24. La rotación de C 3 está animada. (Atribución: symotter.org/gallery)
El grupo puntual O es generalmente raro.
Otro grupo de puntos de simetría alta es el grupo de puntos T h. También se puede derivar del grupo puntual O h. En este caso las operaciones S 4, C 4, C 2 ', y σ d se eliminan de la simetría octaédrica. Un ejemplo es el catión hexapiridil-hierro (2+) (Fig. 2.2.39).
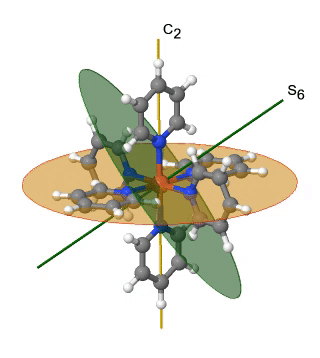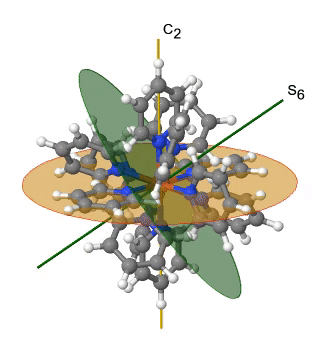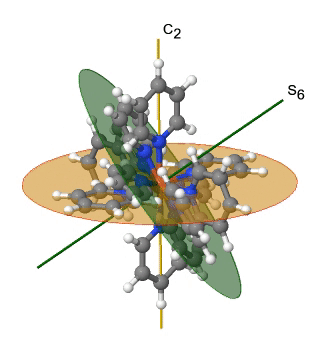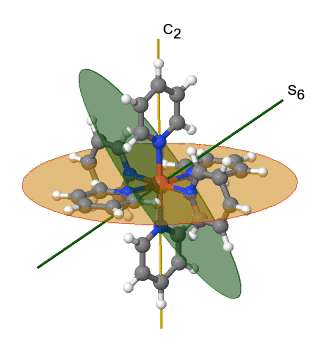
Figura 2.2.39 El catión hexapiridil hierro (2+) y sus elementos de simetría S 6 y C2. Se anima una operación S 6.
Se puede ver que los N-átomos de los ligandos de piridilo rodean octaédricamente a los átomos de Fe, pero la simetría se reduce de O h a T h debido a la forma plana de los ligandos piridilo. En particular la simetría C 4 se reduce a C 2. Esta reducción en la simetría conduce a la eliminación de los elementos de simetría S 4, C 2 'y σ d (Fig. 2.2.40).
El I h Grupo de Puntos
Los dos sólidos platónicos restantes, el icosaedro y el dodecaedro, pertenecen ambos al grupo puntual icosaédrico I h. Esto a pesar de que están hechos de diferentes polígonos (Fig. 2.2.41).
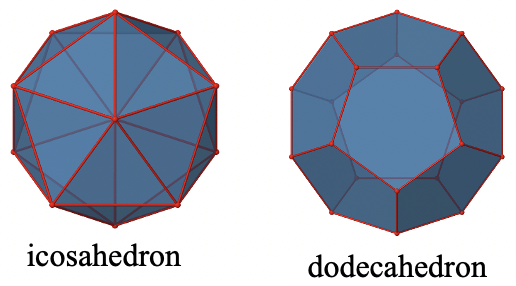
Debido a que pertenecen al mismo grupo de puntos, tienen exactamente las mismas operaciones de simetría. Un ejemplo para una molécula con forma icosaédrica es el anión molecular B 12 H 12 2-. Un ejemplo para una molécula con forma dodecaédrica es el dodecaedrano C 20 H 20.
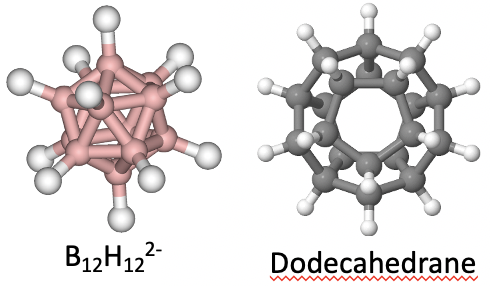
Determinemos los elementos de simetría y las operaciones de simetría para el ejemplo del icosaedro. También podríamos usar el dodecaedro, y los resultados serían los mismos. Los ejes principales del icosaedro son los ejes C 5. Se puede ver una de ellas, pasando por el centro del pnetagon compuesto por cinco caras triangulares abajo (Fig. 2.2.43).
Figura 2.2.43 Uno de los ejes C 5 del icosaedro se encuentra perpendicular al plano de papel que atraviesa el centro de un pentágono del icosaedro (Atribución: symotter.org/gallery)
Se puede entender que hay un C 5 al considerar que hay cinco caras triangulares haciendo un pentágono. El eje C 5 se asienta en el centro del pentágono. Podemos ver que cuando giramos alrededor de este eje C 5, entonces el icosaedro producido superpone al original. El eje C 5 atraviesa dos vértices opuestos del icosaedro. Debido a que un isosaedro tiene 12 vértices, debe haber seis ejes C 5 en general. Se pueden ver todos a continuación (Fig. 2.2.44).
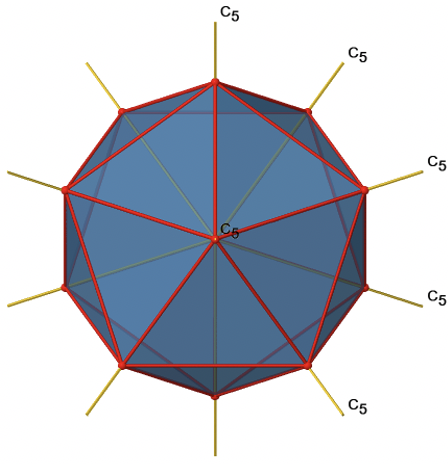
Hay cuatro operaciones de simetría únicas asociadas con un solo eje C 5, a saber, el C 5 1, el C 5 2, el C 5 3 y el C 5 4. El C 5 5 es lo mismo que la identidad. Debido a que hay seis ejes C 5, hay operaciones globales de simetría 6x4=24 C 5 (Fig. 2.2.45).
Además, hay ejes C 3. A continuación se muestra una de ellas, y se puede ver que pasa por los centros de dos caras triangulares opuestas (Fig. 2.2.46).
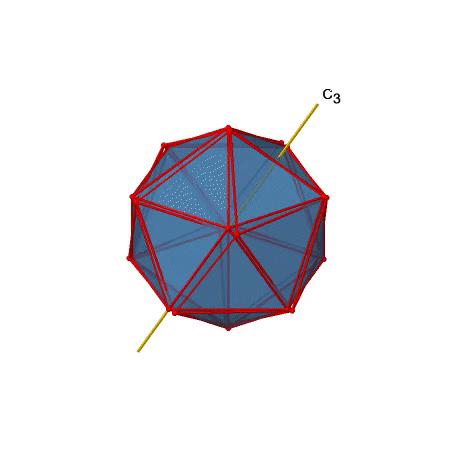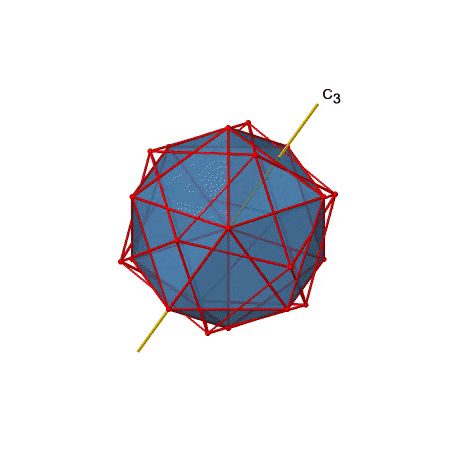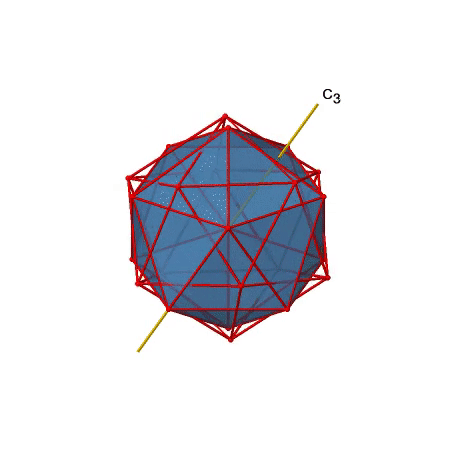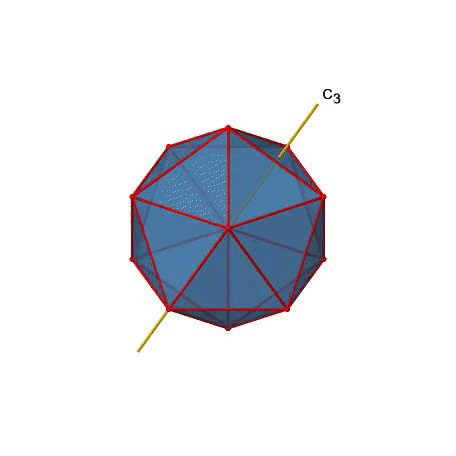
A medida que uno gira 120°, los átomos en las caras triangulares cambian su posición, y el icosaedro resultante se superpone al original. Como dice el nombre icosaedro, hay veinte caras en general.
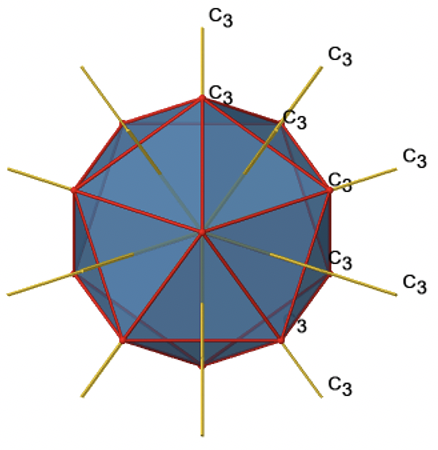
Debido a que un C 3 pasa a través de dos ejes opuestos, hay 20/2=10 ejes C 3 en general (Fig. 2.2.47). Cada eje C 3 está asociado con dos operaciones de simetría, a saber, C 3 1 y C 3 2. Por lo tanto, hay operaciones globales de simetría 10x2=20 C 3.
También hay ejes C 2 (Fig. 2.2.49). Pasan por los centros de dos bordes opuestos del icosaedro. Girando alrededor del eje C 2 mostrado hace que el icosaedro se superponga.
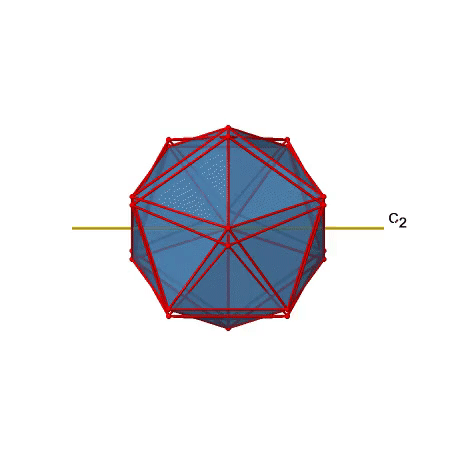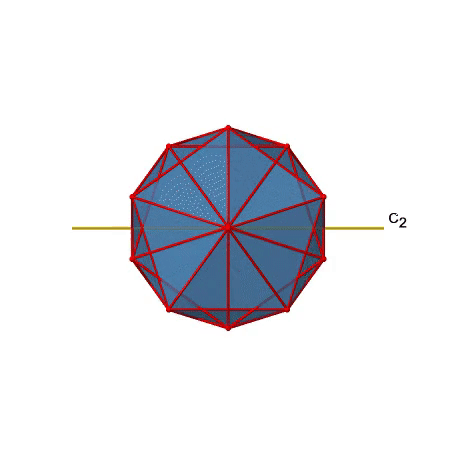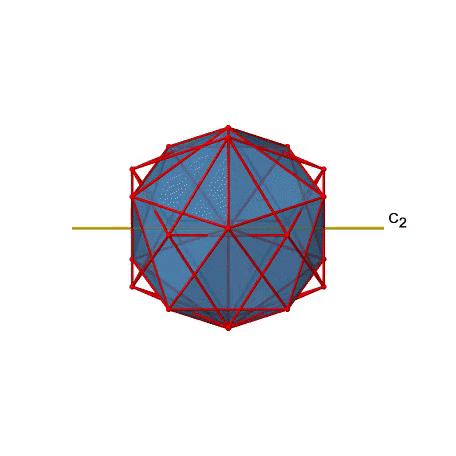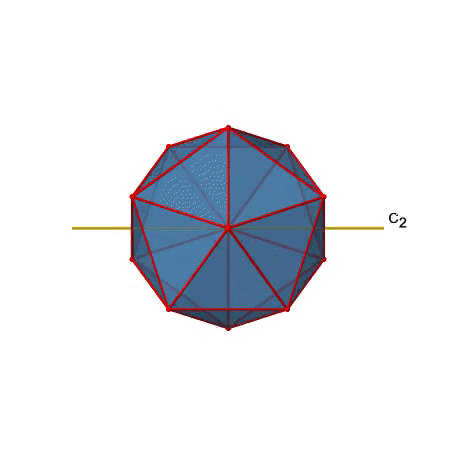
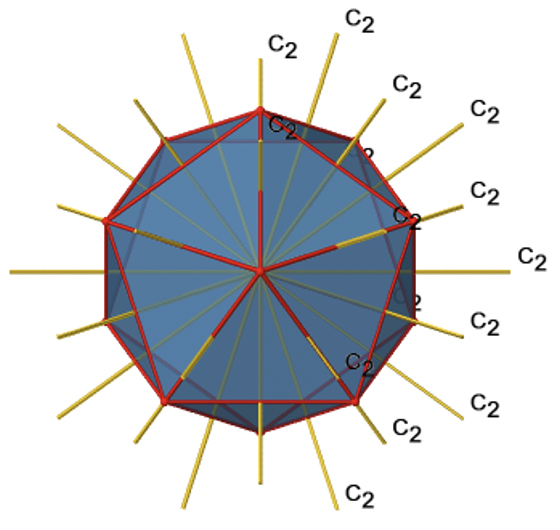
Un isosaedro tiene en general 30 bordes. Debido a que un eje C 2 pasa por los centros de dos bordes opuestos, podemos entender que hay 30/2=15 ejes C 2. Hay una operación única de C 2 por eje, y por lo tanto hay 15 operaciones C 2 (Fig. 2.2.50).
Ahora hemos encontrado todas las rotaciones adecuadas. Busquemos planos espejo, siguiente. Se puede ver un plano espejo a continuación (Fig. 2.2.51).
Figura 2.2.51 Un plano espejo en el grupo de puntos icosaédricos (Atribución: symotter.org/gallery)
Contiene dos bordes opuestos. También bisecta otros dos bordes. Un icosaedro tiene en general 30 bordes, por lo tanto hay 30/2=15 planos de espejo. Se pueden ver todos a continuación (Fig. 2.2.52 y Fig. 2.2.53)).
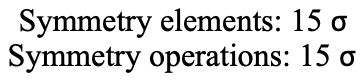
El icosaedro también tiene un centro de inversión en el centro del icosaedro (Fig. 2.2.54 y Fig. 2.2.55)).
Figura 2.2.54 El centro de inversión en el icosaedro (Atribución: symotter.org/gallery)
A medida que llevamos a cabo la operación asociada, una simetría, todos los puntos del isosaedro se mueven a través del centro de inversión hacia el otro lado.
Busquemos ahora rotaciones inadecuadas. Los ejes rotacionales inadecuados con el orden más alto son S 10 ejes. Se ubican en la misma posición que los ejes C 5, y pasan por dos esquinas opuestas (Fig. 2.2.56).
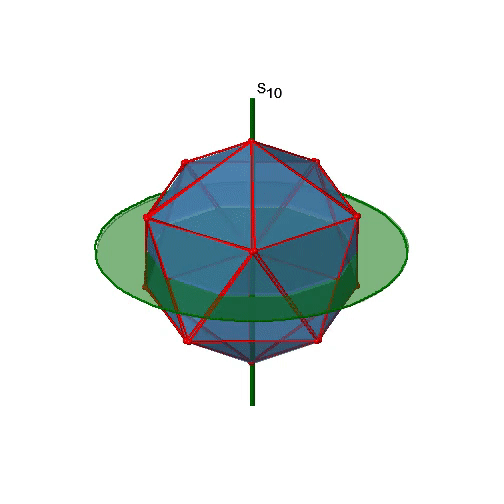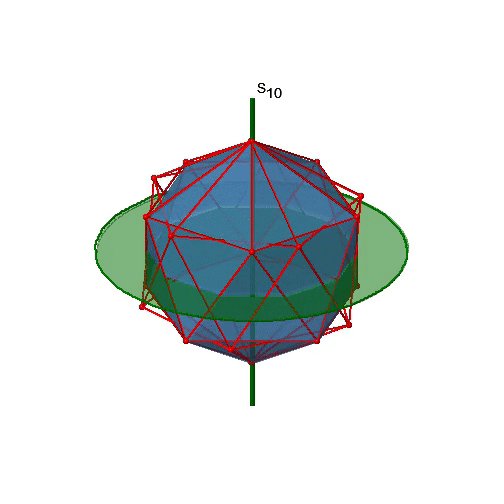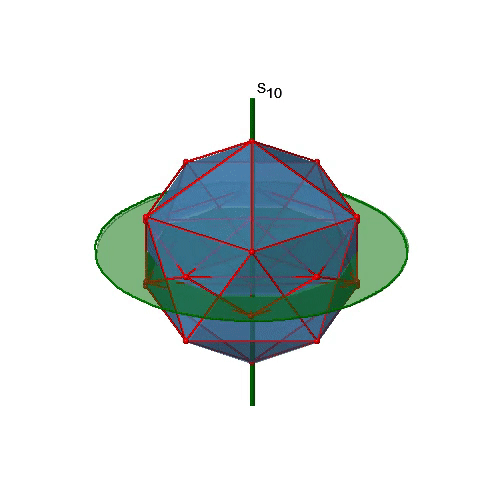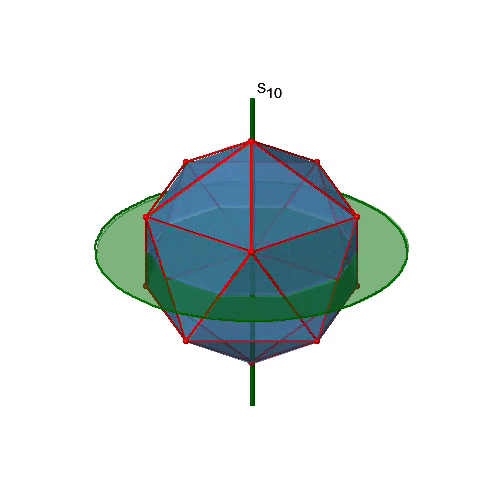
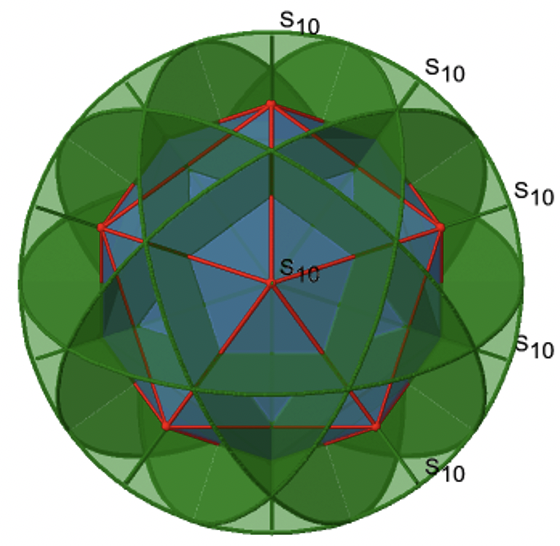
El S 10 existe porque en un icosaedro hay pares de pentágonos coplanares que están orientados escalonados uno respecto al otro. La rotación alrededor de 36° lleva a un pentágono en posición eclipsada con relación al otro, pero la superposición solo se logra después de la reflexión en el plano especular perpendicular al eje de rotación. Debido a que un S 10 pasa por dos vértices opuestos, y hay 12 vértices hay 6 S 10 ejes impropios. Para cada eje hay cuatro operaciones de simetría únicas, la S 10 1, la S 10 3, la S 10 7 y la S 10 9. Por lo tanto, existen en general 4x6=24 operaciones posibles (Fig. 2.2.57).
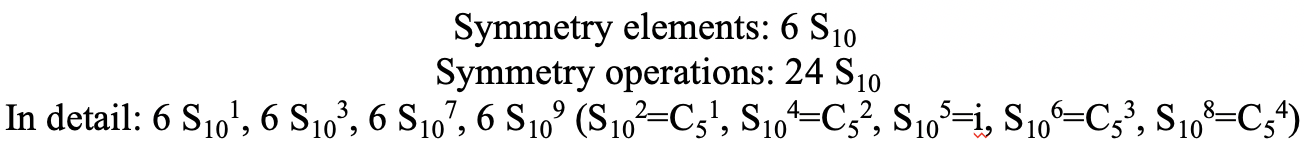
¿Los ejes rotacionales de orden inferior son inadecuados? Sí, hay ejes S 6 que pasan por los centros de dos caras triangulares opuestas (Fig. 2.2.58). Este elemento de simetría existe porque las dos caras triangulares están en orientación escalonada entre sí. La rotación por sí sola trae una cara en orientación eclipsada con relación a la otra, pero se requiere reflexión en un plano espejo perpendicular al eje para lograr la superposición. Los ejes S 6 están en la misma ubicación que los ejes C 3.
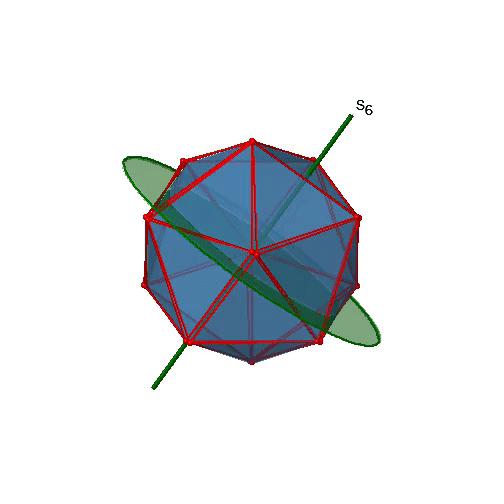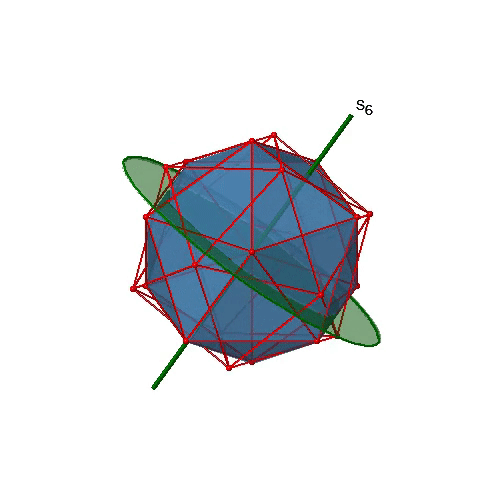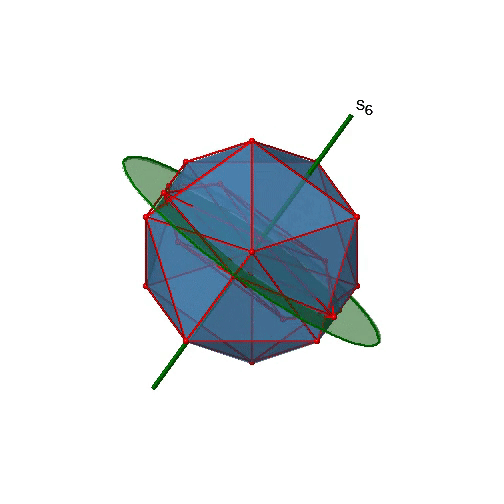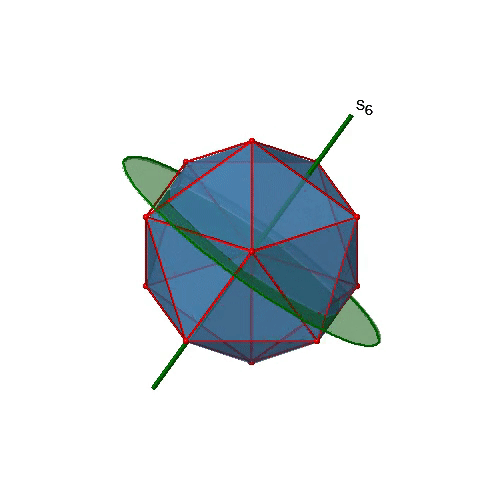
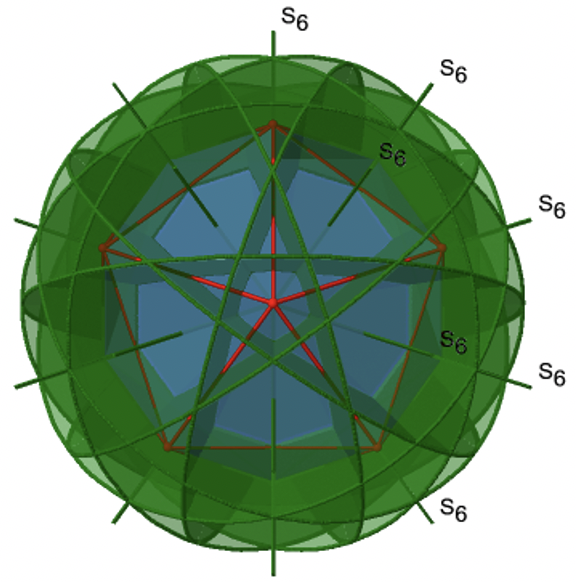
Hay 10 ejes S 6 porque hay veinte caras y un eje pasa a través de dos caras opuestas. Solo las operaciones S 6 1 y S 6 5 son operaciones únicas S 6, todas las demás pueden expresarse mediante operaciones más simples. Por lo tanto hay en general 10 S 6 1 +10 S 6 5 = 20 S 6 operaciones (Fig. 2.2.59).
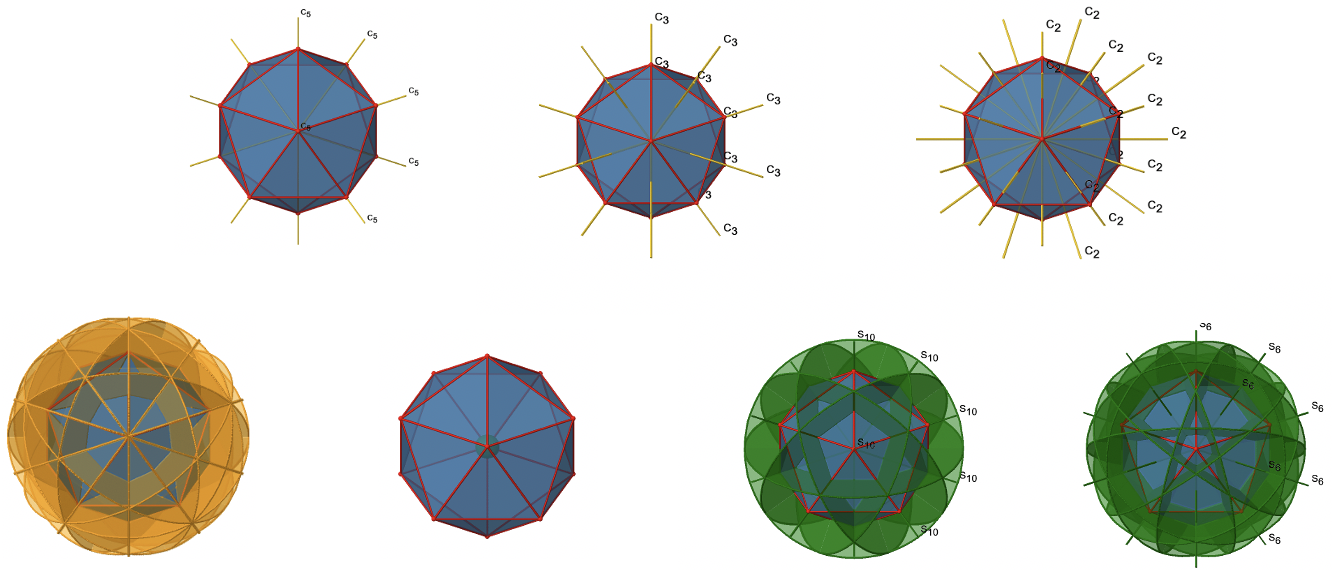
Ahora hemos encontrado todas las operaciones de simetría para la simetría I h. En general hay 120 operaciones haciendo del grupo puntual I h el grupo puntual con la simetría más alta (Fig. 2.2.60 y Fig. 2.2.61).
También el grupo puntual I h tiene un subgrupo rotacional.
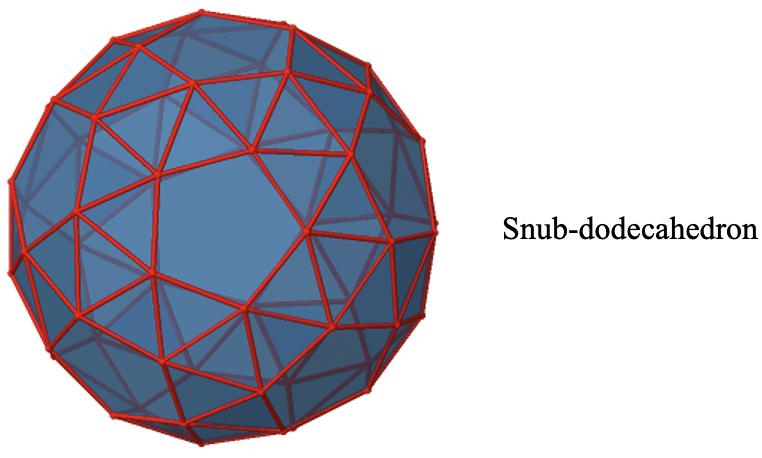
Se llama I. Un ejemplo de un objeto con esta simetría es el snub-dodecaedro (Fig. 2.2.62). Tiene la identidad, y todas las operaciones de rotación adecuadas del grupo puntual O h, pero se eliminan la inversión, las reflexiones de rotación y los planos especulares (Fig. 2.2.63).
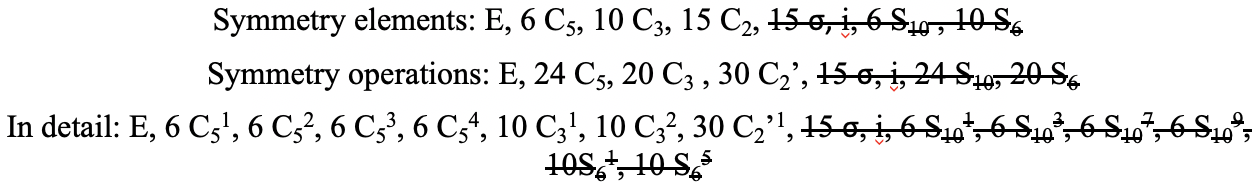
Grupos de puntos cíclicos
Después de haber discutido los grupos de puntos de simetría alta y baja, veamos a continuación los grupos de puntos cíclicos. Tienen la propiedad de que solo tienen un solo eje de rotación n-fold apropiado, pero no otros ejes adecuados. En el caso más sencillo no cuentan con ningún elemento de simetría adicional como planos de espejo o reflejos de rotación. Estos grupos de puntos se denotan C n donde n es el orden del eje apropiado. Un ejemplo es la molécula de peróxido de hidrógeno H 2 O 2 (Fig. 2.2.64).
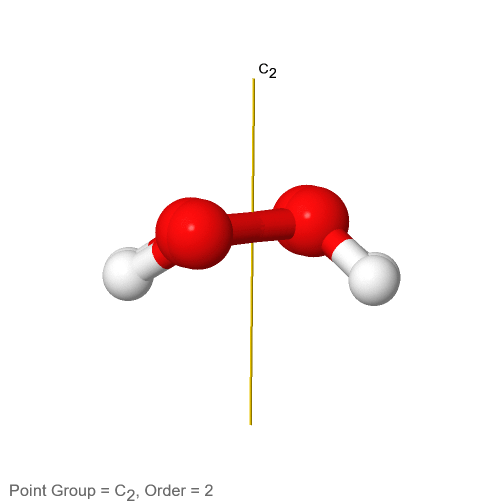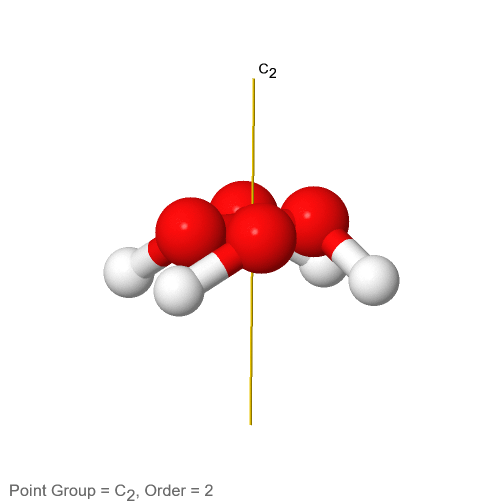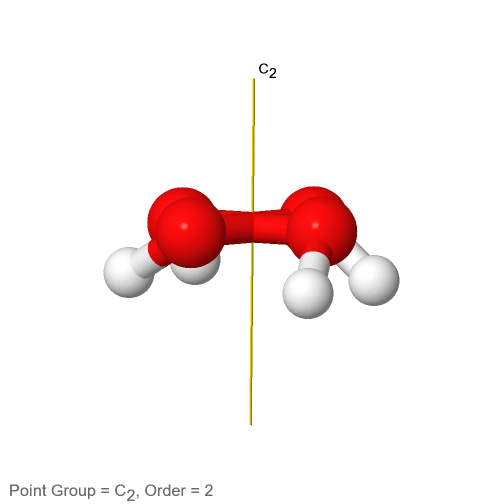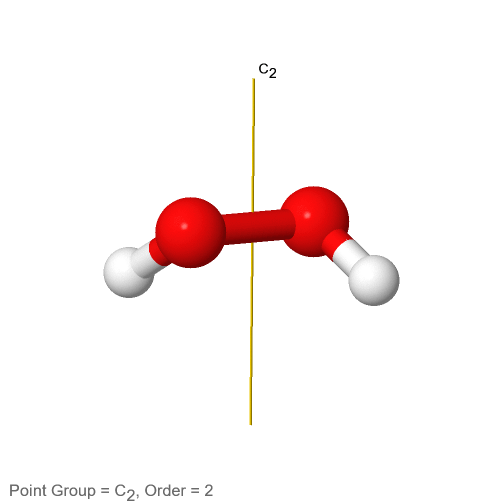
Figura 2.2.64 El eje de rotación C2 del peróxido de hidrógeno
Tiene una denominada estructura de techo debido a su no planaridad. Un átomo de hidrógeno apunta hacia nosotros, y el otro apunta lejos de nosotros. Esta estructura se debe a los dos pares electrón-solitario en cada átomo de oxígeno hibridado sp 3. Estos pares electrón-solitario consumen algo más espacio que los átomos de H, y hay repulsión electrostática entre los pares de electrones solitarios. Por lo tanto, los pares solitarios de electrones en los diferentes átomos de oxígeno intentan lograr la mayor distancia entre sí. Esto obliga a los átomos de H a salir del plano, lo que lleva a la estructura del techo del peróxido de hidrógeno. Debido a que la molécula H 2 O 2 no es plana, solo tiene un único eje C 2, pero ningún otro elemento de simetría además de la identidad. El eje C 2 pasa por el centro del enlace O-O. La ejecución de la operación C 2 intercambia tanto los átomos O como los átomos H.
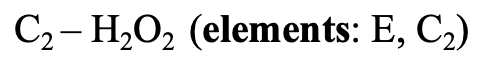
Definición: Grupos cíclicos C n
Los grupos cíclicos tienen un grupo axipiramidal rotacional
Otra clase de grupos son los grupos piramidales, denotados C nv. Cuentan con n planos especulares verticales que contienen el eje principal C n además del eje principal C n. Generalmente las moléculas pertenecientes a grupos piramidales se derivan de una pirámide n-gonal. Una pirámide n-gonal tiene un polígono n-gonal como base que está tapado (Fig. 2.2.66).
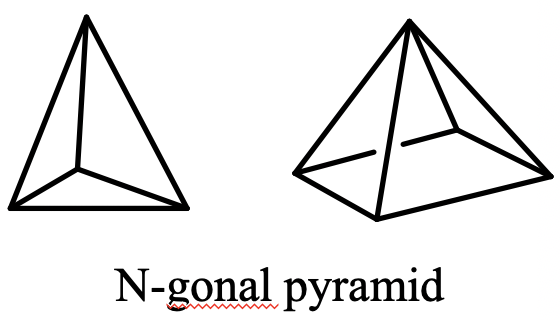
Por ejemplo, una pirámide trigonal tiene una base triangular que está tapada, una pirámide tetragonal tiene un cuadrado que está tapado, y así sucesivamente. El eje apropiado asociado a una pirámide específica tiene el orden n y pasa por la punta de la pirámide y el centro del polígono. Un ejemplo de una molécula con forma piramidal trigonal es el NH 3 (Fig. 2.2.67).
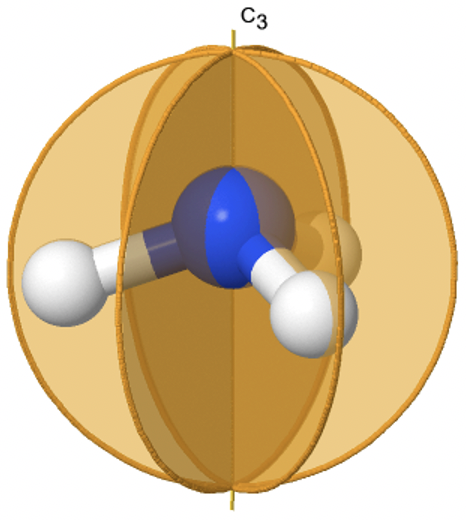
Los tres átomos de H forman la base triangular de la pirámide, que está cubierta por el átomo de N. La molécula NH 3 pertenece al grupo puntual C 3v. El eje C 3 va a través del átomo de N que es la punta de la pirámide, y el centro del triángulo definido por los átomos de H. Hay tres planos de espejo verticales que contienen el eje C 3. Cada uno de ellos pasa por un enlace N-H (Fig. 2.2.68).
Definición: Grupos piramidales C nv
Los grupos piramidales tienen n plano (s) vertical (s) además del eje principal C n.
El Grupo Lineal C ∞ v
Un polígono n-gonal especial es el cono. Un cono puede concebirse como una pirámide n-gonal con un número infinito n de esquinas en la base (Fig. 2.2.69).
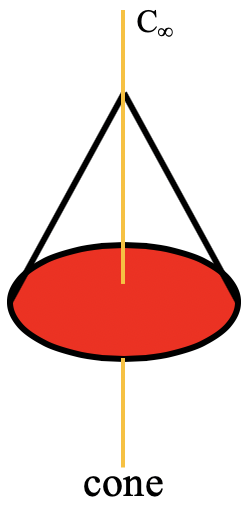
En este caso el orden del eje de rotación que pasa por la punta del cono y el centro de la base circular es infinito. Esto también significa que hay un número infinito de planos especulares verticales que contienen el eje C ∞ (Fig. 2.2.71). El grupo de puntos que describe la simetría de un cono se denomina grupo de puntos lineales C ∞ v. Moléculas polares lineales como CO, HF, N 2 O y HCN pertenecen a este grupo puntual. Se puede ver la molécula HCN con su eje C ∞ y su número infinito de planos especulares verticales a continuación (Fig. 2.2.70).
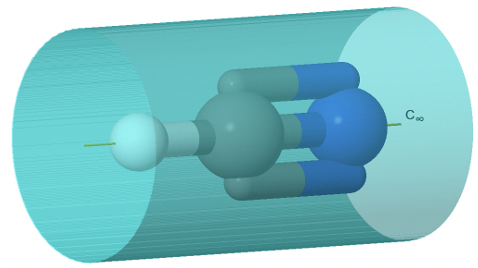
El número infinito de planos especulares, mostrados en azul, están formando un cilindro que rodea a la molécula.
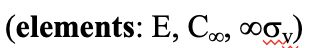
Definición: Grupo lineal C oov
El grupo lineal C ∞ v tiene un número infinito de planos de espejo verticales que contienen un eje C ∞
Grupos de Reflexión
Si agregamos un plano de espejo horizontal en lugar de n planos de espejo verticales a un eje rotacional apropiado C n llegamos a un grupo de puntos de reflexión tipo C nh. La presencia de los planos especulares horizontales también genera un eje impropio del orden n. Esto se debe a que cuando se puede girar y reflejar perpendicularmente a los ejes rotacionales de manera independiente, entonces también debe ser posible hacerlo en combinación. Un ejemplo de una molécula que pertenece a un grupo de reflexión es el trans-difluorodiazeno N 2 F 2 (Fig. 2.2.72).
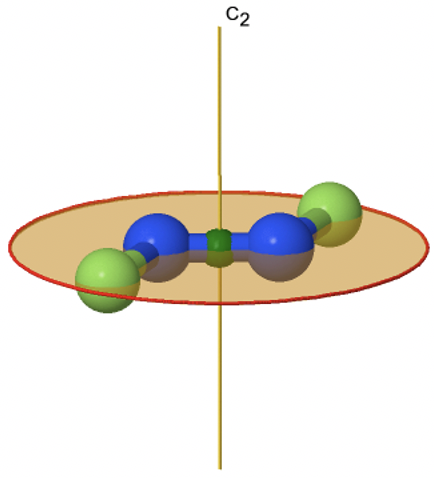
Se trata de una molécula plana con un eje C 2 que atraviesa la mitad del doble enlace N-N, y de pie perpendicular al plano de la molécula. El plano espejo horizontal se encuentra perpendicular al eje C 2, y está dentro del plano de la molécula. Hay un centro de inversión adicional porque debe existir un S 2 que es lo mismo que un centro de inversión. El centro de inversión se encuentra en el medio de los enlaces N-N. En general, la molécula tiene la simetría C 2h.
Definición: Grupo de Reflexión C nh
Un grupo de reflexión tiene un plano horizontal perpendicular al eje principal Cn
Grupos Diedros
Los grupos diedros son grupos de puntos que tienen n ejes C 2 adicionales que se encuentran perpendiculares al eje principal del orden n. Si no hay otros elementos de simetría, entonces el grupo de puntos es del tipo D n.
3_C3.gif)
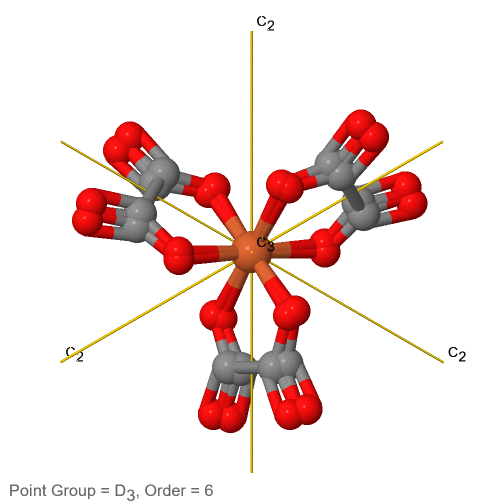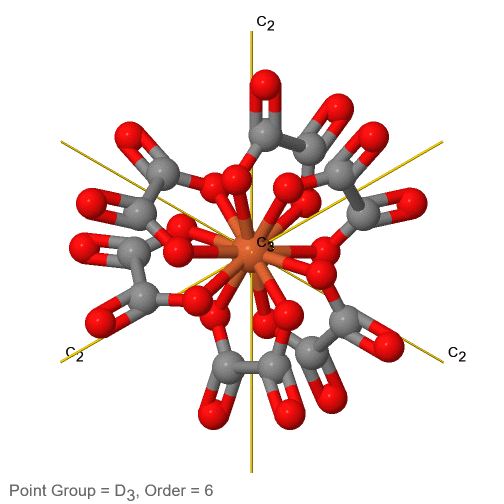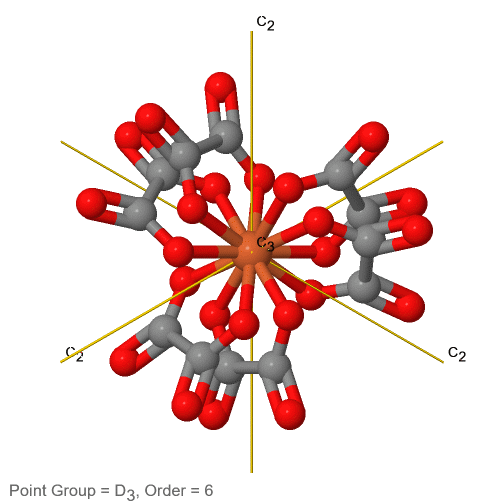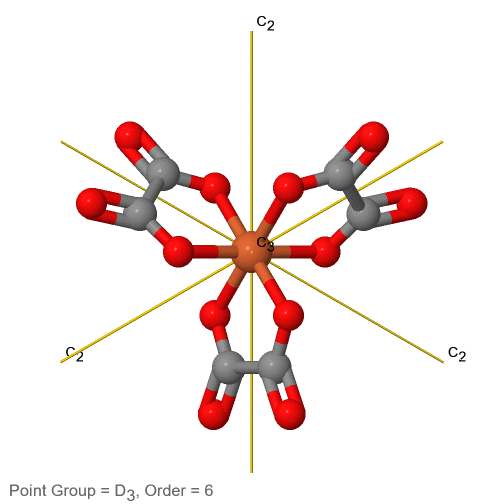
Figura 2.2.74 El ion tris-oxolato ferrato (3-) y sus elementos de simetría
Por ejemplo en el grupo de puntos D 3 hay un eje principal C 3, y tres ejes C 2 adicionales, pero ningún otro elemento de simetría (Fig. 2.2.75). El ion tris-oxolato ferrato (3-) pertenece a este grupo puntual (Fig. 2.2.75). Se puede ver que el eje C 3 se encuentra perpendicular al plano de papel, y hay tres ejes C 2 en el plano de papel.
Definición: Grupos Diedros D n
En un grupo de puntos del tipo D n hay un eje principal de orden n, n C 2 ejes, pero no hay otros elementos de simetría.
Si se agrega un plano espejo horizontal al eje C n y a los ejes n C 2 llegamos a los grupos de puntos prismáticos D nh (Fig. 2.2.76). La adición del plano de espejo horizontal genera más elementos de simetría, a saber, un S n y n planos de espejo vertical.
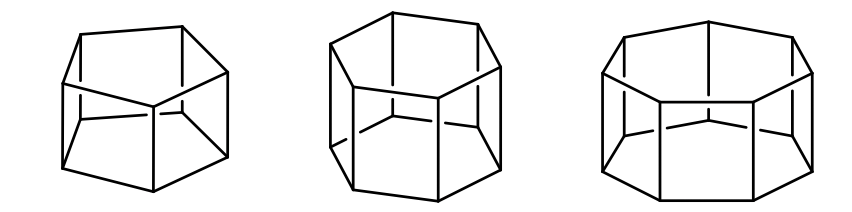
Generalmente, las moléculas pertenecientes a este grupo puntual derivan de prismas n-gonales. El orden del eje principal es el mismo que el número de esquinas de los polígonos del que está hecho el prisma.
Definición: Grupos Prismáticos D nh
En los grupos de puntos prismáticos hay un plano espejo horizontal perpendicular al eje principal C n. También hay n C 2 ejes.
Un ejemplo para una molécula perteneciente a un grupo puntual prismático es PF 5 (Fig. 2.2.77).
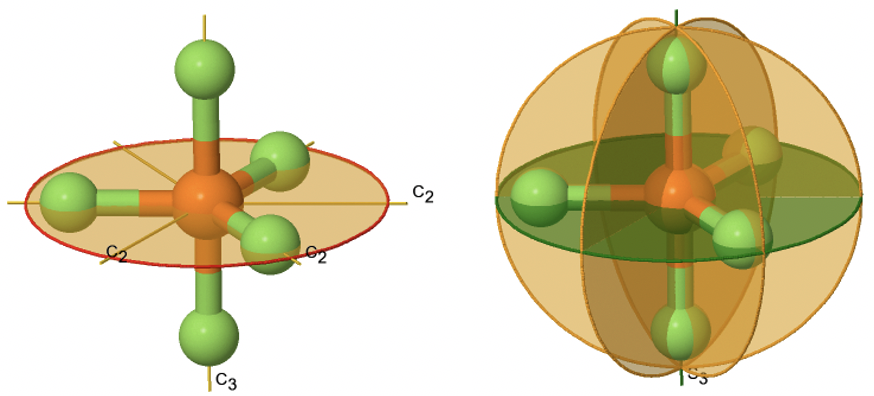
Tiene una forma bipiramidal trigonal. El eje C 3 atraviesa los átomos F axiales de la molécula, y los tres ejes C 2 pasan por los tres átomos F ecuatoriales. El plano espejo horizontal se encuentra perpendicular al eje C 3 principal y se ubica dentro del plano ecuatorial de la molécula. Además, están los planos especulares verticales que contienen el eje C 3, y pasan por los tres enlaces P-F ecuatoriales. También hay un eje S 3 que superpone al eje C 3. En suma:
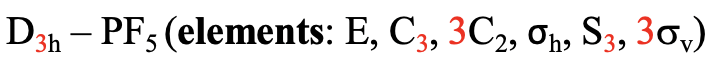
Un caso especial de un grupo D nh es el grupo lineal D ∞ h. Un objeto que tiene esta simetría es un cilindro. Un cilindro puede concebirse como un prisma con un número infinito de vértices. Así, el eje principal que pasa por un cilindro tiene orden infinito. Debido al orden infinito del eje principal, existe un número infinito de ejes C 2 que se encuentran perpendiculares al eje principal. Se puede ver uno de esos C 2 pasando por el cilindro (Fig. 2.2.79).
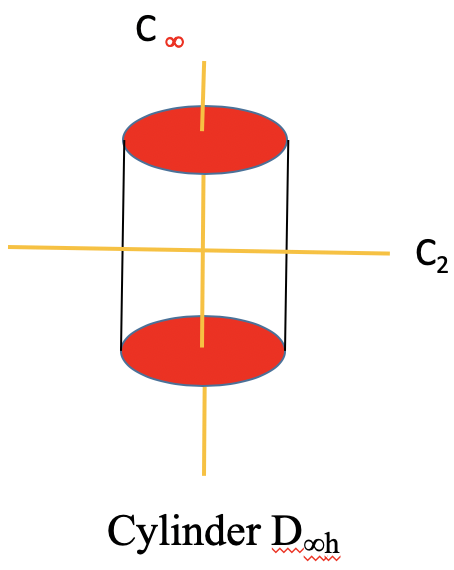
Ahora también hay un eje impropio de orden infinito, así como un número infinito de planos especulares verticales. Las moléculas lineales no polares como H 2, CO 2 y acetileno C 2 H 2 pertenecen al grupo puntual D ∞ h. Se puede ver el eje C ∞ pasando a través de una molécula de CO 2 a continuación (Fig. 2.2.80).
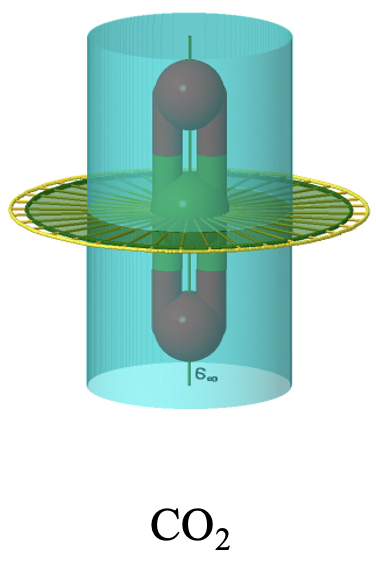
Se puede ver el número infinito de planos de espejo verticales como un cilindro azul. El número infinito de ejes C 2 se muestra unas líneas amarillas que van alrededor de la molécula. En suma:
Definición: Grupo lineal D ooh
En el grupo de puntos D ∞ h hay un número infinito de n C 2 ejes además del eje principal de orden infinito, un número infinito de planos especulares verticales y un plano espejo horizontal.
Si agregamos n planos de espejo verticales al eje principal y a los ejes n C 2, llegamos al grupo de puntos D nd. Los planos de espejo vertical son planos de espejo diedro porque bisectan el ángulo entre los ejes C 2. Un ejemplo es la molécula de etano en conformación escalonada que tiene la simetría D 3d (Fig. 2.2.82).
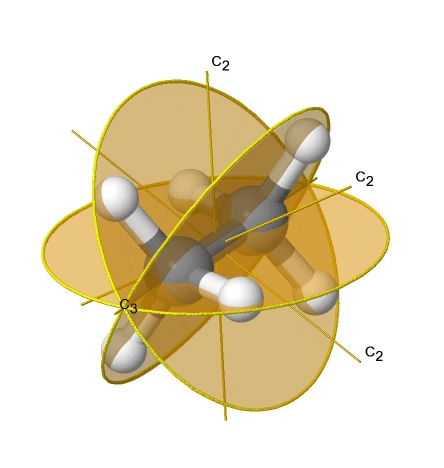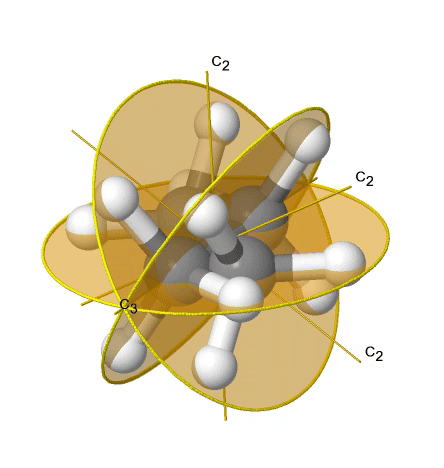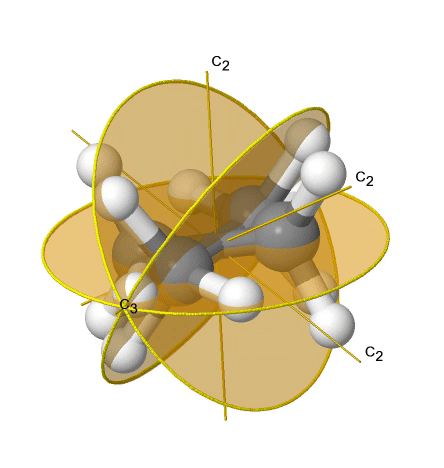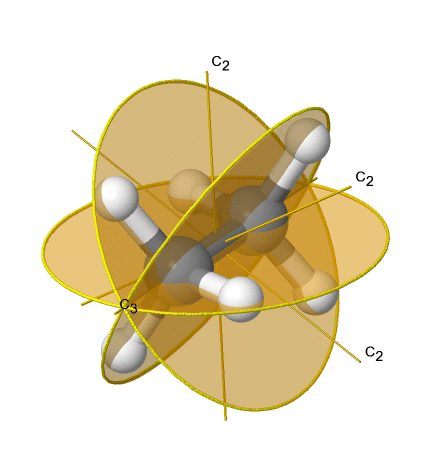
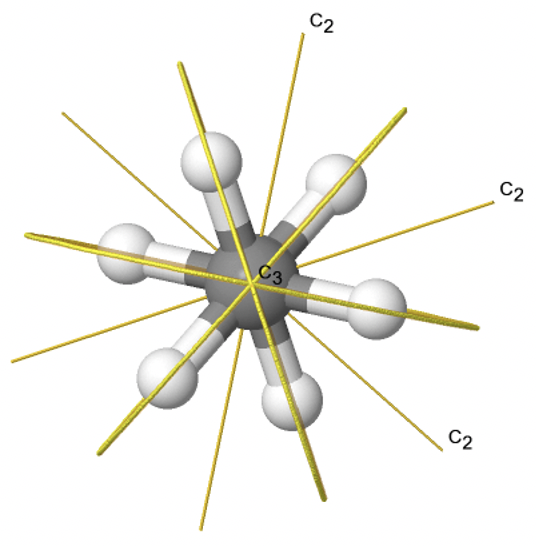
El eje C 3 va a lo largo del enlace C-C, y los ejes 3C 2 pasan por la mitad del enlace carbono-carbono, y bisecan el ángulo entre dos hidrógenos y un átomo de carbono. Los tres planos de espejo diedro pasan a través de los enlaces C-H. Además, la molécula de etano tiene un eje S 6, y un centro de inversión. En suma:
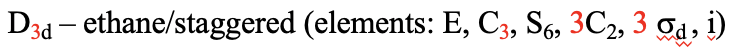
Definición: D nd
En este tipo de grupo de puntos hay n planos de espejo diedro que contienen el C n y bisecan el ángulo entre ejes C 2 adyacentes
Grupos de puntos rotacionales inadecuados
La última clase de grupos de puntos a discutir son los grupos de puntos de rotación inadecuados. Los únicos tienen un eje rotacional apropiado, y un eje rotacional incorrecto que tiene el doble del orden del eje de rotación adecuado (Fig. 2.2.85). Puede haber un centro de inversión presente dependiendo del orden de los ejes adecuados e impropios. Un ejemplo la molécula de tetrametilcicloocta-tetraeno (Fig. 2.2.84).
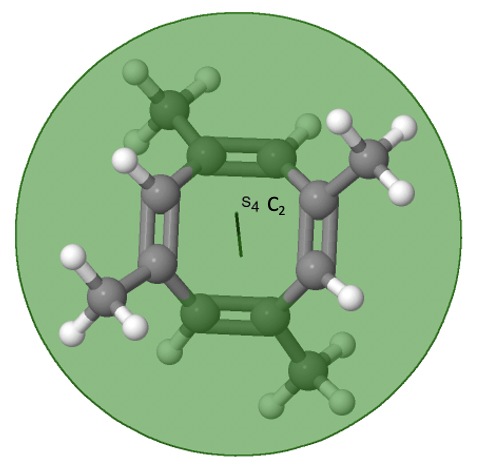
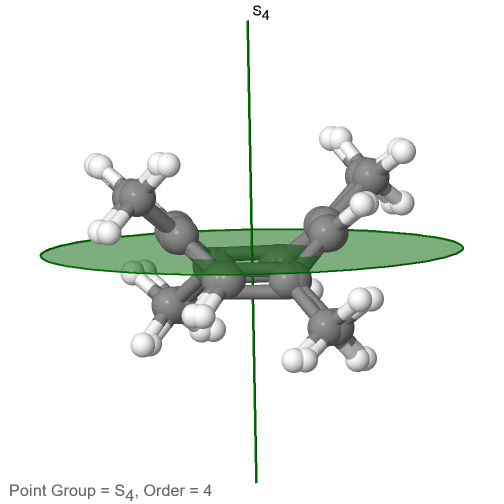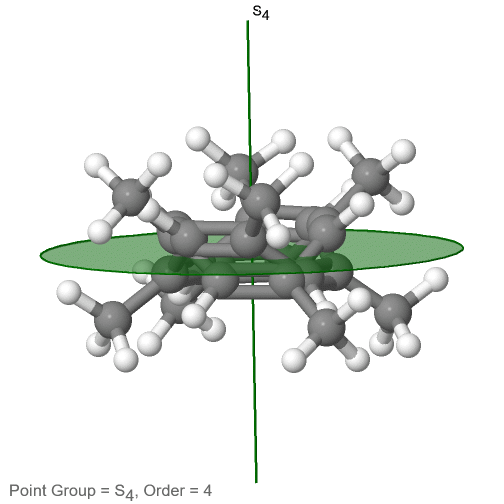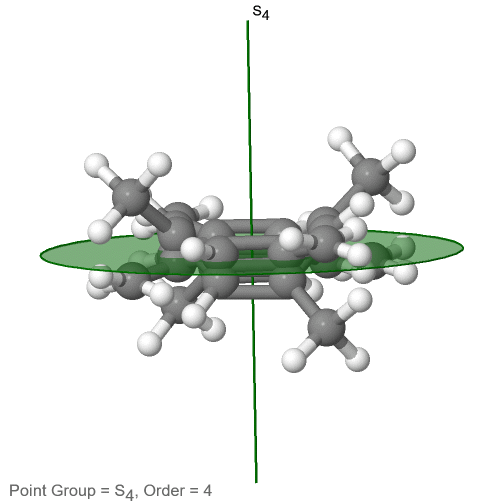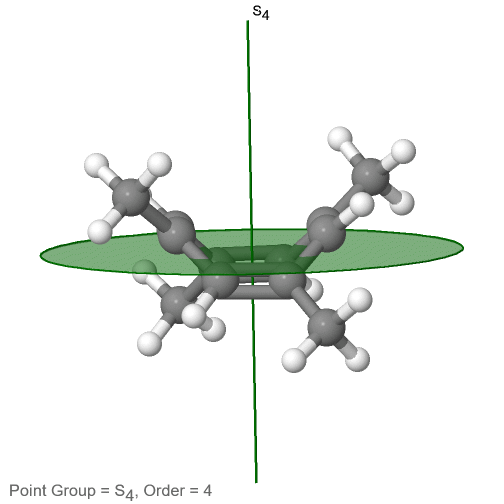
Figura 2.2.84 Los ejes S 4 y C 2 de tetrametilcicloocta-tetraeno
Tiene un eje S 4 y un C 2 como los únicos elementos de simetría además de la identidad. Girar 90° solo no superpone la molécula porque dos dobles enlaces C-C se encuentran por encima del plano y dos por debajo del plano. Además, dos grupos metilo opuestos se encuentran por encima y por debajo del plano respectivamente. Por lo tanto, necesita la reflexión adicional para lograr la superposición. También hay un eje C 2 que se encuentra en las mismas ubicaciones que el eje S 4.
Guía para la Determinación de Grupos de Puntos
Con los conocimientos que tienes, puedes identificar inequívocamente el grupo puntual de una molécula. La clave del éxito es que se puedan ver los elementos de simetría en la molécula. Esto requiere práctica. Con suficiente práctica se puede identificar el grupo puntual de una molécula de inmediato. Hasta, puedes usar guías, que puedes seguir para identificar un grupo de puntos. Dicha guía hace preguntas sistemáticas sobre la presencia o ausencia de un elemento de simetría. Dependiendo de si respondes la pregunta con sí o no puedes seguir la guía en una dirección particular. Eventualmente, después de haber respondido suficientes preguntas el guía te llevará al grupo de puntos respectivo. Puede ver un gráfico de este tipo a continuación (Fig. 2.2.86).
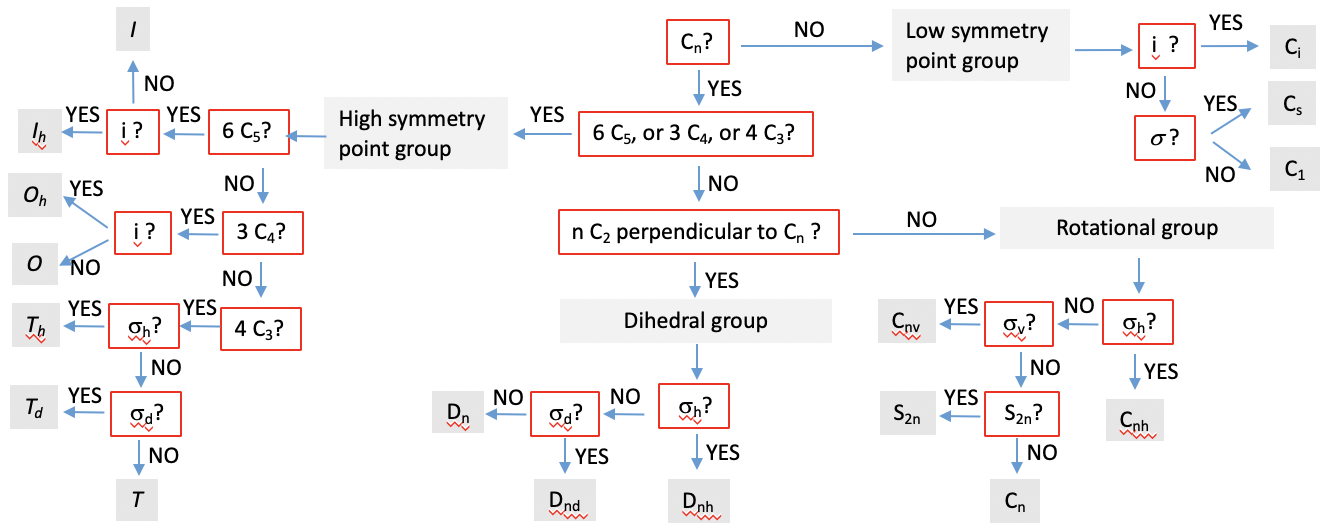
Primero puedes preguntar si hay al menos un C n presente. Si no, entonces la molécula debe estar en un grupo de puntos de simetría baja. Si hay un centro de inversión, el grupo de puntos es C i. Si no podemos preguntar a continuación, si hay un plano espejo. En caso afirmativo es C s, y si no el grupo de puntos es C 1. Si se puede descartar un grupo de puntos de simetría baja, entonces podemos preguntar a continuación, si hay un grupo de puntos de simetría alta. Este es el caso cuando existen ejes rotacionales 4C 3, 3C 4 o 6C 5 presentes, lo que representa simetría tetraédrica, octaédrica e icosaédrica, respectivamente. Si hay un centro de inversión en caso de que esté presente un C 5, el grupo de puntos es I h. Si no, es I. De igual manera, si hay 3C 4 ejes, y un centro de inversión, el grupo de puntos debe ser O h. Si no hay centro de inversión el grupo de puntos es O. Si hay 4C 3 ejes, el grupo de puntos debe ser de tipo T. Si además hay un plano de espejo horizontal, entonces el grupo de puntos debe ser T h. Si no, podemos preguntar siguiente es que hay planos de espejo diedro. En caso afirmativo, el grupo de puntos es T d, de lo contrario es T. Ahora hemos comprobado todos los grupos de puntos de simetría alta.
Si se pueden descartar grupos de puntos de alta simetría, preguntamos si hay n C 2 ejes además del eje principal C n. Si esto es así, entonces debemos tener un grupo diedro del tipo D. A continuación preguntamos, si hay un plano espejo horizontal. En caso afirmativo, el grupo de puntos debe ser D nh. Si no, preguntamos si hay planos de espejo diedro. En caso afirmativo, el grupo de puntos es D nd. Si no hay planos espejo en absoluto, entonces el grupo de puntos es D n. Si no hay n C 2 ejes además del C n, el grupo debe ser ya sea un grupo rotacional o un grupo de rotación impropio. A continuación preguntamos, si hay un plano espejo horizontal. En caso afirmativo, entonces el grupo de puntos es del tipo C nh. Si no, preguntamos si hay planos de espejo verticales. En caso afirmativo, entonces el grupo de puntos es C nv. Si ese no es el caso, preguntamos si hay un S 2n además del C n. En caso afirmativo, el grupo de puntos es S 2n. Si no es así, es C n.
Ejemplo: Dibromonaftaleno
Practicemos la guía del grupo de puntos con un ejemplo. Veamos la molécula de dibromonaftaleno (Fig. 2.2.87).
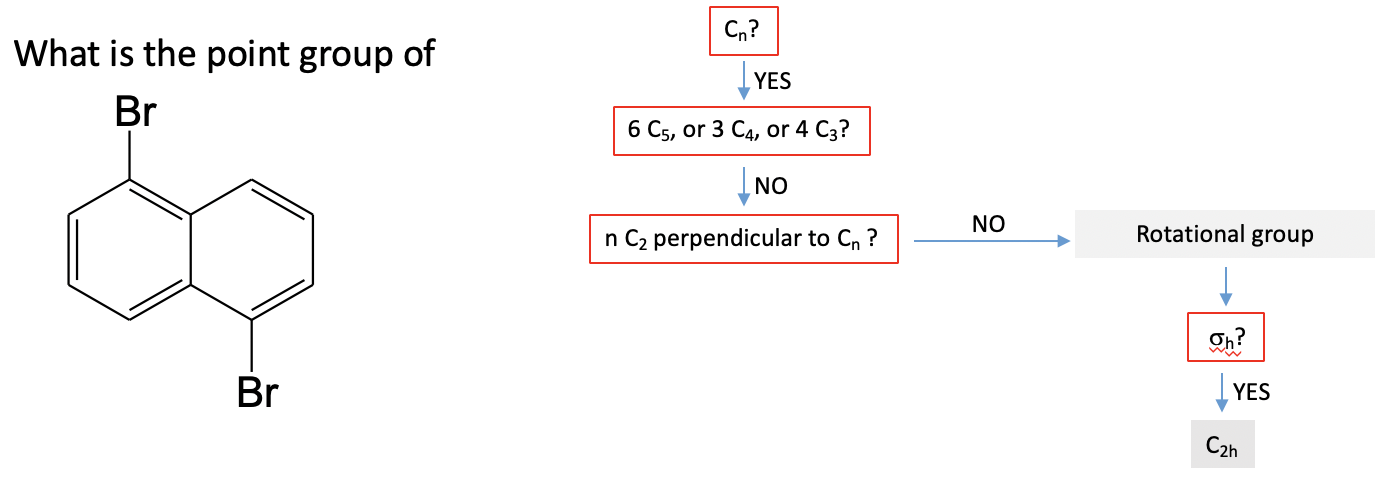
La primera pregunta que haríamos es: ¿Se puede ver al menos un eje rotacional adecuado? La respuesta es sí. Hay un eje de rotación apropiado C 2 que se encuentra perpendicular al plano de la molécula y pasa por el centro del enlace C-C que es compartido por los dos anillos aromáticos. A continuación preguntamos: ¿Son los ejes 6C 5, 3C 4 o 4C 3? Claramente ese no es el caso, y por lo tanto no tenemos un grupo de puntos de simetría alta. A continuación podemos pensar si los hay 2C 2 ejes además de los ejes C 2 que ya encontramos. La respuesta es no, por lo que el grupo puntual no puede ser un grupo diedro. A continuación, pediríamos: ¿Hay un plano espejo horizontal? Este es efectivamente el caso. Hay un plano espejo horizontal en el plano de la molécula. No mueve ningún átomo alrededor, pero como discutimos antes, un espejo no necesita hacer esto para existir. Esto identifica al grupo de puntos como C 2h.
Grupos de puntos quirales
Un grupo de puntos quirales es un grupo de puntos que solo tiene operaciones de rotación adecuadas además de la identidad. Esto equivale a la afirmación de que no deben existir rotaciones impropias en un grupo de puntos quirales. Esto incluye planos de espejo y centros de inversión porque un plano espejo es lo mismo que un S 1, y un centro de inversión es lo mismo que un S 2. Si una molécula pertenece a un grupo puntual quiral, entonces tiene una imagen especular que no puede superponerse con la molécula original. Las dos imágenes especulares se llaman enantiómeros. Un ejemplo es el bromoclorofluorometano. Se pueden ver dos enantiómeros separados por una línea punteada (Fig. 2.2.88).
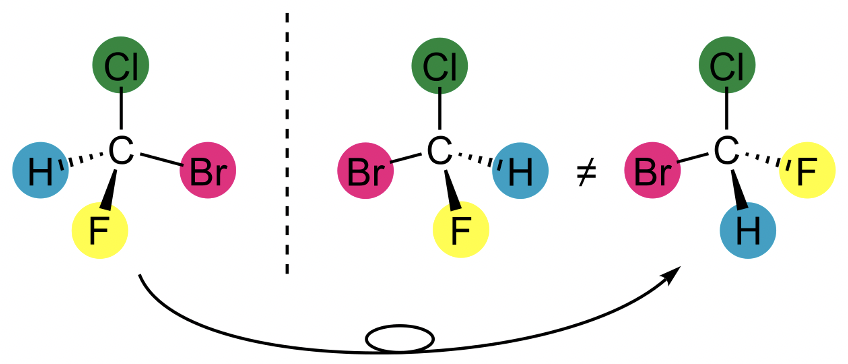
La línea punteada representa un plano espejo. Tenga en cuenta que este plano espejo no es un plano espejo en el sentido de un elemento de simetría. Se puede ver que las dos moléculas a la izquierda y a la derecha del plano espejo son imágenes especulares respectivas entre sí. Las moléculas no pueden superponerse, lo que significa que son enantiómeros. Tenga en cuenta que la molécula de bromoclorofluorometano en el extremo derecho no es un enantiómero a los otros dos. Es la misma molécula que el enantiómero en el extremo izquierdo. Solo necesitamos rotar en el sentido de las agujas del reloj alrededor del eje C-Cl para hacer que las dos moléculas se superpongan, lo que significa que son iguales.
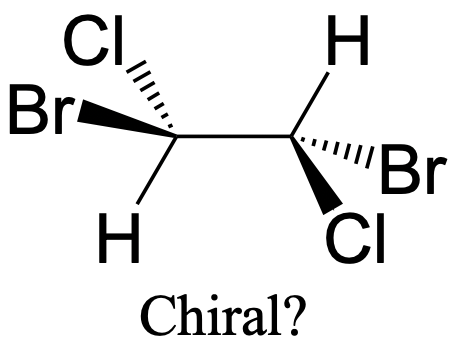
Cabe señalar que el hecho de que una molécula tenga un carbono con cuatro sustituyentes diferentes no es suficiente para convertirla en una molécula quiral. La molécula de dibromodicloroetano mostrada anteriormente (Fig. 2.2.89) tiene cuatro sustituyentes diferentes alrededor del átomo de carbono, pero no es quiral porque hay un centro de inversión en medio del enlace C-C.
Grupos de puntos de alta simetría quirales
Los grupos quirales no necesariamente necesitan tener baja simetría, de hecho, los subgrupos rotacionales de alta simetría I, O y T son grupos quirales porque solo tienen ejes adecuados además de la identidad (Fig. 2.2.90).
