3.1: Introducción a la Teoría Orbital Molecular
- Page ID
- 70179
Enlace covalente: teoría orbital molecular
Ahora que hemos estudiado a fondo la simetría, a continuación podemos aplicar la simetría a la teoría orbital molecular. La teoría orbital molecular es una teoría de unión que se ha desarrollado para explicar el enlace covalente, pero como veremos en un poco, también puede hacer declaraciones sobre el enlace iónico. Veremos que la aplicación de la simetría a la teoría orbital molecular nos ayudará en gran medida a comprender los orbitales moleculares, en particular para moléculas más complejas. Antes de aplicar la simetría a la teoría orbital molecular, sin embargo, revisemos brevemente los principios de la teoría orbital molecular.
Como todas las teorías se basa en unos supuestos básicos, también llamados axiomas. El primer supuesto es la aproximación Born-Oppenheimer. Dice que la posición de los núcleos está casi fija en relación con el movimiento de los electrones (Fig. 3.1.1).

Esta es una buena aproximación porque los núcleos son mucho más masivos que los electrones. El segundo axioma es que los orbitales moleculares pueden describirse como una combinación lineal de orbitales atómicos (Fig. 3.1.2). Combinación lineal significa una suma o resta vectorial.
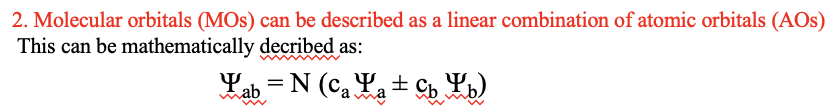
Dado que los orbitales son las llamadas funciones vectoriales, se pueden sumar y restar como vectores. Cualquier orbital es una función de onda que tiene una amplitud específica en un punto particular del espacio. Un punto en el espacio se define por un vector que apunta desde el origen hasta ese punto en el espacio. Por lo tanto, existe una amplitud asociada a cada vector que se asocia con la función de onda. En forma matemática podemos decir que un orbital molecular ψ ab = N (c a ψ a ± c b ψ b), donde ψ a es el orbital atómico a del átomo a, y ψ b es el orbital atómico b del átomo b. Los coeficientes c a y c b determinan cuánto contribuyen los orbitales atómicos específicos a y b a los orbitales moleculares. Cuanto mayor sea el coeficiente, mayor será la contribución del orbital atómico particular al orbital molecular.
N es el llamado factor de normalización. El factor de normalización tiene un valor de manera que la probabilidad de encontrar el electrón en cualquier lugar dentro del orbital molecular es del 100%. Al igual que en los orbitales atómicos, el cuadrado de la función de onda para un orbital molecular refleja la probabilidad de encontrar el electrón en una posición particular, cuando vemos al electrón como una partícula. Por lo tanto, la integral del cuadrado de la función de onda sobre el espacio debe ser 1, y se elige el factor de normalización para que sea 1. El número de orbitales que se pueden combinar con orbitales moleculares no se limita a dos. También se pueden combinar tres, cuatro o más orbitales. El número de orbitales moleculares que resulta de una combinación de orbitales atómicos es siempre la suma de los orbitales atómicos. Entonces, cuando se combinan dos orbitales atómicos, deben resultar dos orbitales moleculares, cuando se combinan tres orbitales atómicos, deben resultar tres orbitales moleculares, y así sucesivamente.
¿Cómo podemos entender cualitativamente que la adición vectorial de orbitales atómicos para formar orbitales moleculares explica la unión covalente? La naturaleza del enlace covalente es que los electrones están siendo compartidos entre ellos y que los enlaces son direccionales. Si acercamos dos orbitales atómicos, comenzarán a interferir.
Por ejemplo, dos orbitales 1s de dos átomos de hidrógeno comenzarán a interferir a medida que acerquemos los dos átomos. Si esa interferencia es constructiva entonces las amplitudes de las dos funciones de onda se sumarán y resultarán en un aumento de la amplitud entre los átomos. Esta adición de amplitudes se puede describir matemáticamente mediante la adición vectorial de las amplitudes orbitales atómicas. Una amplitud incrementada se asocia con una mayor densidad de electrones entre los átomos. Debido a que esta densidad electrónica se encuentra entre los átomos, puede interpretarse como densidad electrónica “compartida” explicando un enlace direccional y covalente. El orbital molecular puede denominarse orbital molecular de enlace (Fig. 3.1.3).

Figura 3.1.3 B onding orbital molecular de los orbitales 2s de dos átomos de hidrógeno (Atribución: www.falstad.com/qmmo/)
Sin embargo, también debemos considerar que pueden producirse interferencias negativas que pueden describirse mediante sustracción vectorial de las amplitudes de los orbitales atómicos. En este caso la densidad de electrones se agota entre los átomos, y en realidad hay un nodo entre los átomos donde la función de onda del orbital molecular cambia su signo algebraico. Este orbital molecular puede denominarse orbital molecular antienlace (Fig. 3.1.4).

El orbital antienlace tiene una energía más alta que el orbital molecular de unión. Esto se puede entender cualitativamente a partir del hecho de que la energía de las funciones de onda aumenta con el número de nodos. Hemos visto este principio antes cuando discutimos la teoría atómica, y ahora lo volvemos a encontrar en la teoría orbital molecular. Si se forma un enlace covalente dependerá cuántos electrones estarán en los orbitales de enlace o antienlace.
Los electrones tienden a ocupar primero los estados de menor energía y, por lo tanto, los orbitales de unión se llenarán primero. Sin embargo, el principio Pauli se mantiene para los orbitales moleculares como para los orbitales atómicos, y por lo tanto no podemos llenar más de dos electrones en un orbital molecular. Una vez que se llena el orbital molecular de unión, debemos comenzar a llenar el orbital antienlace.

Podemos definir un orden de enlace en la molécula restando el número de electrones en orbitales antienlace del número de orbitales de unión, y dividir el número resultante por dos (Fig. 3.1.5).
Si nos atenemos a nuestro ejemplo, los dos átomos de H, entonces tenemos dos electrones en general a considerar. Podemos llenar ambos electrones en el orbital molecular de unión, y el orbital molecular antienlace permanece vacío. Esto da un orden de enlace de (2-0) /2=1. Por lo tanto, podemos decir que se ha formado un enlace covalente entre los átomos de H, hemos producido una molécula H 2.
Generalmente podemos decir que una molécula esperaría que fuera estable cuando el orden de enlace es mayor a 0. Eso significaría que un ion molecular H 2 + debería ser estable porque su orden de enlace sería (1-0) /2=½. El ion H 2 + tiene solo un electrón que estaría en el orbital de unión. Sin embargo, este orden de enlace es menor que el de H 2, y por lo tanto debe ser menos estable que H 2. Esto está de acuerdo con las observaciones experimentales. También un ion H 2 - debe ser estable. En este caso, uno de los tres electrones globales estaría en el orbital antienlace. El orden de fianza sería (2-1) /2=1/2. Un anión H 2 -, sin embargo, se esperaría que fuera inestable debido a que habría dos electrones en orbitales moleculares de enlace, y dos en los antienlaces, dando como resultado un orden de enlace de (2-2) /2=0 (Fig. 3.1.6).
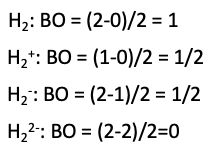
Diagrama orbital molecular de H 2
El enlace covalente en una molécula puede describirse mediante un diagrama orbital molecular. Revisemos brevemente los principios de su construcción para el ejemplo de la molécula H 2 (Fig. 3.1.7).
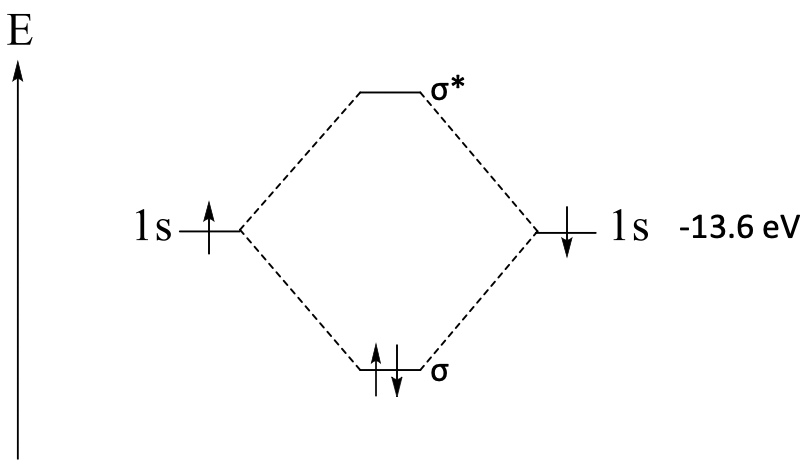
En primer lugar, escribimos una flecha a la izquierda. Indica las energías relativas de los orbitales, y está etiquetada con una E, que significa energía.
A continuación, indicamos los dos orbitales atómicos 1s por dos líneas horizontales, y les damos etiquetas apropiadas. Las líneas deben estar en los mismos niveles de energía en el diagrama, ya que ambos orbitales 1s tienen la misma energía. Si conoces la energía exacta de los orbitales puedes escribir la energía exacta junto al nombre orbital. En el caso de los orbitales 1s esto sería de -13.6 eV.
A continuación escribimos los dos orbitales moleculares como líneas horizontales a los niveles de energía apropiados en la mitad del diagrama. El orbital de unión debe tener una energía menor que los orbitales atómicos, y el orbital antienlace debe tener una energía mayor. La diferencia energética entre los orbitales moleculares y los orbitales atómicos debe ser aproximadamente la misma. Por lo general, el orbital de unión es ligeramente menor que el orbital antiunión es antiunión. Al construir diagramas orbitales moleculares cualitativos, no conocemos los valores exactos de energía para los orbitales moleculares, pero podemos estimar las energías relativas de los orbitales de acuerdo con los argumentos que acabamos de discutir. En el caso de la molécula H 2 los dos orbitales atómicos 1s se superponen de manera σ-moda, por lo tanto, podemos denotar los orbitales moleculares con un símbolo σ que podemos escribir junto a las líneas para los orbitales. El MO antiadherencia obtiene un * además de indicar su naturaleza antiadherencia. Conectamos los orbitales moleculares con orbitales atómicos mediante líneas punteadas para indicar que los orbitales moleculares se han construido a partir de los orbitales atómicos 1s.
En el último paso, llenamos los electrones en los orbitales atómicos y moleculares. Cada hidrógeno tiene un electrón 1s, y escribimos los electrones como flechas en los orbitales 1s. Un electrón debe ser spin up y el otro spin down, porque los electrones deben tener espines pareados en el orbital molecular, y la inversión de espín está prohibida quantomecánicamente. Por último, llenamos los dos electrones en los orbitales moleculares según la energía. Esto significa que debemos escribirlos con espines emparejados en el orbital molecular de unión. Ahora nuestro diagrama orbital molecular está completo.
Factores que influyen en el grado de interacción covalente
Ahora refinemos nuestra comprensión de los orbitales moleculares y los diagramas orbitales moleculares. No todos los orbitales atómicos pueden combinarse para formar orbitales moleculares, y el grado de interacción covalente entre dos orbitales atómicos puede variar mucho. ¿Cuáles son los criterios según los cuales podemos decidir si la interacción covalente entre dos orbitales atómicos es posible, y de ser así, cuánto? Hay tres criterios a considerar.
El criterio de simetría, el criterio de superposición y el criterio de energía. El criterio de simetría dice que si hay una combinación de orbitales atómicos con enlace y las interacciones antiadhesión que no cancelan entonces hay una interacción de unión. Discutiremos en un momento lo que esto significa.
Definición: Criterio de simetría
Si hay una combinación de orbitales atómicos con enlaces y las interacciones antiadhesión que no cancelan entonces hay una interacción de unión.
El criterio de superposición establece que cuanto mejores sean los orbitales atómicos (¡de simetría apropiada!) se superponen cuanto más fuerte es la interacción covalente.
Definición: Criterio de superposición
Cuanto mejores sean los orbitales atómicos (¡de simetría apropiada!) se superponen cuanto más fuerte es la interacción covalente.
El criterio energético establece que cuanto más cerca están los orbitales en energía, más interacción covalente entre ellos.
Definición: Criterio Energético
Cuanto más cerca están los orbitales atómicos en energía, más fuerte es la interacción covalente.
El criterio de superposición
Veamos ahora cada criterio con más detalle. Empecemos por el que probablemente podamos entender más fácilmente, el criterio de superposición. Cuanto mayor sea el solapamiento, mayor será la interacción covalente. El solapamiento se puede estimar de acuerdo a tres reglas.
Regla 1
La primera regla dice que el solapamiento es cuanto mayor menor es la distancia entre los dos orbitales (Fig. 3.1.8).

Esto significa que una pequeña distancia entre el orbital conduce a un orbital fuertemente unido y uno fuertemente antienlace, respectivamente, mientras que una gran distancia conduce a un orbital débilmente unido y un orbital débilmente antienlace. Cuando la distancia es pequeña entonces hay una gran diferencia de energía entre el enlace y el orbital molecular antienlace, cuando la distancia es grande entonces la diferencia de energía es pequeña (Fig. 3.1.9).
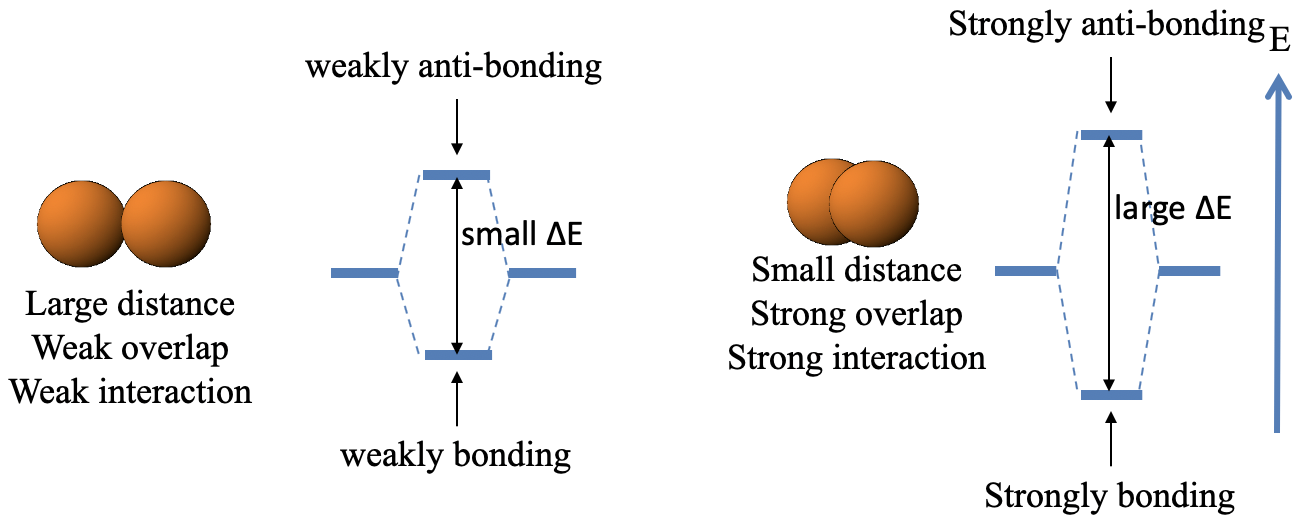
Regla 2
La regla 2 establece que un orbital grande “difuso” tiende a superponerse mejor (interactúa más fuertemente) con otro orbital cuando este orbital es también un orbital difuso grande. Orbitales pequeños “poco difusos” tienden a interactuar más fuertemente con otros orbitales poco difusos. Sin embargo, si combinamos un orbital grande con un orbital pequeño, entonces esto normalmente no conduce a una buena superposición y, por lo tanto, a una interacción débil (Fig. 3.1.10).

Esto lo podemos entender cualitativamente mirando la imagen de abajo (Fig. 3.1.11).
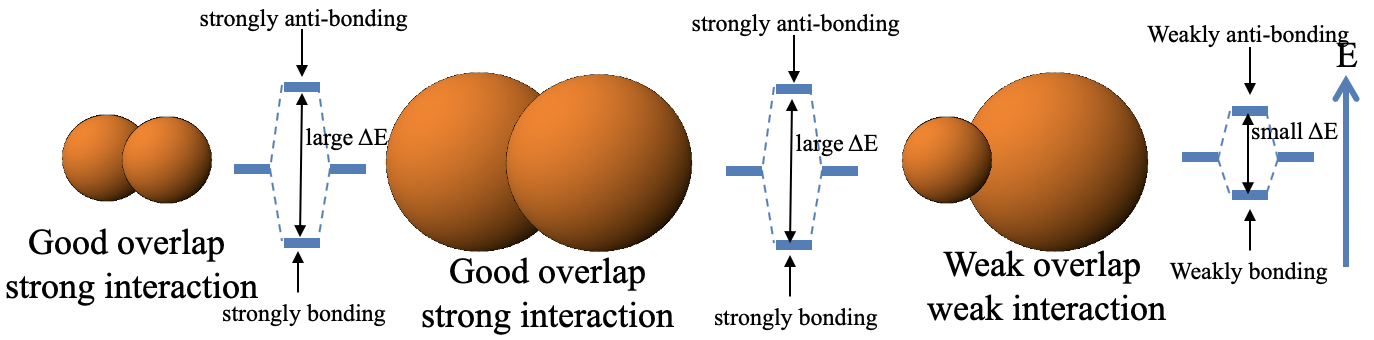
Solo una pequeña fracción de volumen de la órbita grande puede superponerse con la órbita pequeña debido al pequeño tamaño de la órbita pequeña. Debido a esa pequeña superposición, el orbital de unión solo se une débilmente, y el antienlace solo es débilmente antiunión. La diferencia de energía entre la unión y la órbita antiunión es pequeña. En los otros dos casos, los orbitales de unión tienden a estar fuertemente unidos, y los antiadhesión fuertemente antiadhesión. Las diferencias de energía entre los orbitales tienden a ser grandes.
Regla 3
La regla 3 dice que los orbitales que se superponen de manera σ-tienden a interactuar más fuertemente que los orbitales que se superponen en forma π (Fig. 3.1.12).

Se puede ver fácilmente en la imagen de abajo que dos orbitales p que tienen la misma distancia d entre sí se superponen mucho más cuando se superponen de manera σ-en comparación con la moda π (Fig. 3.1.13).
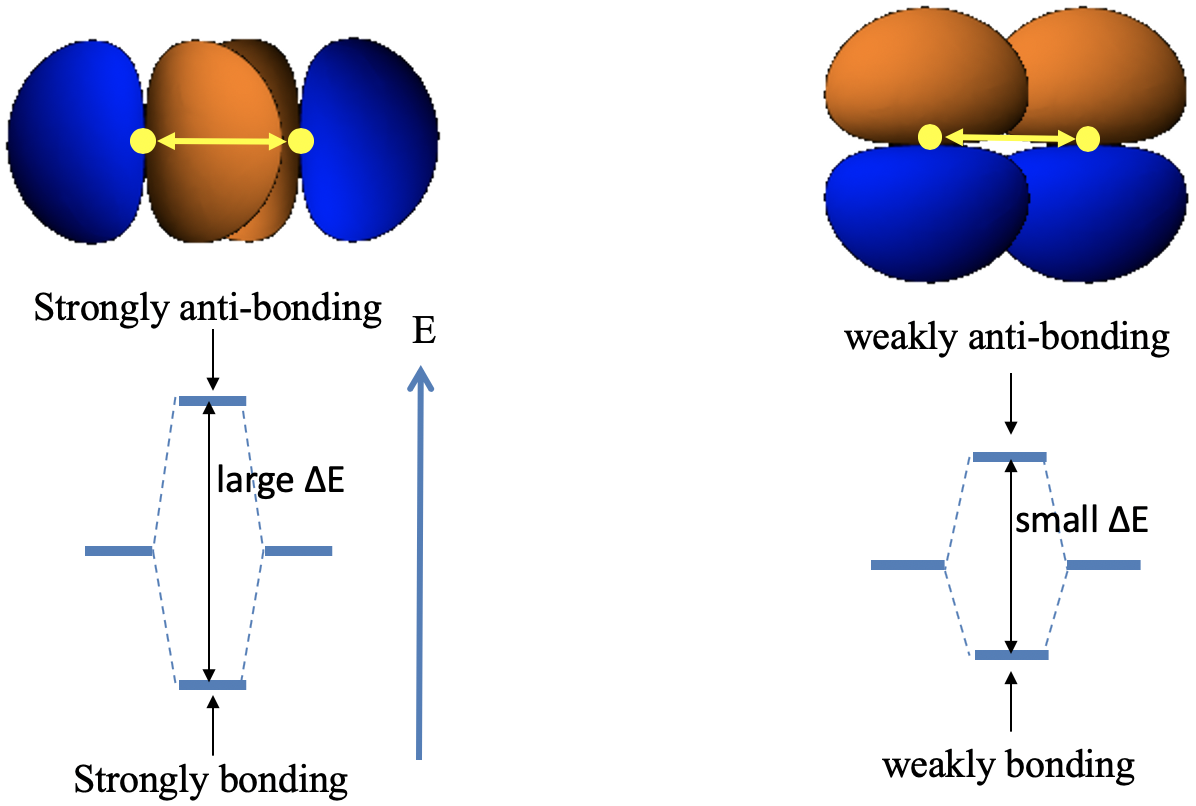
Esto se debe a que en el primer caso apuntan uno hacia el otro, y el solapamiento orbital está en el eje de enlace, mientras que en este último caso están orientados paralelos entre sí, y el solapamiento orbital está por encima y por debajo del eje de enlace. Esto implica que el solapamiento σconduce a más orbitales de unión y antiunión con un mayor espacio de energía entre ellos en comparación con el solapamiento π.
El Criterio Energético
El criterio energético establece que la interacción covalente es cuanto mayor es la menor es la diferencia de energía entre los orbitales atómicos. Podemos entender esto cualitativamente al considerar que los orbitales son ondas, y las ondas de energía similar interfieren más significativamente entre sí que las ondas con diferentes energías. Solo imagina dos ondas con longitudes de onda muy diferentes asociadas a energías muy diferentes. ¿Interfirirían efectivamente? No, no lo harían Más bien, dos ondas con longitudes de onda muy similares interferirían mejor. Debido a que una mayor diferencia de energía significa menos interacción, los orbitales moleculares que resultan de la interacción de dos orbitales atómicos con una gran diferencia de energía son mucho más similares en forma, tamaño y ubicación en comparación con los orbitales moleculares que resultan de orbitales atómicos con energía similar.
La mayor interacción covalente se espera cuando la energía entre los dos orbitales es exactamente la misma. Esto sólo es posible cuando dos, mismos orbitales A de los dos mismos átomos se superponen. En este caso formamos un enlace covalente perfecto con electrones exactamente iguales compartidos entre los orbitales. El máximo de la amplitud del orbital molecular de enlace está exactamente en el medio entre los dos átomos. En el diagrama orbital molecular la diferencia de energía entre el MO de unión y los AO es aproximadamente la misma que la diferencia de energía entre el MO antienlace y los AO. Suponiendo que cada orbital atómico está lleno de un electrón, los dos electrones están en el orbital molecular de enlace donde están igualmente compartidos entre los átomos (Fig. 3.1.14)
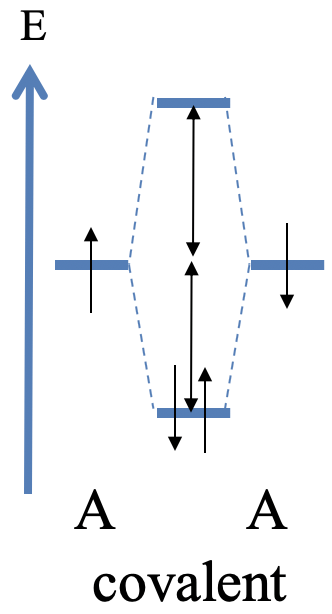
Ahora hagamos algo diferente la energía de los dos orbitales atómicos. Debido a que son diferentes, ahora denotamos los orbitales atómicos A y B, por lo que elegimos que la energía de la órbita A sea algo mayor que la del orbital B. La superposición entre el orbital atómico todavía produce interacción covalente que produce un orbital molecular de enlace y un orbital molecular antienlace. Sin embargo, la diferencia de energía de los orbitales moleculares a los dos orbitales atómicos ya no es la misma. El MO antiadhesión ahora está más cerca del AO con la mayor energía, y el MO de unión ahora está más cerca en energía al AO con la energía más baja. Esto tiene otra consecuencia. El orbital molecular de enlace ahora se localiza principalmente en el átomo B, y el orbital antienlace se localiza principalmente en el átomo A. Si nuevamente asumimos que cada AO aportó un electrón al enlace covalente, entonces los dos electrones estarán en el MO de enlace. Debido a que el MO de enlace ahora se localiza principalmente en el átomo B, los electrones de unión se localizan principalmente en el átomo B. Esto significa que ya no son exactamente iguales compartidos, y tenemos un enlace polar covalente que polarizó hacia el átomo B (Fig. 3.1.15).
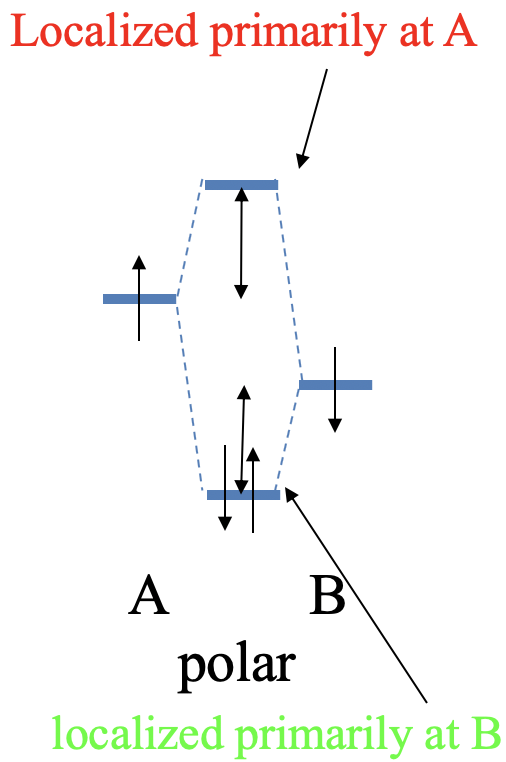
Ahora hagamos muy grande la diferencia energética entre los dos orbitales atómicos de los átomos A y B (Fig. 3.1.16). En este caso, el MO de unión está energéticamente muy cerca del AO del átomo B, y se localiza casi exclusivamente en el átomo B. En realidad, el MO de unión se asemeja mucho al AO del átomo B en forma, tamaño y localización. Es decir, el AO de B apenas ha cambiado debido a la muy débil interacción covalente resultante de la gran diferencia de energía entre los orbitales atómicos. Por el contrario, el orbital antienlace está energéticamente muy cerca del AO del átomo A, y se localiza casi por completo en el átomo A. El MO antienlace está muy cerca del AO en forma, tamaño y ubicación. Debido a la débil interacción covalente, casi no hay cambio en el orbital atómico de A. Suponiendo que cada orbital atómico aporta dos electrones, el orbital de enlace se llenará. Los dos electrones se ubicarán casi exclusivamente en el átomo B. Esto significa que efectivamente hemos transferido un electrón del átomo A al átomo B en un proceso redox, y hemos producido un enlace iónico. El átomo A tiene ahora efectivamente una carga 1+, y el átomo B tiene una carga 1-. Esto demuestra que la teoría orbital molecular, aunque diseñada para la unión covalente, también puede hacer declaraciones sobre el enlace iónico. También podemos ver que un enlace 100% iónico no es posible. Para lograr el 100% de iconicidad la diferencia de energía entre los dos orbitales atómicos tendría que ser infinitamente grande. Esto es prácticamente imposible. Sin embargo, un enlace covalente al 100% es posible porque dos electrones pueden compartirse exactamente por igual entre dos átomos cuando la energía de los orbitales atómicos es exactamente cero.
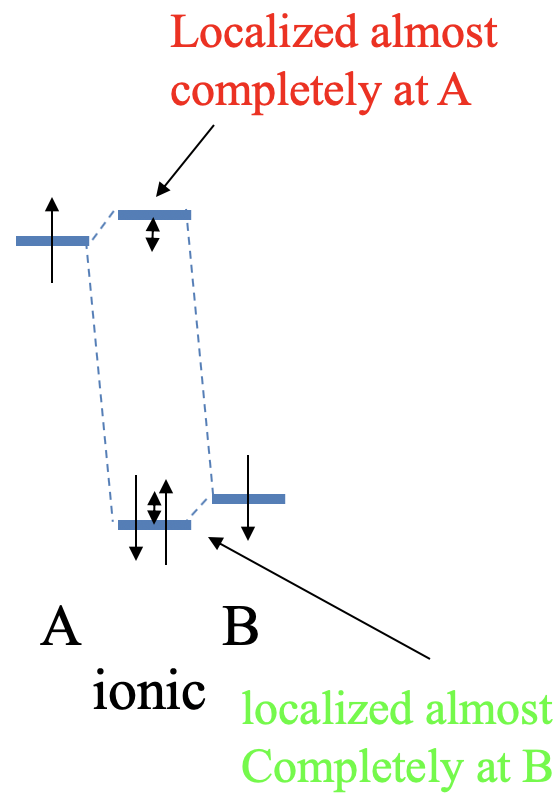
Otra conclusión que podemos sacar es que los electrones de unión se localizan en el átomo con el orbital atómico de menor energía, y los electrones antienlace se localizan en los átomos con el orbital atómico de mayor energía. La energía orbital se correlaciona con la electronegatividad. Para orbitales del mismo tipo y los mismos elementos, los orbitales con mayor electronegatividad tienen menor energía. Por ejemplo, un orbital 2s de flúor tiene una energía menor que una orbital 2s de oxígeno debido a que la electronegatividad del flúor es mayor. Por lo tanto, los electrones de unión se localizan principalmente en el átomo más electronegativo, mientras que los electrones antienlace se localizan principalmente en el átomo menos electronegativo (Fig. 3.1.7). Cuando hay suficientes orbitales antienlace ocupados es posible que la polaridad global en la molécula sea tal que el momento dipolar apunte hacia el átomo más electro-positivo. Un ejemplo es el monóxido de carbono que está ligeramente polarizado hacia el átomo de carbono. Discutiremos el diagrama MO del monóxido de carbono en detalle más adelante.
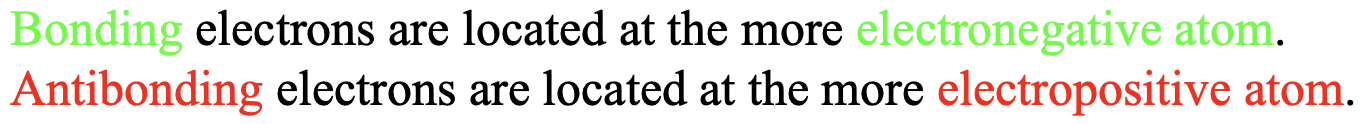
El criterio de simetría
Por último, veamos el criterio de simetría. El criterio de simetría nos indica si es posible una interacción covalente entre orbitales basada en la orientación relativa de los orbitales. Solo si las interacciones de unión y antiunión no se cancelan, es posible una interacción de unión, y podemos construir orbitales moleculares a partir de orbitales atómicos. Las interacciones de unión y antiunión se cancelan cuando las interferencias positivas y negativas debidas a la superposición orbital son exactamente iguales. Esto se puede determinar mediante la inspección del solapamiento orbital.
Por ejemplo, veamos el solapamiento orbital entre los orbitales 1s de hidrógeno y el orbital 2p z de oxígeno en la molécula de agua (Fig. 3.1.18).
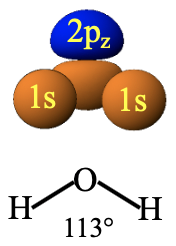
En la molécula de agua los orbitales están orientados entre sí de una manera específica debido a la estructura doblada de la molécula de agua. Debido a la estructura doblada de la molécula de agua, los orbitales 1s se superponen de manera diferente con los dos lóbulos de la molécula 2p z. El lóbulo que apunta hacia abajo se solapa con mayor fuerza que el lóbulo que apunta hacia arriba. Los dos lóbulos deben tener diferente signo algebraico. Ahora elegimos los cantos algebraicos de los orbitales 1s para que se maximice la vinculación. Esto significa que elegimos los signos algebraicos para que sean los mismos que los del lóbulo que apunta hacia abajo. Podemos ver que ahora el solapamiento de los 1s con el orbital 2p z produce interferencias más positivas que negativas. El lóbulo azul está más alejado de los orbitales 1s que el lóbulo naranja y, por lo tanto, las interferencias positivas y negativas no se cancelan. Esto equivale a decir que las interacciones bonding y anti-bonding no cancelan. Por lo tanto, la simetría es “correcta”, podemos construir orbitales moleculares a partir de esta combinación de orbitales atómicos.
¿Puede el orbital 2p x de oxígeno también combinado con los orbitales 1s del átomo de hidrógeno para formar orbitales moleculares? El orbital 2p x está orientado de manera diferente en relación con los orbitales 1s en la molécula H 2 O (Fig. 2.1.19).
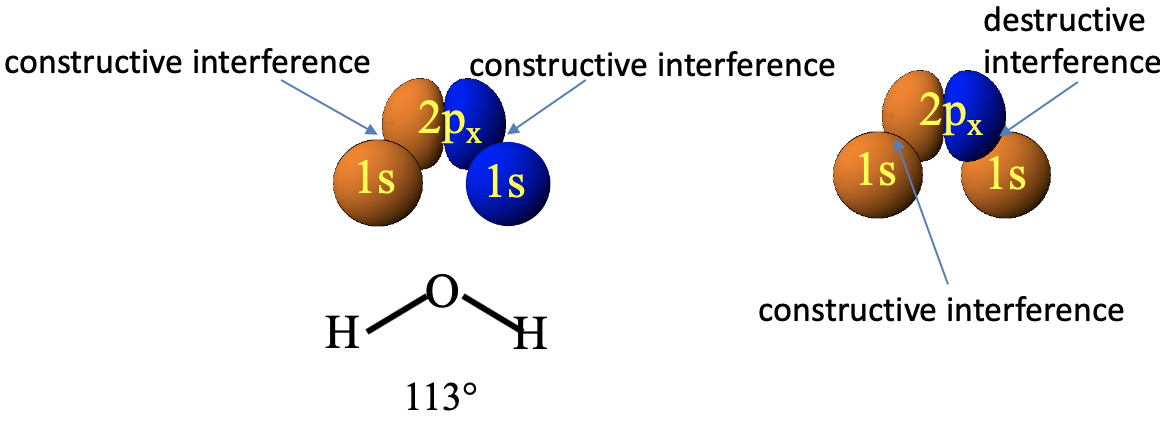
En este caso, debemos elegir los signos algebraicos de los dos orbitales 1s para que sean diferentes para que las interacciones de unión sean posibles. Las interacciones de unión y antiunión solo no cancelan si el orbital 1s izquierdo tiene el mismo signo algebraico que el lóbulo izquierdo del orbital 2p x y el orbital 1s derecho tiene el mismo signo algebraico que el lóbulo derecho del orbital 2p x. Si, por ejemplo, elegimos ambos orbitales 1s para ser anaranjados, entonces las interacciones de unión entre el lóbulo izquierdo y el orbital 1s izquierdo serían canceladas por las interacciones anti-unión igualmente fuertes entre el lóbulo derecho y el orbital 1s derecho. En general, vemos sin embargo, que si seleccionamos el color (que significa signo algebraico) de los orbitales 1s apropiadamente entonces la simetría es “correcta” y podemos crear orbitales moleculares a partir de los orbitales atómicos.
¿Y la combinación de los 2s del oxígeno con los orbitales 1s de los hidrógenos (Fig. 3.1.20)?
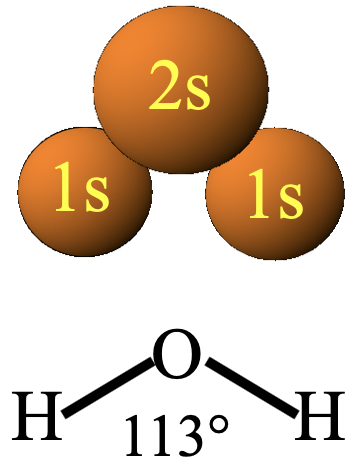
Podemos ver que es muy fácil construir una combinación en la que haya interacciones vinculantes. Si elegimos que el signo algebraico de todos los átomos sea el mismo, entonces ciertamente las interacciones de unión y antiunión no cancelan. La simetría es “correcta”, y la construcción de orbitales atómicos a partir de orbitales moleculares es posible.
¿Qué pasa con las interacciones entre los orbitales 1s y el orbital 2p y (Fig. 3.1.21)?
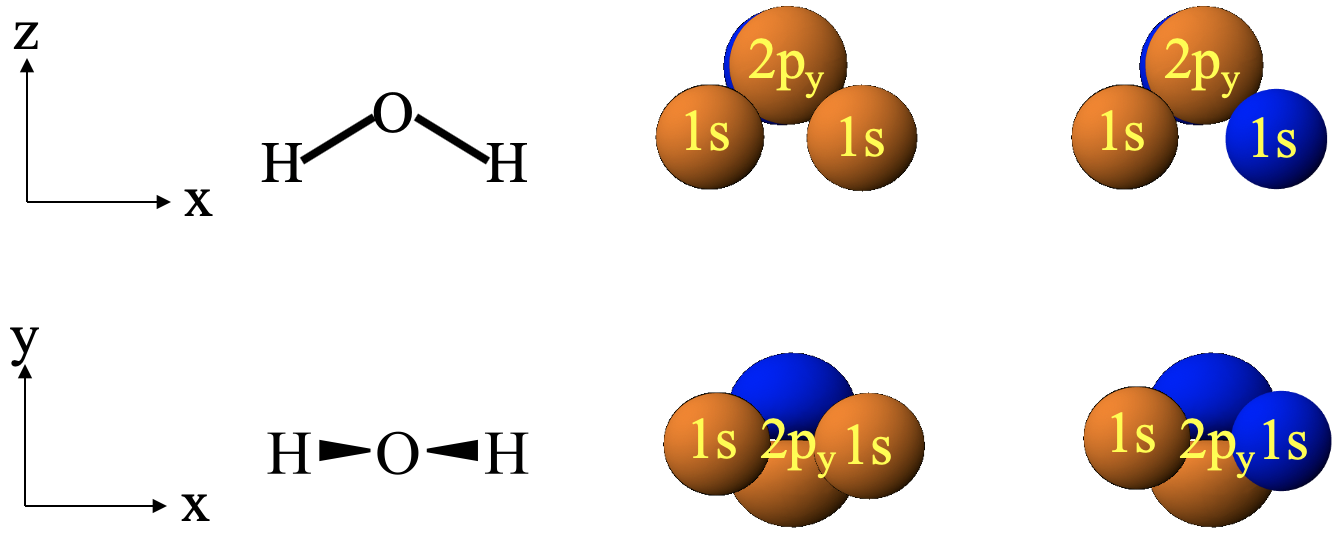
En este caso, los dos orbitales 1s están en el plano de papel, y el orbital 2p y se encuentra perpendicular a él. Eso hace que un orbital 1s se superponga por igual con ambos lóbulos del orbital 2p y. Debido a que los dos lóbulos de un orbital 2p y deben tener un signo algebraico diferente, las interferencias constructivas y destructivas se cancelarán, no importa cómo elegimos los signos algebraicos de nuestros orbitales 1s. Eso significa que no hay posibilidad de crear solapamiento orbital en el que las interacciones de unión y antienlace no se cancelen. Por lo tanto, no podemos producir orbitales moleculares a partir de una combinación de orbitales 1s y 2p y. El 2p y debe permanecer sin unión. Es posible que pueda ver mejor la cancelación de la superposición orbital de unión y antiadhesión si elige su sistema de coordinación de manera diferente. Hagamos que el eje y apunte hacia arriba, y el eje x apunte a la derecha (Fig. 3.1.21, abajo). Ahora observamos la molécula H 2 O desde la perspectiva de las aves, y el orbital 2p y está orientado verticalmente. Los orbitales 1s siguen en el eje x. Ahora se puede ver más claramente el solapamiento entre los orbitales 1s y el orbital 2p y. No importa cómo elijamos el signo algebraico de nuestros orbitales, las interacciones de unión y antivinculación se cancelan.
Hemos visto hasta ahora que es posible decidir sobre simetrías “correctas” e “incorrectas” por inspección, pero hemos notado que esto no es trivial. Generalmente, cuanto más compleja se vuelve una molécula, más difícil es decidir sobre la simetría “correcta” y “incorrecta”. Como veremos a continuación, la teoría de grupos puede ayudarnos en gran medida a decidir sobre la simetría “correcta” y “incorrecta”. Proporciona un camino formal para tomar sin ambigüedades tal decisión.


