8.2: División de términos en campos de ligandos, reglas de selección, diagramas Tanabe-Sugano. Transiciones de metal a ligando y ligando a metal
- Page ID
- 70205
División de términos en un campo octaédrico

Hasta ahora solo hemos considerado términos de iones libres, es decir, términos sin la presencia de un campo ligando. Pensemos a continuación en la influencia de un campo octaédrico en un término. Los términos son ondulaciones, al igual que los orbitales, y por lo tanto se comportan como orbitales en un campo de ligandos. Los orbitales D se dividieron en orbitales t 2g y e g en un campo de ligando octaédrico. Un término D se comporta de manera similar. Se divide en términos T 2g y E g. Los orbitales P son triple-degenerados teniendo simetría T 1g en el grupo puntual O h y no se dividen en energía. Los términos P tienen la misma simetría y tampoco se dividen. Podemos llamar a un término P en un campo de ligando octaédrico un término T 1g. Siguiendo argumentos análogos, los términos S se convierten en términos A 1g. Los términos F se dividen en energía como orbitales f y se convierten en términos T 1g, T 2g y A 2g. En general, la presencia del campo octaédrico incrementa el número de términos de cuatro a siete (Fig. \(\PageIndex{1}\)). Es fácil ver que el campo del ligando conduce a muchos estados, y muchas transiciones potenciales de electrones. Así, esperaríamos espectros bastante complicados. Para otros campos de ligandos, los términos también se comportan de manera análoga a los orbitales. Por ejemplo, en un campo tetraédrico los términos D se dividen en términos E y T 2, y así sucesivamente.
División a término para complejos metálicos octaédricos d 2
Ahora pensemos en cómo cambia el término energías de nuestro ion d 2 libre cuando se coloca en un campo ligando octaédrico, dependiendo de la fuerza del campo del ligando. Podemos expresarlo mediante un diagrama de correlación (Fig. 8.2.2). En un diagrama de correlación, trazamos las energías de los términos relativos a la intensidad de campo.
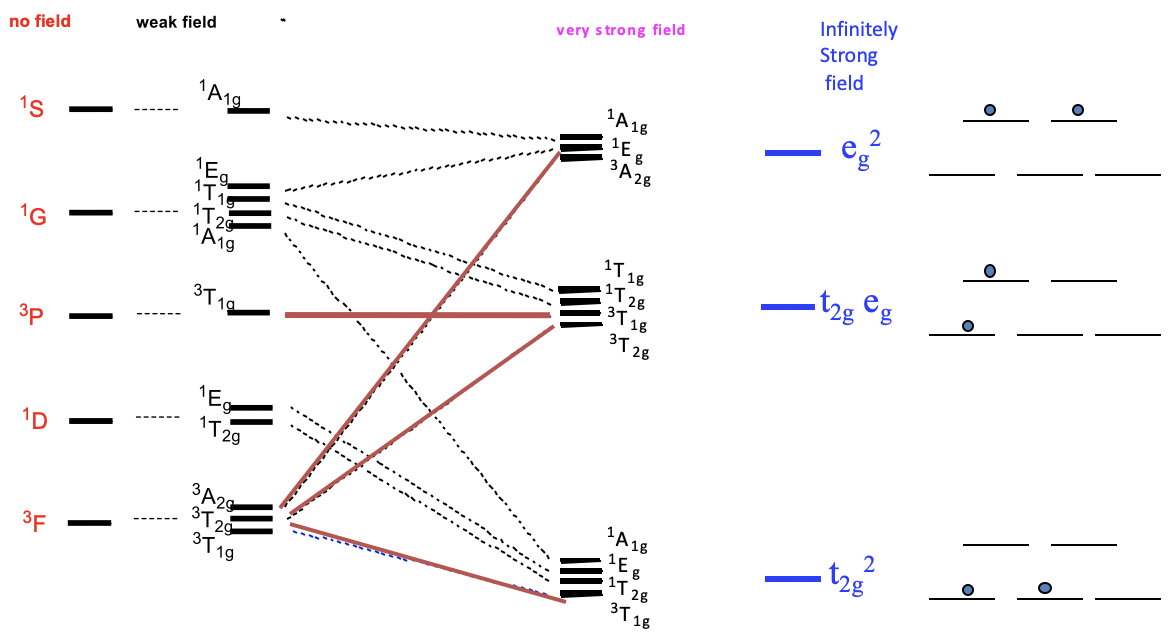
En el lado izquierdo trazamos los términos sin ningún campo de acuerdo a sus energías. En el caso de un ion d 2, las energías son 3 F< 1 D< 3 P< 1 G< 1 S. A continuación, trazamos las energías relativas en un campo de ligando octaédrico débil, y etiquetamos los términos según su simetría. Podemos ver que los términos D, F y G se dividen en energía, mientras que los términos S y P no lo hacen. Debido al campo débil, las diferencias de energía son muy pequeñas. Ahora aumentemos la fuerza del campo del ligando continuamente, hasta que hayamos alcanzado un campo de ligando muy fuerte. Vemos que algunos de los términos se mueven hacia arriba en energía, mientras que otros términos bajan a medida que aumenta el campo de ligandos. Por ejemplo, dos de los tres términos resultantes de los términos F aumentan en energía mientras que uno disminuye. También es posible que un término no cambie su energía. Por ejemplo, el término 3 T 1g del término 3 P no cambia su energía. En campo ligando muy fuerte hay tres grupos de términos que tienen energía similar. En el caso hipotético de un campo ligando infinitamente fuerte, los términos que pertenecen a un grupo particular se vuelven idénticos en energía. En este caso, sólo hay tres estados para los electrones posibles. El campo se considera tan fuerte por lo que la energía asociada a las interacciones electrón-electrón se vuelve insignificante en comparación con la energía del campo. Los electrones se comportan como si no hubiera interacciones electrón-electrón. Por lo tanto, podemos llamar al estado de energía más bajo el estado t 2g 2. Es equivalente al estado de los dos electrones que están en los orbitales t 2g. El segundo estado se llama estado t 2g e g. Es equivalente al estado de que un electrón esté en el t 2g y un electrón en los orbitales e g. El tercer estado se llama el estado e g 2, que es equivalente al estado con ambos electrones en los orbitales e g 2.
Reglas de selección
En la mayoría de los casos, la intensidad del campo del ligando está entre el caso muy débil y muy fuerte, y así, podríamos esperar espectros muy complicados. Afortunadamente, la naturaleza no hace las cosas tan complicadas, porque no todas las transiciones electrónicas posibles están permitidas cuantitativo-mecánicamente. Las transiciones permitidas están definidas por dos reglas: La regla de selección de giro y la regla Laporte.
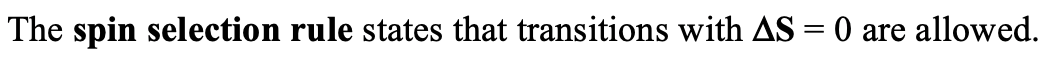
La regla de selección de espín establece que solo se permiten transiciones en las que el número cuántico de espín total S no cambia. Cuando S no cambia tampoco la multiplicidad de espín no cambia. Por lo tanto, las transiciones electrónicas solo se permiten para transiciones que no implican un cambio en la multiplicidad de espín. Por ejemplo, se permitiría excitar un electrón de un término de triplete a otro término de triplete, pero no de un término de triplete a un término de doblete o singlete.
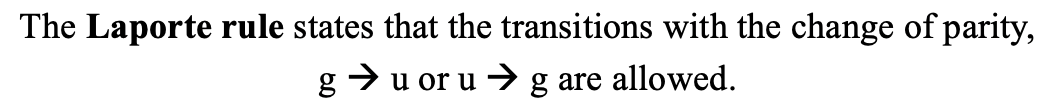
La regla de Laporte establece que las transiciones sólo se permiten cuando hay un cambio de paridad. Esto significa una transición de un gerade (g) a un término ungerado (u) y viceversa es posible, pero no una transición de un término g a otro término g, o la transición de un término u a otro término u. Por ejemplo, se permitiría la transición de un término T 2g a un T 1u, pero no la transición de un término T 2g a un T 1g.
Diagrama Tanabe-Sugano de un complejo octaédrico d 2
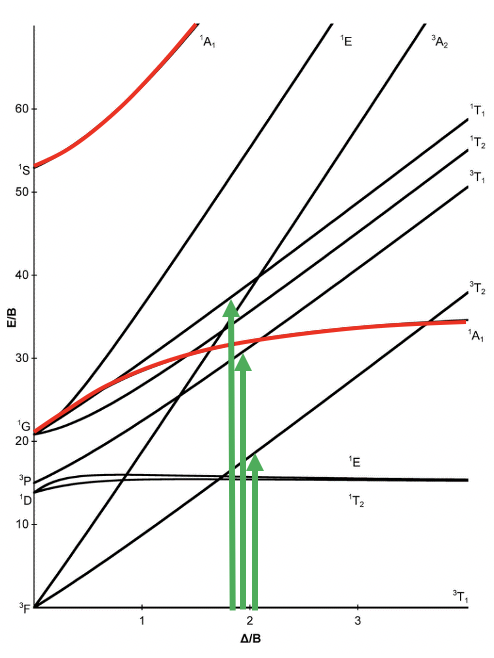
Un diagrama de correlación particular es el diagrama Tanabe-Sugano (Fig. 8.2.3). Se ilustra aquí para un complejo octaédrico d 2. La diferencia con el diagrama de correlación discutido anteriormente es que la energía del estado fundamental se traza horizontalmente, y la energía de todos los demás términos se grafica en relación con eso. En el caso de la configuración de electrones d 2, el término 3 T 1g es el término tierra y se traza como una línea horizontal. Podemos ver que la intensidad del campo del ligando en el eje x se da en unidades de B, y la energía de los términos también se da en unidades de B. B es un parámetro llamado Racah, es decir, una unidad de energía cuántico-mecánica para las interacciones electromagnéticas entre los electrones. Se elige porque proporciona números “prácticos”.
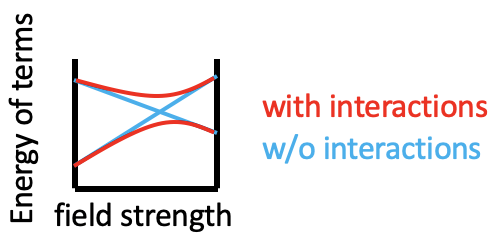
Se puede ver que algunas líneas en el diagrama están dobladas, y otras son rectas. La flexión de líneas ocurre cuando dos términos interactúan entre sí porque están cerca en energía y tienen la misma simetría. Esto vuelve a ser una analogía a los orbitales. Al igual que los orbitales interactúan cuando tienen el mismo tipo de simetría y energía similar, también los términos interactúan cuando tienen la misma simetría y la energía similar. Sin tomar en cuenta sus interacciones, sus energías pueden cruzar cuando la energía del término A disminuye y la energía del término B aumenta al aumentar la intensidad de campo (Fig. 8.2.4). Cuanto más se acercan los términos al punto en que se cruzan, más fuertes son sus interacciones, porque sus energías se vuelven cada vez más similares. Las interacciones llevan al hecho de que los términos “se doblan” entre sí, dando lugar a curvas dobladas. Esto significa que las curvas para dos términos del mismo tipo de simetría se doblarán en un diagrama de Tanabe-Sugano y nunca se cruzarán. Por ejemplo los términos para los dos términos de 1 A 1g se doblan uno del otro y no se cruzan.
A continuación, pensemos qué transiciones de electrones se permitirían bajo la consideración de la selección de espín y la regla de Laporte. Observamos que en los tipos de simetría se ha omitido la “g” para gerade (Fig. 8.2.3). Esta es una simplificación común que se hace en la literatura. Tenemos que recordarnos que todos los términos del diagrama son términos “g”. ¿Qué significa esto para la asignación de transiciones electrónicas? Significa que no se permitiría ninguna transición electrónica, y eso implicaría que el complejo no podría absorber la luz. Sin embargo, la regla de selección de Laporte no se sostiene estrictamente. Sólo dice que la probabilidad de la transición de electrones se reduce, sin embargo, no está prohibida. Esto significa que una banda de absorción que desobedece la regla de Laporte tendrá menor intensidad en comparación con una que sigue la regla de Laporte, pero aún se puede observar. La regla de selección de espín, sin embargo, se mantiene estrictamente, y las transiciones entre términos de diferente multiplicidad de espín están estrictamente prohibidas, lo que significa que tienen una probabilidad cercana a cero de ocurrir. En general, por lo tanto, podemos excitar un electrón del estado fundamental de 3 T 1 a otros términos de triplete, a saber, el término 3 T 2, y el término 3 A 2 (Fig. 8.2.3).
Diagrama Tanabe-Sugano de complejos octaédricos d 3
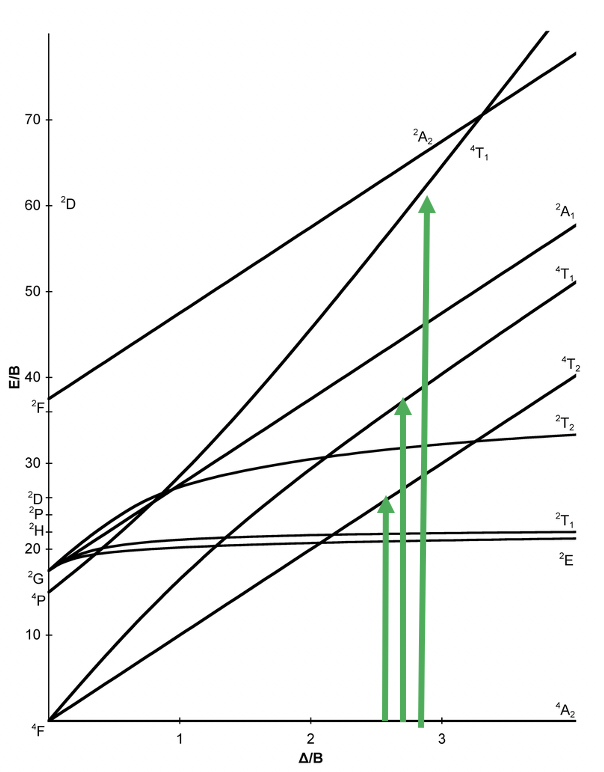
Ahora, echemos un vistazo al diagrama Tanabe-Sugano de un ion d 3 en un campo ligando octaédrico (Fig. 8.2.7). ¿Cuál es el término básico? Podemos ver el término designación en la línea horizontal dice “4 A 2”, por lo tanto este término es el término suelo. ¿Cuántas transiciones de electrones del estado fundamental debemos esperar? Para responder a esta pregunta necesitamos contar el número de otros términos del cuarteto. Ahí está el 4 T 2, el 4 T 1, y otro 4 T 1. Por lo tanto, en general hay tres transiciones de electrones posibles. ¿Podemos entender por qué el estado base es un término cuarteto?
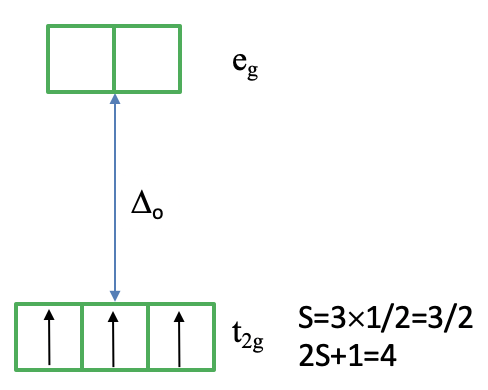
Ayuda a considerar cómo llenaríamos los electrones en los orbitales d para la configuración electrónica d 3. Los tres electrones se llenarían spin-up en el orbital t 2g siguiendo la regla de Hund (Fig. 8.2.8). Debido a que cada electrón tiene el espín +1/2, el espín total de los tres electrones es 3x1/2=3/2. Así, la multiplicidad de espín es ((3x3/2) +1) =4. Tenga en cuenta que el microestado que hemos dibujado es en realidad solo uno de los microestados (2L+1) (2S+1). S=3x1/2=3/2, pero ¿qué es L? Se puede ver uno el lado izquierdo del diagrama que el término 4 A 2 originó a partir de un término 4 F. Esto significa L=3, y (2L+1) ((2S+1) =7x4=28. Esto significa que en realidad hay otros 27 microestados que tienen la misma energía que el microestado que dibujamos. ¿Por qué dibujamos este microestado a favor de los demás? Esto se debe a que este microestado es el estado con los valores máximos M L (=L) y M s (=S) que determinan el término símbolo.
Diagrama Tanabe-Sugano de complejos octaédricos d 4
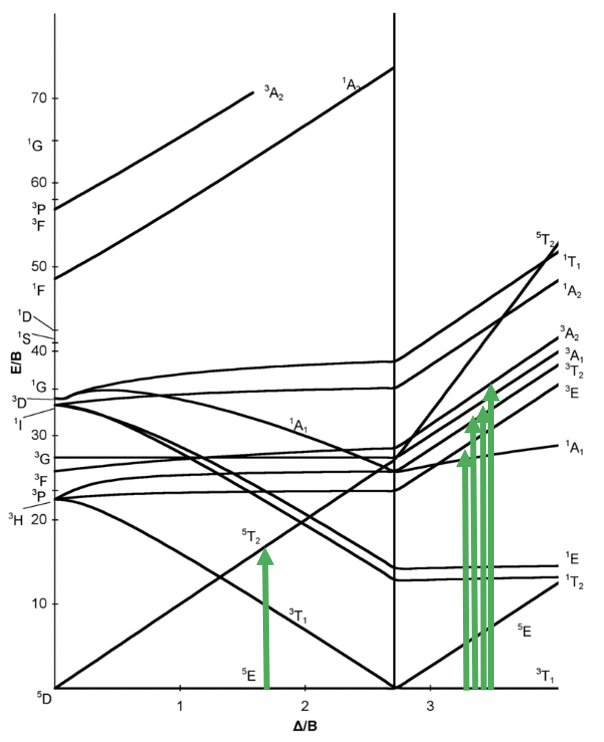
Ahora veamos el diagrama Tanabe-Sugano de un complejo octaédrico d 4. Se puede ver que este diagrama está separado en dos partes separadas por una línea vertical. La línea indica la intensidad del campo del ligando a la que el complejo cambia de un complejo de espín alto. A intensidades de campo de ligando más bajas, el término fundamental es un término de 5 E. A mayor intensidad de campo, el término suelo es un término de 3 T.
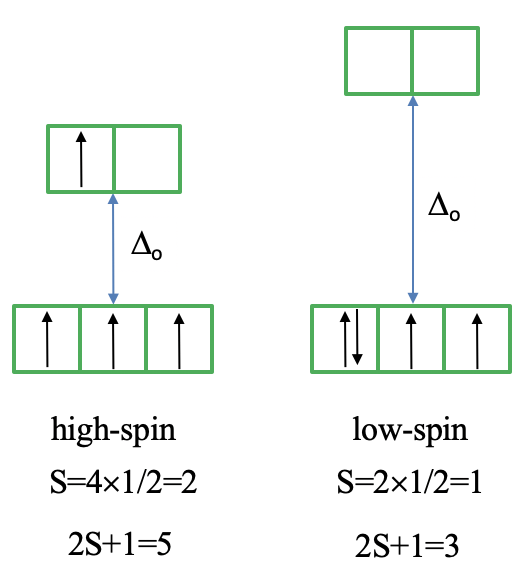
Podemos racionalizarlo nuevamente dibujando la representación de caja orbital de los orbitales d en el campo de ligandos octaédricos. En el estado de espín alto, hay cuatro electrones desapareados, así S=4x1/2=2, y 2S+1=5. En el estado de giro bajo, hay dos electrones desapareados, y así S=2x1/2=1, y 2S+1=3. Esto explica el quinteto y la naturaleza triplete de los términos de suelo de giro alto y bajo. Obsérvese nuevamente, que los dos microestados representados por los diagramas de caja orbital (Fig. 8.2.10) no son los únicos microestados que tienen la energía respectiva. Ellos son sólo los microestados “representativos” porque los tienen los valores máximos de M L y M S.
¿Cuántas transiciones de electrones son posibles a partir del término tierra? Para un complejo de alto giro solo hay uno porque el es solo otro término de quinteto, es decir, el término 5 T 2. Para el complejo de giro bajo, hay cinco transiciones porque hay otros cinco términos de triplete.
Diagrama Tananbe-Sugano de complejos octaédricos d 5
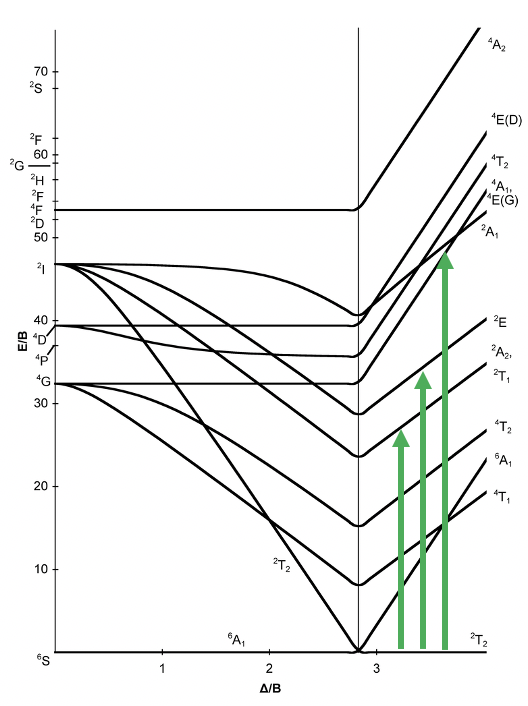
También el diagrama Tanabe-Sugano de un complejo octaédrico d 5 se divide en dos partes separadas por una línea vertical (Fig. 8.2.11). La parte izquierda refleja el giro alto y la parte derecha el complejo de giro bajo.
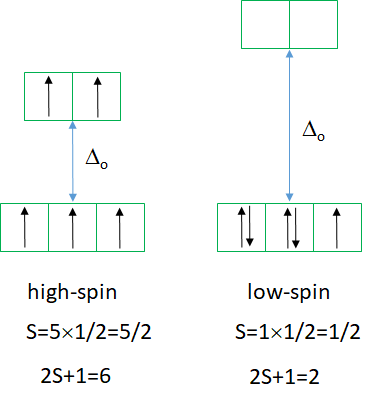
El estado fundamental de giro alto es un término sexteto, y el estado fundamental de giro bajo es un término doblete. Podemos entender la naturaleza de sexteto y doblete de los términos al considerar que el diagrama de caja de electrones asociado tiene cinco y uno electrones desapareados respectivamente. S=5x1/2=5/2 y 2S+1=6 para el término de espín alto, y S=1x1/2=1/2 y 2S+1=2 para el término de giro bajo. ¿Cuáles son las posibles transiciones de electrones desde el estado fundamental? Para el complejo de alto espín no existe otro término sexteto, lo que significa que no hay transición electrónica posible. De ahí que los complejos d5 octaédricos de alto espín sean incoloros. Un ejemplo es el complejo hexaaqua manganeso (2+). Una solución de este complejo es casi incolora, sólo muy ligeramente rosada. El ligero color se debe a que también pueden ocurrir transiciones prohibidas por giro, aunque con una probabilidad muy baja. Para un complejo d 5 -bajo espín hay tres estados de doblete adicionales, y por lo tanto hay tres transiciones de electrones posibles.
Diagrama Tanabe-Sugano de complejos octaédricos d 6
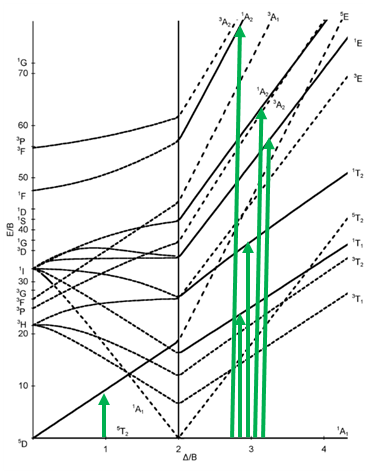
El siguiente diagrama es el de la configuración de electrones d 6 (Fig. 8.2.13). Nuevamente, el diagrama se separa en partes para complejos de espín alto y bajo. Se pueden ver líneas punteadas en el diagrama. Indican los términos que tienen una multiplicidad de espín diferente a la del término suelo. De esta manera podemos ver más fácilmente cuántas transiciones de electrones están permitidas.
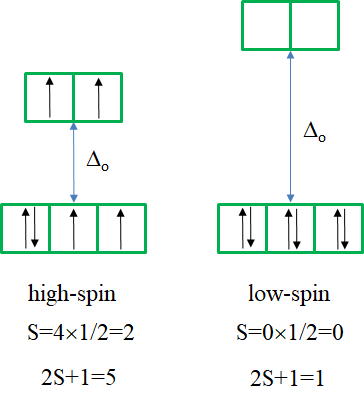
El término suelo para el complejo de alto espín es el término quinteto 5 T 2. Es un término de quinteto porque cuatro electrones en los orbitales d están desapareados, y dos están emparejados. El valor para S es así 4x1/2=2, y la multiplicidad de espín es 2S+1=5. El término suelo para el complejo de bajo espín es un término de 1 A 1. Es un término singlete porque todos los electrones están emparejados, y así S=0, y 2S+1=1. ¿Cuántas transiciones de electrones hay para el complejo de alto espín? Sólo hay uno porque el término 5 E es el único otro término de quinteto. Hay cinco transiciones posibles para el caso de giro bajo porque hay cinco términos singlete adicionales.
Diagrama Tanabe-Sugano de complejos octaédricos d 7
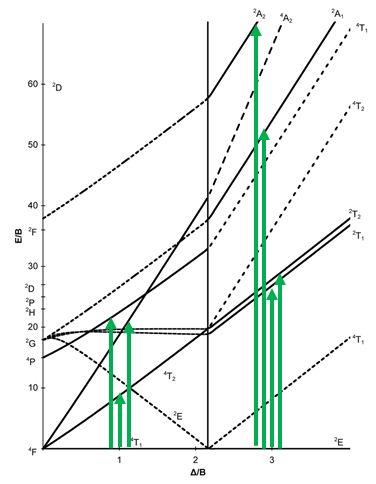
A continuación, veamos el diagrama Tanabe-Sugano de un complejo octaédrico d 7 (Fig. 8.2.15). En este caso, el complejo de alto giro tiene un término de suelo de 4 T 1, y el complejo de giro bajo tiene un término de suelo de 2 E.
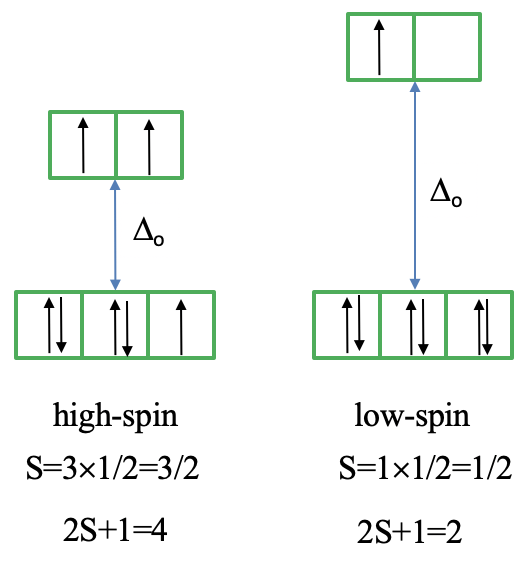
El microestado que “representa” el término de tierra de espín alto tiene tres electrones desapareados, de ahí el número cuántico de espín S=3/2 y la multiplicidad de espín es 2S+1 = 4. El microestado que representa el término de tierra de espín bajo tiene un electrón desapareado, un valor S de ½ y una multiplicidad de espín de 2. Hay otros tres términos de cuarteto, y otros cuatro términos dobletes, de ahí que haya tres transiciones de electrones para el complejo de alto espín y cuatro para el complejo de espín bajo.
Diagrama Tanabe-Sugano de complejos octaédricos d 8
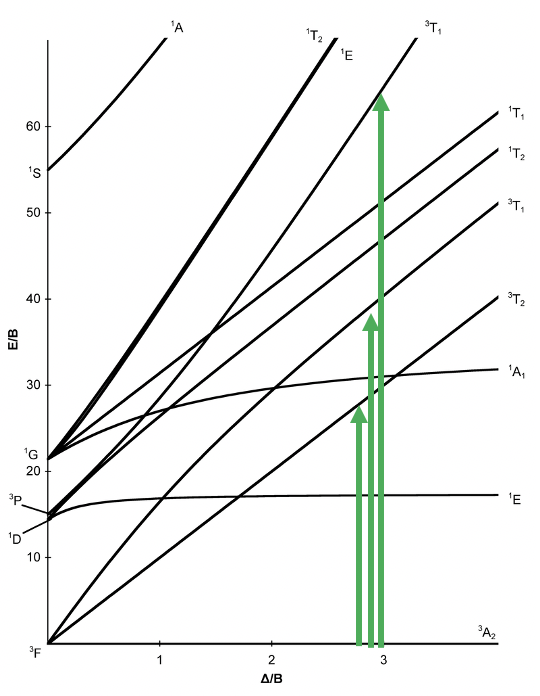
Ahora veamos un complejo octaédrico con configuración de electrones d 8. Para esta configuración electrónica, no hay complejos de espín alto y bajo posibles, por lo tanto, el diagrama Tanabe-Sugano ya no se divide en dos partes (Fig. 8.2.17).
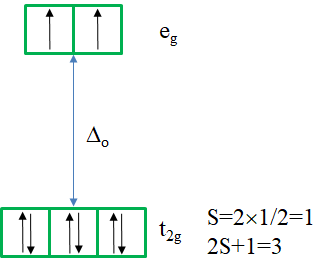
Hay un término de suelo único del tipo 3 A 2. Es un estado triplete porque el microestado que representa el término tiene dos electrones desapareados en los orbitales e g (Fig. 8.2.18). Así, S=2x1/2=1, y la multiplicidad de espín es 2S+1=2. ¿Cuántas transiciones de electrones esperarías? Hay otros tres estados tripletes, a saber, los términos 3 T 2 y dos 3 T 1. Por lo tanto, hay tres transiciones de electrones posibles.
También podríamos preguntar: ¿Hay diagramas Tanabe-Sugano para d 1, d 9, y d 10? Porque, d 1 no hay interacciones electrón-electrón, por lo que la imagen orbital simple es suficiente. El término 2 D se divide en términos T 2g y E g, y solo hay una transición electrónica posible. La configuración de electrones d 9 es el “análogo de agujero” de la configuración de electrones d 1. También tiene solo un término 2 D que se divide en un término T 2g y un término E g en el campo ligando octaédrico. Por lo tanto, también en este caso solo hay una transición electrónica del término T 2g al término E g posible. En el caso del d 10 todos los microestados están llenos de orbitales, y solo existe el término 1 S que no se divide en un campo de ligando octaédrico. Por lo tanto, no hay transiciones de electrones en este caso.
Por último, cabe mencionar que también es posible construir diagramas Tanabe-Sugano para otras formas como la forma tetraédrica, pero no los discutiremos más aquí.
Transiciones de transferencia de

Todavía no hemos terminado con nuestros espectros electrónicos. Por lo tanto, hasta ahora solo hemos considerado transiciones de electrones d entre d-orbitales, y sus términos. Se llaman transiciones d-d. Sin embargo, también existen las llamadas transiciones de transferencia de carga posibles, que no son transiciones d-d. Podemos ver fácilmente que debe haber otras transiciones pero transiciones d-d cuando miramos el color de los iones d 10 y d 0. Para aquellos, las transiciones no son posibles d-d. Por lo tanto, todos deben ser incoloros. Sin embargo, eso no siempre es cierto. Algunos de estos iones son efectivamente incoloros, pero otros no (Fig. 8.2.19). Por ejemplo, Zn 2 +, un ion d 10 es incoloro en complejos, pero no Cu (I) que también es d 10. Mientras que el tetraquis (acetonitrilo) cobre (+) es incoloro, el bis (fenantreno) cobre (+) es de color naranja oscuro. Similar es cierto para los iones d 0. Mientras que TiF 4 y TiCl 4 son incoloros, TiBr 4 es naranja y TiI 4 es marrón. Algunas especies d 0 son incluso extremadamente coloridas, por ejemplo permanganato con Mn 7 + que es extremadamente púrpura, y dicromato con Cr (VI) que es naranja brillante.
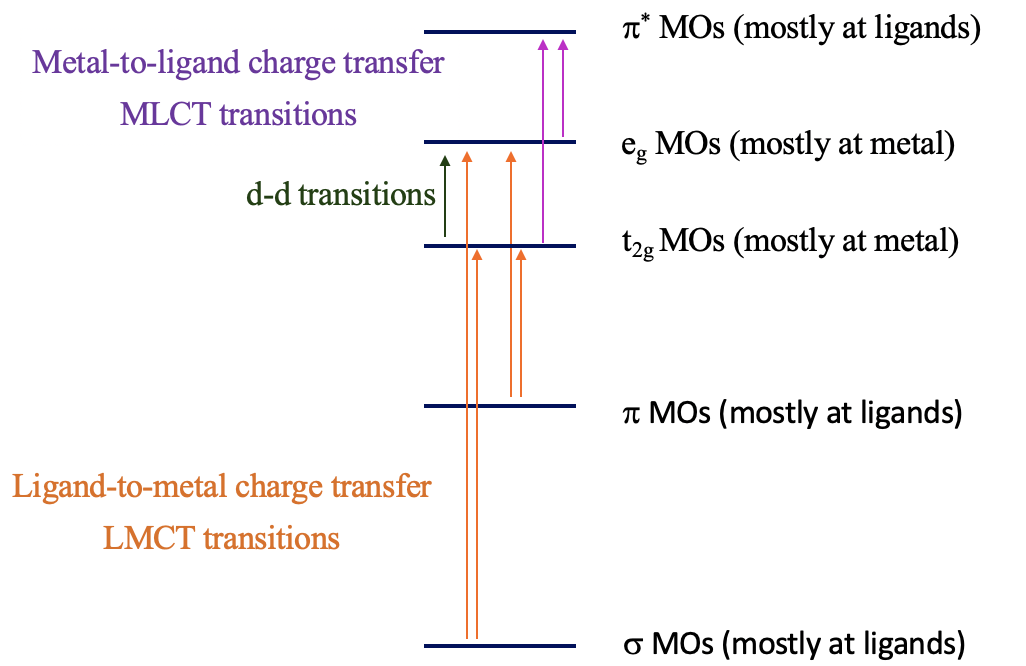
La explicación de estos fenómenos son las transiciones de carga-transferencia (Fig. 8.2.20). Hay dos tipos de transiciones de transferencia de carga, la transición de transferencia de carga ligando-metal (LMCT) y la transición de transferencia de carga de metal a ligando (MLCT). Para las transiciones ligando-metal, los electrones de la unión σ y π-orbitales se excitan en orbitales d metálicos en el campo ligando, por ejemplo los orbitales t 2g y e g en un complejo octaédrico. Si la diferencia de energía entre los orbitales σ/π-y los orbitales d es lo suficientemente pequeña, entonces esta transición de electrones se asocia con la absorción de luz visible. La transición se denomina transición ligando a metal porque los orbitales σ/π-ligando se localizan principalmente en los ligandos, mientras que los orbitales metal-d-en un campo de ligando se localizan principalmente en el metal. Viceversa, la transición de metal a ligando implica la transición de un electrón de orbitales d metálicos en un campo de ligando a orbitales π*-ligando. Esto esencialmente mueve la densidad electrónica del metal al ligando, de ahí el nombre de transición de transferencia de carga de ligando a metal. Si la diferencia de energía entre el ligando π* y los orbitales metálicos es lo suficientemente pequeña, entonces la absorción ocurre en el rango visible. Las transiciones de transferencia de carga suelen ser permitidas tanto en espín como en Laporte, de ahí que si ocurren el color suele ser muy intenso. ¿Cómo podemos distinguir entre d-d y transiciones de transferencia de carga? Las transiciones de transferencia de carga a menudo cambian de energía a medida que la polaridad del disolvente varía (solvatocrómica) ya que hay un cambio en la polaridad del complejo asociado con la transición de transferencia de carga. Esto se puede utilizar para distinguir entre transiciones d-d y bandas de transferencia de carga.
Transiciones LMCT
¿Podemos predecir cuándo las ventanas de energía entre los orbitales moleculares de unión y los orbitales d metálicos son lo suficientemente pequeñas para que las transiciones LMCT en lo visible puedan tener lugar? Generalmente, sería deseable que la energía de los orbitales metálicos fuera lo más baja posible y la energía de los orbitales del ligando de unión sea lo más alta posible. La energía de los d-orbitales metálicos disminuye al aumentar la carga positiva en el metal debido a que aumenta la carga nuclear efectiva sobre el metal. Esto significa que los estados de oxidación de metales muy altos favorecen una transición LMCT. Los orbitales d deben tener pocos o ningún electrón, de modo que los electrones puedan ser promovidos hacia los orbitales, y la energía orbital disminuye debido a que se minimiza la repulsión electrón-electrón. Ejemplos son Mn (VII), Cr (VI) y Ti (IV). La energía de los MO de los orbitales ligantes de unión aumenta cuando los orbitales del ligando tienen alta energía, lo que suele ser el caso para el ligando donador π con carga negativa (Fig. 8.2.21).


Ejemplos de ligandos son ligandos oxo y halo. Esto explica por ejemplo las transiciones LMCT en permanganato. El Mn está en el estado de oxidación muy alto +7, y los ligandos son oxo-ligandos que son donadores π con una carga 2- negativa. Las transiciones son tanto Laporte como spin-permitido dando lugar a una intensidad muy alta de absorción de luz, y por lo tanto color (Fig. 8.2.21).
Transiciones MLCT
Entonces, ¿cuáles son las propiedades favorables del ion metálico y del ligando para una transición de metal a ligando? En este caso nos gustaría mantener la energía de los orbitales metálicos lo más alta posible para que se minimice la diferencia de energía entre un d-orbital metálico y un orbital π*-orbital. Esto se logra cuando la carga positiva en el ion metálico es pequeña, y hay muchos electrones d que pueden repelerse entre sí, aumentando así las energías orbitales, por ejemplo Cu (I), Fig. 8.2.22.
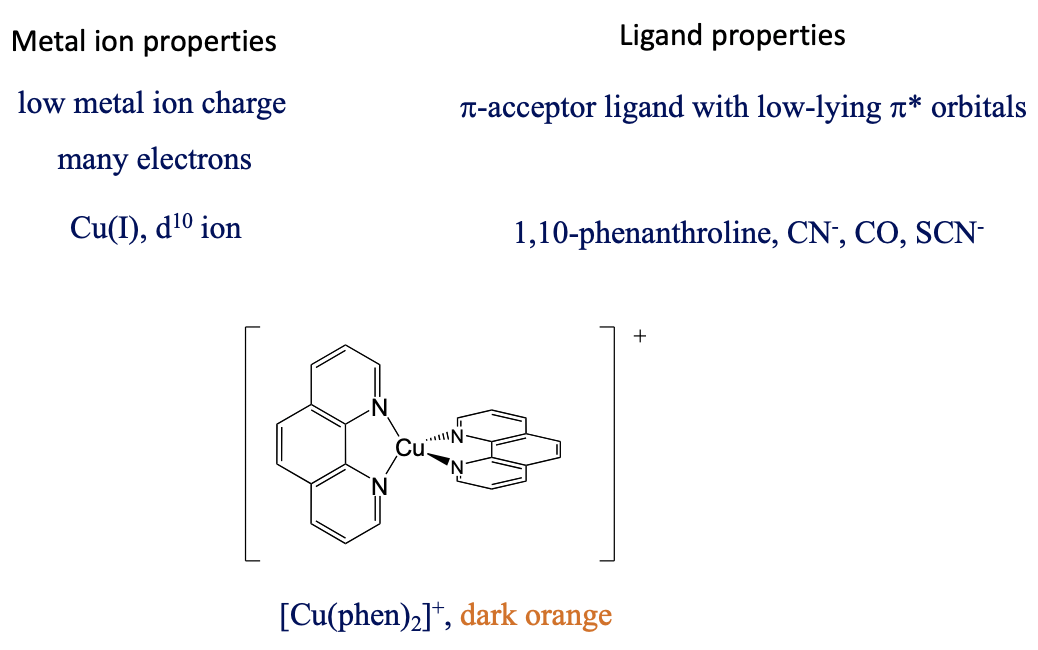
El ligando debe ser un aceptor π con orbitales π*-bajos, por ejemplo fenantrolina, CN -, SCN - y CO. Por ejemplo, el bis (fenantrolina) cobre (+) es de color naranja oscuro y tiene una banda de absorción MLCT a 458 nm. Además, la transferencia MLCT está permitida tanto por giro como en Laporte.
Cabe mencionar que algunos complejos permiten transiciones tanto de metal a ligando como de ligando a metal. Por ejemplo, en el complejo Cr (CO) 6 los orbitales σ-orbitales son lo suficientemente altos y los orbitales π*-son lo suficientemente bajos en energía para permitir la absorción de luz en el rango visible. Finalmente, también son posibles bandas intraligand cuando el ligando es un cromóforo.


