8.2: Radiactividad
- Page ID
- 77363
La causa de la radiactividad
Solo una combinación particular de protones y neutrones forma nucleoides estables; el resto son nucleoides inestables, como se ilustra en la Fig. 8.2.1. Las observaciones sobre los nucleoides estables son las siguientes.
- El hidrógeno con un protón y sin neutrones es un nucleoide estable.
- Otros nucleoides ligeros, hasta el número atómico 20 suelen ser estables cuando el número de protones es igual al número de neutrones
- Los nucleoides medios de los números atómicos del 20 al 82 son generalmente estables cuando el número de neutrones es mayor que el número de protones.
- Los nucleoides más pesados con número atómico 84 o más son inestables.
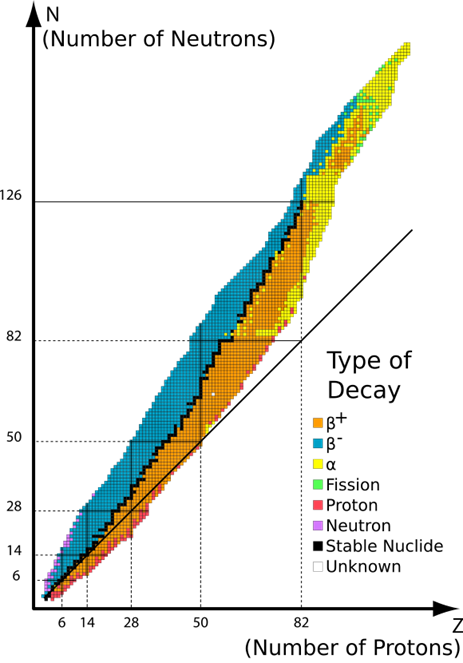
Los nucleoides mostrados como puntos negros en la Fig. 8.2.1 son nucleoides estables de origen natural. Todos los nucleoides mostrados en puntos coloreados distintos del negro son inestables.
Los nucleoides inestables son radiactivos, se desintegran espontáneamente, es decir, tienden a reorganizar la composición del nucleón en el núcleo para convertirse en un nucleoide más estable.
La radiactividad libera energía y partículas, es decir, radiación nuclear junto con el reordenamiento del núcleo, como se explica en los siguientes apartados.
Desintegración alfa
La\(\ce{\alpha}\) emisión es uno de los procesos importantes para estabilizar los nucleoides pesados inestables que se muestran con puntos amarillos en la Fig. 8.2.1. Dado que la\(\ce{\alpha}\) partícula -tiene dos protones y dos neutrones, el nucleoide hijo producido junto con la\(\ce{\alpha}\) desintegración tiene dos protones menos y cuatro números de masa menos en ella que el nucleoide parental, como se ilustra en la Fig. 8.2.2.

Por ejemplo:
\[\ce{_92^238U -> _90^234Th + _2^4He}\nonumber\]
Algunas veces la\(\ce{\alpha}\) -decaimiento va acompañada de\(\ce{\gamma}\) -emisión, por ejemplo:
\[\ce{_84^210Po -> _82^206Pb + _2^4He + \gamma}\nonumber\]
Tenga en cuenta que los\(\ce{\gamma}\) rayos -tienen masa cero, por lo que no cambian el número atómico y el número másico del nucleoide padre.
- Escribe los símbolos de los nucleoides, partículas y radiaciones conocidos en los reactivos y productos, separados por una flecha. Deja un signo de interrogación para los datos desconocidos.
- Equilibrar el número de masa en los dos lados de la ecuación.
- Equilibrar el número atómico en los dos lados de la ecuación.
- Wright los símbolos del nucleoide desconocido o partículas encontrándolos en la tabla periódica, con base en los números atómicos.
Los detectores de humo utilizados en los hogares necesitan\(\ce{\alpha}\) -partículas para su función. Americio-241 es el\(\ce{\alpha}\) -emisor de descomposición utilizado en los detectores de humo.
Escribir la ecuación de reacción nuclear para la\(\ce{\alpha}\) -decaimiento del americio-241.
Solución
Paso 1. El símbolo y el número atómico de americio en la tabla periódica son Am y 95, respectivamente. Entonces la ecuación inicial es:
\[\ce{_95^241Am -> _{?}^{?}{?} + _2^4He}\nonumber\]
Paso 2. Equilibrar el número de masa en los dos lados de la ecuación, es decir, el número de masa del nucleoide desconocido es 241-4 = 237:
\[\ce{_95^241Am -> _{?}^{237}{?} + _2^4He}\nonumber\]
Paso 3. Equilibrar el número atómico en los dos lados de la ecuación, es decir, el número atómico del nucleoide desconocido es 95-2 = 93:
\[\ce{_95^241Am -> _{93}^{237}{?} + _2^4He}\nonumber\]
Paso 4. Encuentra el símbolo del nucleoide desconocido de la tabla periódica de elementos, es decir, el elemento en el número atómico 93 es el símbolo de neptunio Np:
\[\ce{_95^241Am -> _{93}^{237}{Np} + _2^4He}\nonumber\]
Esta es la ecuación nuclear equilibrada para la\(\ce{\alpha}\) -decaimiento del americio-241 en los detectores de humo.
El radio-226, presente en muchos tipos de rocas y suelos, es un\(\ce{\alpha}\) emisor que produce radón-226 en el proceso. El radón-226 también es un\(\ce{\alpha}\) -emisor que puede difundirse en las casas desde las rocas y el suelo debajo de los edificios. El radón es un problema de salud ambiental en los edificios cuando su concentración se vuelve por encima de cierto nivel. La ecuación nuclear para la\(\ce{\alpha}\) -desintegración del radón-222 es la siguiente.
\[\ce{_86^222Rn -> _{84}^{218}{Po} + _2^4He}\nonumber\]
Escriba la ecuación nuclear para la desintegración α del radio-226.
Solución
Paso 1. La ecuación inicial es:
\[\ce{_88^226Rn -> _{?}^{?}{?} + _2^4He}\nonumber\]
Paso 2. Equilibrar el número de masa en los dos lados de la ecuación, es decir, es 226-4 = 222:
\[\ce{_88^226Rn -> _{?}^{222}{?} + _2^4He}\nonumber\]
Paso 3. Equilibrar el número atómico en los dos lados de la ecuación, es decir, 88-2 = 86:
\[\ce{_88^226Rn -> _{86?}^{222}{?} + _2^4He}\nonumber\]
Paso 4. Encuentra el símbolo del nucleoide desconocido de la tabla periódica de elementos, es decir, el elemento en el número atómico 86 es el símbolo de radón Rn:
\[\ce{_88^226Rn -> _{?}^{222}{Rn} + _2^4He}\nonumber\]
Esta es la ecuación nuclear equilibrada para la\(\ce{\alpha}\) -desintegración del radio-226 en rocas y suelo.
Decaimiento beta
Los nucleoides marcados con azul en la Fig. 8.2.1. tienen más neutrones de los necesarios para la estabilidad. Suelen estabilizarlos convirtiendo uno de los neutrones (n) en un protón (p) y un electrón (e) mediante el siguiente proceso nuclear:
\[\ce{_{0}^{1}{n} -> _{1}^{1}{p} + _{-1}^{0}{e}}\nonumber\]
El protón permanece en el núcleo, pero el electrón emite desde el núcleo, como se ilustra en la Fig. 8.2.3. El electrón emitido se llama\(\ce{\beta}\) -partícula. El proceso de emisión\(\ce{\beta}\) de partículas se llama beta-decaimiento. Tenga en cuenta que el neutrón tiene número atómico cero ya que no hay protón en él, y el electrón tiene un número atómico -1 para equilibrar el número atómico +1 del protón. El protón tiene +1 y el electrón tiene -1 carga, que también está balanceada. El número de masa de un electrón es cero ya que tiene una masa insignificante en comparación con la masa de un protón o un neutrón. En esta ecuación se ignoran las cargas eléctricas y la emisión de otra partícula llamada neutrino.
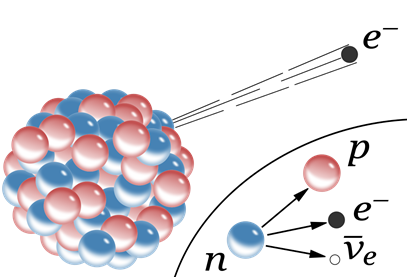
Un ejemplo de desintegración β es la transformación de nitrógeno-16 a oxígeno-17:
\[\ce{_{7}^{16}{N} -> _{8}^{16}{O} + _{-1}^{0}{e}}\nonumber\]
Tenga en cuenta que en el proceso\(\ce{\beta}\) -decaimiento, el número de masa sigue siendo el mismo, pero el número atómico aumenta en uno en el núcleo hijo. La ecuación nuclear se equilibra porque el número de masa es el mismo (16 = 16+0), y el número atómico también es el mismo (7 = 8-1) en los dos lados de la ecuación.
El yodo-131 se utiliza para la radioterapia de una glándula tiroides hiperactiva.
El ittrio-90 se usa para tratar el cáncer y también se inyecta en las articulaciones grandes para aliviar el dolor debido a la artritis.
Phosphorous-32 se utiliza para tratar la leucemia y otros trastornos de la sangre.
El carbono-14 se utiliza para determinar la edad de un fósil o de un objeto antiguo.
Escribir la ecuación nuclear para la\(\ce{\beta}\) -decadencia del yodo-131.
Solución
Paso 1. El símbolo y el número atómico de yodo en la tabla periódica son I y 53, respectivamente. Entonces la ecuación inicial es:
\[\ce{_{53}^{131}{I} -> _{?}^{?}{?} + _{-1}^{0}{e}}\nonumber\]
Paso 2. Equilibrar el número de masa en los dos lados de la ecuación, es decir, el número de masa del nucleoide desconocido es 131-0 = 131:\[\ce{_{53}^{131}{I} -> _{?}^{131}{?} + _{-1}^{0}{e}}\nonumber\]
Paso 3. Equilibrar el número atómico en los dos lados de la ecuación, es decir, el número atómico del nucleoide desconocido es 53- (-1) = 54:\[\ce{_{53}^{131}{I} -> _{54}^{131}{?} + _{-1}^{0}{e}}\nonumber\]
Paso 4. Encuentra el símbolo del nucleoide desconocido de la tabla periódica de elementos, es decir, el elemento en el número atómico 54 es el símbolo de xenón Xe:
\[\ce{_{53}^{131}{I} -> _{54}^{131}{Xe} + _{-1}^{0}{e}}\nonumber\]
Esta es la ecuación nuclear equilibrada para la desintegración α del yodo-131 que se usa para tratar las glándulas tiroideas hiperactivas.
Escriba la ecuación nuclear para la desintegración β del itrio-90.
Solución
Paso 1. El símbolo y el número atómico de itrio en la tabla periódica son Y y 39, respectivamente. Entonces la ecuación inicial es:
\[\ce{_{39}^{90}{Y} -> _{?}^{?}{?} + _{-1}^{0}{e}}\nonumber\]
Paso 2. Equilibrar el número de masa en los dos lados de la ecuación, es decir, el número de masa del nucleoide desconocido es 90-0 = 90:
\[\ce{_{39}^{90}{Y} -> _{?}^{90}{?} + _{-1}^{0}{e}}\nonumber\]
Paso 3. Equilibrar el número atómico en los dos lados de la ecuación, es decir, el número atómico del nucleoide desconocido es 39- (-1) = 40:
\[\ce{_{39}^{90}{Y} -> _{40}^{90}{?} + _{-1}^{0}{e}}\nonumber\]
Paso 4. Encuentra el símbolo del nucleoide desconocido de la tabla periódica de elementos, es decir, el elemento en el número atómico 40 es el símbolo de circonio Z:
\[\ce{_{39}^{90}{Y} -> _{40}^{90}{Z} + _{-1}^{0}{e}}\nonumber\]
Esta es la ecuación nuclear equilibrada para la desintegración β del itrio-90.
Emisión de positrones
Los nucleoides marcados con naranja en la Fig. 8.2.1. tienen más protones de los necesarios para la estabilidad. Suelen estabilizarlos convirtiendo uno de los protones (p) en un neutrón (n) y un positrón\(\ce{\beta^+}\) mediante el siguiente proceso nuclear:
\[\ce{_{1}^{1}{p} -> _{0}^{1}{n} + _{1}^{0}{e}}\nonumber\]
El neutrón permanece en el núcleo, pero el positrón emite desde el núcleo, como se ilustra en la Fig. 8.2.4. Tenga en cuenta que el positrón tiene un número de masa +1 que equilibra el número atómico +1 del protón en el otro lado de la ecuación. El positrón tiene una carga +1 que también equilibra la carga +1 del protón en el otro lado de la ecuación. El número de masa de un positrón es cero ya que tiene una masa insignificante en comparación con la masa de un protón o un neutrón. Las cargas eléctricas no se muestran en la ecuación nuclear.
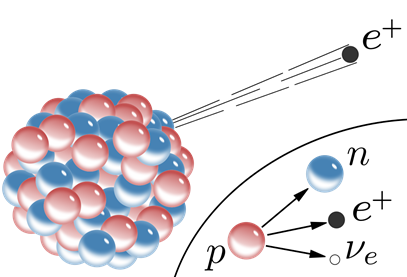
Carbon-11 es un ejemplo de positrón-emisor:
\[\ce{_{6}^{11}{I} -> _{5}^{11}{B} + _{1}^{0}{e}}\nonumber\]
Tenga en cuenta que en el proceso de emisión de positrones, el número de masa sigue siendo el mismo, pero el número atómico disminuye en uno en el núcleo hijo. La ecuación nuclear se equilibra porque el número de masa es el mismo (11 = 11+0), y el número atómico también es el mismo (7 = 5+1) en los dos lados de la ecuación.
La emisión de positrones se utiliza en la tomografía por emisión de positrones (PET) que es una técnica de imagen médica. Los isótopos emisores de positrones de corta duración 11 C, 13 N, 15 O y 18 F utilizados para la tomografía por emisión de positrones se producen típicamente por irradiación de protones de dianas naturales o enriquecidas descritas en una sección posterior.
El fluor-18 en la fluorodesoxiglucosa, abreviado como [18 F] FDG es un emisor de positrones comúnmente utilizado para detectar cáncer, y en [18 F] NaF es ampliamente utilizado para detectar la formación ósea. Otros ejemplos son el oxígeno-15 en [15 O] H 2 O utilizado para medir el flujo sanguíneo y el nitrógeno-13 utilizado para etiquetar moléculas de amoníaco para imágenes de perfusión miocárdica.
\[\ce{_{8}^{15}{O} -> _{7}^{15}{N} + _{1}^{0}{e}}\nonumber\]
\[\ce{_{7}^{13}{N} -> _{6}^{13}{C} + _{1}^{0}{e}}\nonumber\]
Escribir la ecuación nuclear para la emisión de positrones de fluor-18?
Solución
Paso 1. El símbolo y el número atómico de flúor en la tabla periódica son F y 9, respectivamente. Entonces la ecuación inicial es:
\[\ce{_{9}^{18}{F} -> _{?}^{?}{?} + _{1}^{0}{e}}\nonumber\]
Paso 2. Equilibrar el número de masa en los dos lados de la ecuación, es decir, el número de masa del nucleoide desconocido es 18-0 = 131:\[\ce{_{9}^{18}{F} -> _{?}^{131}{?} + _{1}^{0}{e}}\nonumber\]
Paso 3. Equilibrar el número atómico en los dos lados de la ecuación, es decir, el número atómico del nucleoide desconocido es 9- (+1) = 8:
\[\ce{_{9}^{18}{F} -> _{8}^{131}{?} + _{1}^{0}{e}}\nonumber\]
Paso 4. Encuentra el símbolo del nucleoide desconocido de la tabla periódica de elementos, es decir, el elemento en el número atómico 8 es el símbolo de oxígeno O:
\[\ce{_{9}^{18}{F} -> _{8}^{18}{?} + _{1}^{0}{e}}\nonumber\]
Esta es la ecuación nuclear equilibrada para la emisión de positrones de fluor-18.
Emisión gamma
Los rayos gamma son radiaciones electromagnéticas de alta energía que no tienen masa ni carga. Entonces, la\(\ce{\gamma}\) emisión pura ocurre desde el núcleo, pero no resulta en transmutación, simplemente el nucleoide cambia de un estado más inestable, llamado estado metaestable, a un estado relativamente estable, como se ilustra en la Fig. 8.2.5.
Un símbolo m o * junto al número de masa como superíndice a la derecha indica el estado metaestable del nucleoide parental. Por ejemplo, el tecnecio-99m es un\(\ce{\gamma}\) -emisor ampliamente utilizado en imágenes médicas:
\[\ce{_{43}^{99m}{Tc} -> _{43}^{199}{Tc } + \gamma}\nonumber\]
Del mismo modo, boro-11m es un\(\ce{\gamma}\) -emisor:
\[\ce{_{5}^{11m}{B} -> _{5}^{11}{B } + \gamma}\nonumber\]
Obsérvese que el nucleoide permanece igual después de\(\ce{\gamma}\) -emisión, excepto por el cambio de forma metaestable a un estado más estable indicado por m.
A menudo, la\(\ce{\gamma}\) -emisión acompaña a\(\ce{\alpha}\) -emisión o\(\ce{\beta}\) -emisión. Por ejemplo, el polonio-210 decae por una\(\ce{\alpha}\) emisión y\(\ce{\gamma}\) -emisiones simultáneas.
\[\ce{_{84}^{210}{Po} -> _{82}^{206}{Pb } + _2^4He + \gamma}\nonumber\]
De igual manera, el iridio-192 se utiliza en implantes para tratar el cáncer de mama, y el cobalto-60 utilizado como fuente de radiación externa para el tratamiento del cáncer, emiten\(\ce{\beta}\) y\(\ce{\gamma}\) -rayos simultáneamente.
\[\ce{_{77}^{192}{Ir} -> _{78}^{192}{Pt } + _{-1}^{0}{e} + \gamma}\nonumber\]
\[\ce{_{27}^{60}{Co} -> _{28}^{60}{Ni } + _{-1}^{0}{e} + \gamma}\nonumber\]
El yodo-131 se descompone en\(\ce{\beta}\) -partícula y xenón-131m que es seguido rápidamente por un\(\ce{\gamma}\) -decaimiento de xenón-131m.
\[\ce{_{53}^{131}{I} -> _{54}^{131m}{Xe } + _{-1}^{0}{e}}\nonumber\]
\[\ce{_{54}^{131m}{Xe} -> _{54}^{131}{Xe} + \gamma}\nonumber\]
Formas menos comunes de radiactividad
Se conocen varias formas relativamente menos comunes de radiactividad. Algunos ejemplos son los siguientes.
- La emisión de neutrones es un modo de desintegración radiactiva en el que uno o más neutrones son expulsados de un núcleo.
- La emisión de protones es una forma rara de radiactividad en la que un protón emite desde un nucleoide.
- La fisión espontánea es un proceso radiactivo en el que un nucleoide más masivo se rompe en nucleoides más pequeños, a menudo junto con la emisión de partículas nucleares más pequeñas.
- En la captura de electrones, se captura un electrón externo para reaccionar con protones y producir un neutrón en el núcleo.
Por ejemplo, el berilio-7 decae por captura de electrones, como se muestra en la siguiente ecuación.
\[\ce{_{4}^{7}{Be} + _{-1}^{0}{e} -> _{3}^{7}{Li} + \gamma}\nonumber\]
Tenga en cuenta que el número de masa sigue siendo el mismo, pero el número atómico disminuye en uno en el proceso de captura de electrones.
El cromo-51, que se utiliza para la obtención de imágenes del bazo, se descompone por la captura y\(\ce{\gamma}\) emisión de electrones.
\[\ce{_{24}^{51}{Cr} + _{-1}^{0}{e} -> _{23}^{51}{V} + \gamma}\nonumber\]
Resumen del modo de desintegración de los nucleoides radiactivos
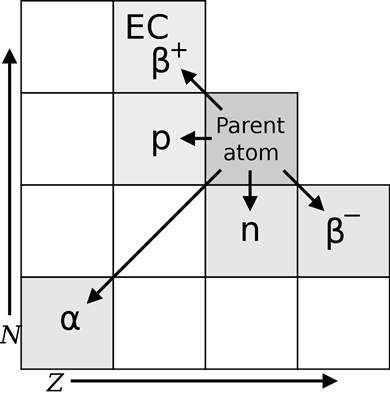
La Fig. 8.2.6 resume los cambios en la composición nucleoide tras diferentes eventos radiactivos descritos anteriormente.