8.4: Mediciones de radiación
- Page ID
- 77365
Medición de radiactividad
La radiactividad se mide en términos de la tasa de eventos radiactivos. Las radiaciones nucleares son radiaciones ionizantes, es decir, derriban electrones de átomos o moléculas que se interponen en su camino, dejando atrás cationes. El contador Geiger Muller es uno de los instrumentos de medición de radiaciones que cuenta la desintegración del radionucleótido por segundo al registrar la corriente producida por la acción de ionización de la radiación, como se ilustra en la Fig. 8.4.1. No es solo un evento de ionización; la partícula nuclear sigue ionizando los átomos en su trayectoria hasta que se agota su energía, como se ilustra en la Fig. 8.4.2. El instrumento registra el destello de la corriente eléctrica producida por la ionización de cada desintegración radiactiva.
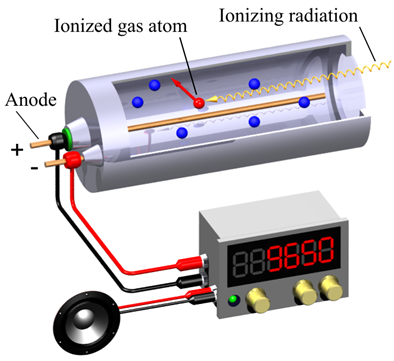

La unidad de radiactividad SI es Becquerel (Bq), es decir, el número de núcleos que se desintegran por segundo.
La unidad común de intensidad de radiación es Curie (Ci), es decir, 3.7 x 10 10 desintegraciones por segundo. La relación entre Becquerel y Curie es la siguiente.
\[1 \mathrm{Ci}=3.7 \times 10^{10} \mathrm{~Bq}=3.7 \times 10^{10} \text { disintegrations }\nonumber\]
A menudo el radioisótopo para uso médico tiene la información de milicurie por mililitro (MCi/ml) a partir de la cual se puede calcular el volumen para la dosis deseada.
Al paciente se le debe administrar una dosis de 5.0 mCi de yodo-131 que está disponible como solución de Na 131 I que contiene 3.8 mCi/ml. ¿Qué volumen de la solución se debe administrar?
Solución
Utilice el recíproco de 3.8 mCi/ml como factor de conversión:
\[5.0 \cancel{\mathrm{~mCi}} \times \frac{1 \mathrm{~mL}}{3.8 \cancel{\mathrm{~mCi}}}=1.3 \mathrm{~mL} \text { dose }\nonumber\]
Mediciones de exposición a radiación
Dosis absorbida
La dosis de radiación ionizante o llamada dosis absorbida se mide en términos de energía depositada por radiación ionizante en una masa unitaria de materia que se está irradiando, como se ilustra en la Fig. 8.4.3
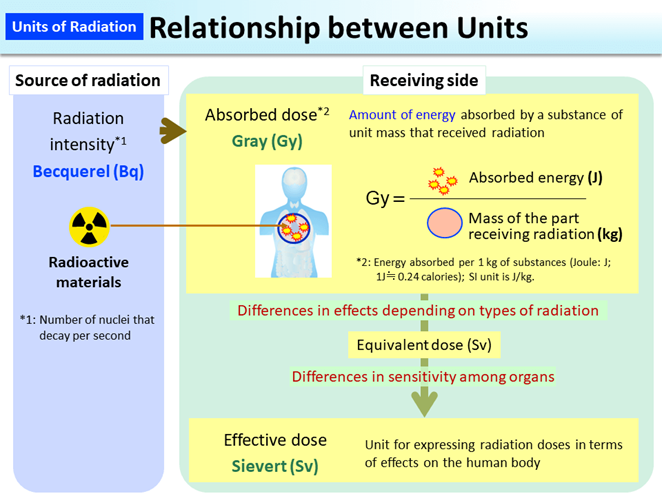
La unidad SI de dosis absorbida es gris (Gy) que se define como la absorción de un julio de energía de radiación por kilogramo de materia (J/kg).
La unidad común de dosis absorbida es rad, que significa dosis absorbida por radiación. El rad es una centésima parte de un gris, es decir:
\[1 \mathrm{~Gy}=100 \mathrm{~rad}\nonumber\]
Dosis equivalente
La misma cantidad de energía depositada en los tejidos por diferentes tipos de radiación conlleva diferentes niveles de riesgos para la salud en términos de causar cáncer y daño genético, expresado como factor de ponderación de radiación (W R), como se ilustra en la Fig. 8.4.4, y enumerado en la Fig. 8.4.5. Por ejemplo, 1 Gy\(\ce{beta}\) de partículas conlleva un riesgo de 5.5% de posibilidades de desarrollar eventualmente cáncer, mientras que 1 Gy de\(\ce{alpha}\) partículas tiene 20 veces más riesgo en comparación con la partícula β (ref.: https://en.Wikipedia.org/wiki/Sievert, consultada el 15/07/2020). El riesgo para la salud de la radiación ionizante se mide en las unidades de dosis equivalente. Sievert (Sv) es una unidad SI de una dosis equivalente de radiación ionizante que mide los efectos sobre la salud de los bajos niveles de radiación ionizante en el cuerpo humano.
La dosis equivalente en Sievert (Sv) es igual al producto de la dosis absorbida en grises (Gy) multiplicado el factor de ponderación de radiación (W R), es decir,\(\text { The equivalent dose in } \mathrm{Sv}=\text { Absorbed dose in } \mathrm{Gy} \times \mathrm{W}_{\mathrm{R}}\)


La unidad común de dosis equivalente es rem (rem significa roentgen equivalente hombre), que es:
\[1 \mathrm{~Sv}=100 \mathrm{rem}\nonumber\]
Se requiere que el personal que trabaje en un ambiente de radiación lleve placas de película o dosímetros personales electrónicos, como se muestra en la Fig. 8.4.6, que registren la dosis recibida. Por lo general, las instalaciones de radiación mantienen un registro de la dosis de cada persona para cumplir con los límites de exposición permitidos a la radiación.

Dosis efectiva
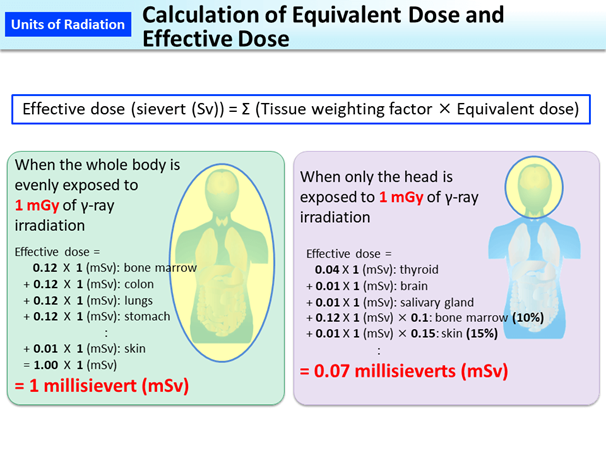
La dosis equivalente es igual a la dosis efectiva en sievert (Sv) cuando todo el cuerpo humano está expuesto por igual a la radiación. Si parte del cuerpo está expuesto, entonces se calcula una dosis efectiva en sievert (Sv) mediante la suma del producto de dosis equivalente en Sv con factor de ponderación tisular (W T) para cada tejido expuesto a la radiación, como se ilustra en la Fig. 8.4.4 y calculado con ejemplo en la Fig. 8.4.7. La razón de este cálculo es que el efecto de la misma dosis equivalente es diferente en diferentes tejidos. Los factores de ponderación tisular (W T) se enumeran en la Tabla 1.
Una dosis efectiva toma la dosis absorbida y la ajusta para el tipo de radiación y la sensibilidad de los órganos, es decir:
\[\text { The effective dose in } \mathrm{Sv}=\text { Equivalent dose in } \mathrm{Sv} \times \mathrm{W}_{\mathrm{T}}\nonumber\]
|
Órganos |
W T |
|---|---|
|
Gónadas |
0.08 |
|
Médula ósea roja |
0.12 |
|
Colón |
0.12 |
|
Pulmón |
0.12 |
|
Estómago |
0.12 |
|
Pechos |
0.12 |
|
Vejiga |
0.04 |
|
Hígado |
0.04 |
|
Esófago |
0.04 |
|
Tiroides |
0.04 |
|
Piel |
0.01 |
|
Superficie ósea |
0.01 |
|
Glándulas salivales |
0.01 |
|
Cerebro |
0.01 |
|
Resto del cuerpo |
0.12 |
|
Total |
1.00 |


