1.5: Error aleatorio

Objetivos de aprendizaje

Después de leer este capítulo, podrás hacer lo siguiente:

1. Definir error aleatorio y diferenciarlo del sesgo
2. Ilustrar errores aleatorios con ejemplos
3. Interpretar un valor p
4. Interpretar un intervalo de confianza
5. Diferenciar entre errores estadísticos tipo 1 y tipo 2 y explicar cómo se aplican a la investigación epidemiológica
6. Describir cómo el poder estadístico afecta la investigación

En este capítulo, cubriremos el error aleatorio —de dónde viene, cómo lo tratamos y qué significa para la epidemiología.

¿Qué es el error aleatorio?

En primer lugar, el error aleatorio no es sesgo. El sesgo es error sistemático y se trata con mayor detalle en el capítulo 6.

Error aleatorio es justo lo que parece: errores aleatorios en los datos. Todos los datos contienen errores aleatorios, porque ningún sistema de medición es perfecto. La magnitud de los errores aleatorios depende en parte de la escala en la que se mide algo (los errores en las mediciones a nivel molecular serían del orden de los nanómetros, mientras que los errores en las mediciones de altura humana son probablemente del orden de uno o dos centímetros) y en parte de la calidad de las herramientas utilizadas. Los laboratorios de física y química tienen escalas costosas y altamente precisas que pueden medir la masa al gramo, microgramo o nanogramo más cercano, mientras que la escala promedio en el baño de alguien probablemente sea precisa dentro de media libra o libra.

Para envolver tu cabeza alrededor de un error aleatorio, imagina que estás horneando un pastel que requiere 6 cucharadas de mantequilla. Para obtener las 6 cucharadas de mantequilla (tres cuartas partes de un palo, si hay 4 palos en una libra, como suele ser cierto en EU), podrías usar las marcas que aparecen en el papel encerado alrededor del palo, asumiendo que están alineadas correctamente. O quizás podrías seguir el método de mi madre, que es desenvolver el palo, hacer una ligera marca en lo que parece la mitad del palo, y luego llegar a las tres cuartas partes mirando la mitad de la mitad. O podrías usar mi método, que es hacer un globo ocular la marca de tres cuartos desde el principio y recortarla. Cualquiera de estos métodos de “medición” te dará aproximadamente 6 cucharadas de mantequilla, lo que sin duda es lo suficientemente bueno para el propósito de hornear un pastel, pero probablemente no valga exactamente 3 onzas, que es la cantidad de 6 cucharadas de mantequilla que pesan en Estados Unidos. ^[i] La medida en que esta vez estés un poco más de 3 onzas y quizás un poco por debajo de las 3 onzas la próxima vez está causando un error aleatorio en tu medición de mantequilla. Si siempre subestimaste o siempre sobrestimaste, entonces eso sería un sesgo, sin embargo, tus mediciones consistentemente subestimadas o sobreestimadas contendrían dentro de sí mismas un error aleatorio.

Variabilidad Inherente

Para cualquier variable dada que podamos querer medir en epidemiología (por ejemplo, altura, GPA, frecuencia cardíaca, número de años trabajando en una fábrica en particular, nivel de triglicéridos séricos, etc.), esperamos que haya variabilidad en la muestra, es decir, no esperamos que todos en la población tengan exactamente el mismo valor. Esto no es un error aleatorio. El error aleatorio (y sesgo) ocurre cuando tratamos de medir estas cosas. En efecto, la epidemiología como campo se basa en esta variabilidad inherente. Si todos fueran exactamente iguales, entonces no podríamos identificar qué tipo de personas tienen un mayor riesgo de desarrollar una enfermedad en particular.

En epidemiología, a veces nuestras mediciones dependen de que un ser humano distinto del participante del estudio mida algo sobre o sobre el participante. Los ejemplos incluirían la altura o el peso medidos, la presión arterial o el colesterol sérico. Para algunos de estos (por ejemplo, peso y colesterol sérico), el error aleatorio se arrastra en los datos debido al instrumento que se está utilizando, aquí, una escala que probablemente tenga una fluctuación de media libra, o un ensayo de laboratorio con un margen de error de unos pocos miligramos por decilitro. Para otras mediciones (por ejemplo, altura y presión arterial), el propio medidor es responsable de cualquier error aleatorio, como en el ejemplo de la mantequilla.

Sin embargo, muchas de nuestras mediciones se basan en el autoinforme de los participantes. Hay libros de texto completos y clases dedicadas al diseño de cuestionarios, y la ciencia detrás de cómo obtener los datos más precisos de las personas a través de los métodos de encuesta es bastante buena. El Pew Research Center ofrece un bonito tutorial introductorio sobre el diseño de cuestionarios en su sitio web.

Relevante para nuestra discusión aquí, el error aleatorio también aparecerá en los datos del cuestionario. Para algunas variables, habrá menos errores aleatorios que otras (por ejemplo, la raza autoinformada probablemente sea bastante precisa), pero todavía habrá algunos, por ejemplo, personas que marquen accidentalmente la casilla equivocada. Para otras variables, habrá más error aleatorio (por ejemplo, respuestas imprecisas a preguntas como, “En el último año, ¿cuántas veces al mes comiste arroz?”). Una buena pregunta para hacerse al considerar la cantidad de error aleatorio que podría estar en una variable derivada de un cuestionario es: “¿La gente me puede decir esto?” La mayoría de la gente teóricamente podría decirte cuánto durmieron anoche, pero sería difícil decirte cuánto duermen la misma noche de hace un año. Que te digan o no es un asunto diferente y toca sesgo (ver capítulo 6). Independientemente, el error aleatorio en los datos del cuestionario aumenta a medida que disminuye la probabilidad de que las personas puedan decirte la respuesta.

Cuantificación de errores aleatorios

Si bien podemos y deberíamos trabajar para minimizar los errores aleatorios (usando instrumentos de alta calidad, capacitando al personal sobre cómo tomar medidas, diseñar buenos cuestionarios, etc.), nunca se puede eliminar por completo. Por suerte, podemos usar estadísticas para cuantificar los errores aleatorios presentes en un estudio. En efecto, para eso están las estadísticas. En este libro, cubriré solo una pequeña porción del vasto campo de la estadística: interpretación de valores p e intervalos de confianza (IC). En lugar de centrarme en cómo calcularlos ^[1], me centraré en lo que significan (y lo que no significan). El conocimiento de los valores p e IC es suficiente para permitir una interpretación precisa de los resultados de los estudios epidemiológicos para estudiantes principiantes de epidemiología.

p -valores

Al realizar investigaciones científicas de cualquier tipo, incluida la epidemiología, se inicia con una hipótesis, que luego se prueba a medida que se realiza el estudio. Por ejemplo, si estamos estudiando estatura promedio de estudiantes de pregrado, nuestra hipótesis (generalmente indicada por H ₁) podría ser que los estudiantes varones son, en promedio, más altos que las estudiantes femeninas. Sin embargo, para fines de pruebas estadísticas, debemos reformular nuestra hipótesis como hipótesis nula ^[2]. En este caso, nuestra hipótesis nula (generalmente indicada por H ₀) sería la siguiente:

H ₀: No hay diferencia en la estatura media entre estudiantes de pregrado de sexo masculino y femenino.

Entonces emprenderíamos nuestro estudio para probar esta hipótesis. Primero se determina la población objetivo (estudiantes de pregrado) y se extrae una muestra de esta población. Luego medimos las alturas y géneros de todos en la muestra, y calculamos la estatura media entre los hombres versus la de las mujeres. Luego realizaríamos una prueba estadística para comparar las alturas medias en los 2 grupos. Debido a que tenemos una variable continua (estatura) medida en 2 grupos (hombres y mujeres), usaríamos una prueba t ^[3], y el estadístico t calculado a través de esta prueba tendría un valor p correspondiente, que es lo que realmente nos importa.

Un valor p es la probabilidad de que si repitieras el estudio, encontraras un resultado al menos como extremo, asumiendo que la hipótesis nula es verdadera.

Digamos que en nuestro estudio encontramos que los estudiantes varones tienen un promedio de 5 pies y 10 pulgadas, y entre las alumnas la estatura media es de 5 pies y 6 pulgadas (para una diferencia de 4 pulgadas), y calculamos un valor p de 0.04. Esto significa que si realmente no hay diferencia en la estatura promedio entre estudiantes varones y estudiantes femeninas (es decir, si la hipótesis nula es cierta) y repetimos el estudio (todo el camino de regreso a dibujar una nueva muestra de la población), hay un 4% de probabilidad de que volvamos a encontrar una diferencia en la estatura media de 4 pulgadas o más.

Existen varias implicaciones que derivan del párrafo anterior. Primero, en epidemiología siempre calculamos valores de p de 2 colas. Aquí esto simplemente significa que el 4% de probabilidad de una diferencia de altura de ≥4 pulgadas no dice nada sobre qué grupo es más alto, solo que un grupo (ya sea machos o hembras) será más alto en promedio en al menos 4 pulgadas. Segundo, los valores p no tienen sentido si resulta que puedes inscribir a toda la población en tu estudio. Como ejemplo, digamos que nuestra pregunta de investigación se refiere a estudiantes de Salud Pública 425 (H425, Fundamentos de Epidemiología) durante el trimestre de invierno 2020 en la Universidad Estatal de Oregón (OSU). ¿Los hombres o las mujeres son más altos en esta población? Como la población es bastante pequeña y todos los miembros son fácilmente identificados, podemos inscribir a todos en lugar de tener que depender de una muestra. Todavía habrá error aleatorio en la medición de la altura, pero ya no usamos un valor p para cuantificarlo. Esto es porque si tuviéramos que repetir el estudio, encontraríamos exactamente lo mismo, ya que en realidad medimos a todos en la población. Los valores P solo aplican si estamos trabajando con muestras.

Finalmente, tenga en cuenta que el valor p describe la probabilidad de sus datos, asumiendo que la hipótesis nula es cierta, no describe la probabilidad de que la hipótesis nula sea verdadera dados sus datos. Este es un error de interpretación común cometido tanto por lectores principiantes como senior de estudios epidemiológicos. El valor p no dice nada sobre lo probable que es que la hipótesis nula sea verdadera (y por lo tanto, por otro lado, sobre la verdad de tu hipótesis real). Más bien, cuantifica la probabilidad de obtener los datos que obtuviste si la hipótesis nula pasara a ser cierta. Esta es una distinción sutil pero muy importante.

Significancia estadística

¿Qué pasa después? Tenemos un valor p, que nos dice la posibilidad de obtener nuestros datos dada la hipótesis nula. Pero, ¿qué significa eso en términos de qué concluir sobre los resultados de un estudio? En salud pública e investigación clínica, la práctica estándar es utilizar p ≤ 0.05 para indicar significancia estadística. Es decir, décadas de investigadores en este campo han decidido colectivamente que si la posibilidad de cometer un error tipo I (más sobre eso a continuación) es del 5% o menos, “rechazaremos la hipótesis nula”. Continuando con el ejemplo de altura desde arriba, concluiríamos así que existe una diferencia de estatura entre géneros, al menos entre estudiantes de pregrado. Para valores p superiores a 0.05, “fallamos en rechazar la hipótesis nula”, y en su lugar concluimos que nuestros datos no aportaron evidencia de que existiera una diferencia de estatura entre estudiantes de pregrado masculinos y femeninos.

No Rechazar el Nulo vs Aceptar el Nulo

Si p > 0.05, fallamos en rechazar la hipótesis nula. Nunca aceptamos la hipótesis nula porque es muy difícil probar la ausencia de algo. “Aceptar” la hipótesis nula implica que hemos probado que realmente no hay diferencia de estatura entre estudiantes varones y mujeres, que no es lo que pasó. Si p > 0.05, simplemente significa que no encontramos evidencia en oposición a la hipótesis nula, no que dicha evidencia no exista. Podríamos haber obtenido una muestra rara, podríamos haber tenido una muestra demasiado pequeña, etc. Hay todo un campo de investigación clínica (investigación de efectividad comparativa ^vi) dedicado a demostrar que un tratamiento no es mejor o peor que otro; los métodos del campo son complejos y los tamaños de muestra requeridos son bastante grandes. Para la mayoría de los estudios epidemiológicos, simplemente nos apegamos a no rechazar.

¿El corte p ≤ 0.05 es arbitrario? Absolutamente. Esto vale la pena tenerlo en cuenta, particularmente para los valores p muy cercanos a este punto de corte. ¿Es 0.49 realmente tan diferente de 0.51? Probablemente no, pero están en lados opuestos de esa línea arbitraria. El tamaño de un valor p depende de 3 cosas: el tamaño de la muestra, el tamaño del efecto (es más fácil rechazar la hipótesis nula si la verdadera diferencia de altura, si mediéramos a todos en la población, en lugar de solo nuestra muestra, es de 6 pulgadas en lugar de 2 pulgadas), y la consistencia de los datos, la mayoría comúnmente medido por las desviaciones estándar alrededor de las alturas medias en los 2 grupos. Por lo tanto, un valor p de 0.51 casi con certeza podría hacerse más pequeño simplemente inscribiendo a más personas en el estudio (esto se refiere al poder, que es la inversa del error tipo II, que se discute a continuación). Es importante tener en cuenta este hecho cuando leas estudios.

Estadística Frecuencista versus Bayesiana

Las pruebas de significancia estadística son parte de una rama de la estadística conocida como estadística frecuentista. ⁱⁱ Aunque extremadamente común en epidemiología y campos afines, esta práctica no se considera generalmente como una ciencia ideal, por varias razones. En primer lugar, el corte 0.05 es totalmente arbitrario, ⁱⁱⁱ y las pruebas de significancia estrictas rechazarían el nulo para p = 0.049 pero no rechazarían para p = 0.051, aunque sean casi idénticos. Segundo, hay muchos más matices a la interpretación de los valores p e intervalos de confianza que los que he cubierto en este capítulo. ^iv Por ejemplo, el valor p realmente está probando todos los supuestos de análisis, no solo la hipótesis nula, y un gran valor p a menudo indica simplemente que los datos no pueden discriminar entre numerosas hipótesis competidoras. No obstante, dado que tanto la salud pública como la medicina clínica requieren decisiones de sí o no (¿Deberíamos gastar recursos en esa campaña de educación para la salud? ¿Debería este paciente recibir este medicamento?) , tiene que haber algún sistema para decidir si o no, y actualmente lo es la prueba de significancia estadística. Hay otras formas de cuantificar el error aleatorio, y de hecho las estadísticas bayesianas (que en lugar de una respuesta de sí o no arroja una probabilidad de que algo suceda) ⁱⁱ se está volviendo cada vez más popular. Sin embargo, como las estadísticas frecuencistas y las pruebas de hipótesis nulas siguen siendo, con mucho, los métodos más utilizados en la literatura epidemiológica, son el foco de este capítulo.

Errores Tipo I y Tipo II

Un error tipo I (generalmente simbolizado por α, la letra griega alfa, y estrechamente relacionado con los valores p) es la probabilidad de que rechaces incorrectamente la hipótesis nula —en otras palabras, que “encuentres” algo que realmente no está ahí. Al elegir 0.05 como nuestro corte de significancia estadística, en los campos de la salud pública y la investigación clínica hemos acordado tácitamente que estamos dispuestos a aceptar que el 5% de nuestros hallazgos serán realmente errores tipo I, o falsos positivos.

Un error de tipo II (generalmente simbolizado por β, la letra griega beta) es lo contrario: β es la probabilidad de que falle incorrectamente al rechazar la hipótesis nula, es decir, se olvida de algo que realmente está ahí.

Poder = 1 — β y se interpreta como la probabilidad de que encuentres cosas si están ahí.

El poder en los estudios epidemiológicos varía ampliamente: idealmente debería ser de al menos 90% (es decir, la tasa de error tipo II es de 10%), pero muchas veces es mucho menor. La potencia es proporcional al tamaño de la muestra pero de manera exponencial: la potencia aumenta a medida que aumenta el tamaño de la muestra, pero para obtener de 90 a 95% de potencia se requiere un salto mucho mayor en el tamaño de la muestra que pasar de 40 a 45% de potencia. Si un estudio no rechaza la hipótesis nula, pero los datos parecen que podría haber una gran diferencia entre grupos, a menudo el problema es que el estudio tenía poca potencia, y con una muestra más grande, el valor p probablemente caería por debajo del corte mágico 0.05. Por otro lado, parte del problema con las muestras pequeñas es que por casualidad podrías haber obtenido una muestra no representativa, y agregar participantes adicionales no conduciría los resultados hacia la significación estadística. Como ejemplo, supongamos que nuevamente nos interesan las diferencias de altura de género, pero esta vez sólo entre deportistas colegiados. Comenzamos con un estudio muy pequeño, solo un equipo masculino y un equipo femenino. Si por casualidad elegimos, digamos, el equipo de básquetbol masculino y el equipo de gimnasia femenino, es probable que encontremos una enorme diferencia en las alturas medias, quizás de 18 pulgadas o más. Agregar otros equipos a nuestro estudio sería casi seguro que resultaría en una diferencia mucho más estrecha en las alturas medias, y la diferencia de 18 pulgadas “encontrada” en nuestro pequeño estudio inicial no se aguantaría con el tiempo.

Intervalos de confianza

Debido a que hemos establecido el nivel aceptable en 5%, en epidemiología y campos relacionados, lo más común es usar intervalos de confianza del 95% (IC 95%). Se puede usar un IC 95% para hacer pruebas de significancia: si el IC 95% no incluye el valor nulo (0 para diferencia de riesgo y 1.0 para odds ratios, ratios de riesgo y ratios de tasa), entonces p < 0.05, y el resultado es estadísticamente significativo.

Aunque el IC 95% se puede utilizar para las pruebas de significancia, contienen mucha más información que solo si el valor p es <0.05 o no. La mayoría de los estudios epidemiológicos reportan IC 95% alrededor de cualquier punto estimado que se presente. La interpretación correcta de un IC 95% es la siguiente:

Si repitiste el estudio 100 veces (volviste a sacar tu muestra de la población), y el estudio está libre de todo sesgo, entonces 95 de esas 100 veces el IC que calculas incluirían la respuesta “real” que obtendrías si pudieras inscribir a todos en la población.

También podemos ilustrar esto visualmente:

Figura\(\PageIndex{1}\): https://es.Wikipedia.org/wiki/Intervalo_de_confianza

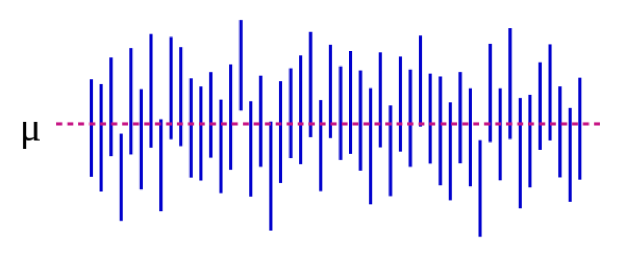
En la Figura 5-1, el parámetro poblacional μ representa la respuesta “real” que obtendrías si pudieras inscribir absolutamente a todos en la población en el estudio. Estimamos μ con datos de nuestra muestra. Continuando con nuestro ejemplo de altura, esto podría ser de 5 pulgadas: si pudiéramos medir mágicamente las alturas de cada estudiante de pregrado en Estados Unidos (o del mundo, dependiendo de cómo definas tu población objetivo), la diferencia media entre estudiantes masculinos y femeninos sería de 5 pulgadas. Es importante destacar que este parámetro de población casi siempre es inobservable; solo se vuelve observable si define su población de manera suficientemente estrecha como para poder inscribir a todos. Cada línea vertical azul representa el IC de un “estudio” individual —50 de ellos, en este caso. Los CI varían porque la muestra es ligeramente diferente cada vez; sin embargo, la mayoría de los CI (todos menos 3, de hecho) sí contienen μ.

Si realizamos nuestro estudio y encontramos una diferencia media de 4 pulgadas (IC 95%, 1.5 — 7), el CI nos dice 2 cosas. Primero, el valor p para nuestra prueba t sería <0.05, ya que el IC excluye 0 (el valor nulo en este caso, ya que estamos calculando una medida de diferencia). En segundo lugar, la interpretación del CI es: si repetimos nuestro estudio (incluyendo dibujar una nueva muestra) 100 veces, entonces 95 de esas veces nuestro CI incluiría el valor real (que sabemos aquí es de 5 pulgadas, pero que en la vida real no sabrías). Por lo tanto, mirar el CI aquí de 1.5 — 7.0 pulgadas da una idea de cuál podría ser la verdadera diferencia; casi con certeza se encuentra en algún lugar dentro de ese rango pero podría ser tan pequeño como 1.5 pulgadas o tan grande como 7 pulgadas. Al igual que los valores p, los CI dependen del tamaño de la muestra. Una muestra grande dará un IC comparativamente más estrecho. Los CI más estrechos se consideran mejores porque arrojan una estimación más precisa de cuál podría ser la respuesta “verdadera”.

Resumen

El error aleatorio está presente en todas las mediciones, aunque algunas variables son más propensas a ello que otras. Los valores P y los CI se utilizan para cuantificar el error aleatorio. Un valor p de 0.05 o menos generalmente se toma como “estadísticamente significativo”, y el IC correspondiente excluiría el valor nulo. Los CI son útiles para expresar el rango potencial del valor “real” a nivel de población que se estima.

---

Referencias

i. Mantequilla en EU y en el resto del mundo. Cocina Errens. Marzo 2014. https://www.errenskitchen.com/cookin...t-conversions/. Accedido septiembre 26, 2018. (Regreso)

ii. Enfoque bayesiano vs frecuentista: mismos datos, resultados opuestos. 365 Data Sci. Agosto 2017. https://365datascience.com/bayesian-...tist-approach/. Accedido octubre 17, 2018. (Regreso 1) (Regreso 2)

iii. Smith RJ. El uso continuado de las pruebas de significación de hipótesis nulas en antropología biológica. Am J Phys Anthropol. 2018; 166 (1) :236-245. doi:10.1002/ajpa.23399 (Regreso)

iv. Farland LV, Correia KF, Wise LA, Williams PL, Ginsburg ES, Missmer SA. Valores P y salud reproductiva: ¿qué pueden aprender los investigadores clínicos de la American Statistical Association? Hum Reprod Oxf Engl. 2016; 31 (11) :2406-2410. doi:10.1093/humrep/dew192 (Regreso)

v. Groenlandia S, Senn SJ, Rothman KJ, et al. Pruebas estadísticas, valores de p, intervalos de confianza y potencia: una guía para las malas interpretaciones. Eur J Epidemiol. 2016; 31:337-350. doi:10.1007/s10654-016-0149-3

vi. ¿Por qué es importante la investigación de efectividad comparada Instituto de investigación de resultados centrados en el paciente. https://www.pcori.org/files/why-comp...arch-important. Accedido 17 de octubre de 2018. (Regreso)

---

1. No hay una sola fórmula para calcular un valor p o un CI. Más bien, las fórmulas cambian dependiendo de qué prueba estadística se esté aplicando. Cualquier texto introductorio de bioestadística que discuta qué métodos estadísticos usar y cuándo también proporcionaría la información correspondiente sobre el valor p y el cálculo de IC.
2. No pases demasiado tiempo tratando de averiguar por qué necesitamos una hipótesis nula; simplemente lo hacemos. El fundamento está enterrado en siglos de filosofía académica de los argumentos de la ciencia.
3. Cómo elegir la prueba correcta está más allá del alcance de este libro; vea cualquier libro sobre bioestadística introductoria.