2.2: Criptografía moderna
( \newcommand{\kernel}{\mathrm{null}\,}\)
Lo que aprenderás
- Las implicaciones de la longitud de una clave en la seguridad
- Qué es el software de fuente abierta y por qué es importante para la seguridad
La criptografía moderna no es algo que se hace a mano. Las computadoras lo hacen por uno, y los detalles de los algoritmos que emplean se encuentran más allá del alcance de este libro. Sin embargo, hay ciertos principios que ayudan a comprender mejor y a evaluar las herramientas de seguridad digital modernas.
Seguridad que requiere ataques de fuerza bruta
Los protocolos criptográficos modernos están diseñados para obligar al adversario (quien no posee la clave criptográfica) a emplear (casi) tanto tiempo como el que tomaría probar cada una de las claves posibles para descifrar el código. Recordemos que intentar cada una de las claves posibles se conoce como ataque de fuerza bruta. Los parámetros de un protocolo dado se eligen de manera que dicha cantidad de tiempo sea impráctica. Por lo general, el parámetro más importante es la longitud de la clave. Al igual que en el cifrado Vigenère, las claves más largas hacen necesario explorar más claves posibles para adivinar la clave correcta. Conforme pasa el tiempo y el poder y rapidez de procesamiento de las computadoras se incrementan, las claves deben ser más largas para garantizar que los ataques de fuerza bruta no sean factibles. Por esta razón, muchos protocolos criptográficos mencionarán el tamaño de la clave en términos del número de bits que se requiere para representar la clave. Las computadoras representan la información, incluyendo claves criptográficas, en binario (usando 0 y 1). Así como los números 0 a 9 representan los dígitos de un número decimal, los números 0 y 1 representan los bits de un número binario. ¿Cuántos números decimales de tres dígitos hay? 10 10 10 = 103 = 1000; es decir, los números del 0 al 999. De igual forma, hay 2 2 2 2 = 24 = 16 números binarios de cuatro bits.
Por ejemplo, el protocolo criptográfico AES se conoce como AES-128 o AES-256 cuando usa el protocolo con claves de cifrado de 128 bits o de 256 bits, respectivamente. En el AES-128 hay 2128 = 340282366920938463463374607431768211456 claves posibles. En el AES-256 hay 2256 = 115792089237316195423570985008687907853269984665640564039457584007913129639936 claves posibles. Intentar cada una de las posibles claves, o incluso una pequeña fracción de ellas, en el AES-256 es inviable en términos computacionales, incluso considerando el poder de cómputo de Estados-nación como Estados Unidos.
La secrecía no garantiza la seguridad
Desde tan temprano como el siglo XIX, los matemáticos han tenido como criterio estándar que los esquemas criptográficos deben ser suficientemente seguros, aunque el método usado no sea secreto. Esto se basa en el siguiente principio: Si la seguridad requiere que el método permanezca secreto, entonces se corre el riesgo de que todos los mensajes que se hayan cifrado o vayan a cifrarse con ese método alguna vez sean revelados si dicho método llega a descubrirse. Por otro lado, si el método solo requiere que la clave sea secreta, entonces solo se arriesga que los mensajes cifrados con esa clave en particular sean divulgados si se vulnera la clave.
La transparencia es lo que da seguridad
De hecho, entre más transparencia haya en un método criptográfico, más confianza puedes tener en su seguridad. Para comprender esto, considera cómo se crea un programa de cifrado (o cualquier programa de cómputo). Todo comienza con un algoritmo para hacer el cifrado. Un programador convierte este algoritmo en un código fuente de cómputo. Una computadora compila dicho código fuente en el programa o aplicación que se ejecuta en tu computadora o teléfono.

Un buen programador debería poder traducir de un algoritmo (1) al código fuente (2) y de vuelta. Un profesional de la seguridad podría evaluar la seguridad de un protocolo criptográfico con base en el algoritmo, pero también debería evaluar el código fuente para estar seguro de su correcta implementación (de que no hay errores o bugs, intencionales o no). Sin embargo, como usuario, solo se tendría acceso al programa compilado (3). Desafortunadamente, solo con el código compilado es imposible que persona alguna reproduzca el código fuente.
Por tanto, a menos que el código fuente esté disponible, nadie puede estar seguro de que las declaraciones de seguridad de una app sean ciertas. Por otro lado, tan solo con el programa compilado, un pirata informático puede intentar penetrar la seguridad de la app. Muchos proyectos de software ponen su código fuente a disposición del público; a dicho software se le conoce como software de código abierto e incluye muchos proyectos reconocidos, de seguridad y de otra naturaleza, como Signal, Firefox y Linux. La alternativa es el software de código cerrado, común en proyectos que buscan monetizar su producto a través de la venta de software propietario, como Safari, Internet Explorer, Windows y Mac OS. Aunque es posible evaluar la seguridad del software de código cerrado (por ejemplo, a través de auditorías privadas), es mucho más difícil hacerlo de forma continua. Los proyectos de código abierto están abiertos al escrutinio público, lo cual da todas las oportunidades para que cualquier problema de seguridad (o de otra naturaleza) sea descubierto.
Proteger tu clave criptográfica da seguridad
Puesto que el método de cifrado suele ser público en los protocolos criptográficos modernos, la seguridad se logra protegiendo la clave criptográfica. En la práctica, esto depende de dónde se localice la clave. En el caso de Signal, una app segura de mensajería instantánea, la clave criptográfica es un archivo en tu teléfono; esta protege tu teléfono. En el caso de un administrador de contraseñas que sincroniza tus contraseñas en la nube, la clave que encripta el archivo que almacena todas tus contraseñas se deriva de o está protegida por la contraseña con la cual accedes a tu administrador de contraseñas.
Desconfiar de la infraestructura da seguridad
Aquí se ilustra por qué el cifrado de extremo a extremo es tan importante en la mensajería privada. Esto se cubre con mayor detalle técnico en el capítulo El intermediario.
En la siguiente figura, Assata (izquierda) intenta enviar un mensaje (Los desposeídos, por Ursula K. Le Guin) a Bobby (derecha) a través de internet:
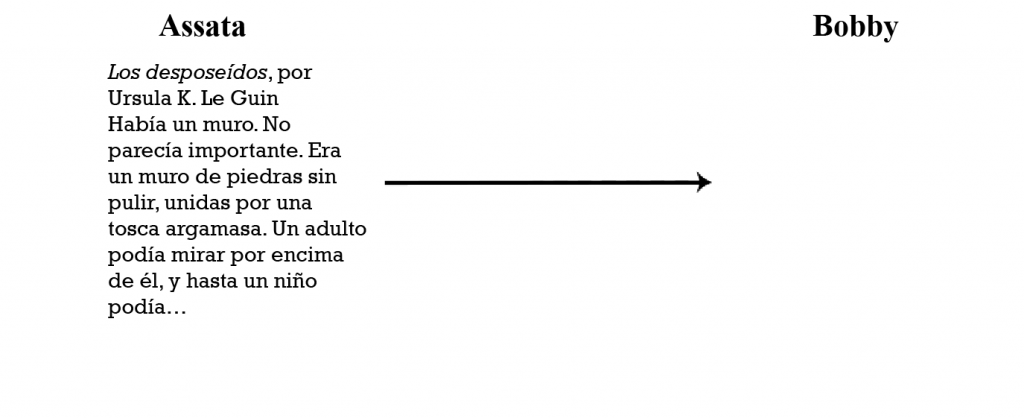
Pero el fantasma del malvado J. Edgar Hoover acecha la infraestructura. Este intermediario puede interceptar, leer y cambiar cualquier mensaje no protegido que se envíen nuestros dos amigos. Así:
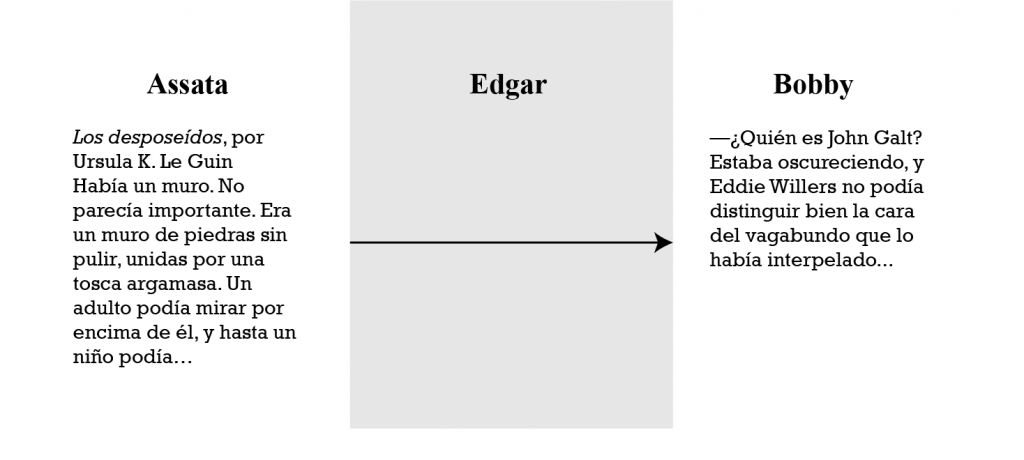
(Edgar también podría solo leer el mensaje y enviarlo sin alterarlo.) Para empeorar la situación, decir que una aplicación usa “cifrado” (sin especificar quién guarda las claves) no garantiza que los mensajes permanezcan privados y auténticos. Por ejemplo, si un servidor entre los dos camaradas administra las claves criptográficas, cualquiera con acceso al servidor podría leer y modificar todos los mensajes entre ellos. Sin embargo, si Assata y Bobby cifran sus mensajes (con la llave azul), entonces Edgar no podrá leerlos y no podrá reemplazar el mensaje con uno que pudiera descifrarse con la misma llave azul:
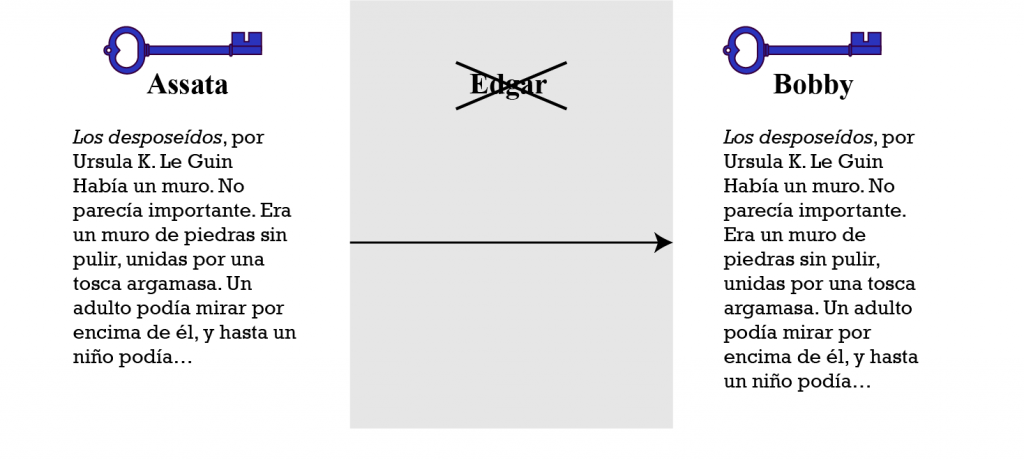
¿Cómo saber si una aplicación usa cifrado de extremo a extremo? El mejor indicador es que exista alguna forma de verificar las claves criptográficas. Signal facilita esto con números de seguridad. Esto se describe con más detalle en el capítulo Autenticarse mediante firmado criptográfico.
Otra forma de reducir la exposición a un intruso malicioso es usar la mensajería entre pares (P2P), donde se dice que “no hay un servidor” que administre tus mensajes o contactos. Sin embargo, incluso esto puede ser engañoso: existe una enorme cantidad de infraestructura de internet entre tú y tus amigos, invisible para la mayoría de los usuarios y apps. Como se acaba de describir, esta infraestructura es precisamente lo que el Estado explota para efectuar vigilancia en masa indetectable, sin despertar sospechas.
En contexto: La máquina Enigma
Es posible que las primeras técnicas modernas de cifrado se hayan usado durante la Segunda Guerra Mundial. Antes de las computadoras modernas, los protocolos eran respaldados por sofisticados aparatos mecánicos. El más notable de estos es la máquina Enigma, usada en la Alemania nazi. Enigma es un aparato electromecánico que permitía establecer una clave específica, teclear el texto en claro y generar el texto cifrado. Con la misma clave, se podía teclear el texto cifrado y generar el texto en claro original.

La clave involucra un cierto orden y posición inicial de los rotores (se muestran en la imagen). La operación normal requería usar una clave nueva todos los días, y las claves se enumeraban por día en manuales distribuidos entre los operadores de las máquinas Enigma; eran esencialmente libretas de un solo uso con claves. Por cierto, se imprimían en tinta soluble al agua, lo cual permitía la rápida destrucción del manual cuando había riesgo de que cayera en manos enemigas.
Se realizaron grandes esfuerzos para descifrar mensajes cifrados en la máquina Enigma. Varias máquinas Enigma fueron incautadas durante la Segunda Guerra Mundial, pero aun teniendo la máquina, descifrar los mensajes era casi imposible (como ocurre con cifrados modernos cuyos métodos son públicos). Alan Turing, uno de los fundadores de la ciencia de la computación como disciplina, trabajó en el reservado Bletchley Park, la sede central de decodificadores británicos durante la Segunda Guerra Mundial. Turing diseñó el Bombe, un tipo de computadora específicamente diseñada para descifrar mensajes Enigma. El Bombe no fue suficiente. De hecho, descifrar mensajes Enigma sin la clave es increíblemente difícil incluso con las capacidades modernas de cómputo; al menos un famoso mensaje Enigma interceptado durante la guerra permanece sin descifrar en la actualidad. Sin embargo, el Bombe, en combinación con el hecho de que la mayoría de los mensajes emitidos por la mañana contenían reportes del clima o la frase Keine besonderen Ereignisse (“nada que reportar”), permitió a los aliados descifrar mensajes Enigma en forma habitual.
Se ha estimado que el trabajo de Turing durante la guerra hizo posible acortarla más de dos años. Sin embargo, su trabajo permaneció sin reconocimiento durante su vida puesto que el trabajo hecho en Bletchley Park estaba reservado y, de hecho, se le criticó por no contribuir al esfuerzo de la guerra. Es aun más trágico que, como hombre homosexual, Turing fue perseguido por su propio gobierno hasta el punto de atribuirle un crimen en 1952. Acusado de cometer actos homosexuales, se le dio la opción de elegir la castración química o la prisión. Eligió lo primero, vivió otros dos años y supuestamente se suicidó por envenenamiento con cianuro.
Qué aprender a continuación
Recursos externos
- Caraco, Jean-Claude, Rémi Géraud-Stewart y David Naccache. “Kerckhoffs’ Legacy.” 2020.
Créditos
- source-code © OSU OERU is licensed under a CC BY-NC (Atribución NoComercial) license
- mitm-basic-1 © OSU OERU is licensed under a CC BY-NC (Atribución NoComercial) license
- mitm-basic-2 © OSU OERU is licensed under a CC BY-NC (Atribución NoComercial) license
- mitm-basic-3 © OSU OERU is licensed under a CC BY-NC (Atribución NoComercial) license
- Four-rotor-enigma © Greg Goebel is licensed under a Dominio público license


