2.7: Criptografía asimétrica
- Page ID
- 51874
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lo que aprenderás
- La diferencia entre la criptografía simétrica y la asimétrica
- Cómo funciona la criptografía asimétrica
Los protocolos criptográficos pueden clasificarse en dos categorías principales. En la criptografía simétrica, la clave que se usa para descifrar un mensaje es la misma que (o es fácil transformarla a partir de) la clave usada para cifrar el mensaje. Este es el caso de los cifrados básicos (César, Vigenère y la libreta de un solo uso) descritos en el capítulo ¿Qué es el cifrado? Aunque, por supuesto, hay cifrados simétricos modernos que se usan, por ejemplo, para cifrar los datos en tu teléfono o computadora. Como hemos visto, usar estos protocolos para comunicarse puede ser un reto puesto que primero debes encontrar una forma de intercambiar la clave con tu interlocutor de manera privada. El protocolo criptográfico Diffie-Hellman ofrece un método para que dos personas generen una clave compartida (la cual puede usarse en un protocolo criptográfico de clave simétrica) a través de un canal inseguro (como internet).
La criptografía de clave asimétrica o criptografía de clave pública resuelve el problema de compartir la clave en una forma diferente. En lugar de usar una sola clave para cifrar y descifrar, la criptografía asimétrica usa dos claves: una para cifrar (conocida como clave pública) y otra para descifrar (conocida como clave privada). Este par de claves tiene las siguientes propiedades:
- No es posible generar la clave privada a partir de la clave pública: ambas se generan juntas.
- Un mensaje cifrado con una clave pública solo podrá ser descifrado (factiblemente) con la clave privada correspondiente.
Supongamos que Bobby desea enviar a Assata un mensaje cifrado. Assata crea un par de claves privada/pública y le envía a Bobby su contraseña pública (por un canal inseguro). Bobby usa la clave pública para crear el texto cifrado y se lo envía a Assata. El texto cifrado solo podrá descifrarse usando la clave privada de Assata.
Aunque cualquiera puede tener la clave pública de Assata, lo único que puede hacerse con ella es cifrar mensajes que solo podrán descifrarse con la clave privada de Assata. Por tanto, la seguridad se garantiza manteniendo privada la clave privada: secreta y segura.
Con este modelo, cualquiera puede publicar su clave pública. Por ejemplo, Assata podría publicar su clave pública en línea de manera que cualquiera que desee enviarle un mensaje cifrado podría cifrarlo primero con su clave pública. De igual manera, Bobby podría crear su propio par de claves pública y privada y publicar su clave pública en línea para que otros puedan enviarle mensajes encriptados que sólo él podría descifrar con su clave privada (guardada de forma segura).
Repaso del protocolo Diffie-Hellman: ¿Criptografía asimétrica o simétrica?
Repasemos el protocolo Diffie-Hellman teniendo en mente las criptografías simétrica y asimétrica. Recordemos que Assata y Bobby acuerdan un número p de forma pública e insegura. Assata elige un número a (secreto) y calcula p ☆ a para enviárselo de manera pública e insegura a Bobby. Podríamos entonces considerar a como la clave privada de Assata, p ☆ a como su clave pública y este esquema como parte de un protocolo de clave asimétrica. Pero Bobby elige su propio número secreto b y lo combina con la clave pública de Assata para obtener p ☆ a ☆ b. De igual manera, Assata combina la “clave pública” de Bobby (p ☆ b) con su propia clave privada para obtener p☆ b ☆ a. Puesto que p ☆ a ☆ b = p ☆ b ☆ a, Assata y Bobby tienen una clave común que pueden usar para cifrar y descifrar. Así, esto forma parte de un protocolo de clave simétrica. Por dichas razones, el protocolo Diffie-Hellman se encuentra en algún lugar entre la criptografía de clave asimétrica y la criptografía de clave simétrica.
Combinar criptografía asimétrica y simétrica
La criptografía asimétrica suele ser más costosa en términos computacionales que la de clave simétrica. Para lograr las mismas garantías de seguridad (por ejemplo, contra ataques de fuerza bruta y otros ataques), las claves públicas asimétricas deben ser mucho más largas que las simétricas. Asimismo, el propio cifrado toma más tiempo usando claves asimétricas que claves simétricas. También existe el problema de que, mientras más tiempo usas una clave para cifrar, más ejemplos hay de texto cifrado que pueden usarse en intentos de romper el cifrado (que no sean de fuerza bruta); es decir, las claves tienden a caducar.
Por estas razones, las claves públicas suelen usarse para descifrar una clave simétrica para una determinada sesión (comunicación). Supongamos que Bobby desea enviarle a Assata un mensaje cifrado. Bobby genera una clave criptográfica simétrica y cifra el mensaje con ella usando un cifrado simétrico. Luego, cifra la clave simétrica con la clave pública de Assata y, finalmente, le envía el mensaje y la clave cifrados, como sigue:

Assata descifra la clave cifrada con su clave privada y usa el resultado para descifrar el texto cifrado, como sigue:
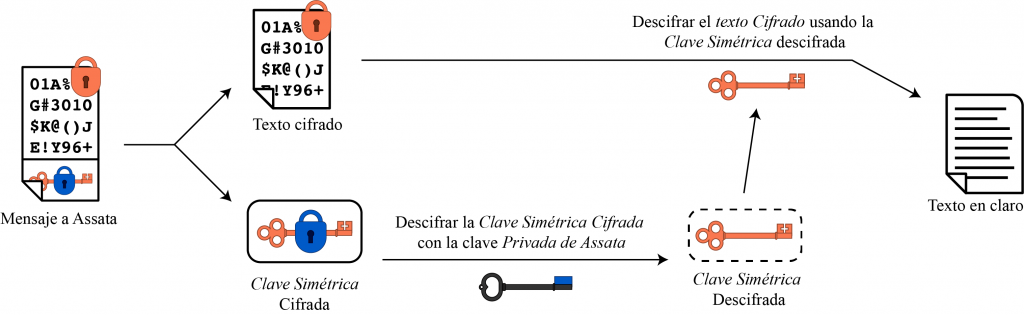
Puesto que la clave pública solo se usa para cifrar claves (que suelen ser secuencias de apariencia aleatoria), la clave pública no caduca ya que los métodos para romper el cifrado que dependen de frases en lenguaje humano fallarían. Un beneficio adicional es que, si se logra romper el cifrado de un mensaje, eso no ayuda a romper el cifrado de un mensaje diferente, puesto que cada mensaje se cifra con una clave distinta.
En contexto: Activismo antinuclear y Pretty Good Privacy
Una implementación bastante robusta de la criptografía asimétrica es PGP, siglas en inglés de la afirmación (que se queda corta) privacidad bastante buena. (Una versión interoperable, gratuita y de fuente abierta de PGP es GPG o GNU Privacy Guard.) El cifrado PGP suele usarse para cifrar comunicaciones por correo electrónico con varios plug-ins y clientes de correo que admiten cifrado PGP. Existen algunos directorios en línea (sincronizados) de claves PGP, cada una asociada con una dirección electrónica, que permiten a Bobby localizar la clave PGP de Assata para enviarle un correo cifrado.
Phil Zimmermann, un activista antinuclear por muchos años, creó PGP en 1991 para que personas con los mismos intereses pudieran usar servicios de tablón de anuncios (BBSs, el Reddit de los 80) y guardar mensajes de manera segura. Desarrolló PGP como un proyecto de fuente abierta, que no requería una licencia para su uso no comercial. Lo publicó inicialmente en un foro especializado en movimientos políticos comunitarios, principalmente en el movimiento por la paz. Así, PGP se abrió camino en un foro para distribuir código fuente y rápidamente encontró su salida de Estados Unidos. Usuarios y simpatizantes incluían disidentes en países totalitarios, promotores de libertades civiles y cypherpunks. Sin embargo, en ese tiempo, los criptosistemas que usaban claves de más de 40 bits eran considerados munición en la definición de la regulación de exportaciones de Estados Unidos. Inicialmente, PGP fue diseñado para admitir claves de 128 bits. En febrero de 1993, Zimmermann se volvió blanco de una investigación criminal formal del gobierno de EU por el cargo de “exportación de munición sin una licencia”. Zimmermann la enfrentó publicando todo el código fuente de PGP en un libro, el cual se distribuyó y vendió ampliamente. Cualquiera que deseara construir su propia copia de PGP podría simplemente quitar las tapas del libro, separar las páginas y escanearlas con un programa OCR, para crear un conjunto de archivos de texto de código fuente. En tanto que la exportación de munición (armas, bombas, aviones y software) estaba (y sigue estando) restringida, la exportación de libros está protegida por la Primera Enmienda. Después de varios años, la investigación sobre Zimmermann se cerró sin imputarle cargos criminales a él o a cualquier otro.
La legislación sobre exportaciones de criptografía desde Estados Unidos sigue siendo aplicable, pero se liberalizó sustancialmente a finales de los años 90 del siglo pasado. PGP ya no satisface la definición de un arma no exportable.
- Electronic Frontier Foundation. “A Deep Dive on End-to-End Encryption: How Do Public Key Encryption Systems Work?” Surveillance Self-Defense, 29 de septiembre de 2014.
- Zimmermann, Phil. “Why I Wrote PGP.” 1999.
Créditos
- public-key-cryptography-key-gen-share © OSU OERU is licensed under a CC BY-NC (Atribución NoComercial) license
- pubkeycrypto-split1-encrypt © OSU OERU is licensed under a CC BY-NC (Atribución NoComercial) license
- pubkeycrypto-split2-decrypt © OSU OERU is licensed under a CC BY-NC (Atribución NoComercial) license


