3.1: Conceptos matemáticos requeridos

Sistema Numeral y Notación

A menudo se dice que las matemáticas son el lenguaje de la ciencia. Si esto es cierto, entonces una parte esencial del lenguaje de las matemáticas son los números. El primer uso de los números ocurrió hace 100 siglos en el Medio Oriente para contar, o enumerar artículos. Los agricultores, ganaderos y comerciantes utilizaron fichas, piedras o marcadores para indicar una sola cantidad: una gavilla de grano, una cabeza de ganado o una longitud fija de tela, por ejemplo. Hacerlo hizo posible el comercio, lo que llevó a mejorar las comunicaciones y la difusión de la civilización.

Hace tres a cuatro mil años, los egipcios introdujeron fracciones. Primero los usaron para mostrar recíprocos. Posteriormente, los utilizaron para representar la cantidad cuando una cantidad se dividía en partes iguales.

Pero, ¿y si no hubiera ganado para comerciar o una cosecha entera de grano se perdiera en una inundación? ¿Cómo podría alguien indicar la existencia de nada? Desde los primeros tiempos, la gente había pensado en un “estado base” mientras contaba y utilizaba varios símbolos para representar esta condición nula. Sin embargo, no fue hasta aproximadamente el siglo V d.C. en la India que se agregó cero al sistema numérico y se utilizó como numeral en los cálculos.

Claramente, también era necesario que los números representaran pérdida o deuda. En la India, en el siglo VII d.C., se utilizaron números negativos como soluciones a ecuaciones matemáticas y deudas comerciales. Los opuestos de los números de conteo expandieron aún más el sistema numérico.

Debido a la evolución del sistema de números, ahora podemos realizar cálculos complejos utilizando estas y otras categorías de números reales. En esta sección, exploraremos conjuntos de números, cálculos con diferentes tipos de números y el uso de números en expresiones.

Números

Números naturales

Los números que usamos para contar, o enumerar ítems, son los números naturales: 1, 2, 3, 4, 5, y así sucesivamente. Los describimos en notación fija como {1,2,3,...} donde los puntos suspensivos (...) indican que los números continúan hasta el infinito. A los números naturales se les llama, por supuesto, también los números de conteo. Cada vez que enumeramos a los miembros de un equipo, contamos las monedas de una colección o contabilizamos los árboles en una arboleda, estamos usando el conjunto de números naturales.

Números enteros

Si sumamos cero a los números de conteo, obtenemos el conjunto de números enteros.

• Contando Números: 1, 2, 3,...
• Números Enteros: 0, 1, 2, 3,...

Enteros

Un conjunto de enteros suma los opuestos de los números naturales al conjunto de números enteros: {..., −3, −2, −1, 0, 1, 2, 3,...}. Es útil señalar que el conjunto de enteros se compone de tres subconjuntos distintos: enteros negativos, cero y enteros positivos. En este sentido, los enteros positivos son solo los números naturales. Otra forma de pensarlo es que los números naturales son un subconjunto de los enteros.

Fracciones

Muchas veces en la vida, las cantidades enteras no son exactamente lo que necesitamos. Un panadero debe usar un poco más que una taza de leche o parte de una cucharadita de azúcar. De manera similar, un carpintero podría necesitar menos de un pie de madera y un pintor podría usar parte de un galón de pintura. Estas personas necesitan usar números que forman parte de un todo. Estos números son muy útiles tanto en álgebra como en la vida cotidiana y se les llama facciones. De ahí que las Fracciones sean una forma de representar partes de un todo. Se escribe donde y son enteros y En una fracción, se llama el numerador y se llama denominador. El denominador representa el número de partes iguales en las que se ha dividido el conjunto, y el numerador representa cuántas partes se incluyen. El denominador, no puede ser igual a cero porque la división por cero es indefinida.

En (Figura), el círculo se ha dividido en tres partes de igual tamaño. Cada parte representa del círculo. Este tipo de modelo se llama círculo de fracción. Otras formas, como los rectángulos, también se pueden usar para modelar fracciones.

Hacer la actividad Matemáticas Manipulativas Fracciones Modelo te ayudará a desarrollar una mejor comprensión de las fracciones, sus numeradores y denominadores.

¿Qué representa la fracción? La fracción significa dos de tres partes iguales.

 

Un elemento interactivo o mediático ha sido excluido de esta versión del texto. Puedes verlo en línea aquí: http://pressbooks.oer.hawaii.edu/buildingmaint/?p=142

Fracciones impropias y adecuadas

En una fracción impropia, el numerador es mayor o igual que el denominador, por lo que su valor es mayor o igual a uno. Las fracciones como , ,, y se denominan fracciones impropias.

Cuando una fracción tiene un numerador que es menor que el denominador, se llama fracción propia, y su valor es menor que uno. Fracciones como , , y son fracciones propias.

Fracciones Equivalentes

Las fracciones equivalentes son fracciones que tienen el mismo valor. Por ejemplo, las fracciones y tienen el mismo valor, 1. En la figura se muestran dos imágenes: una sola pizza a la izquierda, cortada en dos trozos iguales, y una segunda pizza del mismo tamaño, cortada en ocho trozos a la derecha. Esta es una manera de demostrar que es equivalente a. En otras palabras, son fracciones equivalentes.

Figura #. Ya que la misma cantidad es de cada pizza está sombreada, vemos que es equivalente a.

Suma o resta fracciones

Para sumar o restar fracciones, deben tener un denominador común. Si las facciones tienen el mismo denominador, solo sumamos los numeradores y colocamos la suma sobre el denominador común. Si las fracciones tienen diferentes denominadores, ¿qué tenemos que hacer?

Primero, usaremos mosaicos de fracción para modelar encontrando el denominador común de y

Empezaremos con un azulejo y un azulejo. Queremos encontrar una baldosa de fracción común que podamos usar para que coincida con ambas y exactamente.

Si probamos las piezas, de ellas coinciden exactamente con la pieza, pero no coinciden exactamente con la pieza.

Si probamos las piezas, no cubren exactamente la pieza ni la pieza.

Si probamos las piezas, vemos que exactamente de ellas cubren la pieza, y exactamente de ellas cubren la pieza.

Si tuviéramos que probar las piezas, también funcionarían.

Azulejos aún más pequeños, como y también cubrirían exactamente la pieza y la pieza.

El denominador de la pieza más grande que cubre ambas fracciones es el mínimo denominador común (LCD) de las dos fracciones. Entonces, el mínimo común denominador de y es

Observe que todos los azulejos que cubren y tienen algo en común: Sus denominadores son múltiplos comunes de y los denominadores de y El múltiplo menos común (LCM) de los denominadores es y así decimos que es el mínimo común denominador (LCD) de las fracciones y. Por lo tanto, el mínimo común denominador (LCD) de dos fracciones es el mínimo común múltiplo (LCM) de sus denominadores.

Para encontrar el LCD de dos fracciones, encontraremos el LCM de sus denominadores. Seguimos el procedimiento que utilizamos anteriormente para encontrar el LCM de dos números. Solo usamos los denominadores de las fracciones, no los numeradores, al encontrar la LCD.

Ejemplo\(\PageIndex{1}\)

Encuentre la pantalla LCD para las fracciones y

Solución

Factorizar cada denominador en sus primos.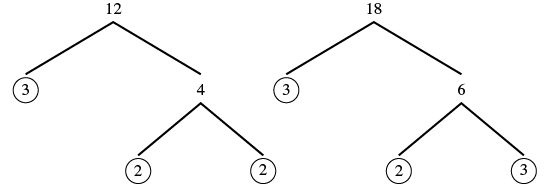
Enumere los primos de 12 y los primos de 18 alineándolos en columnas cuando sea posible.
Derriba las columnas.
Multiplicar los factores. El producto es el LCM.
El LCM de 12 y 18 es 36, por lo que el LCD de y es 36.	LCD de y es 36.

 

Truco de suma y resta de fracciones: ¡hazlas de la manera más rápida!

Consulta\(\PageIndex{1}\)

Multiplicar fracciones

Cuando multiplicamos fracciones, simplemente multiplicamos los numeradores y multiplicamos los denominadores directamente cruzados.

Un modelo puede ayudarte a entender la multiplicación de fracciones. Usaremos mosaicos de fracción para modelar Para multiplicar y pensar

Comience con baldosas de fracción por tres cuartas partes. Para encontrar la mitad de las tres cuartas partes, necesitamos dividirlas en dos grupos iguales. Como no podemos dividir las tres baldosas de manera uniforme en dos partes, las cambiamos por baldosas más pequeñas.

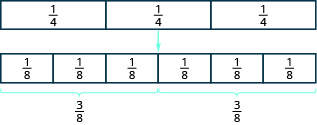
Vemos es equivalente a Tomar la mitad de las seis fichas nos da tres fichas, que es

Por lo tanto,

Al multiplicar fracciones, siguen aplicándose las propiedades de los números positivos y negativos. Es una buena idea determinar el signo del producto como primer paso. En Ejemplo\(\PageIndex{2}\) vamos a multiplicar dos negativos, por lo que el producto será positivo.

Ejemplo\(\PageIndex{2}\)

Multiplicar y escribir la respuesta en forma simplificada:

Solución

Agrega texto de ejemplo aquí.

Los signos son los mismos, por lo que el producto es positivo. Multiplicar los numeradores, multiplicar los denominadores.
Simplificar.
Busque factores comunes en el numerador y denominador. Reescritura mostrando factores comunes.
Eliminar factores comunes.	=

Otra forma de encontrar este producto consiste en eliminar factores comunes antes.

Determinar el signo del producto. Multiplicar.
Mostrar factores comunes y luego eliminarlos.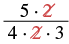
Multiplicar los factores restantes.

Obtenemos el mismo resultado.

Multiplicando dos fracciones: Ejemplo

 

Consulta\(\PageIndex{2}\)

Dividir fracciones

Ahora que sabemos multiplicar fracciones, estamos casi listos para dividirnos. Antes de que podamos hacer eso, que necesitamos algo de vocabulario.

El recíproco de una fracción se encuentra invirtiendo la fracción, colocando el numerador en el denominador y el denominador en el numerador. El recíproco de es.

Observe que · = 1. Un número y su recíproco se multiplican a 1.

Para obtener un producto de 1 positivo al multiplicar dos números, los números deben tener el mismo signo. Por lo que los recíprocos deben tener el mismo signo.

El recíproco de − es —, ya que −) = 1.

Dividiendo fracciones: Ejemplo

Consulta\(\PageIndex{3}\)

Decimales

Probablemente ya conozcas bastante de decimales en función de tu experiencia con el dinero. Supongamos que compra un sándwich y una botella de agua para el almuerzo. Si el sándwich cuesta, la botella de agua cuesta, y el impuesto total a las ventas es, ¿cuál es el costo total de tu almuerzo?

El total es Supongamos que pagas con factura y centavos. ¿Deberías esperar el cambio? No, y peniques es lo mismo que

Porque cada centavo vale de un dólar. Escribimos el valor de un centavo como desde

Los decimales son de hecho otra forma de escribir fracciones cuyos denominadores son poderes de 10.

Así como los números de conteo se basan en potencias de diez, los decimales se basan en potencias de diez. En el Cuadro 1 se muestran los números de conteo.

Tabla 1

Número de conteo	Nombre
	Uno
	Diez
	Cien
	Mil
	Diez mil

¿Cómo se relacionan los decimales con las fracciones? En el Cuadro 2 se muestra la relación.

Cuadro 2

Decimal	Fracción	Nombre
		Una décima
		Centésimas
		Una milésima
		Una diezmilésima

Sumar y restar decimales

Echemos un vistazo más a la orden del almuerzo desde el inicio de Decimales, esta vez notando cómo se sumaron los números.

Los tres artículos (sándwich, agua, impuestos) tenían un precio en dólares y centavos, así que alineamos los dólares por debajo de los dólares y los centavos por debajo de los centavos, con los decimales alineados entre ellos. Entonces acabamos de sumar cada columna, como si estuviéramos sumando números enteros. Al alinear decimales de esta manera, podemos sumar o restar los valores posicionales correspondientes tal como hicimos con números enteros.

Sumar o restar decimales.

1. Escribe los números verticalmente para que los puntos decimales se alineen.
2. Use ceros como portaposiciones, según sea necesario.
3. Sumar o restar los números como si fueran números enteros. Luego coloque el decimal en la respuesta debajo de los puntos decimales en los números dados.

Multiplicar decimales

Multiplicar decimales es muy parecido a multiplicar números enteros, solo tenemos que determinar dónde colocar el punto decimal. El procedimiento para multiplicar decimales tendrá sentido si primero revisamos multiplicar fracciones.

¿Recuerdas cómo multiplicar fracciones? Para multiplicar fracciones, multiplicas los numeradores y luego multiplicar los denominadores.

Entonces veamos qué obtendríamos como producto de los decimales al convertirlos primero en fracciones. Haremos dos ejemplos uno al lado del otro en la Tabla 3. Busca un patrón.

Cuadro 3

	A	B
Convertir a fracciones.
Multiplicar.
Vuelva a convertir a decimales.

Hay un patrón que podemos usar. En A, multiplicamos dos números que cada uno tenía un decimal, y el producto tenía dos decimales. En B, multiplicamos un número con un decimal por un número con dos decimales, y el producto tenía tres decimales.

¿Cuántos decimales esperarías para el producto de Si dijeras “cinco”, reconociste el patrón. Cuando multiplicamos dos números por decimales, contamos todos los decimales en los factores, en este caso dos más tres, para obtener el número de decimales en el producto, en este caso cinco.

Una vez que sabemos determinar el número de dígitos después del punto decimal, podemos multiplicar los números decimales sin convertirlos primero en fracciones. El número de decimales en el producto es la suma del número de decimales en los factores.

Las reglas para multiplicar números positivos y negativos también se aplican a los decimales, por supuesto.

Al multiplicar dos números,

• si sus signos son los mismos, el producto es positivo.
• si sus signos son diferentes, el producto es negativo.

Cuando multiplica decimales firmados, primero determina el signo del producto y luego multiplica como si los números fueran ambos positivos. Por último, escriba el producto con el letrero correspondiente.

Multiplicar números decimales

1. Determinar el signo del producto.
2. Escribe los números en formato vertical, alineando los números a la derecha.
3. Multiplique los números como si fueran números enteros, ignorando temporalmente los decimales.
4. Coloque el punto decimal. El número de decimales en el producto es la suma del número de decimales en los factores. Si es necesario, use ceros como marcadores de posición.
5. Escriba el producto con el letrero correspondiente.

Multiplicar decimales: Ejemplo

Consulta\(\PageIndex{4}\)

Multiplicar por Poderes de 10

En muchos campos, especialmente en las ciencias, es común multiplicar decimales por poderes de Veamos qué sucede cuando multiplicamos por algunos poderes de

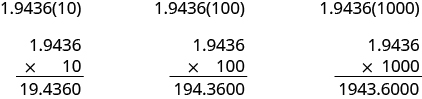
Mira los resultados sin los ceros finales. ¿Te das cuenta de un patrón?

El número de lugares que movió el punto decimal es el mismo que el número de ceros en la potencia de diez. En el Cuadro 4 se resumen los resultados.

Cuadro 4

Multiplicar por	Número de ceros	Número de lugares movimientos de punto decimal
		lugar a la derecha
		lugares a la derecha
		lugares a la derecha
		lugares a la derecha

Podemos usar este patrón como atajo para multiplicar por potencias de diez en lugar de multiplicar usando el formato vertical. Podemos contar los ceros en la potencia de y luego mover el punto decimal ese mismo de lugares a la derecha.

Entonces, por ejemplo, para multiplicar por mover los lugares decimales hacia la derecha.

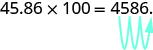
A veces cuando necesitamos mover el punto decimal, no hay suficientes cifras decimales. En ese caso, usamos ceros como marcadores de posición. Por ejemplo, vamos a multiplicar por Necesitamos mover los lugares decimales hacia la derecha. Dado que solo hay un dígito a la derecha del punto decimal, debemos escribir a en el lugar de centésimas.

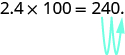
Multiplica un decimal por una potencia de 10.

1. Mover el punto decimal a la derecha el mismo número de lugares que el número de ceros en la potencia de
2. Escriba ceros al final del número como marcadores de posición si es necesario.

Dividir decimales

Al igual que con la multiplicación, la división de decimales es muy parecida a dividir números enteros. Sólo tenemos que averiguar dónde se debe colocar el punto decimal.

Para entender la división decimal, consideremos el problema de la multiplicación

Recuerde, un problema de multiplicación puede reformularse como un problema de división. Así podemos escribir

Podemos pensar en esto como “Si dividimos 8 décimas en cuatro grupos, ¿cuántos hay en cada grupo?”. La siguiente figura muestra que hay cuatro grupos de dos décimas en ocho décimas. Entonces

Usando notación de división larga, escribiríamos

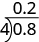
Observe que el punto decimal en el cociente está directamente por encima del punto decimal en el dividendo.

Para dividir un decimal por un número entero, colocamos el punto decimal en el cociente por encima del punto decimal en el dividendo y luego dividimos como de costumbre. A veces necesitamos usar ceros adicionales al final del dividendo para seguir dividiendo hasta que no haya resto.

Divide un decimal por un número entero.

1. Escribe como división larga, colocando el punto decimal en el cociente por encima del punto decimal en el dividendo.
2. Dividir como de costumbre.

Dividir un decimal por otro decimal

Hasta el momento, hemos dividido un decimal por un número entero. ¿Qué sucede cuando dividimos un decimal por otro decimal? Veamos el mismo problema de multiplicación que vimos antes, pero de una manera diferente.

Recuerde, nuevamente, que un problema de multiplicación puede reformularse como un problema de división. Esta vez nos preguntamos: “¿Cuántas veces entra en Porque podemos decir que va a cuatro veces? Esto quiere decir que dividido por

Obtendríamos la misma respuesta, si dividiéramos por ambos números enteros. ¿Por qué es así? Pensemos en el problema de la división como una fracción.

Multiplicamos el numerador y el denominador por y terminamos simplemente dividiendo por Para dividir decimales, multiplicamos tanto el numerador como el denominador por la misma potencia de para hacer del denominador un número entero. Debido a la Propiedad de Fracciones Equivalentes, no hemos cambiado el valor de la fracción. El efecto es mover los puntos decimales en el numerador y denominador el mismo número de lugares a la derecha.

También usamos las reglas para dividir números positivos y negativos con decimales. Al dividir decimales firmados, primero determinar el signo del cociente y luego dividir como si los números fueran ambos positivos. Por último, escribir el cociente con el signo correspondiente.

Puede ser útil revisar el vocabulario para la división:

Dividir los números decimales.

1. Determinar el signo del cociente.
2. Haga que el divisor sea un número entero moviendo el punto decimal hasta la derecha. Mueve el punto decimal en el dividendo el mismo número de lugares a la derecha, escribiendo ceros según sea necesario.
3. Dividir. Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo.
4. Escriba el cociente con el signo correspondiente.

Dividiendo decimales — Ejemplo

Consulta\(\PageIndex{5}\)

Exponentes

Un exponente indica multiplicación repetida de la misma cantidad. Por ejemplo, 24 significa multiplicar cuatro factores de 2, entonces 24 significa 2·2·2. Este formato se conoce como notación exponencial.

Notación exponencial

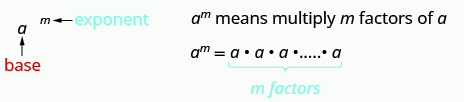
Esto se lee a la mésima potencia.

En la expresión am, el exponente nos dice cuántas veces usamos la base a como factor.

Cuadrado

¿Sabes por qué usamos la palabra cuadrado? Si construimos un cuadrado con tres mosaicos en cada lado, el número total de mosaicos sería nueve.

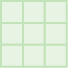
Es por ello que decimos que la plaza de tres es de nueve.

3 ² = 9

¿Qué pasa cuando cuadras un número negativo?

(-8) ² = (-8) (-8) = 64

Cuando multiplicamos dos números negativos, el producto siempre es positivo. Por lo que el cuadrado de un número negativo siempre es positivo.

Cube

Raíces Cuadradas

A veces tendremos que mirar a la inversa la relación entre los números y sus cuadrados. Porque 10 ² =100, decimos 100 es el cuadrado de 10. También podemos decir que 10 es una raíz cuadrada de 100.

Raíz cuadrada de un número

Un número cuyo cuadrado es m se llama raíz cuadrada de m.

Si n ² =m, entonces n es una raíz cuadrada de m.

Observe (−10) ² =100 también, por lo que −10 también es una raíz cuadrada de 100. Por lo tanto, tanto 10 como −10 son raíces cuadradas de 100.

Entonces, cada número positivo tiene dos raíces cuadradas: una positiva y otra negativa.

¿Y si solo queremos la raíz cuadrada positiva de un número positivo? El signo radical, √, representa la raíz cuadrada positiva. La raíz cuadrada positiva también se llama raíz cuadrada principal.

Notación de raíz cuadrada

√m se lee como “la raíz cuadrada de m.

Si m=n ², entonces m = n para n≥0. Si m = n ², entonces m= n para n≥0.

También podemos usar el signo radical para la raíz cuadrada de cero. Porque 0 ² =0, √0=0. Observe que cero tiene solo una raíz cuadrada.

Raíz cuadrada de un número negativo

¿Podemos simplificar √−25? ¿Hay un número cuyo cuadrado es −25?

() ² = −25?

Ninguno de los números que hemos tratado hasta ahora tiene un cuadrado que sea −25. ¿Por qué? Cualquier número positivo al cuadrado es positivo, y cualquier número negativo al cuadrado también es positivo. No hay un número real igual a −25. Si se nos pide encontrar la raíz cuadrada de cualquier número negativo, decimos que la solución no es un número real.

Estimar raíces cuadradas (hecho)

Hasta el momento sólo hemos trabajado con raíces cuadradas de cuadrados perfectos. Las raíces cuadradas de otros números no son números enteros.

Podríamos concluir que las raíces cuadradas de los números entre 4 y 9 estarán entre 2 y 3, y no serán números enteros. Con base en el patrón de la tabla anterior, podríamos decir que √5 está entre 2 y 3. Usando símbolos de desigualdad, escribimos 2<√5<3

Raíces Cuadradas Aproximadas con una Calculadora

Existen métodos matemáticos para aproximar raíces cuadradas, pero es mucho más conveniente usar una calculadora para encontrar raíces cuadradas. Encuentra la clave √ o √x en tu calculadora. Utilizarás esta clave para aproximar raíces cuadradas. Cuando usas tu calculadora para encontrar la raíz cuadrada de un número que no es un cuadrado perfecto, la respuesta que ves no es el número exacto. Se trata de una aproximación, al número de dígitos que se muestran en la pantalla de tu calculadora. El símbolo para una aproximación es ≈ y se lee aproximadamente.

Supongamos que su calculadora tiene una pantalla de 10 dígitos. Usarlo para encontrar la raíz cuadrada de 5 dará 2.236067977. Esta es la raíz cuadrada aproximada de 5. Cuando informamos la respuesta, debemos usar el signo “aproximadamente igual a” en lugar de un signo igual.

√5 ≈ 2.2360679785

Rara vez usará tantos dígitos para aplicaciones en álgebra. Entonces, si quisieras redondear √5 a dos decimales, escribirías

√5≈2.24

¿Cómo sabemos que estos valores son aproximaciones y no los valores exactos? Mira lo que sucede cuando los cuadramos.

2.236067978 ² = 5.000000002

2.24 ² = 5.0176

Los cuadrados están cerca, pero no exactamente iguales, a 5.

Introducción a los Exponentes

Consulta\(\PageIndex{6}\)

Ratios

Cuando solicites una hipoteca, el oficial de préstamos comparará tu deuda total con tus ingresos totales para decidir si calificas para el préstamo. Esta comparación se llama la relación deuda-ingresos. Una relación compara dos cantidades que se miden con la misma unidad. Si comparamos y, la relación se escribe como

Ratios que involucran decimales

A menudo trabajaremos con ratios de decimales, especialmente cuando tenemos ratios que involucran dinero. En estos casos, podemos eliminar los decimales usando la Propiedad de Fracciones Equivalentes para convertir la relación a una fracción con números enteros en el numerador y denominador.

Por ejemplo, considera la relación Podemos escribirla como una fracción con decimales y luego multiplicar el numerador y denominador por para eliminar los decimales.

¿Ves un atajo para encontrar la fracción equivalente? Observe eso y El mínimo común denominador de y es Al multiplicar el numerador y denominador de por 'movimos' los decimales dos lugares a la derecha para obtener la fracción equivalente sin decimales. Ahora que entendemos las matemáticas detrás del proceso, podemos encontrar la fracción sin decimales como esta:

“Mover” los decimales 2 lugares.
Simplificar.

No tienes que escribir cada paso cuando multiplicas el numerador y el denominador por potencias de diez. Siempre y cuando muevas ambos decimales el mismo número de lugares, la relación seguirá siendo la misma.

Consulta\(\PageIndex{7}\)

Perímetro, área y volumen

Perímetro y Área

El perímetro es una medida de la distancia alrededor de una figura. El área es una medida de la superficie cubierta por una figura.

Consulta\(\PageIndex{8}\)

Cuadrado

La siguiente figura muestra una baldosa cuadrada que mide 1 pulgada en cada lado. Si una hormiga caminara alrededor del borde de la baldosa, caminaría 4 pulgadas. Esta distancia es el perímetro de la baldosa. Dado que la loseta es un cuadrado que mide 1 pulgada en cada lado, su área es de una pulgada cuadrada. El área de una forma se mide determinando cuántas unidades cuadradas cubren la forma.

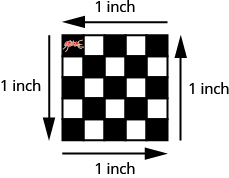
Figura #. Perímetro = 4 pulgadas Área = 1 pulgada cuadrada

Cuando la hormiga camina completamente alrededor de la loseta en su borde, está trazando el perímetro de la loseta. El área de la loseta es de 1 pulgada cuadrada.

Rectángulo

Un rectángulo tiene cuatro lados y cuatro ángulos rectos. Los lados opuestos de un rectángulo tienen la misma longitud. Nos referimos a un lado del rectángulo como la longitud, L, y el lado adyacente como el ancho, W. Ver figura a continuación.

Un rectángulo tiene cuatro lados y cuatro ángulos rectos. Los lados están etiquetados como L para longitud y W para ancho.

El perímetro, P, del rectángulo es la distancia alrededor del rectángulo. Si empezaste en una esquina y caminabas alrededor del rectángulo, caminarías unidades L+W+L+W, o dos longitudes y dos anchos. El perímetro entonces es

P=L+W+L+W

o

P=2+2W

¿Qué pasa con el área de un rectángulo? Recuerda la alfombra rectangular desde el inicio de esta sección. Tenía 2 pies de largo por 3 pies de ancho, y su área era de 6 pies cuadrados. Vea la Figura a continuación. Desde A=23, vemos que el área, A, es la longitud, L, por el ancho, W, por lo que el área de un rectángulo es A=LW.

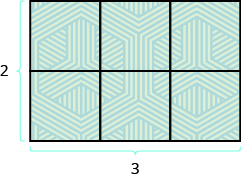
El área de esta alfombra rectangular es de 6 pies cuadrados, su longitud por su ancho.

Triángulo

Ahora sabemos cómo encontrar el área de un rectángulo. Podemos usar este hecho para ayudarnos a visualizar la fórmula para el área de un triángulo. En el rectángulo de la siguiente figura, hemos etiquetado la longitud b y la anchura h, por lo que su área es bh.

El área de un rectángulo es la base, b, veces la altura, h.

Podemos dividir este rectángulo en dos triángulos congruentes (ver figura abajo). Los triángulos que son congruentes tienen longitudes y ángulos laterales idénticos, por lo que sus áreas son iguales. El área de cada triángulo es la mitad del área del rectángulo, o bh. Este ejemplo nos ayuda a ver por qué la fórmula para el área de un triángulo es A= bh.

Un rectángulo se puede dividir en dos triángulos de igual área. El área de cada triángulo es la mitad del área del rectángulo.

La fórmula para el área de un triángulo es A = bh, donde b es la base y h es la altura.

Para encontrar el área del triángulo, es necesario conocer su base y altura. La base es la longitud de un lado del triángulo, generalmente el lado en la parte inferior. La altura es la longitud de la línea que conecta la base con el vértice opuesto, y forma un ángulo de 90° con la base. En la siguiente figura se muestran tres triángulos con la base y la altura de cada uno marcado.

La altura h de un triángulo es la longitud de un segmento de línea que conecta la base con el vértice opuesto y forma un ángulo de 90° con la base.

Triángulos isósceles y equiláteros

Además del triángulo rectángulo, algunos otros triángulos tienen nombres especiales. Un triángulo con dos lados de igual longitud se llama triángulo isósceles. Un triángulo que tiene tres lados de igual longitud se llama triángulo equilátero. La siguiente figura muestra ambos tipos de triángulos.

En un triángulo isósceles, dos lados tienen la misma longitud, y el tercer lado es la base. En un triángulo equilátero, los tres lados tienen la misma longitud.

Triángulos isósceles y equiláteros

• Un triángulo isósceles tiene dos lados de la misma longitud.
• Un triángulo equilátero tiene tres lados de igual longitud.

Trapecio

Un trapecio es una figura de cuatro lados, un cuadrilátero, con dos lados que son paralelos y dos lados que no lo son. Los lados paralelos se llaman bases. Llamamos a la longitud de la base menor b, y la longitud de la base más grande B. La altura, h, de un trapecio es la distancia entre las dos bases como se muestra en la siguiente figura.

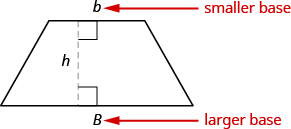
Un trapecio tiene una base más grande, B, y una base más pequeña, b. La altura h es la distancia entre las bases.

La fórmula para el área de un trapecio es:

_Trapezoide de área = 1/2h (B+b)

Dividir el trapecio en dos triángulos puede ayudarnos a entender la fórmula. El área del trapecio es la suma de las áreas de los dos triángulos. Consulte la figura a continuación.

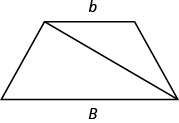
Dividir un trapecio en dos triángulos puede ayudarte a entender la fórmula para su área.

La altura del trapecio es también la altura de cada uno de los dos triángulos. Consulte la figura a continuación.

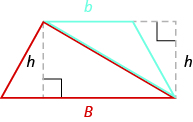
La fórmula para el área de un trapecio es

Si distribuimos, obtenemos,

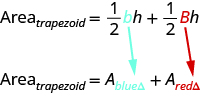
Círculo

Las propiedades de los círculos han sido estudiadas desde hace más de años. Todos los círculos tienen exactamente la misma forma, pero sus tamaños se ven afectados por la longitud del radio, un segmento de línea desde el centro hasta cualquier punto del círculo. Un segmento de línea que pasa por el centro de un círculo conectando dos puntos en el círculo se llama diámetro. El diámetro es dos veces más largo que el radio. Consulte la figura a continuación.

El tamaño de un círculo se puede medir de dos maneras. La distancia alrededor de un círculo se llama su circunferencia.

Arquímedes descubrió que para círculos de todos los tamaños diferentes, dividir la circunferencia por el diámetro siempre da el mismo número. El valor de este número es pi, simbolizado por letra griega (pastel pronunciado). Sin embargo, el valor exacto de no se puede calcular ya que el decimal nunca termina ni se repite (aprenderemos más sobre números como este en Las propiedades de los números reales).

Si queremos la circunferencia exacta o área de un círculo, dejamos el símbolo en la respuesta. Podemos obtener una respuesta aproximada sustituyendo como el valor de Utilizamos el símbolo para mostrar que el resultado es aproximado, no exacto.

Propiedades de Circles

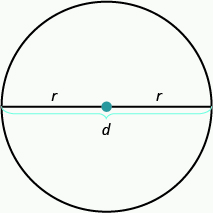
Dado que el diámetro es el doble del radio, otra forma de encontrar la circunferencia es usar la fórmula

Supongamos que queremos encontrar el área exacta de un círculo de pulgadas de radio. Para calcular el área, evaluaríamos la fórmula para el área cuando pulgadas y dejaríamos la respuesta en términos de

Escribimos después de la Así que el valor exacto del área es pulgadas cuadradas.

Para aproximar el área, sustituiríamos

Recuerde usar unidades cuadradas, como pulgadas cuadradas, cuando calcule el área.

Esfera

Una esfera es la forma de una básquetbol, como un círculo tridimensional. Al igual que un círculo, el tamaño de una esfera está determinado por su radio, que es la distancia desde el centro de la esfera hasta cualquier punto de su superficie. Las fórmulas para el volumen y la superficie de una esfera se dan a continuación.

Mostrar de dónde vienen estas fórmulas, como hicimos para un sólido rectangular, está más allá del alcance de este curso. Nos aproximaremos\(\pi\) con 3.14.

Volumen y superficie de una esfera

Para una esfera con radio r:

Cubo o Rectángulo

Un cubo es un sólido rectangular cuya longitud, anchura y altura son iguales. Consulte el volumen y la superficie de un cubo, a continuación. Sustituyendo, s por el largo, ancho y alto en las fórmulas para volumen y área de superficie de un sólido rectangular, obtenemos:

V=LWH S=2LH+2LW+2WH

v=s·s·s S=2s·s+2s·s+2s·s

V=s ³ S=2s ² +2s ² +2s ²

S=6S ²

Entonces, para un cubo, las fórmulas para volumen y área de superficie son V=s ³ y S=6s ².

Volumen y superficie de un cubo

Para cualquier cubo con lados de longitud s,

Cilindro

Si alguna vez has visto una lata de refresco, ya sabes cómo se ve un cilindro. Un cilindro es una figura sólida con dos círculos paralelos del mismo tamaño en la parte superior e inferior. La parte superior e inferior de un cilindro se llaman las bases. La altura h de un cilindro es la distancia entre las dos bases. Para todos los cilindros con los que trabajaremos aquí, los lados y la altura, h, serán perpendiculares a las bases.

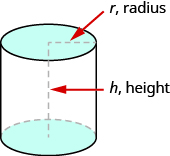
Figura #. Un cilindro tiene dos bases circulares de igual tamaño. La altura es la distancia entre las bases.

Los sólidos rectangulares y los cilindros son algo similares porque ambos tienen dos bases y una altura. La fórmula para el volumen de un sólido rectangular, V=Bh, también se puede utilizar para encontrar el volumen de un cilindro.

Para el sólido rectangular, el área de la base, B, es el área de la base rectangular, largo × ancho. Para un cilindro, el área de la base, B, es el área de su base circular, πr ². La siguiente figura compara cómo se utiliza la fórmula V=Bh para sólidos rectangulares y cilindros.

Ver cómo un cilindro es similar a un sólido rectangular puede facilitar la comprensión de la fórmula para el volumen de un cilindro.

Para entender la fórmula para la superficie de un cilindro, piense en una lata de verduras. Tiene tres superficies: la parte superior, la inferior y la pieza que forma los lados de la lata. Si cortas cuidadosamente la etiqueta del costado de la lata y la desenrollas, verás que es un rectángulo. Consulte la figura a continuación.

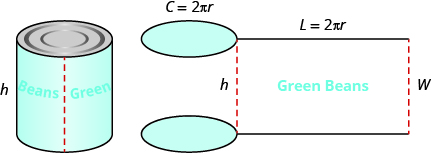
Al cortar y desenrollar la etiqueta de una lata de verduras, podemos ver que la superficie de un cilindro es un rectángulo. La longitud del rectángulo es la circunferencia de la base del cilindro, y el ancho es la altura del cilindro.

La distancia alrededor del borde de la lata es la circunferencia de la base del cilindro y también es la longitud L de la etiqueta rectangular. La altura del cilindro es el ancho W de la etiqueta rectangular. Así que el área de la etiqueta se puede representar como

Para encontrar la superficie total del cilindro, agregamos las áreas de los dos círculos al área del rectángulo.

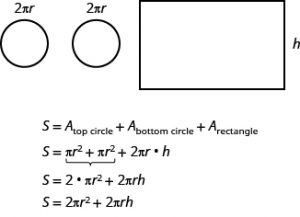
El área superficial de un cilindro con radio r y altura h, es S=2πR ² +2πrh

Volumen y superficie de un cilindro

Para un cilindro con radio r y altura h:

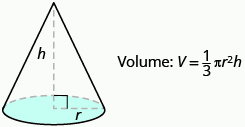
Cono

La primera imagen que muchos de nosotros tenemos cuando escuchamos la palabra 'cono' es un cono de helado. Hay muchas otras aplicaciones de los conos (pero la mayoría no son tan sabrosos como los conos de helado). En esta sección, veremos cómo encontrar el volumen de un cono.

En geometría, un cono es una figura sólida con una base circular y un vértice. La altura de un cono es la distancia entre su base y el vértice.Los conos que veremos en esta sección siempre tendrán la altura perpendicular a la base. Consulte la figura a continuación.

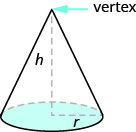
La altura de un cono es la distancia entre su base y el vértice.

Anteriormente en esta sección, vimos que el volumen de un cilindro es V=πR ² h Podemos pensar en un cono como parte de un cilindro. La siguiente figura muestra un cono colocado dentro de un cilindro con la misma altura y la misma base. Si comparamos el volumen del cono y el cilindro, podemos ver que el volumen del cono es menor que el del cilindro.

El volumen de un cono es menor que el volumen de un cilindro con la misma base y altura.

De hecho, el volumen de un cono es exactamente un tercio del volumen de un cilindro con la misma base y altura. El volumen de un cono es

Dado que la base de un cono es un círculo, podemos sustituir la fórmula de área de un círculo, πr ², por B para obtener la fórmula para volumen de un cono.

Volumen de un Cono

Para un cono con radio r y altura h.

Tablas de conversión de pesos y medidas

Medida Líquida

8 onzas = 1 taza

2 tazas= 1 pinta

16 onzas= 1 pinta

4 tazas= 1 cuarto de galón

2 pintas= 1 cuarto de galón

4 cuartos= 1 galón

3 cucharaditas= 1 cucharada

2 cdas= 1/8 taza o 1 onza líquida

4 cucharadas= 1/4 taza

8 cucharadas= 1/2 taza

1 cucharadita= 60 gotas

Conversión de medidas de líquidos estadounidenses a sistema métrico

1 onza fluido= 29.573 mililitros

1 taza= 230 mililitros

1 cuarto= .94635 litros

.033814 onzas fluidas= 1 mililitro

3.3814 onzas fluidas= 1 decilitro

33.814 onzas líquidas o 1.0567 cuartos= 1 litro

Medida Seca

2 pintas= 1 cuarto de galón

4 cuartos= 1 galón

8 cuartos= 2 galones o 1 picoteo

4 picota= 8 galones o 1 bushel

16 onzas= 1 libra

2000 libras= 1 tonelada

Conversión de peso y masa estadounidenses a sistema métrico

.0353 onzas= 1 gramo

1/4 onza= 7 gramos

1 onza= 28.35 gramos

4 onzas= 113.4 gramos

8 onzas= 226.8 gramos

1 libra= 454 gramos

2.2046 libras= 1 kilogramo

1.1023 toneladas cortas= 1 tonelada métrica

Medida Lineal

12 pulgadas= 1 pie

3 pies= 1 yarda

5.5 yardas= 1 varilla

40 varas= 1 furlong

8 furlongs (5280 pies) = 1 milla

6080 pies= 1 milla náutica

Conversión de medidas lineales estadounidenses a sistema métrico

1 pulgada= 2.54 centímetros

1 pie= .3048 metros

1 yard= .9144 metros

1 milla= 1609.3 metros o 1.6093 kilómetros

.03937 pulgadas= 1 milímetro

.3937 pulgadas= 1 centímetro

3.937 pulgadas= 1 decímetro

39.37 pulgadas= 1 metro

3280.8 pies o .62137 millas= 1 kilómetro

Temperatura

Para convertir Fahrenheit a Centígrados: Restar 32, Multiplicar por 5, luego Dividir por 9

Para convertir Centígrados a Fahrenheit: Multiplicar por 9, Dividir por 5, luego Agregar 32