1.2: Visualización

Ahora que has aprendido sobre los tipos de líneas que se encuentran en las impresiones, el siguiente paso es desarrollar tus habilidades de visualización. La capacidad de” ver” dibujos técnicos; es decir, de” pensar en tres dimensiones”, es la parte más importante de este curso. Dado que la mayoría de las impresiones de ingeniería y arquitectura utilizan alguna forma de proyección ortográfica (dibujo multivista), se enfatizará ese tipo de dibujo.

Antes de entrar en un estudio de proyección ortográfica, debe ser capaz de reconocer varios otros tipos de dibujos. Ellos son; 1. Dibujo en perspectiva, 2. Dibujo oblicuo, y 3. Dibujo isométrico. En grupo, se les llama “dibujos pictóricos”. Se encuentran en las impresiones y son fáciles de visualizar, así que veamos sus diferencias.

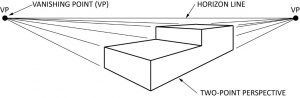
Perspectiva

La perspectiva es la forma más realista de dibujar. Los artistas utilizan la perspectiva de un punto, dos puntos (se muestran aquí) y tres puntos para crear profundidad visual. Las perspectivas son utilizadas por arquitectos y para pictóricas industriales de planos, maquinaria y otros temas donde se requiere realismo. Los objetos dibujados en perspectiva se hacen más pequeños a medida que retroceden hacia el horizonte.

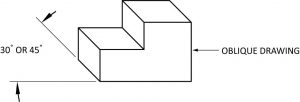
Oblicua

Los dibujos oblicuos se dibujan con un plano (frontal) del objeto paralelo a la superficie de dibujo. El lado u otra parte visible del objeto se dibuja generalmente a 30◦ o 45◦. Tenga en cuenta que solo el lado está en ángulo. Muchas veces estos tipos de dibujo no se dibujan a escala. Las líneas que retroceden se dibujan a 45◦ o 30◦ y se dibujarán a una escala diferente a la de las líneas verticales y horizontales. Esto hace que el dibujo parezca “fuera de forma”. Este tipo de dibujo no se utiliza muy a menudo en la industria.

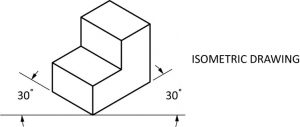
Isométrico

Los dibujos isométricos tienen menos distorsión que los dibujos oblicuos, y son utilizados con mayor frecuencia por la industria por esa razón. Un dibujo isométrico tiene ambas superficies visibles dibujadas a 30◦. Estos son los tipos de dibujos más utilizados en la industria de tuberías y requieren mucha práctica para comprender completamente cómo dibujar. Ellos representan mejor lo que se está construyendo y cómo se verá desde los diferentes lados con un solo dibujo.

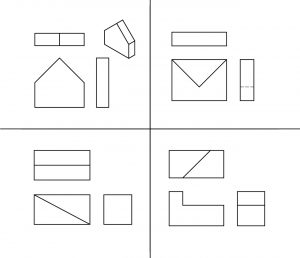
Direcciones: Nombra los tipos de dibujos que se muestran a continuación. Consulta tus propias respuestas.

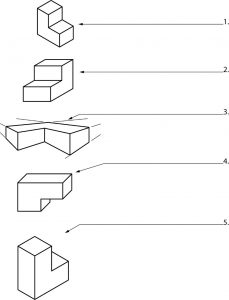
Vista Individual

Una sola vista de un objeto es a veces todo lo que se necesita para una explicación visual completa. Cuando se incluyen dimensiones, material y otra información, un objeto que requiere una sola vista es fácil de entender.

La mayoría de los dibujos de una vista son de objetos planos, hechos de materiales como chapa metálica y material de juntas. Los objetos esféricos, como una bala de cañón, requerirían solo una vista y una nota que indicara el material y el diámetro de la esfera.

El objeto que se muestra en el dibujo de una vista a continuación podría estar hecho de cualquier material apropiado que pudiera especificarse. En apariencia, es muy parecido a la junta utilizada como parte del sistema de enfriamiento en muchos autos. Todo lo que habría que destacar es el tipo de material y grosor requeridos.

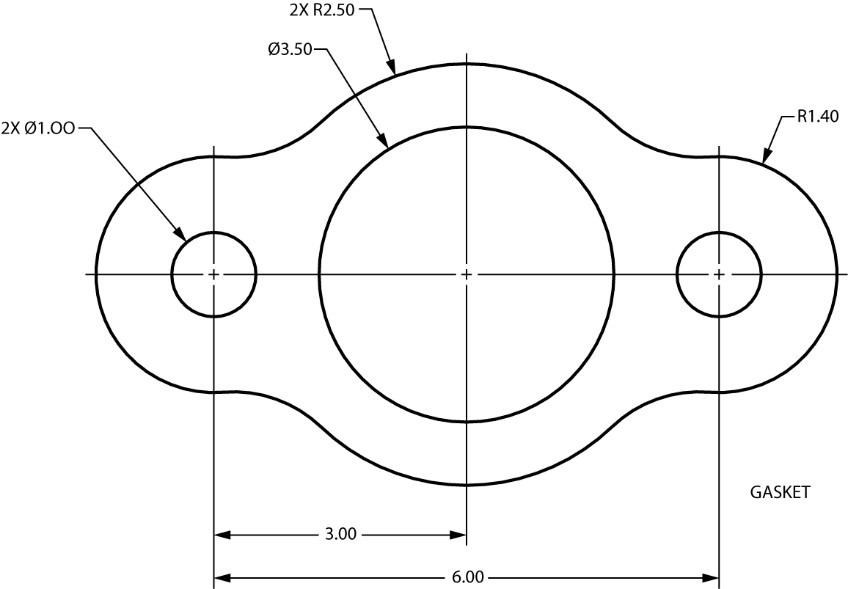
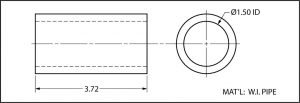
Dos Vistas

En ocasiones, los dibujos de “dos vistas” se utilizan en las impresiones. Dos vistas pueden ser todo lo que se necesita para mostrar la forma de un objeto. Los objetos que son cilíndricos, como una longitud de tubería, generalmente se muestran en una impresión con dos vistas. En tal caso, dos puntos de vista son suficientes para explicar la forma. Observe en el dibujo de dos vistas que se muestra a continuación que la longitud de la tubería se muestra en una vista, mientras que el diámetro se llama en la otra. Sin la opinión de la derecha, ¿con qué podría confundirse esta forma? Tubo cuadrado, canal...

Proyección Ortográfica

La proyección ortográfica es un nombre dado a dibujos que suelen tener tres vistas. A menudo, las tres vistas seleccionadas son la parte superior, frontal y derecha. Es posible, por supuesto, seleccionar otras vistas como el lado izquierdo o inferior. Generalmente, sin embargo, es la parte superior, frontal y derecha que tradicionalmente ven la persona que lee las impresiones.

Dado que la mayoría de las impresiones hacen uso del sistema de proyección ortográfica, y debido a que las vistas superior, frontal, lateral derecha se usan con mayor frecuencia, es importante que tengas su orden, o disposición en la impresión fija en tu mente. Para ayudarte a entender este sistema, piensa en un borrador de pizarra, una longitud corta de madera de 2″ x 4″ o un ladrillo común. Se ve así:

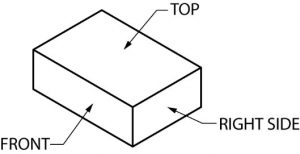
Cuando se ve en una impresión, utilizando proyección ortográfica, aparecería así.

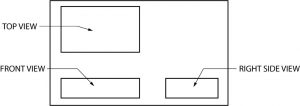
Este sistema de proyección ortográfica puede ser difícil de entender o visualizar al principio, pero lo agarrarás con algo de práctica. Aquí hay un ejemplo básico de cómo funciona, usando un objeto simple.

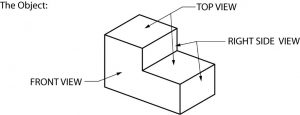
La proyección ortográfica no muestra profundidad, por lo que el objeto mostrado arriba aparecerá plano. Con la práctica, sin embargo, aprenderás a escanear las tres vistas y a “leer” en profundidad en ellas. Recuerda que la ubicación de las vistas superior, frontal y lateral derecha no cambia. Las líneas de proyección entre las vistas ortográficas a continuación muestran la relación de altura, anchura y profundidad que existe entre cada vista y las otras dos vistas.

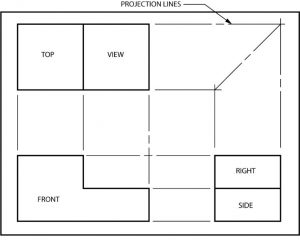
En caso de que no entendieras las tres vistas en la última página, echemos otro vistazo a lo mismo. Estos números de tiempo se utilizarán para la identificación de las superficies.

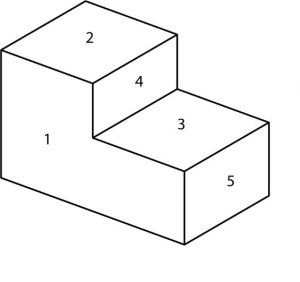
Usando proyección ortográfica, el objeto con las superficies numeradas aparece así:

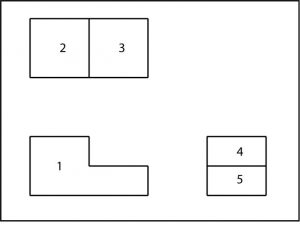
Observe que la vista frontal (1) es la clave del dibujo, ya que muestra más claramente la forma del objeto. Te dice que el objeto tiene forma de “L” desde el frente. Los otros dos puntos de vista no te dicen mucho por sí mismos. Al mirar la superficie 1, sin embargo, se puede ver que 2 es más alto que 3. Por lo tanto, al “leer” las superficies, 2 debería parecer estar más cerca de ti que 3. Ahora mira 4 y 5. ¿Qué superficie se proyecta más cerca de ti? ·

Respuesta: Superficie 5 (rotar y colocar en la parte inferior del diseño)

Ahora dibuje una caja simple y pegue todos los lados juntos para formar un cubo. El cubo será de 2” x 2” x 2”. Una vez que el instructor haya aprobado su dibujo, procederá a cortar y pegar los bordes juntos para formar un cubo.

Cuestionario de visualización

Direcciones:

Todas las superficies visibles de los objetos mostrados están numeradas. Para completar este cuestionario, debes colocar esos números en las superficies correspondientes de los dibujos ortográficos.

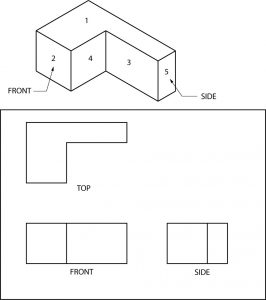
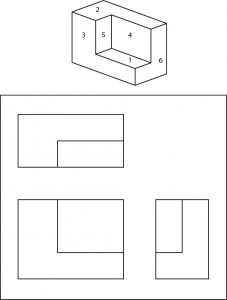
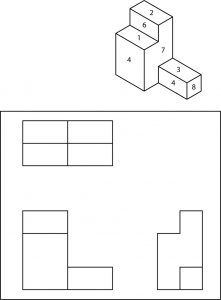
Quizás te estés preguntando en este punto por qué algo así como la proyección ortográfica se usa en las impresiones cuando los dibujos isométricos u oblicuos son mucho más fáciles de visualizar. La respuesta es que ambos tipos de pictóricos se utilizan para dibujos relativamente sencillos. Sin embargo, cuando un objeto es complejo, ninguno puede igualar el sistema ortográfico para una presentación clara de dimensiones, notas y detalles de configuración.

Superficies Ocultas

Otra ventaja de la proyección ortográfica es que permite que la persona que lee la impresión tenga la capacidad de ver el interior, o superficies de un objeto que normalmente no se podía ver.

Con objetos complicados esto puede llegar a ser muy útil.

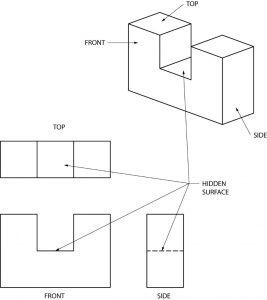
En el dibujo de abajo, la línea oculta en la vista lateral derecha representa toda la superficie del área plana entre los dos lados superiores.

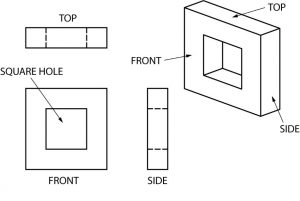
En este ejemplo, las líneas ocultas resultan de un agujero cuadrado que atraviesa el centro del objeto.

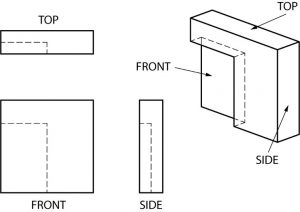
Las líneas ocultas en este ejemplo están ahí porque una parte de una esquina de la superficie frontal fue cortada, o “empotrada.

Superficies Ocultas

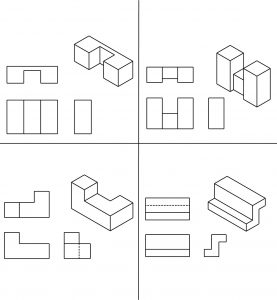
Direcciones: Dibuja las líneas ocultas que faltan en las vistas a continuación. Cada problema tiene una visión incompleta.

Superficies Curvas

Las superficies curvas son quizás difíciles de “ver” hasta que recuerdes que la curva solo se muestra en una vista. Debes poner la curva en las otras vistas tú mismo, a través de la visualización. Intenta pensar que cuando hay un cambio brusco de dirección como en una esquina, entonces eso producirá una línea visible en otra vista. Cuando el cambio de dirección es suave como una curva, no se verá ninguna línea.

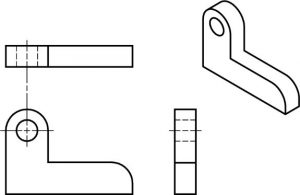
Aquí hay otro ejemplo de superficies curvas:

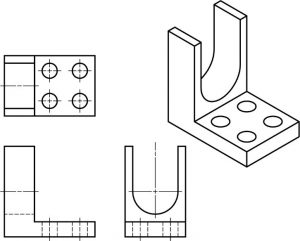
Ejercicio de superficies curvas.

Direcciones: Dibuja las líneas que faltan en las vistas a continuación. Cada problema tiene una visión incompleta. No dibujar líneas centrales.

Superficies inclinadas

Las superficies inclinadas son aquellas que están en ángulo o inclinadas. Es decir, son superficies que no son ni horizontales ni verticales. En la visualización de dibujos ortográficos es necesario estar alerta a los ángulos y superficies inclinadas, ya que a menudo se encuentran en las impresiones que leerás más adelante.

Observe la línea oculta en la vista derecha creada por la superficie inclinada en este objeto:

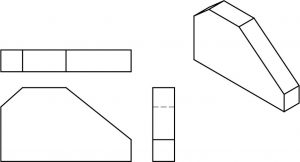
Aquí hay un objeto con dos superficies inclinadas.

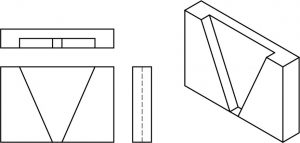
Ejercicio de superficies inclinadas

Direcciones: Dibuja las líneas que faltan en las vistas a continuación. Cada problema tiene una visión incompleta.