2.2: Física cuántica
- Page ID
- 153716
“Creo que es seguro decir que nadie entiende la mecánica cuántica”.
—Físico Richard P. Feynman
Decir que la invención de los dispositivos semiconductores fue una revolución no sería una exageración. Esto no sólo fue un logro tecnológico impresionante, sino que allanó el camino para desarrollos que alterarían indeleblemente a la sociedad moderna. Los dispositivos semiconductores hicieron posible la electrónica miniaturizada, incluyendo computadoras, ciertos tipos de equipos médicos de diagnóstico y tratamiento, y dispositivos de telecomunicaciones populares, por nombrar algunas aplicaciones de esta tecnología.
Pero detrás de esta revolución en la tecnología se alza una revolución aún mayor en la ciencia general: el campo de la física cuántica. Sin este salto en la comprensión del mundo natural, el desarrollo de dispositivos semiconductores (y dispositivos electrónicos más avanzados aún en desarrollo) nunca habría sido posible. La física cuántica es un reino de la ciencia increíblemente complicado. Este capítulo no es más que una breve descripción general. Cuando los científicos del calibre de Feynman dicen que “nadie lo entiende”, puedes estar seguro de que es un tema complejo. Sin una comprensión básica de la física cuántica, o al menos una comprensión de los descubrimientos científicos que llevaron a su formulación, sin embargo, es imposible entender cómo y por qué funcionan los dispositivos electrónicos semiconductores. La mayoría de los libros de texto introductorios de electrónica que he leído intentan explicar los semiconductores en términos de física “clásica”, resultando en más confusión que comprensión.
Muchos de nosotros hemos visto diagramas de átomos que se parecen a la Figura a continuación.
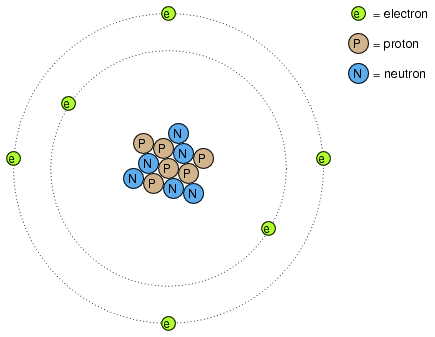
Átomo de Rutherford: electrones negativos orbitan un pequeño núcleo positivo.
Pequeñas partículas de materia llamadas protones y neutrones conforman el centro del átomo; los electrones orbitan como planetas alrededor de una estrella. El núcleo lleva una carga eléctrica positiva, debido a la presencia de protones (los neutrones no tienen carga eléctrica alguna), mientras que la carga negativa de equilibrio del átomo reside en los electrones orbitantes. Los electrones negativos son atraídos por los protones positivos así como los planetas son atraídos gravitacionalmente por el Sol, sin embargo, las órbitas son estables debido al movimiento de los electrones. Este modelo popular del átomo se debe a la obra de Ernest Rutherford, quien alrededor del año 1911 determinó experimentalmente que las cargas positivas de los átomos se concentraban en un núcleo minúsculo y denso en lugar de distribuirse uniformemente alrededor del diámetro como lo propuso un investigador anterior, J.J. Thompson.
El experimento de dispersión de Rutherford consistió en bombardear una fina lámina de oro con partículas alfa cargadas positivamente como en la Figura siguiente. Los jóvenes egresados H. Geiger y E. Marsden experimentaron resultados inesperados. Algunas partículas Alfa fueron desviadas en grandes ángulos. Algunas partículas Alfa se retrodispersaron, retrocediendo a casi 180 o. La mayoría de las partículas pasaron a través de la lámina de oro sin desviar, lo que indica que la lámina era en su mayoría espacio vacío. El hecho de que unas pocas partículas alfa experimentaran grandes deflexiones indicó la presencia de un minúsculo núcleo cargado positivamente.
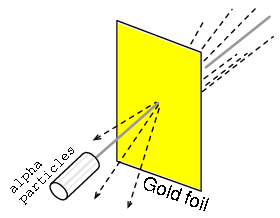
Dispersión de Rutherford: un haz de partículas alfa es dispersado por una delgada lámina de oro.
Aunque el modelo atómico de Rutherford representó los datos experimentales mejor que el de Thompson, todavía no era perfecto. Se emprendieron otros intentos de definir la estructura atómica, y estos esfuerzos ayudaron a allanar el camino para los extraños descubrimientos de la física cuántica. Hoy nuestra comprensión del átomo es bastante más compleja. Sin embargo, a pesar de la revolución de la física cuántica y su contribución a nuestra comprensión de la estructura atómica, la imagen del átomo del sistema solar de Rutherford se incrustó en la conciencia popular hasta tal punto que persiste en algunas áreas de estudio incluso cuando no es apropiado.
Considera esta breve descripción de los electrones en un átomo, tomada de un popular libro de texto electrónico:
Por lo tanto, los electrones negativos orbitantes son atraídos hacia el núcleo positivo, lo que nos lleva a la pregunta de por qué los electrones no vuelan hacia el núcleo del átomo. La respuesta es que los electrones orbitantes permanecen en su órbita estable debido a dos fuerzas iguales pero opuestas. La fuerza centrífuga hacia afuera ejercida sobre los electrones debido a la órbita contrarresta la fuerza interna atractiva (centrípeta) que intenta tirar de los electrones hacia el núcleo debido a las cargas diferentes.
De acuerdo con el modelo de Rutherford, este autor proyecta los electrones como trozos sólidos de materia comprometidos en órbitas circulares, su atracción hacia el núcleo de carga opuestamente equilibrada por su movimiento. La referencia a la “fuerza centrífuga” es técnicamente incorrecta (incluso para planetas orbitantes), pero es fácilmente perdonado por su aceptación popular: en realidad, no existe tal cosa como una fuerza que empuje a cualquier cuerpo orbitante lejos de su centro de órbita. Parece así porque la inercia de un cuerpo tiende a mantenerlo viajando en línea recta, y como una órbita es una desviación constante (aceleración) del recorrido en línea recta, existe una oposición inercial constante a cualquier fuerza que esté atrayendo al cuerpo hacia el centro de la órbita (centrípeta), ya sea gravedad, atracción electrostática, o incluso la tensión de un enlace mecánico.
El verdadero problema de esta explicación, sin embargo, es la idea de que los electrones viajen en órbitas circulares en primer lugar. Es un hecho verificable que las cargas eléctricas aceleradas emiten radiación electromagnética, y este hecho se conoció incluso en la época de Rutherford. Dado que el movimiento en órbita es una forma de aceleración (el objeto orbitante en aceleración constante lejos del movimiento normal en línea recta), los electrones en un estado orbitante deberían estar arrojando radiación como lodo de una llanta giratoria. Se sabe que los electrones acelerados alrededor de trayectorias circulares en aceleradores de partículas llamados sincrotrones hacen esto, y el resultado se llama radiación sincrotrón. Si los electrones perdieran energía de esta manera, sus órbitas eventualmente se desintegrarían, resultando en colisiones con el núcleo cargado positivamente. Sin embargo, esto no suele suceder dentro de los átomos. De hecho, las “órbitas” de electrones son notablemente estables en una amplia gama de condiciones.
Además, los experimentos con átomos “excitados” demostraron que la energía electromagnética emitida por un átomo solo ocurre a ciertas frecuencias definidas. Se sabe que los átomos que son “excitados” por influencias externas como la luz absorben esa energía y la devuelven como ondas electromagnéticas de frecuencias específicas, como un diapasón que suena a un tono fijo sin importar cómo se golpee. Cuando la luz emitida por un átomo excitado es dividida en sus frecuencias constituyentes (colores) por un prisma, aparecen distintas líneas de color en el espectro, siendo el patrón de líneas espectrales único para ese elemento. Este fenómeno es comúnmente utilizado para identificar elementos atómicos, e incluso medir las proporciones de cada elemento en un compuesto o mezcla química. Según el modelo atómico del sistema solar de Rutherford (considerando los electrones como trozos de materia libres para orbitar en cualquier radio) y las leyes de la física clásica, los átomos excitados deberían devolver energía en un rango de frecuencias prácticamente ilimitado en lugar de unos pocos seleccionados. En otras palabras, si el modelo de Rutherford fuera correcto, no habría efecto de “diapasón”, y el espectro de luz emitido por cualquier átomo aparecería como una banda continua de colores en lugar de como unas pocas líneas distintas.
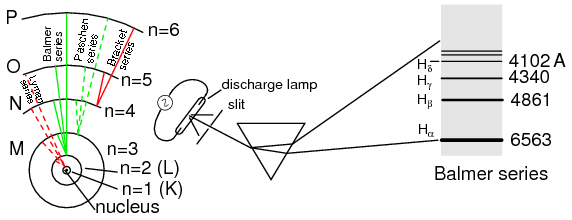
El átomo de hidrógeno de Bohr (con órbitas dibujadas a escala) solo permite que los electrones habiten orbitales discretos. Los electrones que caen de n=3,4,5, o 6 a n=2 representan la serie de líneas espectrales de Balmer.
Un investigador pionero con el nombre de Niels Bohr intentó mejorar el modelo de Rutherford después de estudiar en el laboratorio de Rutherford durante varios meses en 1912. Tratando de armonizar los hallazgos de otros físicos (sobre todo, Max Planck y Albert Einstein), Bohr sugirió que cada electrón tenía una cierta cantidad específica de energía, y que sus órbitas fueron cuantificadas de tal manera que cada uno puede ocupar ciertos lugares alrededor del núcleo, como canicas fijadas en antiguamente se imaginaba que las huellas circulares alrededor del núcleo en lugar de los satélites de alcance libre eran cada uno. (Figura anterior) En deferencia a las leyes de la electromagnetica y cargas aceleradoras, Bohr aludió a estas “órbitas” como estados estacionarios para escapar de la implicación de que estaban en movimiento.
Si bien el ambicioso intento de Bohr de reenmarcar la estructura del átomo en términos que coincidieron más cerca de los resultados experimentales fue un hito en la física, no fue completo. Su análisis matemático produjo mejores predicciones de eventos experimentales que los análisis pertenecientes a modelos anteriores, pero aún quedaban algunas preguntas sin respuesta sobre por qué los electrones deberían comportarse de formas tan extrañas. La afirmación de que los electrones existían en estados estacionarios cuantificados alrededor del núcleo representaba datos experimentales mejor que el modelo de Rutherford, pero no tenía idea de qué obligaría a los electrones a manifestar esos estados particulares. La respuesta a esa pregunta tenía que provenir de otro físico, Louis de Broglie, aproximadamente una década después.
De Broglie propuso que los electrones, como fotones (partículas de luz) manifestaron propiedades similares a partículas y onduladas. Partiendo de esta propuesta, sugirió que un análisis de los electrones orbitantes desde una perspectiva de onda en lugar de una perspectiva de partículas podría tener más sentido de su naturaleza cuantificada. En efecto, se alcanzó otro avance en la comprensión.
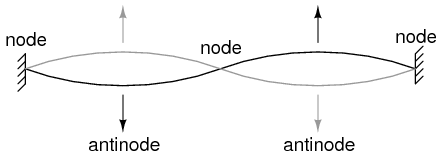
La cuerda que vibra a frecuencia resonante entre dos puntos fijos forma onda estacionaria.
El átomo según de Broglie consistía en electrones existentes como ondas estacionarias, fenómeno bien conocido por los físicos en una variedad de formas. Como la cuerda arrancada de un instrumento musical (Figura anterior) vibrando a una frecuencia resonante, con “nodos” y “antinodos” en posiciones estables a lo largo de su longitud. De Broglie imaginó electrones alrededor de átomos parados como ondas dobladas alrededor de un círculo como en la Figura siguiente.

Electrón “orbitando” como onda estacionaria alrededor del núcleo, (a) dos ciclos por órbita, (b) tres ciclos por órbita.
Los electrones sólo podían existir en ciertas “órbitas” definidas alrededor del núcleo porque esas eran las únicas distancias donde termina la onda coincidirían. En cualquier otro radio, la onda debería interferir destructivamente consigo misma y así dejar de existir.
La hipótesis de De Broglie dio tanto soporte matemático como una analogía física conveniente para dar cuenta de los estados cuantificados de los electrones dentro de un átomo, pero su modelo atómico aún estaba incompleto. En pocos años, sin embargo, los físicos Werner Heisenberg y Erwin Schrodinger, trabajando independientemente unos de otros, construyeron sobre el concepto de de Broglie de una dualidad de onda de materia para crear modelos matemáticamente más rigurosos de partículas subatómicas.
A este avance teórico del modelo primitivo de onda estacionaria de Broglie a la matriz de Heisenberg y a los modelos de ecuaciones diferenciales de Schrodinger se le dio el nombre de mecánica cuántica, e introdujo una característica bastante impactante en el mundo de las partículas subatómicas: el rasgo de probabilidad, o incertidumbre. Según la nueva teoría cuántica, era imposible determinar la posición exacta y el momento exacto de una partícula al mismo tiempo. La explicación popular de este “principio de incertidumbre” fue que se trataba de un error de medición (es decir, al intentar medir con precisión la posición de un electrón, interfieres con su impulso y así no puedes saber qué era antes de que se tomara la medición de posición, y viceversa). La sorprendente implicación de la mecánica cuántica es que las partículas en realidad no tienen posiciones y momentos precisos, sino que equilibran las dos cantidades de tal manera que sus incertidumbres combinadas nunca disminuyen por debajo de un cierto valor mínimo.
Esta forma de relación de “incertidumbre” existe en áreas distintas a la mecánica cuántica. Como se discutió en el capítulo “Señales de CA de Frecuencia Mixta” en el volumen II de esta serie de libros, existe una relación mutuamente excluyente entre la certeza de los datos de dominio de tiempo de una forma de onda y sus datos de dominio de frecuencia. En términos simples, cuanto más precisamente conocemos su (s) frecuencia (es) constituyente (s), menos precisamente conocemos su amplitud en el tiempo, y viceversa. Para citarme:
Una forma de onda de duración infinita (número infinito de ciclos) se puede analizar con absoluta precisión, pero cuantos menos ciclos disponga la computadora para su análisis, menos preciso será el análisis. Cuantas menos veces circule una onda, menos segura es su frecuencia. Llevando este concepto a su extremo lógico, un pulso corto, una forma de onda que ni siquiera completa un ciclo, en realidad no tiene frecuencia, sino que actúa como un rango infinito de frecuencias. Este principio es común a todos los fenómenos basados en ondas, no solo a las tensiones y corrientes de CA.
Para determinar con precisión la amplitud de una señal variable, debemos muestrearla en un lapso de tiempo muy estrecho. Sin embargo, hacer esto limita nuestra visión de la frecuencia de la onda. Por el contrario, para determinar la frecuencia de una onda con gran precisión, debemos muestrearla a lo largo de muchos ciclos, lo que significa que perdemos la visión de su amplitud en un momento dado. Por lo tanto, no podemos conocer simultáneamente la amplitud instantánea y la frecuencia general de cualquier onda con precisión ilimitada. Más extraño aún, esta incertidumbre es mucho más que la imprecisión del observador; reside en la naturaleza misma de la ola. No es como si fuera posible, dada la tecnología adecuada, obtener mediciones precisas tanto de amplitud como de frecuencia instantáneas a la vez. Literalmente, una onda no puede tener tanto una amplitud precisa e instantánea, como una frecuencia precisa al mismo tiempo.
La incertidumbre mínima de la posición y el impulso de una partícula expresada por Heisenberg y Schrodinger no tiene nada que ver con la limitación en la medición; más bien es una propiedad intrínseca de la naturaleza dual de la partícula de onda de materia. Los electrones, por lo tanto, no existen realmente en sus “órbitas” como bits de materia definidos con precisión, o incluso como formas de onda definidas con precisión, sino más bien como “nubes” —el término técnico es ondafunción — de distribución de probabilidad, como si cada electrón estuviera “esparcido” o “manchado” en un rango de posiciones y momenta.
Esta visión radical de los electrones como nubes imprecisas al principio parece contradecir al principio original de los estados de electrones cuantificados: que los electrones existen en “órbitas” discretas y definidas alrededor de los núcleos atómicos. Fue, después de todo, este descubrimiento el que llevó a la formación de la teoría cuántica para explicarlo. Qué extraño parece que una teoría desarrollada para explicar el comportamiento discreto de los electrones termine declarando que los electrones existen como “nubes” más que como piezas discretas de materia. Sin embargo, el comportamiento cuantificado de los electrones no depende de que los electrones tengan valores definidos de posición e impulso, sino de otras propiedades llamadas números cuánticos. En esencia, la mecánica cuántica prescinde de las nociones comúnmente sostenidas de posición absoluta e impulso absoluto, y las reemplaza con nociones absolutas de una especie que no tiene análogos en la experiencia común.
Aunque se sabe que los electrones existen en formas etéreas, “como nubes” de probabilidad distribuida en lugar de como trozos discretos de materia, esas “nubes” tienen otras características que son discretas. Cualquier electrón en un átomo puede describirse mediante cuatro medidas numéricas (los números cuánticos mencionados anteriormente), llamadas números Principal, Momentum Angular, Magnético y Spin. A continuación se presenta una sinopsis de los significados de cada uno de estos números:
Número cuántico principal: Simbolizado por la letra n, este número describe la concha en la que reside un electrón. Una “capa” de electrones es una región del espacio alrededor del núcleo de un átomo en la que se permite que existan electrones, correspondiente a los patrones estables de “onda estacionaria” de Broglie y Bohr. Los electrones pueden “saltar” de concha en concha, pero no pueden existir entre las regiones de concha.
El número cuántico principal debe ser un entero positivo (un número entero, mayor o igual a 1). En otras palabras, el número cuántico principal para un electrón no puede ser 1/2 o -3. Estos valores enteros no se alcanzaron arbitrariamente, sino a través de evidencias experimentales de espectros de luz: las diferentes frecuencias (colores) de la luz emitida por los átomos de hidrógeno excitados siguen una secuencia matemáticamente dependiente de valores enteros específicos como se ilustra en la Figura anterior.
Cada caparazón tiene la capacidad de contener múltiples electrones. Una analogía para las conchas de electrones son las filas concéntricas de asientos de un anfiteatro. Así como una persona sentada en un anfiteatro debe elegir una fila para sentarse (uno no puede sentarse entre filas), los electrones deben “elegir” un caparazón en particular para “sentarse” en. Al igual que en las filas de anfiteatro, las conchas más externas contienen más electrones que las conchas internas. Además, los electrones tienden a buscar el caparazón más bajo disponible, ya que las personas en un anfiteatro buscan el asiento más cercano al centro del escenario. Cuanto mayor sea el número de caparazón, mayor será la energía de los electrones que contiene.
El número máximo de electrones que puede contener cualquier caparazón se describe mediante la ecuación 2n 2, donde “n” es el número cuántico principal. Así, el primer caparazón (n=1) puede contener 2 electrones; el segundo caparazón (n=2) 8 electrones, y el tercer caparazón (n=3) 18 electrones. (Figura abajo)
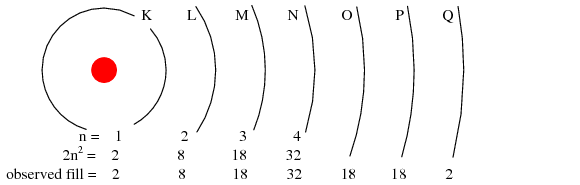
Número cuántico principal n y número máximo de electrones por caparazón ambos predichos por 2 (n 2), y observados. Orbitales no a escala.
Las conchas de electrones en un átomo se designaban anteriormente por letra en lugar de por número. El primer caparazón (n=1) se etiquetó K, el segundo caparazón (n=2) L, el tercer caparazón (n=3) M, el cuarto caparazón (n=4) N, el quinto caparazón (n=5) O, el sexto caparazón (n=6) P y el séptimo caparazón (n=7) Q.
Número Cuántico de Momentum Angular: Un proyectil, está compuesto por subconchas. Uno podría inclinarse a pensar en las subconchas como simples subdivisiones de conchas, como carriles que dividen una carretera. Las subconchas son mucho más extrañas. Las subconchas son regiones del espacio donde se permite que existan “nubes” de electrones, y diferentes subconchas en realidad tienen diferentes formas. La primera subcapa tiene forma de esfera, (Figura abajo (s)) que tiene sentido cuando se visualiza como una nube de electrones que rodea el núcleo atómico en tres dimensiones. La segunda subcapa, sin embargo, se asemeja a una mancuerna, compuesta por dos “lóbulos” unidos en un solo punto cerca del centro del átomo. (Figura abajo (p)) La tercera subcapa típicamente se asemeja a un conjunto de cuatro “lóbulos” agrupados alrededor del núcleo del átomo. Estas formas de subshell recuerdan a representaciones gráficas de la intensidad de la señal de la antena de radio, con regiones bulbosas en forma de lóbulo que se extienden desde la antena en varias direcciones. (Figura a continuación (d))
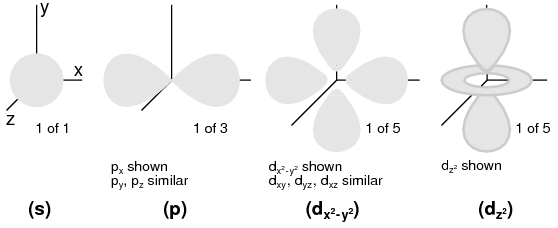
Orbitales: (s) Simetría triple. (p) Se muestra: p x, una de las tres orientaciones posibles (p x, p y, p z), alrededor de sus respectivos ejes. (d) Se muestra: d x 2 - y 2 similar a d xy, d yz, d xz. Se muestra: d z 2. Posibles orientaciones orbitales d: cinco.
Los números cuánticos de momento angular válidos son enteros positivos como los números cuánticos principales, pero también incluyen cero. Estos números cuánticos para electrones están simbolizados por la letra l. El número de subshells en un shell es igual al número cuántico principal del shell. Así, el primer shell (n=1) tiene un subshell, numerado 0; el segundo shell (n=2) tiene dos subshells, numerados 0 y 1; el tercer shell (n=3) tiene tres subshells, numerados 0, 1 y 2.
Una convención más antigua para la descripción de subshell usaba letras en lugar de números. En esta notación, el primer subshell (l=0) fue designado s, el segundo subshell (l=1) designado p, el tercer subshell (l=2) designado d, y el cuarto subshell (l=3) designado f. Las letras provienen de las palabras agudo, principal (que no debe confundirse con el número cuántico principal, n), difuso y fundamental. Seguirá viendo esta convención notacional en muchas tablas periódicas, utilizadas para designar la configuración electrónica de las conchas más externas, o de valencia, de los átomos. (Figura abajo)
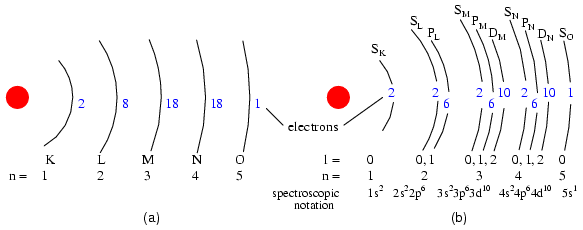
(a) Representación de Bohr del átomo de Plata, (b) Subshell Representación de Ag con división de conchas en subconchas (número cuántico angular l). Este diagrama no implica nada sobre la posición real de los electrones, sino que representa los niveles de energía.
Número cuántico magnético: El número cuántico magnético para un electrón clasifica qué orientación es puntiaguda su forma de subcapa. Los “lóbulos” de los subproyectiles apuntan en múltiples direcciones. Estas diferentes orientaciones se llaman orbitales. Para la primera subcapa (s; l=0), que se asemeja a una esfera que apunta en ninguna “dirección”, por lo que solo hay una orbital. Para el segundo subshell (p; l=1) en cada caparazón, que se asemeja al punto de mancuernas en tres direcciones posibles. Piense en tres mancuernas que se cruzan en el origen, cada una orientada a lo largo de un eje diferente en un espacio de coordenadas de tres ejes.
Los valores numéricos válidos para este número cuántico consisten en números enteros que van de -l a l, y se simbolizan como m l en física atómica y l z en física nuclear. Para calcular el número de orbitales en cualquier subshell dado, doble el número de subshell y sumar 1, (2·l + 1). Por ejemplo, el primer subshell (l=0) en cualquier shell contiene un solo orbital, numerado 0; el segundo subshell (l=1) en cualquier shell contiene tres orbitales, numerados -1, 0 y 1; el tercer subshell (l=2) contiene cinco orbitales, numerados -2, -1, 0, 1 y 2; y así sucesivamente.
Al igual que los números cuánticos principales, el número cuántico magnético surgió directamente de la evidencia experimental: El efecto Zeeman, la división de líneas espectrales al exponer un gas ionizado a un campo magnético, de ahí el nombre número cuántico “magnético”.
Número cuántico de giro: Al igual que el número cuántico magnético, esta propiedad de los electrones atómicos fue descubierta a través de la experimentación. La observación cercana de las líneas espectrales reveló que cada línea era en realidad un par de líneas muy espaciadas, y se planteó la hipótesis de que esta llamada estructura fina resultaba de que cada electrón “giraba” sobre un eje como si fuera un planeta. Los electrones con diferentes “espines” emitirían frecuencias de luz ligeramente diferentes cuando se excitan. A este número cuántico se le asignó el nombre “spin”. El concepto de un electrón giratorio es ahora obsoleto, siendo más adecuado a la visión (incorrecta) de los electrones como trozos discretos de materia en lugar de como “nubes”; pero, el nombre permanece.
Los números cuánticos de espín se simbolizan como m s en física atómica y s z en física nuclear. Para cada orbital en cada subcapa en cada caparazón, puede haber dos electrones, uno con un giro de +1/2 y el otro con un giro de -1/2.
El físico Wolfgang Pauli desarrolló un principio explicando el orden de los electrones en un átomo según estos números cuánticos. Su principio, llamado el principio de exclusión Pauli, establece que no hay dos electrones en un mismo átomo que puedan ocupar exactamente los mismos estados cuánticos. Es decir, cada electrón en un átomo tiene un conjunto único de números cuánticos. Esto limita el número de electrones que pueden ocupar cualquier orbital, subcapa y caparazón dados.
Aquí se muestra la disposición de electrones para un átomo de hidrógeno:
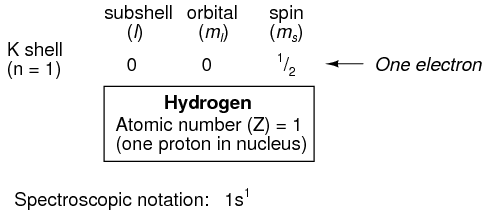
Con un protón en el núcleo, se necesita un electrón para equilibrar electrostáticamente el átomo (la carga eléctrica positiva del protón exactamente equilibrada por la carga eléctrica negativa del electrón). Este electrón reside en la capa más baja (n=1), la primera subcapa (l=0), en la única orbital (orientación espacial) de esa subcapa (m l =0), con un valor de espín de 1/2. Un método común para describir esta organización es enumerar los electrones de acuerdo con sus conchas y subcáscaras en una convención llamada notación espectroscópica. En esta notación, el número de shell se muestra como un entero, el subshell como una letra (s, p, d, f), y el número total de electrones en la subcapa (todos los orbitales, todos los espines) como un superíndice. Así, el hidrógeno, con su electrón solitario residiendo en el nivel base, se describe como 1s 1.
Pasando al siguiente átomo (en orden de número atómico), tenemos el elemento helio:
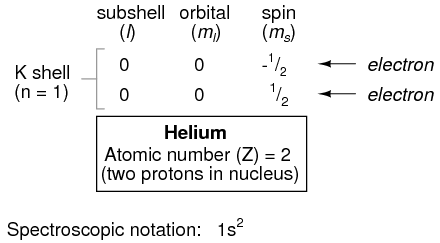
Un átomo de helio tiene dos protones en el núcleo, y esto requiere dos electrones para equilibrar la carga eléctrica doble positiva. Dado que dos electrones, uno con spin=1/2 y el otro con spin=-1/2, encajan en un orbital, la configuración electrónica del helio no requiere subconchas o conchas adicionales para contener el segundo electrón.
Sin embargo, un átomo que requiera tres o más electrones requerirá subcapas adicionales para contener todos los electrones, ya que solo dos electrones encajarán en la capa más baja (n=1). Considere el siguiente átomo en la secuencia de números atómicos crecientes, el litio:
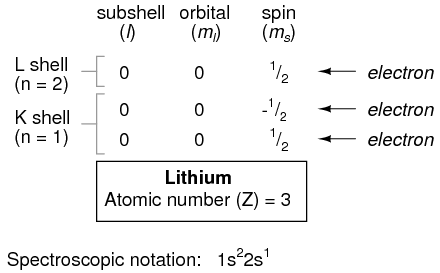
Un átomo de litio utiliza una fracción de la capacidad de la cáscara L (n=2). Esta concha en realidad tiene una capacidad total de ocho electrones (capacidad máxima de la carcasa = 2n 2 electrones). Si examinamos la organización del átomo con una capa L completamente llena, veremos cómo todas las combinaciones de subconchas, orbitales y espines están ocupadas por electrones:
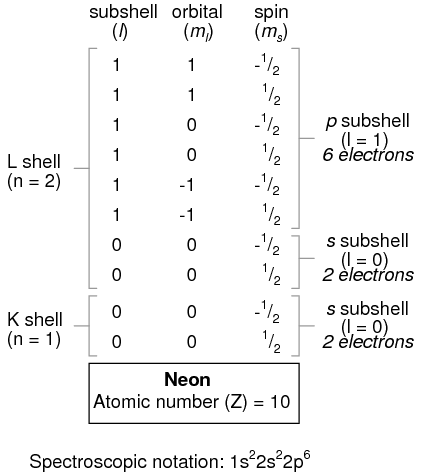
A menudo, cuando se da la notación espectroscópica para un átomo, se omiten las conchas que estén completamente llenas, y se denota la concha sin rellenar, o la concha llena de más alto nivel. Por ejemplo, el elemento neón (mostrado en la ilustración anterior), que tiene dos carcasas completamente llenas, puede describirse espectroscópicamente simplemente como 2p 6 en lugar de 1s 2 2s 2 2p 6. El litio, con su cáscara K completamente llena y un electrón solitario en la cubierta L, puede describirse simplemente como 2s 1 en lugar de 1s 2 2s 1.
La omisión de los proyectiles completamente llenos y de nivel inferior no es solo una conveniencia notacional. También ilustra un principio básico de la química: que el comportamiento químico de un elemento está determinado principalmente por sus conchas sin llenar. Tanto el hidrógeno como el litio tienen un solo electrón en sus envolturas más externas (1s 1 y 2s 1, respectivamente), dando a los dos elementos algunas propiedades similares. Ambos son altamente reactivos, y reactivos de la misma manera (uniéndose a elementos similares en modos similares). Poco importa que el litio tenga una cáscara de K completamente llena debajo de su carcasa L casi vacía: la carcasa L sin llenar es la cáscara que determina su comportamiento químico.
Los elementos que tienen carcasas exteriores completamente llenas se clasifican como nobles, y se distinguen por una no reactividad casi completa con otros elementos. Estos elementos solían clasificarse como inertes, cuando se pensaba que estos eran completamente no reactivos, pero ahora se sabe que forman compuestos con otros elementos bajo condiciones específicas.
Dado que los elementos con configuraciones electrónicas idénticas en su (s) caparazón (s) más externo (s) exhiben propiedades químicas similares, Dmitri Mendeleev organizó los diferentes elementos en una tabla en consecuencia. Tal tabla se conoce como tabla periódica de los elementos, y las tablas modernas siguen esta forma general en la Figura siguiente.
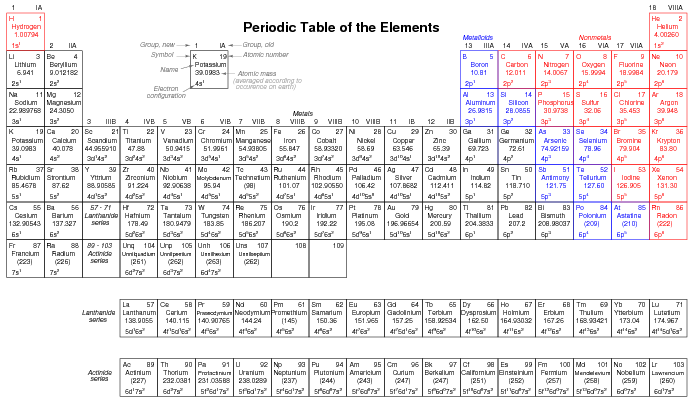
Tabla periódica de elementos químicos.
Dmitri Mendeleev, químico ruso, fue el primero en desarrollar una tabla periódica de los elementos. Si bien Mendeleev organizó su mesa según la masa atómica más que el número atómico, y produjo una tabla que no era tan útil como las tablas periódicas modernas, su desarrollo se erige como un excelente ejemplo de prueba científica. Al ver los patrones de periodicidad (propiedades químicas similares según la masa atómica), Mendeleev planteó la hipótesis de que todos los elementos deberían encajar en este esquema ordenado. Cuando descubrió manchas “vacías” en la mesa, siguió la lógica del orden existente y planteó la hipótesis de la existencia de elementos hasta ahora no descubiertos. El posterior descubrimiento de esos elementos otorgó legitimidad científica a la hipótesis de Mendeleev, fomentando futuros descubrimientos y dando lugar a la forma de la tabla periódica que usamos hoy.
Así debe funcionar la ciencia: hipótesis seguidas a sus conclusiones lógicas, y aceptadas, modificadas o rechazadas según lo determinado por la concordancia de los datos experimentales con esas conclusiones. Cualquier tonto puede formular una hipótesis después del hecho para explicar los datos experimentales existentes, y muchos lo hacen. Lo que diferencia a una hipótesis científica de la especulación post hoc es la predicción de datos experimentales futuros aún no recopilados, y la posibilidad de desprevenirlos como resultado de esos datos. Seguir audazmente una hipótesis hasta su (s) conclusión (s) lógica (s) y atreverse a predecir los resultados de futuros experimentos no es un salto dogmático de fe, sino más bien una prueba pública de esa hipótesis, abierta al desafío de cualquiera capaz de producir datos contradictorios. Es decir, las hipótesis científicas siempre son “riesgosas” debido a la afirmación de predecir los resultados de experimentos aún no realizados, y por lo tanto son susceptibles de desprevenirse si los experimentos no resultan como se predijo. Así, si una hipótesis predice con éxito los resultados de experimentos repetidos, se desprueba su falsedad.
La mecánica cuántica, primero como hipótesis y posteriormente como teoría, ha demostrado ser extremadamente exitosa en la predicción de resultados experimentales, de ahí el alto grado de confianza científica depositada en ella. Muchos científicos tienen razones para creer que se trata de una teoría incompleta, sin embargo, ya que sus predicciones se mantienen más en escalas micro físicas que en dimensiones macroescópicas, pero sin embargo es una teoría tremendamente útil para explicar y predecir las interacciones de partículas y átomos.
Como ya has visto en este capítulo, la física cuántica es esencial para describir y predecir muchos fenómenos diferentes. En la siguiente sección, veremos su significación en la conductividad eléctrica de sustancias sólidas, incluidos los semiconductores. En pocas palabras, nada en química o física de estado sólido tiene sentido dentro del marco teórico popular de electrones que existen como trozos discretos de materia, girando alrededor de núcleos atómicos como satélites en miniatura. Es cuando los electrones son vistos como “ondulaciones” existentes en estados definidos y discretos que se puede explicar el comportamiento regular y periódico de la materia.
Revisar
- Los electrones en los átomos existen en “nubes” de probabilidad distribuida, no como trozos discretos de materia orbitando el núcleo como pequeños satélites, como muestran las ilustraciones comunes de los átomos.
- Los electrones individuales alrededor de un núcleo atómico buscan “estados” únicos, descritos por cuatro números cuánticos: el Número Cuántico Principal, conocido como la concha; el Número Cuántico de Momentum Angular, conocido como la subcapa; el Cuántico Magnético Número, que describe el orbital (orientación de la subcapa); y el Número Cuántico de Espín, o simplemente giro. Estos estados se cuantifican, lo que significa que no existen condiciones “entre” para un electrón que no sean aquellos estados que encajan en el esquema de numeración cuántica.
- El Número Cuántico Principal (n) describe el nivel básico o caparazón en el que reside un electrón. Cuanto mayor sea este número, mayor radio tiene la nube de electrones del núcleo del átomo, y mayor es la energía de ese electrón. Los números cuánticos principales son números enteros (enteros positivos).
- El Número Cuántico de Momentum Angular (l) describe la forma de la nube de electrones dentro de una capa o nivel particular, y a menudo se conoce como la “subcapa”. Hay tantas subconchas (formas de nubes de electrones) en cualquier caparazón dado como el número cuántico principal de esa concha. Los números cuánticos de momento angular son enteros positivos que comienzan en cero y terminan en uno menos que el número cuántico principal (n-1).
- El Número Cuántico Magnético (m l) describe qué orientación tiene una subcapa (forma de nube de electrones). Los subshells pueden asumir tantas orientaciones diferentes como 2 veces el número de subshell (l) más 1, (2l+1) (por ejemplo, para l=1, ml= -1, 0, 1) y cada orientación única se llama orbital. Estos números son números enteros que van desde el valor negativo del número de subshell (l) hasta 0 hasta el valor positivo del número de subshell.
- El Número Cuántico de Espín (m s) describe otra propiedad de un electrón, y puede ser un valor de +1/2 o -1/2.
- El Principio de Exclusión de Pauli dice que no hay dos electrones en un átomo que puedan compartir exactamente el mismo conjunto de números cuánticos. Por lo tanto, no más de dos electrones pueden ocupar cada orbital (spin=1/2 y spin=-1/2), 2l+1 orbitales en cada subshell, y n subconchas en cada caparazón, y no más.
- La notación espectroscópica es una convención para denotar la configuración electrónica de un átomo. Las conchas se muestran como números enteros, seguidas de letras de subshell (s, p, d, f), con números en superíndice que suman el número de electrones que residen en cada subshell respectiva.
- El comportamiento químico de un átomo está determinado únicamente por los electrones en las conchas sin llenar. Las carcasas de bajo nivel que están completamente llenas tienen poco o ningún efecto sobre las características de unión química de los elementos.
- Los elementos con capas de electrones completamente llenas son casi completamente no reactivos, y se llaman nobles (antes conocidos como inertes).


