4.1: Circuitos de resistencia de CA (capacitivos)
- Page ID
- 153305
.png)
Circuito AC resistivo puro: el voltaje y la corriente están en fase.
Si tuviéramos que trazar la corriente y el voltaje para un circuito de CA muy simple que consiste en una fuente y una resistencia, (Figura arriba) se vería algo así: (Figura abajo)
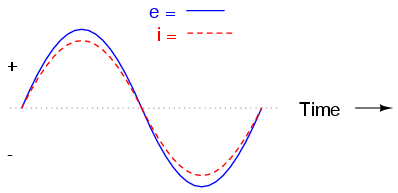.png)
Voltaje y corriente “en fase” para circuito resistivo.
Debido a que la resistencia permite una cantidad de corriente directamente proporcional al voltaje a través de ella en todos los períodos de tiempo, la forma de onda para la corriente está exactamente en fase con la forma de onda para el voltaje. Podemos mirar en cualquier momento a lo largo del eje horizontal de la gráfica y comparar esos valores de corriente y voltaje entre sí (cualquier mirada “instantánea” a los valores de una onda se conoce como valores instantáneos, es decir, los valores en ese instante en el tiempo). Cuando el valor instantáneo de voltaje es cero, la corriente instantánea a través de la resistencia también es cero. De igual manera, en el momento en que el voltaje a través de la resistencia está en su pico positivo, la corriente a través de la resistencia también está en su pico positivo, y así sucesivamente. En cualquier momento dado a lo largo de las ondas, la Ley de Ohm es válida para los valores instantáneos de voltaje y corriente.
También podemos calcular la potencia disipada por esta resistencia, y trazar esos valores en la misma gráfica: (Figura abajo)
.png)
La alimentación instantánea de CA en un circuito resistivo siempre es positiva.


