1.1: El conjunto de números reales

El conjunto de números reales consiste en los números que utilizamos en la vida cotidiana. Definiremos el conjunto de números reales con mayor precisión, pero primero, definamos algunos otros conjuntos de números.

Números Naturales: Los números de conteo que comienzan con 1:1, 2, 3, 4,...

Números Enteros: 0 y los números de conteo: 0, 1, 2, 3, 4,...

Enteros: Números enteros positivos y negativos (incluye 0); Los números enteros y sus opuestos:..., -4, -3, -2, -1, 0, 1, 2, 3, 4,...

Números racionales: Un número que se puede escribir como una fracción (enteros, decimales de terminación y decimales repetidos)

Números irracionales: Números que no se pueden escribir como fracción (decimales no terminales y decimales no repetitivos)

Números reales: Todos los números racionales e irracionales

Algunos números se pueden clasificar en muchas categorías. El siguiente diagrama muestra la relación entre los diferentes conjuntos de números.

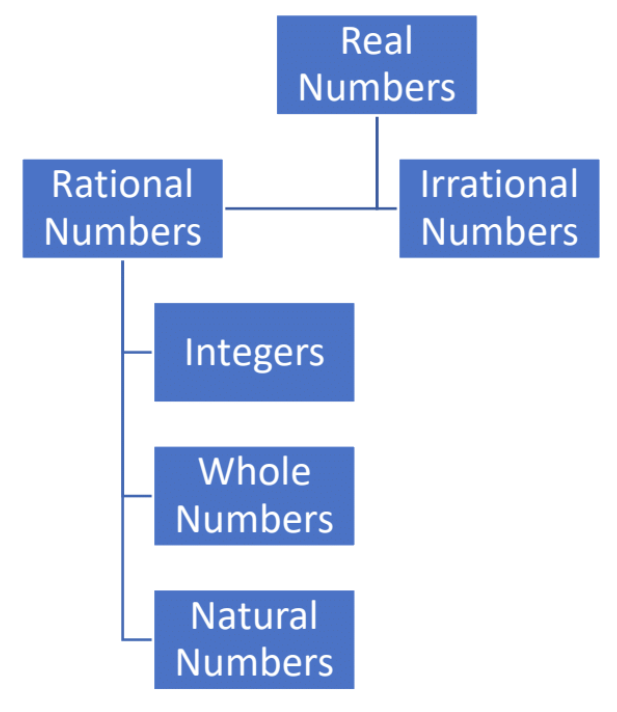
Ejemplo: Clasificar los siguientes números

1. 2.718
2. \(\sqrt{13}\)
3. \(\frac{24}{51} \)
4. 101
5. \(0.\overline{3}\)
6. -5

Vea el video para conocer las soluciones.

La línea del número real

Pedimos números reales en una recta numérica en función de su distancia desde 0. Los números positivos se encuentran a la derecha de cero y los números negativos se encuentran a la izquierda de cero. Cada punto en la recta numérica corresponde a un número real.

Observe que -2 está representado por una distancia de 2 unidades a la izquierda de cero, el negativo determina el lado de cero mientras que el 2 representa la distancia desde cero. De igual manera, +2 está representado por una distancia de 2 unidades a la derecha de cero, el positivo indica que nos movemos a la derecha de cero mientras que el 2 representa la distancia desde cero. Al escribir números positivos, es costumbre no escribir el signo “+” en el frente.

Ejemplo: Trazar los siguientes números en una recta numérica real

1. 2.718
2. \(\sqrt{13}\)
3. \(\frac{24}{51}\)
4. 101
5. \(0.\overline{3}\)
6. -5

Ver el video para una demostración.

Determinamos el tamaño de un número relativo a otro número usando signos menores que (\ <\) o mayores que (\(>\)). Cualquiera que sea el número que esté más a la derecha, es mayor, mientras que un número que está más a la izquierda es menor.

Decimos “\(a\)es menor que\(b\)” si\(a\) se encuentra a la izquierda de\(b\) en una recta numérica real y escribimos esto como:\(a < b\).

Decimos “\(a\)es mayor que\(b\)” si\(a\) se encuentra a la derecha de\(b\) en una recta numérica real y escribimos esto como:\(a >b\).

Ejemplos: Usar\(<\) o\(>\) para indicar la relación entre los números declarados

1. 7 ____ -3
2. 5 ____ 12
3. 5.8 ____ 5.7
4. -3.2 ____ -3.1
5. -5 ____ -12

Vea el video para conocer las soluciones.

Lo opuesto a un número y valor absoluto

Definición: Lo contrario de un número real,\(a\), es\(-a\).

Podemos pensar en lo contrario de un número real como cambiar el signo del número real.

Ejemplos: Lo contrario de 5 es -5. Lo opuesto de -7 es — (-7) = 7

De ahí que - (-7) se pueda leer como “lo opuesto de -7” o “lo opuesto de lo opuesto de 7” o 7.

Definición: El valor absoluto de un número real es su distancia de cero en una recta numérica real. La notación para el valor absoluto utiliza dos barras verticales a cada lado del número, de ahí que “el valor absoluto de a” se denotaría como\(\left|a\right|\). Dado que el valor absoluto representa una distancia, su valor siempre es positivo.

Ejemplos:

\(\left|5\right|\)= 5 ya que 5 es una distancia de 5 de 0

\(\left|-7\right|\)=7 ya que -7 es una distancia de 7 de 0