7.8: El Transistor Unijunction (UJT)
- Page ID
- 153664
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Transistor unijunction: Aunque un transistor unijunction no es un tiristor, este dispositivo puede activar tiristores más grandes con un pulso en la base B1. Un transistor unijunction está compuesto por una barra de silicio de tipo N que tiene una conexión de tipo P en el medio. Véase la figura a continuación (a). Las conexiones en los extremos de la barra se conocen como bases B1 y B2; el punto medio tipo P es el emisor. Con el emisor desconectado, la resistencia total R BBO, un elemento de hoja de datos, es la suma de R B1 y R B2 como se muestra en la Figura siguiente (b). R BBO varía de 4-12kΩ para diferentes tipos de dispositivos. La relación de separación intrínseca η es la relación de R B1 a R BBO. Varía de 0.4 a 0.8 para diferentes dispositivos. El símbolo esquemático es la Figura a continuación (c)
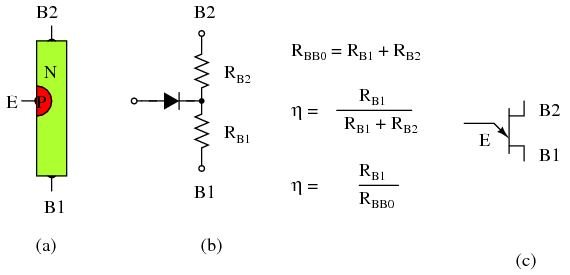
Transistor unijunction: (a) Construcción, (b) Modelo, (c) Símbolo
La curva característica de corriente de emisor uniunión vs voltaje (Figura abajo (a)) muestra que a medida que V E aumenta, la corriente I E aumenta hasta I P en el punto pico. Más allá del punto pico, la corriente aumenta a medida que disminuye el voltaje en la región de resistencia negativa. El voltaje alcanza un mínimo en el punto valle. La resistencia de R B1, la resistencia de saturación es más baja en el punto valle.
I P e I V, son parámetros de hoja de datos; Para un 2n2647, I P e I V son 2µA y 4mA, respectivamente. [AMS] V P es la caída de voltaje a través de R B1 más una caída de diodo de 0.7V; consulte la Figura a continuación (b). Se estima que V V es aproximadamente 10% de V BB.
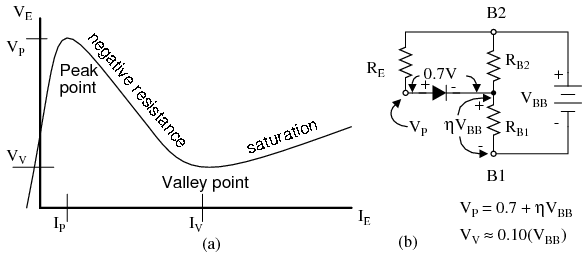
Transistor unijunction: (a) curva característica del emisor, (b) modelo para V P.
El oscilador de relajación en la Figura siguiente es una aplicación del oscilador uniunión. R E carga C E hasta el punto pico. El terminal emisor unijunction no tiene ningún efecto sobre el condensador hasta que se alcanza este punto. Una vez que el voltaje del condensador, V E, alcanza el punto de voltaje pico V P, la resistencia emisor-base1 E-B1 baja rápidamente descarga el condensador. Una vez que el condensador se descarga por debajo del punto valle V V, la resistencia E-RB1 vuelve a ser alta y el condensador es libre para cargarse nuevamente.
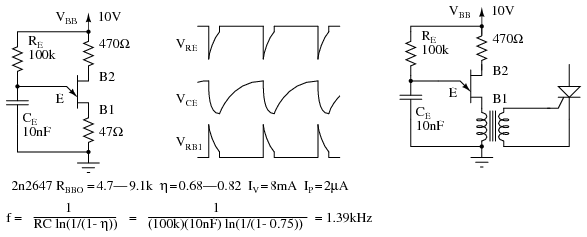
Oscilador de relajación de transistor uniunión y formas de onda. El oscilador acciona SCR.
Durante la descarga del condensador a través de la resistencia de saturación E-B1, se puede ver un pulso en las resistencias externas de carga B1 y B2, Figura anterior. La resistencia de carga en B1 necesita ser baja para no afectar el tiempo de descarga. La resistencia externa en B2 es opcional. Se puede sustituir por un cortocircuito. La frecuencia aproximada viene dada por 1/f = T = RC. Una expresión más precisa para la frecuencia se da en la Figura anterior.
La resistencia de carga R E debe estar dentro de ciertos límites. Debe ser lo suficientemente pequeño como para permitir que I P fluya basado en el suministro de V BB menos V P. Debe ser lo suficientemente grande como para suministrar I V basado en el suministro V BB menos V V. [MHW] Las ecuaciones y un ejemplo para un 2n2647:
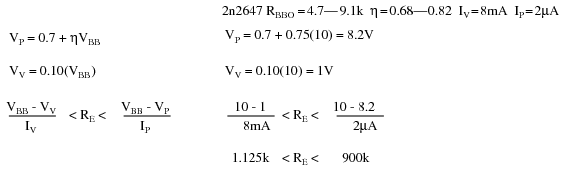
Transistor Unijunction Programable (PUT): Aunque el transistor unijunction está catalogado como obsoleto (leer caro si se puede obtener), el transistor unijunction programable está vivo y bien. Es económico y en producción. Aunque cumple una función similar al transistor unijunction, el PUT es un tiristor de tres terminales. El PUT comparte la estructura de cuatro capas típica de los tiristores que se muestra en la Figura siguiente. Tenga en cuenta que la puerta, una capa de tipo N cerca del ánodo, se conoce como una “puerta de ánodo”. Además, el cable de puerta en el símbolo esquemático está unido al extremo del ánodo del símbolo.
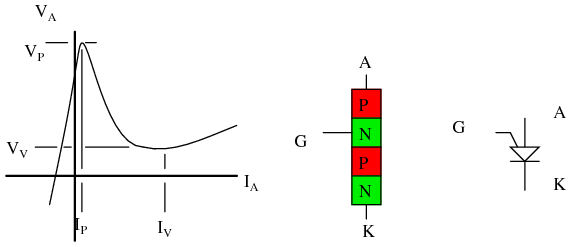
Transistor unijunction programable: Curva característica, construcción interna, símbolo esquemático.
La curva característica para el transistor unijunction programable en la Figura anterior es similar a la del transistor unijunction. Esta es una gráfica de la corriente del ánodo I A versus la tensión del ánodo V A. El voltaje del conductor de la puerta establece, programas, el voltaje pico del ánodo V P. A medida que aumenta la corriente del ánodo, el voltaje aumenta hasta el punto pico. A partir de entonces, el aumento de la corriente resulta en una disminución del voltaje, hasta el punto valle.
El equivalente PUT del transistor unijunction se muestra en la figura siguiente. Las resistencias PUT externas R1 y R2 reemplazan las resistencias internas del transistor unijunction R B1 y R B2, respectivamente. Estas resistencias permiten el cálculo de la relación intrínseca de separación η.
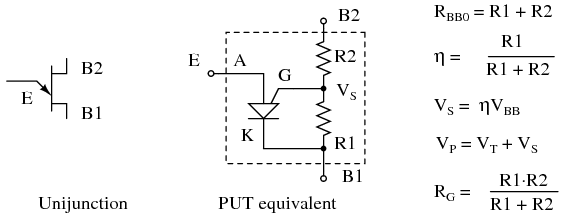
Equivalente a PUT del transistor unijunction
La siguiente figura muestra la versión PUT del oscilador de relajación uniunión Figura anterior. La resistencia R carga el condensador hasta el punto pico, Figura anterior, luego la conducción pesada mueve el punto de operación por la pendiente de resistencia negativa hasta el punto valle. Un pico de corriente fluye a través del cátodo durante la descarga del condensador, desarrollando un pico de voltaje a través de las resistencias del cátodo. Después de la descarga del condensador, el punto de operación se restablece de nuevo a la pendiente hasta el punto pico.
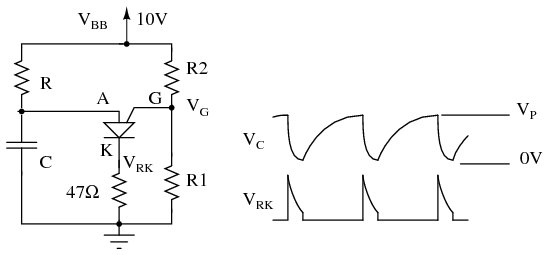
Oscilador de relajación PUT
Problema: ¿Cuál es el rango de valores adecuados para R en la Figura anterior, un oscilador de relajación? La resistencia de carga debe ser lo suficientemente pequeña como para suministrar suficiente corriente para elevar el ánodo a V P el punto pico (Figura anterior) mientras se carga el condensador. Una vez que se alcanza V P, el voltaje del ánodo disminuye a medida que aumenta la corriente (resistencia negativa), lo que mueve el punto de operación al valle. Es el trabajo del condensador suministrar la corriente valle I V. Una vez que se descarga, el punto de operación se restablece de nuevo a la pendiente ascendente hasta el punto pico. El resistor debe ser lo suficientemente grande como para que nunca suministre la corriente de valle alto I P. Si la resistencia de carga alguna vez pudiera suministrar tanta corriente, la resistencia suministraría la corriente valle después de que se descargara el condensador y el punto de operación nunca se reiniciaría a la condición de alta resistencia a la izquierda del punto pico.
Seleccionamos el mismo V BB =10V utilizado para el ejemplo de transistor unijunction. Seleccionamos valores de R1 y R2 para que η sea aproximadamente 2/3. Calculamos η y V S. El equivalente paralelo de R1, R2 es R G, que solo se utiliza para realizar selecciones de la Tabla siguiente. Junto con V S =10, el valor más cercano a nuestro 6.3, encontramos V T =0.6V, en la Tabla siguiente y calculamos V P.

También encontramos I P e I V, las corrientes pico y valle, respectivamente en la Tabla siguiente. Todavía necesitamos V V, el voltaje valle. Se utilizó 10% de V BB = 1V, en el ejemplo de uniunión anterior. Consultando la hoja de datos, encontramos el voltaje directo V F =0.8V a I F =50mA. La corriente del valle I V =70µA es mucho menor que I F =50mA. Por lo tanto, V V debe ser menor que V F =0.8V. ¿Cuánto menos? Para estar seguros configuramos V V =0V. Esto elevará un poco el límite inferior en el rango de resistencia.
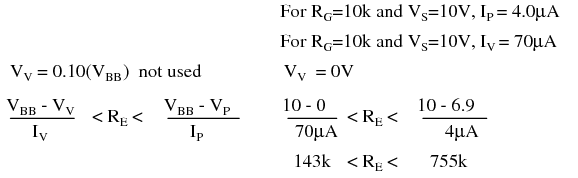
Elegir R > 143k garantiza que el punto de operación se pueda restablecer desde el punto valle después de la descarga del condensador. R < 755k permite cargar hasta V P en el punto pico.
La siguiente figura muestra el oscilador de relajación PUT con los valores finales de resistencia. También se muestra una aplicación práctica de un PUT que activa un SCR. Este circuito necesita un suministro sin filtrar V BB (no mostrado) dividido desde el rectificador puente para restablecer el oscilador de relajación después de cada cruce por cero de potencia. La resistencia variable debe tener una resistencia mínima en serie con ella para evitar que una configuración de olla baja cuelgue en el punto del valle.
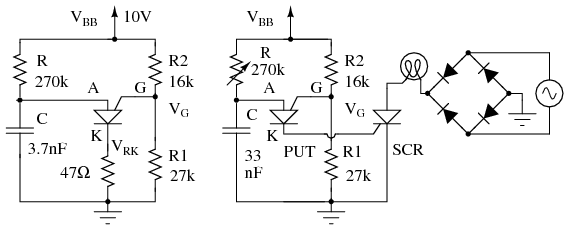
Oscilador de relajación PUT con valores de componentes. PUT impulsa el atenuador de lámpara SCR.
Se dice que los circuitos de temporización PUT son utilizables a 10 kHz. Si se requiere una rampa lineal en lugar de una rampa exponencial, reemplace la resistencia de carga con una fuente de corriente constante como un diodo de corriente constante basado en FET. Un PUT sustituto puede construirse a partir de un transistor de silicio PNP y NPN como se muestra para el circuito equivalente a SCS en la figura siguiente omitiendo la puerta del cátodo y usando la puerta del ánodo.
Revisar
- Un transistor unijunction consta de dos bases (B1, B2) unidas a una barra resistiva de silicio, y un emisor en el centro. La unión E-B1 tiene propiedades de resistencia negativa; puede cambiar entre resistencia alta y baja.
- Un PUT (transistor unijunction programable) es un tiristor de 4 capas de 3 terminales que actúa como un transistor unijunction. Una red de resistencias externas “programas” η.
- La relación de separación intrínseca es η=R1/ (R1+R2) para un PUT; sustituya R B1 y R B2, respectivamente, por un transistor unijunction. El voltaje de disparo está determinado por η.
- Los transistores unijunction y los transistores unijunction programables se aplican a osciladores, circuitos de temporización y activación de tiristores.


