11.2: Contadores asíncronos
- Page ID
- 154406
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En la sección anterior, vimos un circuito usando un flip-flop J-K que contaba hacia atrás en una secuencia binaria de dos bits, de 11 a 10 a 01 a 00. Dado que sería deseable tener un circuito que pudiera contar hacia adelante y no solo hacia atrás, valdría la pena examinar nuevamente una secuencia de conteo hacia adelante y buscar más patrones que pudieran indicar cómo construir dicho circuito.
Como sabemos que las secuencias de conteo binario siguen un patrón de división de frecuencia de octava (factor de 2), y que los multivibradores flip-flop J-K establecidos para el modo “toggle” son capaces de realizar este tipo de división de frecuencia, podemos imaginar un circuito compuesto por varios flip-flops J-K, en cascada para producir cuatro bits de salida. El principal problema que enfrentamos es determinar cómo conectar estos flip-flops juntos para que se alternen en los momentos adecuados para producir la secuencia binaria adecuada. Examine la siguiente secuencia de conteo binario, prestando atención a los patrones que preceden al “alternar” de un bit entre 0 y 1:
.png)
Tenga en cuenta que cada bit en esta secuencia de cuatro bits se alterna cuando el bit anterior a él (el bit que tiene una importancia menor, o peso de posición), alterna en una dirección particular: de 1 a 0. Las flechas pequeñas indican aquellos puntos en la secuencia donde un bit cambia, la cabeza de la flecha apuntando al bit anterior haciendo la transición de un estado “alto” (1) a un estado “bajo” (0):

Comenzando con cuatro flip-flops J-K conectados de tal manera que siempre estén en el modo “toggle”, necesitamos determinar cómo conectar las entradas de reloj de tal manera que cada bit siguiente se conmute cuando el bit anterior pasa de 1 a 0. Las salidas Q de cada flip-flop servirán como los bits binarios respectivos del recuento final de cuatro bits:
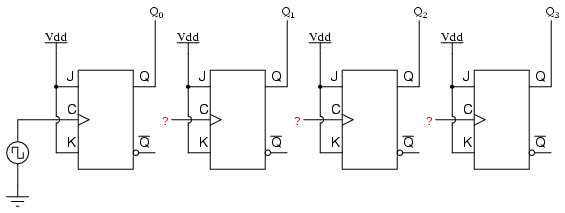
Si usáramos flip-flops con activación de borde negativo (símbolos de burbuja en las entradas del reloj), simplemente podríamos conectar la entrada de reloj de cada flip-flop a la salida Q del flip-flop anterior a él, de modo que cuando el bit anterior cambie de un 1 a un 0, el “borde descendente” de esa señal “cronometraría” el siguiente flip-flop para alternar el siguiente bit:
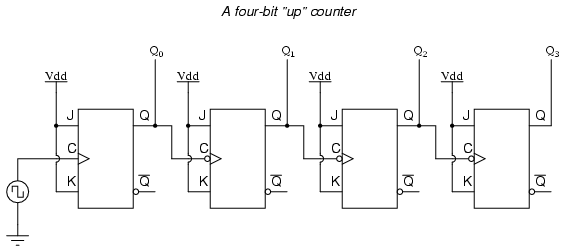
Este circuito produciría las siguientes formas de onda de salida, cuando “sincronizadas” por una fuente repetitiva de pulsos de un oscilador:
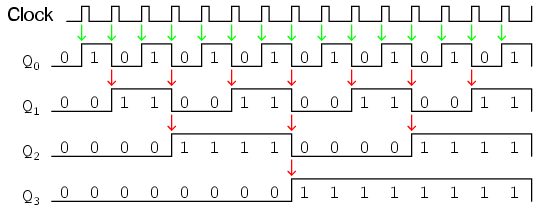
El primer flip-flop (el que tiene la salida Q 0), tiene una entrada de reloj activada por borde positivo, por lo que alterna con cada borde ascendente de la señal de reloj. Observe cómo la señal de reloj en este ejemplo tiene un ciclo de trabajo inferior al 50%. He mostrado la señal de esta manera con el propósito de demostrar cómo la señal de reloj no necesita ser simétrica para obtener bits de salida confiables y “limpios” en nuestra secuencia binaria de cuatro bits. En el primer circuito flip-flop mostrado en este capítulo, utilicé la propia señal de reloj como uno de los bits de salida. Sin embargo, esta es una mala práctica en el diseño de contadores, porque requiere el uso de una señal de onda cuadrada con un ciclo de trabajo del 50% (tiempo “alto” = tiempo “bajo”) para obtener una secuencia de conteo donde todos y cada uno de los pasos se detienen por la misma cantidad de tiempo. El uso de un flip-flop J-K para cada bit de salida, sin embargo, nos alivia de la necesidad de tener una señal de reloj simétrica, permitiendo el uso de prácticamente cualquier variedad de formas de onda alta/baja para incrementar la secuencia de conteo.
Como indican todas las demás flechas en el diagrama de pulsos, cada bit de salida siguiente es alternado por la acción del bit anterior que pasa de “alto” (1) a “bajo” (0). Este es el patrón necesario para generar una secuencia de conteo “up”.
Una solución menos obvia para generar una secuencia “arriba” usando flip-flops activados por borde positivo es “registrar” cada flip-flop usando la salida Q' del flip-flop anterior en lugar de la salida Q. Dado que la salida Q' siempre será exactamente el estado opuesto de la salida Q en un flip-flop J-K (sin estados inválidos con este tipo de flip-flop), una transición de alto a bajo en la salida Q irá acompañada de una transición de bajo a alto en la salida Q'. En otras palabras, cada vez que la salida Q de un flip-flop pasa de 1 a 0, la salida Q' del mismo flip-flop pasará de 0 a 1, proporcionando el pulso de reloj positivo necesitaríamos alternar un flip-flop activado por borde positivo en el momento adecuado:
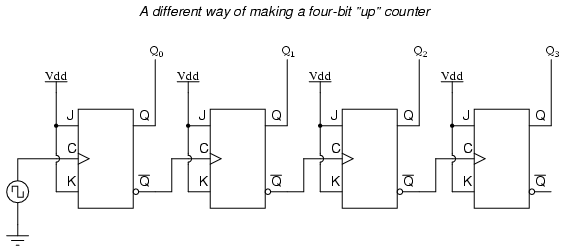
Una forma en que podríamos ampliar las capacidades de cualquiera de estos dos circuitos contadores es considerar las salidas Q' como otro conjunto de cuatro bits binarios. Si examinamos el diagrama de pulsos para dicho circuito, vemos que las salidas Q' generan una secuencia de conteo descendente, mientras que las salidas Q generan una secuencia de conteo hacia arriba:
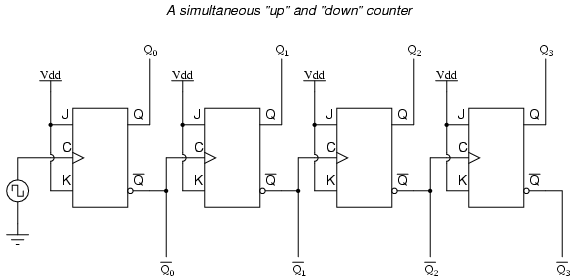
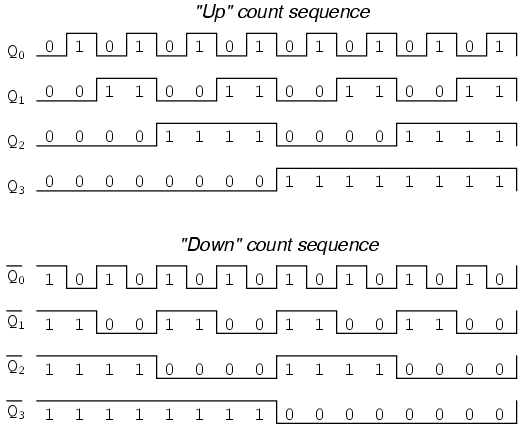
Desafortunadamente, todos los circuitos de contador mostrados hasta ahora comparten un problema común: el efecto dominó. Este efecto se ve en ciertos tipos de sumador binario y circuitos de conversión de datos, y se debe a retardos de propagación acumulativos entre puertas en cascada. Cuando la salida Q de un flip-flop pasa de 1 a 0, ordena al siguiente flip-flop alternar. Si el siguiente toggle flip-flop es una transición de 1 a 0, ordenará al flip-flop después de él que se active también, y así sucesivamente. Sin embargo, dado que siempre hay una pequeña cantidad de retardo de propagación entre el comando para alternar (el pulso de reloj) y la respuesta de alternancia real (Q y Q' genera estados cambiantes), cualquier flip-flops posterior que se conmutará algún tiempo después de que el primer flip-flop haya alternado. Por lo tanto, cuando múltiples bits se alternan en una secuencia de conteo binario, no todos alternarán exactamente al mismo tiempo:
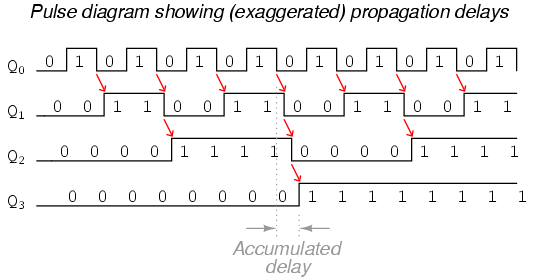
Como puede ver, cuantos más bits se alternen con un pulso de reloj dado, más severo es el tiempo de retardo acumulado de LSB a MSB. Cuando se produce un pulso de reloj en dicho punto de transición (por ejemplo, en la transición de 0111 a 1000), los bits de salida se “ondularán” en secuencia de LSB a MSB, ya que cada bit siguiente cambia y ordena al siguiente bit alternar también, con una pequeña cantidad de retardo de propagación entre cada alternancia de bit. Si echamos un vistazo de cerca a este efecto durante la transición de 0111 a 1000, podemos ver que habrá falsos recuentos de salida generados en el breve periodo de tiempo en el que tenga lugar el efecto “ripple”:
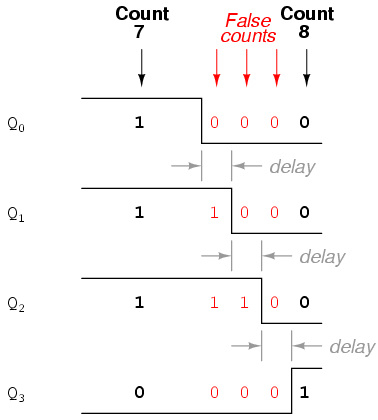
En lugar de pasar limpiamente de una salida “0111” a una salida “1000”, el circuito contador ondulará muy rápidamente de 0111 a 0110 a 0100 a 0000 a 1000, o de 7 a 6 a 4 a 0 y luego a 8. Este comportamiento le da al circuito contador el nombre de contador de ondulación, o contador asíncrono.
En muchas aplicaciones, este efecto es tolerable, ya que la ondulación ocurre muy, muy rápidamente (el ancho de los retrasos se ha exagerado aquí como una ayuda para entender los efectos). Si todo lo que quisiéramos hacer era accionar un conjunto de diodos emisores de luz (LEDs) con las salidas del contador, por ejemplo, esta breve ondulación no tendría ninguna consecuencia en absoluto. Sin embargo, si quisiéramos usar este contador para accionar las entradas “selectas” de un multiplexor, indexar un puntero de memoria en un circuito de microprocesador (computadora) o realizar alguna otra tarea donde salidas falsas pudieran causar errores espurios, no sería aceptable. Existe una manera de utilizar este tipo de circuito contador en aplicaciones sensibles a salidas falsas generadas por ondas, e implica un principio conocido como estroboscópico.
La mayoría de los circuitos descodificadores y multiplexores están equipados con al menos una entrada llamada “habilitar”. Las salidas de dicho circuito estarán activas solo cuando se active la entrada de habilitación. Podemos usar esta entrada de habilitación para estrobosar el circuito que recibe la salida del contador de ondulación para que se desactive (y por lo tanto no responda a la salida del contador) durante el breve período de tiempo en el que las salidas del contador podrían estar ondulando, y habilitado solo cuando haya pasado suficiente tiempo desde el último pulso de reloj que toda ondulación habrá cesado. En la mayoría de los casos, la señal estroboscópica puede ser el mismo pulso de reloj que acciona el circuito contador:
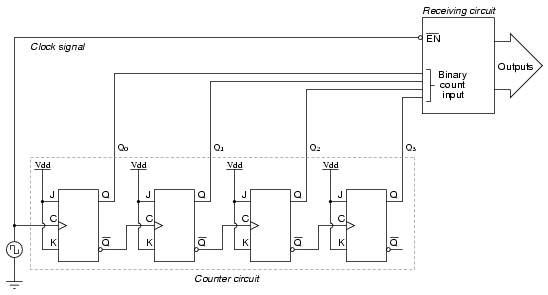
Con una entrada Active-low Enable, el circuito receptor responderá a la cuenta binaria del circuito contador de cuatro bits solo cuando la señal de reloj es “baja”. Tan pronto como el pulso de reloj pasa “alto”, el circuito receptor deja de responder a la salida del circuito contador. Dado que el circuito contador es activado por borde positivo (según lo determinado por la primera entrada de reloj biestable), toda la acción de conteo tiene lugar en la transición de baja a alta de la señal de reloj, lo que significa que el circuito receptor se desactivará justo antes de que ocurra cualquier alternancia en el contador los cuatro bits de salida del circuito. El circuito receptor no se habilitará hasta que la señal de reloj vuelva a un estado bajo, que debería ser un tiempo lo suficientemente largo después de que toda ondulación haya dejado de ser “segura” para permitir que la nueva cuenta tenga efecto en el circuito receptor. El parámetro crucial aquí es el tiempo “alto” de la señal de reloj: debe ser al menos tan largo como el período de ondulación máximo esperado del circuito contador. De lo contrario, la señal de reloj habilitará prematuramente el circuito receptor, mientras aún se está produciendo alguna ondulación.
Otra desventaja del circuito contador asíncrono, o ondulación, es la velocidad limitada. Si bien todos los circuitos de puerta están limitados en términos de frecuencia de señal máxima, el diseño de circuitos contadores asíncronos agrava este problema al hacer que los retardos de propagación sean aditivos. Por lo tanto, incluso si se usa la luz estroboscópica en el circuito receptor, un circuito contador asíncrono no se puede cronometrar a ninguna frecuencia mayor que la que permite que el mayor retardo de propagación acumulado posible transcurra mucho antes del siguiente pulso.
La solución a este problema es un circuito contador que evita la ondulación por completo. Dicho circuito contador eliminaría la necesidad de diseñar una característica de “estroboscópico” en cualquier circuito digital que use la salida del contador como entrada, y también disfrutaría de una velocidad de operación mucho mayor que su equivalente asíncrono. Este diseño de circuito contador es el tema de la siguiente sección.
Revisar
- Se puede hacer un contador “arriba” conectando las entradas de reloj de los flip-flops J-K activados por borde positivo a las salidas Q' de los flip-flops anteriores. Otra forma es usar flip-flops activados de borde negativo, conectando las entradas de reloj a las salidas Q de los flip-flops anteriores. En cualquier caso, las entradas J y K de todos los flip-flops están conectadas a V cc o V dd para estar siempre “altas”.
- Los circuitos de contador hechos a partir de biestables J-K en cascada donde cada entrada de reloj recibe sus pulsos de la salida del flip-flop anterior exhiben invariablemente un efecto dominó, donde se generan falsos recuentos de salida entre algunos pasos de la secuencia de conteo. Estos tipos de circuitos de contador se denominan contadores asíncronos o contadores de ondulación.
- El estroboscópico es una técnica aplicada a los circuitos que reciben la salida de un contador asíncrono (ondulación), de manera que los recuentos falsos generados durante el tiempo de ondulación no tendrán ningún efecto negativo. Esencialmente, la entrada de habilitación de dicho circuito está conectada al pulso de reloj del contador de tal manera que se habilita solo cuando las salidas del contador no están cambiando, y se desactivará durante aquellos períodos de cambio de salidas del contador donde se produce la ondulación.


