13.2.1: Convertidor digital a analógico de entrada ponderada binaria DAC R/2nr
( \newcommand{\kernel}{\mathrm{null}\,}\)
¿Qué es un circuito DAC R/2nr?
El circuito R/2nr DAC, también conocido como DAC de entrada ponderada binaria, es una variación en el circuito de amplificador operacional de suma de inversión. (Tenga en cuenta que los circuitos de “suma” a veces también se conocen como circuitos “de verano”). Si recuerda, el circuito sumador inversor clásico es un amplificador operacional que utiliza retroalimentación negativa para ganancia controlada, con varias entradas de voltaje y una salida de voltaje. El voltaje de salida es la suma invertida (polaridad opuesta) de todos los voltajes de entrada:
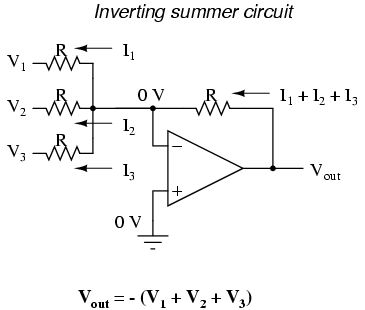
Para un circuito sumador de inversión simple, todas las resistencias deben ser de igual valor. Si alguna de las resistencias de entrada fuera diferente, los voltajes de entrada tendrían diferentes grados de efecto en la salida, y el voltaje de salida no sería una suma verdadera.
Ejemplo: Un DAC R/2nr con múltiples valores de resistencia de entrada
Consideremos, sin embargo, establecer intencionalmente las resistencias de entrada en diferentes valores. Supongamos que deberíamos establecer los valores de resistencia de entrada en múltiples potencias de dos: R, 2R y 4R, en lugar de todos el mismo valor R:
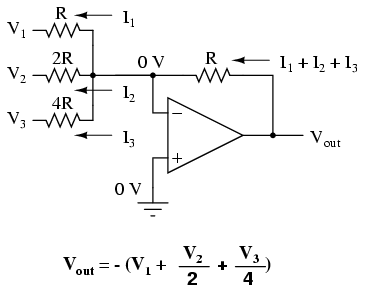
A partir de V 1 y pasando por V 3, esto daría a cada voltaje de entrada exactamente la mitad del efecto en la salida como el voltaje anterior a él. En otras palabras, el voltaje de entrada V 1 tiene un efecto 1:1 sobre el voltaje de salida (ganancia de 1), mientras que el voltaje de entrada V 2 tiene la mitad de ese efecto en la salida (una ganancia de 1/2), y V 3 la mitad de eso (una ganancia de 1/4). Estas proporciones no fueron elegidas arbitrariamente: son las mismas proporciones correspondientes para colocar pesos en el sistema de numeración binaria.
Si accionamos las entradas de este circuito con puertas digitales para que cada entrada sea de 0 voltios o voltaje de alimentación completo, el voltaje de salida será una representación analógica del valor binario de estos tres bits.
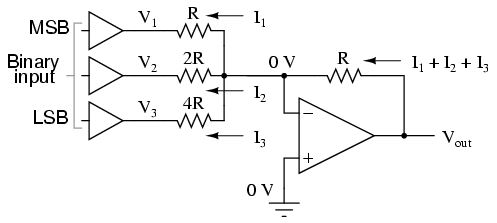
Si graficamos los voltajes de salida para las ocho combinaciones de bits binarios (000 a 111) ingresados a este circuito, obtendremos la siguiente progresión de voltajes:
Tenga en cuenta que con cada paso en la secuencia de conteo binario, se produce un cambio de 1.25 voltios en la salida.
Este circuito es muy fácil de simular usando SPICE. En la siguiente simulación, configuré el circuito DAC con una entrada binaria de 110 (anote los primeros números de nodo para las resistencias R1, R2 y R 3: un número de nodo de “1” lo conecta al lado positivo de una batería de 5 voltios, y un número de nodo de “0” lo conecta a tierra).
El voltaje de salida aparece en el nodo 6 en la simulación:
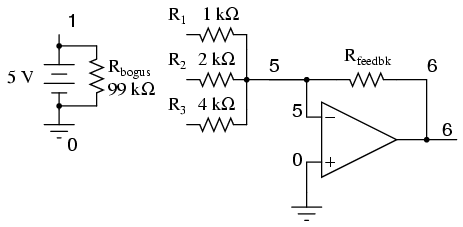
Podemos ajustar los valores de las resistencias en este circuito para obtener voltajes de salida directamente correspondientes a la entrada binaria. Por ejemplo, al hacer la resistencia de retroalimentación 800 Ω en lugar de 1 kΩ, el DAC emitirá -1 voltio para la entrada binaria 001, -4 voltios para la entrada binaria 100, -7 voltios para la entrada binaria 111, y así sucesivamente.
Si queremos expandir la resolución de este DAC (agregar más bits a la entrada), todo lo que necesitamos hacer es agregar más resistencias de entrada, manteniendo la misma secuencia de valores de potencia de dos:
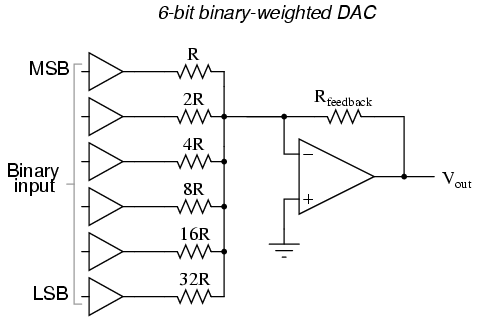
Cabe señalar que todas las puertas lógicas deben emitir exactamente los mismos voltajes cuando están en el estado “alto”.
Si una puerta está emitiendo +5.02 voltios para un “alto” mientras que otra está emitiendo solo +4.86 voltios, la salida analógica del DAC se verá afectada negativamente. Asimismo, todos los niveles de voltaje “bajo” deben ser idénticos entre compuertas, idealmente 0.00 voltios exactamente. Se recomienda que se utilicen puertas de salida CMOS, y que se elijan valores de resistencia de entrada/salida para minimizar la cantidad de corriente que cada puerta tiene para fuente o sumidero.



