6.2: Tasas de Filtración
- Page ID
- 152587
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Uno de los procesos más importantes en una planta de tratamiento de agua es la filtración. Es la última barrera entre el proceso de tratamiento y el cliente. Los filtros atrapan o eliminan partículas del agua reduciendo aún más la turbidez o turbidez. Hay diferentes formas, tamaños y tipos de filtros que contienen un lecho o una combinación de lechos de arena, carbón antracita o alguna otra forma de material granular.
Los filtros de arena lentos son el tipo más antiguo de filtración de agua municipal y tienen tasas de filtración que varían de 0.015 a 0.15 galones por minuto por pie cuadrado de área de lecho filtrante, dependiendo de la gradación del medio filtrante y la calidad del agua cruda. Los filtros de arena rápidos, por otro lado, pueden tener tasas de filtración que van desde 2.0 a 10 galones por minuto por pie cuadrado de área de lecho filtrante. Por lo general, los filtros de arena rápidos requerirán ciclos de retrolavado más frecuentes para eliminar los desechos atrapados de los filtros.
El lavado a contracorriente es la inversión del flujo a través de los filtros a una velocidad mayor para eliminar las partículas obstruidas de los filtros. Los tiempos de ejecución del lavado a contracorriente pueden ser de 5 a 20 minutos con tasas que van desde 8 a 25 galones por minuto por pie cuadrado de área de lecho filtrante, dependiendo de la calidad del agua prefiltrada.
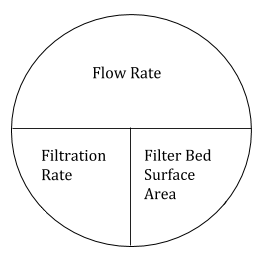
Las tasas de filtración y retrolavado se calculan dividiendo el caudal a través del filtro por el área superficial del lecho filtrante. Por lo general, estas tasas se miden en galones por minuto por pie cuadrado de área del lecho filtrante.
- Caudal (gpm) /Superficie (pies cuadrados) = Velocidad de filtración
Aunque las tasas de filtración se expresan comúnmente como gpm/ft 2, también se expresan como la distancia de caída (en pulgadas) dentro del filtro por unidad de tiempo (en minutos). Durante el lavado a contracorriente se expresa con las mismas unidades solo por “subida” en el filtro. Vea el ejemplo a continuación.
- Tasa de Filtración = Caída (pulgadas) /Tiempo (min)
- Tasa de retrolavado = Aumento (pulgadas) /Tiempo (min)
Ejemplos
Express 2.5 gpm/ft 2 como in/min.
Primero, convierta gpm a cfm. El propósito de esto es comenzar a hacer coincidir la unidad de “pulgadas” en in/min con los “pies cúbicos en cfm.
- (2.5 gal/min) /sq.ft x 1 cf/7.48 gal = 0.33 cfm/sq.ft
- 2.5 gpm/sq.ft x 1 cf/7.48 gal = 0.33 cfm/sq.ft
Si miras la respuesta anterior de (0.33 cf/m) /sq.ft más de cerca puedes ver que también se puede expresar como 0.33 pies/min ya que los pies cuadrados y cf se cancelan entre sí a pies.
Una vez que tengas “pies por minuto” puedes convertir fácilmente a “pulgadas por minuto” multiplicando por 12.
- 0.33 pies/min x 12 pulgadas/1 ft = 4 pulgadas/min
Probemos otro ejemplo: ¿Cuál es la tasa de filtración a través de un filtro de 20' por 20' si el flujo promedio a través del tratamiento es 2.5 MG?
Primero, convierta 2.5 MGD a gpm. Para ello divide 2.5 MGD por 1,440.
- 2,500,000 gal/día x 1 día/1,440 min = 1,736 gpm
Luego divida el flujo por el área del filtro (20' x 20' = 400 pies cuadrados).
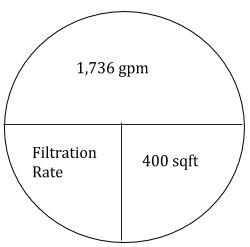
- 1,736 gpm/400 pies cuadrados = 4.34 gpm/pies cuadrados
Ahora, calcula las pulgadas por minuto.
En lugar de 7.48 galones por pie cúbico y 12 pulgadas por pie, existe un factor de conversión que también se puede utilizar.
- 1.6 pulgadas/min = 1 gpm/sq.ft
Ejercicios
-
Una planta de tratamiento de agua procesa 10.5 MGD. ¿Cuál es el área requerida del lecho filtrante necesaria para mantener una tasa de filtración de 1.75 gpm/ft 2?
-
Un filtro de 15 pies por 17 pies necesita ser lavado a fondo a una velocidad de 17 gpm/ft 2 por un mínimo de 20 minutos. ¿Cuántos galones se utilizan durante el proceso de retrolavado?
-
Con el fin de lavar correctamente un cierto filtro se necesita una tasa de retrolavado de 20 pulgadas por minuto de aumento. Si el filtro mide 20 pies por 25 pies, ¿cuál es el caudal de retrolavado en gpm?
-
Una planta de tratamiento de agua procesa un máximo de 18.65 MGD. La planta tiene 6 filtros que miden 20 pies por 22 pies cada uno. Suponiendo que cada filtro recibe una cantidad igual de flujo ¿cuál es la tasa de filtración en gpm/ft 2?
-
Una planta de tratamiento de agua procesa 4.55 MGD a través de un filtro de 35 pies por 35 pies. ¿Cuáles son las pulgadas por minuto correspondientes a través del filtro?
-
Un filtro se lava a contracorriente a una velocidad de 15.5 pulgadas por minuto durante 25 minutos. Si el filtro es de 150 pies 2, ¿cuántos galones se usaron?
-
Un ingeniero está diseñando un filtro circular para manejar 5.75 MGD y mantener una velocidad de filtración de 1.75 pulgadas por minuto. ¿Cuál será el diámetro?
-
Un filtro necesita ser lavado a contracorriente cuando la tasa de caída excede 3.1 pulgadas por minuto. Se determinó que esta tasa se alcanza después de 2.3 MG a través de un filtro de 17 pies por 17 pies. ¿Con qué frecuencia necesita retrolavado el filtro? Da tu respuesta en la unidad de tiempo más lógica.


