6: Algunos datos geométricos sobre triángulos y paralelogramos

Círculos

Para un círculo con radio\(r\):

• Circunferencia:\(C = 2\pi r\)
• Área:\(A = \pi r^{2}\)

Triángulos

• La suma de las medidas de los tres ángulos de un triángulo es\(180^\circ\).
• Un triángulo en el que cada ángulo tiene una medida menor que\(90^\circ\) se denomina triángulo agudo.
• Un triángulo que tiene un ángulo cuya medida es mayor que\(90^\circ\) se llama triángulo obtuso.
• Un triángulo que contiene un ángulo cuya medida\(90^\circ\) se llama triángulo rectángulo. El lado de un triángulo rectángulo que está opuesto al ángulo recto se llama hipotenusa, y los otros dos lados se llaman las piernas.
• Un triángulo isósceles es un triángulo en el que dos lados del triángulo tienen la misma longitud. En este caso, los dos ángulos a través de los dos lados de igual longitud tienen igual medida.
• Un triángulo equilátero es un triángulo en el que los tres lados tienen la misma longitud. Cada ángulo de un triángulo equilátero tiene una medida de\(60^\circ\).

Triángulos rectos

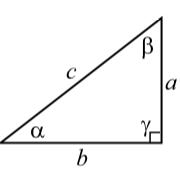
• La suma de las medidas de los dos ángulos agudos de un triángulo rectángulo es\(90^\circ\). En el diagrama de la derecha,\(\alpha + \beta = 90^\circ\).
• El Teorema de Pitágoras. En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros dos lados. En el diagrama de la derecha,\(c^{2} = a^{2} + b^{2}\)

Triángulos Retos Especiales

Un triángulo rectángulo en el que se encuentran ambos ángulos agudos\(\textbf{45}^\circ\). Para este tipo de triángulo rectángulo, las longitudes de las dos patas son iguales. Entonces si\(c\) es la longitud de la hipotenusa y\(x\) es la longitud de cada una de las piernas, entonces por el Teorema de Pitágoras,\(c^{2} = x^{2} + x^{2}\). Resolviendo esta ecuación para\(x\), obtenemos

\[2x^{2} = c^{2}\]
\[x^{2} = \dfrac{c^{2}}{2}\]
\[x = \sqrt{\dfrac{c^{2}}{2}}\]
\[x = \dfrac{x}{\sqrt{2}} = \dfrac{c\sqrt{2}}{2}\]

Un triángulo rectángulo con ángulos agudos de\(\textbf{30}^\circ\) y\(\textbf{60}^\circ\).

Comenzamos con un triángulo equilátero con lados de longitud\(c\). Al dibujar una bisectriz angular en uno de los vértices, creamos dos triángulos rectos congruentes con ángulos agudos de\(30^\circ\) y\(60^\circ\).

Esto significa que el tercer lado de cada uno de estos triángulos rectos tendrá una longitud de\(\dfrac{c}{2}\). Si la longitud de la altitud es\(x\), entonces usando el Teorema de Pitágoras, obtenemos

\[c^{2} = x^{2} + (\dfrac{c}{2})^{2}\]
\[x^{2} = c^{2} - \dfrac{c^{2}}{4}\]
\[x^{2} = \dfrac{3c^{2}}{4}\]
\[x = \sqrt{\dfrac{3c^{2}}{4}} = \dfrac{c\sqrt{3}}{2}\]

Triángulos similares

Dos triángulos son similares si los tres ángulos de un triángulo son iguales en medida a los tres ángulos del otro triángulo. El siguiente diagrama muestra triángulos similares\(\triangle{ABC}\) y\(\triangle{DEF}\). Escribimos\(\triangle{ABC} \sim \triangle{DEF}\).

Los lados de triángulos similares no tienen que tener la misma longitud pero serán proporcionales. Usando la notación en el diagrama, esto significa que

\[\dfrac{a}{d} = \dfrac{b}{e} = \dfrac{c}{f}\]

Paralelogramos

Utilizamos algunas propiedades de los paralelogramos en el estudio de vectores en la Sección 3.5. Un paralelogramo es un cuadrilátero con dos pares de lados paralelos. Usaremos el diagrama de la derecha para describir algunas propiedades de los paralelogramos.

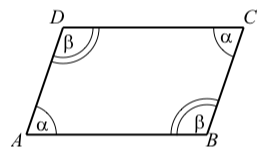
• Los lados opuestos son iguales en longitud. En el diagrama, esto significa que\[AB = DC \space \text{and} \space AD = BC\]
• Como se muestra en el diagrama, los ángulos opuestos son iguales. Es decir,\[\angle{DAB} = \angle{BCD} \space \text{and} \space \angle{ABC} = \angle{CDA}\]
• La suma de dos ángulos adyacentes es\(180^\circ\). En el diagrama, esto significa que\[\alpha + \beta = 180^\circ\]