5.E: Números Complejos y Coordenadas Polares (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 113375

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ejercicio$\PageIndex{1}$

Escribe cada uno de los siguientes como un número complejo en forma estándar.

\[(4 + i) + (3 - 3i)\]
\[5(2 - i) + i(3 - 2i)\]
\[(4 + 2i)(5 - 3i)\]
\[(2 + 3i)(1 + i) + (4 - 3i)\]

Responder

$(4 + i) + (3 - 3i) = 7 - 2i$
$5(2 - i) + i(3 -2i) = 12 - 2i$
$(4 + 2i)(5 - 3i) = 26 - 2i$
$(2 + 3i)(1 + i) + (4 - 3i) = 3 + 2i$

Ejercicio$\PageIndex{2}$

Utilice la fórmula cuadrática para escribir las dos soluciones de cada una de las siguientes ecuaciones cuadráticas en forma estándar.

\[x^{2} - 3x + 5 = 0\]
\[2x^{2} = x - 7\]

Responder: a)$x = \dfrac{3}{2} + \dfrac{\sqrt{11}}{2}i, x = \dfrac{3}{2} - \dfrac{\sqrt{11}}{2}i$.

Ejercicio$\PageIndex{3}$

Para cada uno de los siguientes pares de números complejos$w$ y$z$, determinar la suma$w + z$ e ilustrar la suma con un diagrama.

\[w = 3 + 2i, z = 5 - 4i.\]
\[w = 4i, z = -3 + 2i.\]
\[w = 5, z = -7 + 2i.\]
\[w = 6 - 3i, z = -1 + 7i.\]

Responder

$w + z = 8 - 2i$
$w + z = -3 + 6i$

Ejercicio$\PageIndex{4}$

Para cada uno de los siguientes números complejos$z$, determine$\bar{z}$,$|z|$, y$z\bar{z}$.

\[z = 5 + 2i\]
\[z = 3i\]
\[z = 3 - 4i\]
\[z = 7 + i\]

Responder

$\bar{z} = 5 + 2i, |z| = \sqrt{29}, z\bar{z} = 29$
$\bar{z} = -3i, |z| = 3, z\bar{z} = 9$

Ejercicio$\PageIndex{5}$

Escribe cada uno de los siguientes cocientes en forma estándar.

\[\dfrac{5 + i}{3 + 2i}\]
\[\dfrac{3 + 3i}{i}\]
\[\dfrac{i}{2 - i}\]
\[\dfrac{4 + 2i}{1 - i}\]

Responder

$\dfrac{5 + i}{3 + 2i} = \dfrac{17}{13} - \dfrac{7}{13}i$
$\dfrac{3 + 3i}{i} = 3 - 3i$

Ejercicio$\PageIndex{6}$

Eso lo sabemos$i^{1} = i$ y$i^{2} = -1$. Entonces podemos ver que\[i^{3} = i^{2}\cdot i = (-1)i = -i.\]
$i^{4} = 1$Demuéstralo.
Ahora determinar$i^{5}, i^{6}, i^{7}$, y$i^{8}$. Nota: Cada poder de$i$ voluntad igual$1, -1, i$, o$-i$.
Fíjese en eso$12 = 4\cdot 3 + 1$. Utilizaremos esto para determinar$i^{13}$. \[i^{13} = i^{4\cdot 3 + 1} = i^{4\cdot 3}i^{1} = (i^{4})^{3}\cdot i\]Entonces, ¿qué es$i^{13}$?
Usando$39 = 4\cdot 9 + 3$, determinar$i^{39}$.
Determinar$i^{54}$.

Ejercicio$\PageIndex{7}$

Escriba el número complejo$i(2 + 2i)$ en forma estándar. Trazar los números complejos$2 + 2i$ y$i(2 + 2i)$ en el plano complejo. ¿Cuál parece ser el ángulo entre estos dos números complejos?
Repita la parte (a) para los números complejos$2 - 3i$ y$i(2 - 3i)$.
Repita la parte (a) para los números complejos$3i$ y$i(3i)$.
Describa lo que sucede cuando el número complejo$a + bi$ se multiplica por el número complejo$i$.


Para dar sentido a soluciones de ecuaciones cuadráticas que no son reales, introducimos números complejos. Aunque los números complejos surgen naturalmente al resolver ecuaciones cuadráticas, su introducción en las matemáticas surgió del problema de resolver ecuaciones cúbicas.

Ejercicio$\PageIndex{8}$

Determinar la forma polar (trigonométrica) de cada uno de los siguientes números complejos.

\[3 +3i\]
\[3 -3i\]
\[-3 +3i\]
\[5i\]
\[4\sqrt{3} + 4i\]
\[-4\sqrt{3} - 4i\]

Responder

$3 + 3i = \sqrt{18}(\cos(\dfrac{\pi}{4}) + i\sin(\dfrac{\pi}{4}))$
$4\sqrt{3} + 4i = 8(\cos(\dfrac{\pi}{6}) + i\sin(\dfrac{\pi}{6}))$

Ejercicio$\PageIndex{9}$

En cada una de las siguientes$z$ se da un número complejo. En cada caso, determinar los números reales$a$ y$b$ así eso$z = a + bi$. Si no es posible determinar valores exactos para$a$ y$b$, determinar los valores de$a$ y$b$ corregir a cuatro decimales.

\[z = 5(\cos(\dfrac{\pi}{2}) + i\sin(\dfrac{\pi}{2}))\]
\[z = 2.5(\cos(\dfrac{\pi}{4}) + i\sin(\dfrac{\pi}{4}))\]
\[z = 2.5(\cos(\dfrac{3\pi}{4}) + i\sin(\dfrac{3\pi}{4}))\]
\[z = 3(\cos(\dfrac{7\pi}{6}) + i\sin(\dfrac{7\pi}{6}))\]
\[z = 8(\cos(\dfrac{7\pi}{10}) + i\sin(\dfrac{7\pi}{10}))\]

Responder

$5\cos(\dfrac{\pi}{2}) + i\sin(\dfrac{\pi}{2}) = 5i$
$2.5(\cos(\dfrac{\pi}{4}) + i\sin(\dfrac{\pi}{4})) = 1.25\sqrt{2} + 1.25\sqrt{2}i$

Ejercicio$\PageIndex{10}$

Para cada una de las siguientes, escriba el producto$wz$ en polar (forma trigonométrica). Cuando sea posible, escribe el producto en forma$a + bi$, donde$a$ y$b$ son números reales y no implican una función trigonométrica.

\[w = 5(\cos(\dfrac{\pi}{12}) + i\sin(\dfrac{\pi}{12})), z = 2(\cos(\dfrac{5\pi}{12}) + i\sin(\dfrac{5\pi}{12}))\]
\[w = 2.3(\cos(\dfrac{\pi}{3}) + i\sin(\dfrac{\pi}{3})), z = 2(\cos(\dfrac{5\pi}{4}) + i\sin(\dfrac{5\pi}{4}))\]
\[w = 2(\cos(\dfrac{7\pi}{10}) + i\sin(\dfrac{7\pi}{10})), z = 2(\cos(\dfrac{2\pi}{5}) + i\sin(\dfrac{2\pi}{5}))\]
\[w = (\cos(24^\circ) + i\sin(24^\circ)), z = 2(\cos(33^\circ) + i\sin(33^\circ))\]
\[w = 2(\cos(72^\circ) + i\sin(72^\circ)), z = 2(\cos(78^\circ) + i\sin(78^\circ))\]

Responder

$wz = 10(\cos(\dfrac{6\pi}{12}) + i\sin(\dfrac{6\pi}{12})) = 10i$
$wz = 6.9(\cos(\dfrac{19\pi}{12}) + i\sin(\dfrac{19\pi}{12}))$

Ejercicio$\PageIndex{11}$

Para los números complejos en Ejercicio$\PageIndex{10}$, escriba el cociente$\dfrac{w}{z}$ en polar (forma trigonométrica). Cuando sea posible, escribe el cociente en forma$a + bi$, donde$a$ y$b$ son números reales y no implican una función trigonométrica.Agrega texto aquí. Para que el número automático funcione, es necesario agregar la plantilla “AutoNum” (preferiblemente al final) a la página.

Responder

a)$\dfrac{w}{z} = \dfrac{5}{2}(\cos(\dfrac{-4\pi}{12}) + i\sin(\dfrac{-4\pi}{12})) = \dfrac{5}{4} - \dfrac{5\sqrt{3}}{4}i$

b)$\dfrac{w}{z} = \dfrac{23}{30}(\cos(\dfrac{-11\pi}{12}) + i\sin(\dfrac{-11\pi}{12}))$

Ejercicio$\PageIndex{12}$

Escribe el número complejo$i$ en forma polar.
Vamos$z = r(\cos(\theta) + i\sin(\theta))$. Determinar el producto$i\cdot z$ en forma polar. Usa esto para explicar por qué el número complejo$i\cdot z$ y$z$ será perpendicular cuando ambos sean trazados en el plano complejo.

: La multiplicación de números complejos es más complicada que la suma de números complejos. Para comprender mejor el producto de números complejos, primero investigamos la forma trigonométrica (o polar) de un número complejo. Esta forma trigonométrica conecta el álgebra con la trigonometría y será útil para encontrar rápida y fácilmente poderes y raíces de números complejos.

Ejercicio$\PageIndex{13}$

Utilice el Teorema de Demoivre para determinar cada una de las siguientes potencias de un número complejo. Escribe la respuesta en la forma$a + bi$, donde$a$ y$b$ son números reales y no implican el uso de una función trigonométrica.

\[(2 + 2i)^{6}\]
\[(\sqrt{3} + i)^{8}\]
\[(\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i)^{3}\]
\[2(\cos(\dfrac{\pi}{15}) + i\sin(\dfrac{\pi}{15}))^{10}\]
\[(1 + i\sqrt{3})^{-4}\]
\[(-3 + 3i)^{-3}\]

Responder

a)$(2 + 2i)^{6} = [\sqrt{8}(\cos(\dfrac{\pi}{4}) + i\sin(\dfrac{\pi}{4}))]^{6} = 512i$

b)$(\sqrt{3} + i)^{8} = [2(\cos(\dfrac{\pi}{6}) + i\sin(\dfrac{\pi}{6}))]^{8} = -128 - 128\sqrt{3}i$

Ejercicio$\PageIndex{14}$

En cada una de las siguientes, determinar las raíces indicadas del número complejo dado. Cuando sea posible, escribir las raíces en la forma a C bi, donde a andb son números reales y no implican el uso de una función trigonométrica. De lo contrario, dejar las raíces en forma polar.

Las dos raíces cuadradas de$16i$.
Las dos raíces cuadradas de$2 + 2i\sqrt{3}$.
Las tres raíces cubitas de$5(\cos(\dfrac{3\pi}{4}) + i\sin(\dfrac{3\pi}{4}))$.
Las cinco quintas raíces de la unidad.
Las cuatro cuartas raíces de$(\dfrac{1}{2} - \dfrac{\sqrt{3}}{2}i)$.
Las tres raíces cubitas de$1 + \sqrt{3}i$.

Responder

(a) Escribir$16i = 16(\cos(\dfrac{\pi}{2}) + i\sin(\dfrac{\pi}{2}))$. Las dos raíces cuadradas de$16i$ son\[4(\cos(\dfrac{\pi}{4}) + i\sin(\dfrac{\pi}{4})) = 2\sqrt{2} + 2i\sqrt{2}\]

\[4(\cos(\dfrac{5\pi}{4}) + i\sin(\dfrac{5\pi}{4})) = -2\sqrt{2} - 2i\sqrt{2}\]

c) Las tres raíces cubitas de$5(\cos(\dfrac{3\pi}{4}) + i\sin(\dfrac{3\pi}{4}))$ son

\[\sqrt[3]{5}(\cos(\dfrac{\pi}{4}) + i\sin(\dfrac{\pi}{4})) = \sqrt[3]{5}(\dfrac{\sqrt{2}}{2} + \dfrac{\sqrt{2}}{2}i)\]
\[\sqrt[3]{5}(\cos(\dfrac{11\pi}{12}) + i\sin(\dfrac{11\pi}{12}))\]
\[\sqrt[3]{5}(\cos(\dfrac{19\pi}{12}) + i\sin(\dfrac{19\pi}{12}))\]

: La forma trigonométrica de un número complejo proporciona una manera relativamente rápida y fácil de calcular productos de números complejos. Como consecuencia, podremos calcular rápidamente potencias de números complejos, e incluso raíces de números complejos.

Ejercicio$\PageIndex{15}$

Trazar los siguientes puntos con las coordenadas polares especificadas.

$e1.png$

Figura$\PageIndex{1}$

\[(7, \dfrac{\pi}{6})\]\[(3, \dfrac{3\pi}{4})\]\[(2, \dfrac{-\pi}{3})\]

\[(3, \dfrac{7\pi}{4})\]\[(5, \dfrac{-\pi}{4})\]\[(4, \dfrac{11\pi}{4})\]

\[(6, \dfrac{11\pi}{6})\]\[(-3, \dfrac{2\pi}{3})\]\[(-5, \dfrac{5\pi}{6})\]

Responder

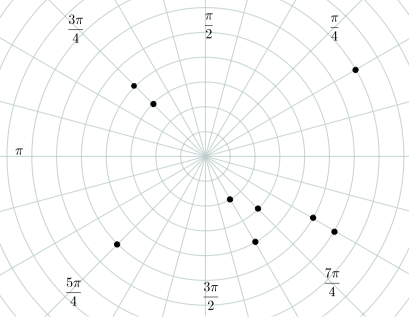
$5.4.png$

Figura$\PageIndex{2}$

Ejercicio$\PageIndex{16}$

Para cada uno de los siguientes puntos en coordenadas polares, determine tres representaciones diferentes en coordenadas polares para el punto. Utilice un valor positivo para la distancia radial$r$ para dos de las representaciones y un valor negativo para la distancia radial$r$ para la otra representación.

\[(5, 30^\circ)\]
\[(4, 100^\circ)\]
\[(-2, 50^\circ)\]
\[(7, -60^\circ)\]

Contestar

a) Algunas respuestas correctas son:$(5, 390^\circ)$,$(5, -330^\circ)$, y$(-5, 210^\circ)$.

b) Algunas respuestas correctas son:$(4, 460^\circ)$,$(4, -260^\circ)$, y$(-4, 280^\circ)$.

Ejercicio$\PageIndex{17}$

\[(5, \dfrac{\pi}{6})\]
\[(4, \dfrac{5\pi}{9})\]
\[(-2, \dfrac{5\pi}{18})\]
\[(7, -\dfrac{\pi}{3})\]

Contestar

Algunas respuestas correctas son:$(5, \dfrac{13\pi}{6})$,$(5, -\dfrac{11\pi}{6})$, y$(-5, \dfrac{7\pi}{6})$.
Algunas respuestas correctas son:$(4, \dfrac{23\pi}{9})$,$(4, -\dfrac{13\pi}{9})$, y$(-4, \dfrac{14\pi}{9})$.

Ejercicio$\PageIndex{18}$

Determine las coordenadas rectangulares para cada uno de los siguientes puntos en coordenadas polares:

\[(10, \dfrac{2\pi}{3})\]
\[(8, \dfrac{7\pi}{6})\]
\[(-5, \dfrac{5\pi}{4})\]
\[(10, -\dfrac{2\pi}{3})\]
\[(3, \dfrac{5\pi}{3})\]
\[(6, -\dfrac{\pi}{6})\]

Contestar

1. $(-5, 5\sqrt{3})$

3. $(\dfrac{5\sqrt{2}}{2}, \dfrac{5\sqrt{2}}{2})$

Ejercicio$\PageIndex{19}$

Determinar las coordenadas polares para cada uno de los siguientes puntos en coordenadas rectangulares. Utilice una distancia radial positiva$r$ y un ángulo polar con$0 \leq \theta < 2\pi$. Cuando sea necesario, utilice una función trigonométrica inversa y redondee el ángulo (en radianes) a la milésima más cercana.

\[(\dfrac{-5\sqrt{3}}{2}, \dfrac{5}{2})\]
\[(3, 5)\]
\[(\sqrt{2}, -\sqrt{2})\]
\[(-3, -4)\]

Contestar

1. $(5, \dfrac{5\pi}{6})$

2. $(\sqrt{34}, \tan^{-1}(\dfrac{5}{3})) \approx (\sqrt{34}, 1.030)$

Ejercicio$\PageIndex{20}$

Convierte cada una de las siguientes ecuaciones polares en una ecuación rectangular. Si es posible, escriba la ecuación rectangular con$y$ como una función de$x$.

\[r = 5\]
\[\theta = \dfrac{\pi}{3}\]
\[r = 8\cos(\theta)\]
\[r = 1 - \sin(\theta)\]
\[r^{2}\sin(2\theta) = 1\]
\[r = 1 - 2\cos(\theta)\]
\[r = \dfrac{3}{\sin(\theta) + 4\cos(\theta)}\]

Contestar

1. $x^{2} + y^{2} = 25$

2. $y = \dfrac{\sqrt{3}}{3}x$

4. $x^{2} + y^{2} = \sqrt{x^{2} + y^{2}} - y$

Ejercicio$\PageIndex{21}$

Convierte cada una de las siguientes ecuaciones rectangulares en una ecuación polar. Si es posible, escriba la ecuación polar con$r$ como una función de$\theta$.

\[x^{2} + y^{2} = 36\]
\[y = 4\]
\[x = 7\]
\[x^{2} - 6x + y^{2} = 0\]
\[x + y = 4\]
\[y = x^{2}\]

Contestar

2. $r\sin(\theta) = 4$o$r = \dfrac{4}{\sin(\theta)}$

5. $r\cos(\theta) + r\sin(\theta) = 4$o$r = \dfrac{4}{\cos(\theta) + \sin(\theta)}$

Ejercicio$\PageIndex{8}$

Que un sea un número real positivo.

Convierte la ecuación polar$r = 2a\sin(\theta)$ a rectangular y luego explica por qué la gráfica de esta ecuación es un círculo. ¿Cuál es el radio del círculo y cuál es el centro del círculo en coordenadas rectangulares?

Convierte la ecuación polar$r = 2a\cos(\theta)$ a rectangular y luego explica por qué la gráfica de esta ecuación es un círculo. ¿Cuál es el radio del círculo y cuál es el centro del círculo en coordenadas rectangulares?

: En nuestro estudio de la trigonometría hasta el momento, siempre que graficamos una ecuación o ubicamos un punto en el plano, hemos utilizado coordenadas rectangulares (o cartesianas). El uso de este tipo de sistema de coordenadas revolucionó las matemáticas ya que proporcionó el primer vínculo sistemático entre geometría y álgebra. Aunque el sistema de coordenadas rectangulares es muy importante, existen otros métodos para ubicar puntos en el plano. Estudiaremos uno de esos sistemas en esta sección.