5.3: Ensamblaje Genómico II- Métodos de gráfico de cuerdas
- Page ID
- 54139
La secuenciación de escopeta, que es un método de secuenciación más moderno y económico, da lecturas de alrededor de 100 bases de longitud. La longitud más corta de las lecturas da como resultado muchas más repeticiones de longitud mayor que la de las lecturas. Por lo tanto, necesitamos algoritmos nuevos y más sofisticados para hacer el ensamblaje del genoma correctamente.
Definición y construcción del gráfico de cuerdas
La idea detrás del ensamblaje del gráfico de cuerdas es similar a la gráfica de lecturas que vimos en la sección 5.2.2. En definitiva, estamos construyendo una gráfica en la que los nodos son datos de secuencia y los bordes se superponen, para luego tratar de encontrar la ruta más robusta a través de todos los bordes para representar nuestra secuencia subyacente.
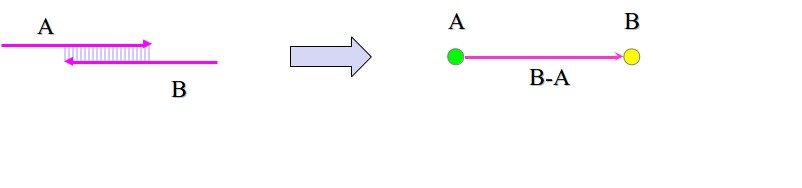
Figura 5.10: Construcción de un gráfico de cadenas.
A partir de las lecturas que obtenemos de la secuenciación de Shotgun, se construye un gráfico de cadenas agregando un borde para cada par de lecturas superpuestas. Tenga en cuenta que los vértices de la gráfica denotan cruces, y los bordes corresponden a la cadena de bases. Un solo nodo corresponde a cada lectura, y llegar a ese nodo mientras recorre la gráfica equivale a leer todas las bases hasta el final de la lectura correspondiente al nodo. Por ejemplo, en la figura 5.10, tenemos dos lecturas superpuestas A y B y son las únicas lecturas que tenemos. El gráfico de cadena correspondiente tiene dos nodos y dos aristas. Un borde no tiene un vértice en su extremo de cola, y tiene A en su extremo de cabeza. Este borde denota todas las bases en la lectura A. El segundo borde va del nodo A al nodo B, y solo denota las bases en B-A (la parte de lectura B que no se solapa con A). De esta manera, cuando atravesamos los bordes una vez, leemos toda la región exactamente una vez. En particular, observe que no atravesamos el solapamiento de la lectura A y la lectura B dos veces.
© fuente desconocida. Todos los derechos reservados. Este contenido está excluido de nuestra licencia Creative Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use/.
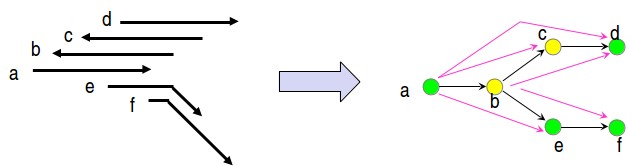
Figura 5.11: Construyendo un gráfico de cadenas 99
Hay un par de sutilezas en el gráfico de cuerdas (figura 5.11) que deben mencionarse:
- Tenemos dos colores diferentes para los nodos ya que el ADN se puede leer en dos direcciones. Si la superposición es entre las lecturas tal cual, entonces los nodos reciben los mismos colores. Y si el solapamiento es entre una lectura y las bases complementarias de la otra lectura, entonces reciben diferentes colores.
- En segundo lugar, si A y B se superponen, entonces hay ambigüedad en si dibujamos un borde de A a B, o de B a A. Tal ambularidad necesita resolverse de manera consistente en los cruces causados por repeticiones.
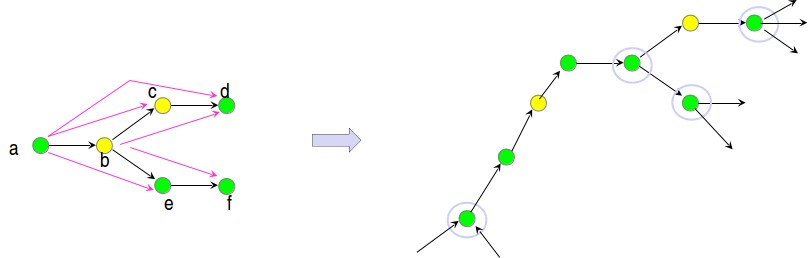
Figura 5.12: Ejemplo de gráfico de cuerdas sometido a remoción de bordes transitivos.
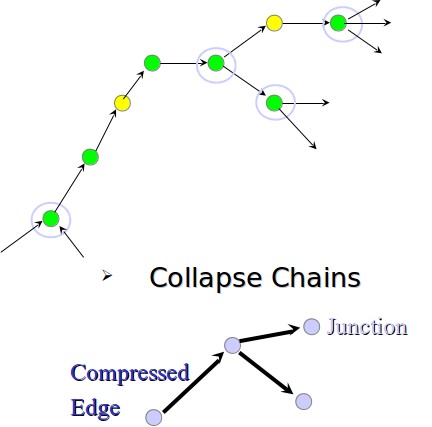
Figura 5.13: Ejemplo de gráfico de cadenas en proceso de colapso de cadena.
Después de construir el gráfico de cadenas a partir de lecturas superpuestas, nosotros: -
• Eliminar bordes transitivos: Los bordes transitivos son causados por superposiciones transitivas, es decir, una superposición B se superpone a C de tal manera que A se superpone a C. Hay algoritmos aleatorios que eliminan bordes transitivos en O (E) tiempo de ejecución esperado. En la figura 5.12, se puede ver el ejemplo de eliminación de bordes transitivos.
• Contraer cadenas: Después de eliminar los bordes transitivos, el gráfico que construimos tendrá muchas cadenas donde cada nodo tiene un borde entrante y un borde saliente. Derrumbamos todas estas cadenas a un solo borde. Un ejemplo de ello se muestra en la figura 5.13.
Flujos y consistencia gráfica
Después de hacer todo lo mencionado anteriormente obtendremos una gráfica bastante compleja, es decir, seguirá teniendo una serie de uniones debido a repeticiones relativamente largas en el genoma en comparación con la longitud de las lecturas. Ahora veremos cómo se pueden utilizar los conceptos de flujos para hacer frente a las repeticiones.
Primero, estimamos el peso de cada borde por el número de lecturas que obtenemos corresponde al borde. Si tenemos el doble del número de lecturas para algún borde que el número de ADN que secuenciamos, entonces es justo suponer que esta región del genoma se repite. Sin embargo, esta técnica por sí misma no es lo suficientemente precisa. De ahí que a veces podamos hacer estimaciones diciendo que el peso de algún borde es ≥ 2, y no asignarle un número particular.
Figura 5.14: Izquierda: Concepto de resolución de flujo. Derecha: Ejemplo de resolución de flujo
Utilizamos el razonamiento a partir de flujos para resolver tales ambigüedades. Necesitamos satisfacer la restricción de flujo en cada cruce, es decir, el peso total de todos los bordes entrantes debe ser igual al peso total de todos los bordes salientes. Por ejemplo, en la figura 5.14 hay una unión con un borde entrante de peso 1, y dos bordes salientes de peso ≥ 0 y ≥ 1. De ahí que podamos inferir que los pesos de los bordes salientes son exactamente iguales a 0 y 1 respectivamente. De esta manera se pueden inferir muchos pesos aplicando iterativamente este mismo proceso a lo largo de toda la gráfica.
Flujo factible
Una vez que tenemos la gráfica y los pesos de borde, ejecutamos un algoritmo de flujo de costos mínimos en la gráfica. Dado que los genomas más grandes pueden no tener un flujo de costo mínimo único, iterativamente hacemos lo siguiente:
• Agregar penalización ε a todos los bordes en solución
• Resolver flujo nuevamente - si hay un flujo de costo mínimo alternativo, ahora tendrá un costo menor en relación con el flujo anterior
• Repita hasta que no encontremos nuevos bordes
Después de hacer lo anterior, podremos etiquetar cada borde como uno de los siguientes
• Requerido: bordes que formaban parte de todas las soluciones
• No confiables: bordes que formaban parte de algunas de las soluciones
• No requeridos: bordes que no formaban parte de ninguna solución
Cómo lidiar con errores de secuenciación
Existen diversas fuentes de errores en el procedimiento de secuenciación del genoma. Los errores son generalmente de dos tipos diferentes, locales y globales.
Los errores locales incluyen inserciones, deleciones y mutaciones. Dichos errores locales se tratan cuando buscamos lecturas superpuestas. Es decir, mientras verificamos si las lecturas se superponen, verificamos si hay superposiciones mientras somos tolerantes hacia los errores de secuenciación. Una vez que hemos calculado las superposiciones, podemos derivar un consenso mediante mecanismos como la eliminación de indels y mutaciones que no son apoyadas por ninguna otra lectura y son contradicidas por al menos 2.
Los errores globales son causados por otros mechasismos como dos secuencias diferentes que se combinan antes de ser leídas, y de ahí obtenemos una lectura que es de diferentes lugares del genoma. Tales lecturas se llaman chimers. Estos errores se resuelven mientras se busca un flujo factible en la red. Cuando el borde correspondiente a la quimera está en uso, la cantidad de flujo que atraviesa este borde es menor en comparación con la capacidad de flujo. De ahí que el borde pueda ser detectado y luego ignorado.
Cada paso del algoritmo se hace lo más robusto y resistente posible a los errores de secuenciación. Y el número de ADN divididos y secuenciados se decide de una manera para que seamos capaces de construir la mayor parte del ADN (es decir, cumplir con alguna garantía de calidad como 98% o 95%).
Recursos
Algunos ensambladores de genoma populares que utilizan gráficos de cadena se enumeran a continuación
- Euler (Pevzner, 2001/06): Indización → Debruijn grafos → picking paths → consenso
- Valvel (Birney, 2010): Lecturas cortas → genomas pequeños → simplificación → corrección de errores
- ALLPATH (Gnerre, 2011): Lecturas cortas → genomas grandes → saltar datos → incertidumbre


