5.4: Alineación del Genoma Completo
- Page ID
- 54117
Una vez que tenemos acceso a secuencias del genoma completo para varias especies diferentes, podemos intentar alinearlas para inferir el camino que tomó la evolución para diferenciar estas especies. En esta sección discutimos algunos de los métodos para realizar alineaciones de genoma completo entre múltiples especies.
Alineación global, local y 'glocal'
El algoritmo de Needleman-Wunsch discutido en el capítulo 2 es la mejor manera de generar un alineamiento óptimo entre dos o más secuencias genómicas de tamaño limitado. A nivel de genomas completos, sin embargo, el límite de tiempo O (n 2) no es práctico. Además, para encontrar un alineamiento óptimo entre k especies diferentes, el tiempo para el algoritmo de Needleman-Wunsch se extiende a O (n k). Para genomas que tienen millones de bases de largo, este tiempo de ejecución es prohibitivo (Figura 5.15).
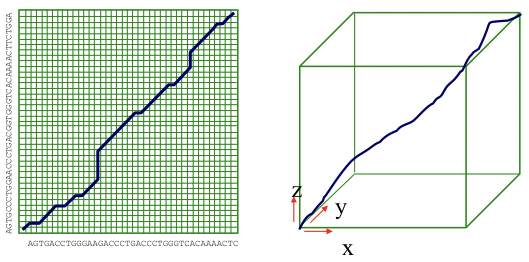
Figura 5.15: El algoritmo de Needleman-Wunsch para alineaciones de 2 y 3 genomas
Una alternativa es usar una herramienta de alineación local eficiente como BLAST para encontrar todas las alineaciones locales y luego encadenarlas a lo largo de la diagonal para formar alineaciones globales. Este enfoque puede ahorrar una cantidad significativa de tiempo, ya que el proceso de búsqueda de alineaciones locales es muy eficiente, y entonces solo necesitamos realizar el algoritmo de Needleman-Wunsch que consume mucho tiempo en los pequeños rectángulos entre alineaciones locales (Figura 5.16).
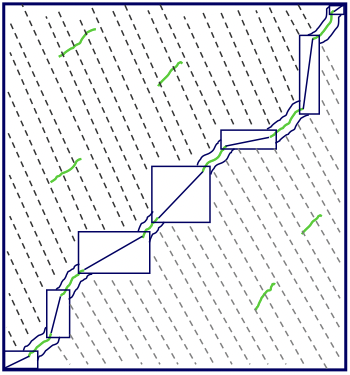
Figura 5.16: Podemos ahorrar tiempo al realizar una alineación global al encontrar primero todas las alineaciones locales y luego encadenarlas a lo largo de la diagonal con programación dinámica restringida.
Otro enfoque novedoso para el alineamiento del genoma completo es extender la búsqueda de alineamiento local para incluir inversiones, duplicaciones y translocaciones. Entonces podemos encadenar estos elementos usando las transformaciones de menor costo entre secuencias. Este enfoque se denomina comúnmente alineación glocal, ya que busca combinar lo mejor de la alineación local y global para crear la imagen más precisa de cómo evolucionan los genomas a lo largo del tiempo (Figura 5.17).
Lagan: Encadenamiento de alineaciones locales
LAGAN es un popular kit de herramientas de software que incorpora muchas de las ideas anteriores y se puede utilizar para alineaciones locales, globales, glocales y múltiples entre especies.
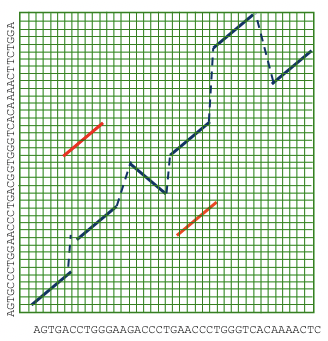
Figura 5.17: La alineación glocal permite la posibilidad de duplicaciones, inversiones y translocaciones.
El algoritmo LAGAN regular consiste en encontrar alineaciones locales, encadenar alineaciones locales a lo largo de la diagonal y luego realizar programación dinámica restringida para encontrar la ruta óptima entre alineaciones locales.
Multi-lagan utiliza el mismo enfoque que el LAGAN regular pero lo generaliza a la alineación de múltiples especies. En este algoritmo, el usuario debe proporcionar un conjunto de genomas y un árbol filogenético correspondiente. Multi- LAGAN realiza alineamiento por pares guiado por el árbol filogenético. Primero compara especies altamente relacionadas, y luego compara iterativamente especies cada vez más distantes.
Shuffle-lagan es una herramienta de alineación glocal que encuentra alineaciones locales, construye un mapa de homología aproximado y luego alinea globalmente cada una de las partes consistentes (Figura 5.18). Para construir un mapa de homología, el algoritmo elige el subconjunto de puntuación máxima de alineaciones locales en función de ciertas penalizaciones de brecha y transformación, que forman una cadena no decreciente en al menos una de las dos secuencias. A diferencia del LAGAN regular, todas las secuencias de alineación local posibles se consideran como pasos en el alineamiento glocal, ya que podrían representar translocaciones, inversiones y translocaciones invertidas, así como secuencias regulares no transformadas. Una vez que se ha construido el mapa de homología aproximado, el algoritmo divide las regiones homólogas en trozos de alineaciones locales que están aproximadamente a lo largo de la misma ruta continua. Finalmente, se aplica el algoritmo LAGAN a cada fragmento para vincular las alineaciones locales mediante programación dinámica restringida.
Al ejecutar Shuffle-lagan u otras herramientas de alineación glocal, podemos descubrir inversiones, translocaciones y otras relaciones homólogas entre diferentes especies. Al mapear las conexiones entre estos rangos traseros, podemos obtener una idea de cómo evolucionó cada especie a partir del ancestro común (Figura 5.19).


