10.5: Problema de plegamiento de ARN y enfoques

Por último, llegamos al punto en el que queremos estudiar la estructura del ARN. El objetivo aquí es predecir la estructura secundaria del ARN, dada su estructura primaria (o su secuencia). La buena noticia es que podemos encontrar la estructura óptima usando programación dinámica. Ahora para configurar nuestro marco de programación dinámica necesitaríamos un esquema de puntuación, el cual crearíamos utilizando la contribución de cada emparejamiento de bases a la estabilidad física de la molécula. Es decir, queremos crear una estructura con mínima energía libre, en nuestro modelo simple asignaríamos a cada par base un valor energético. 10.7

Figura 10.7: Ejemplo de un esquema de puntuación para partidos de pares base. Tenga en cuenta que G-U puede formar un par de bamboleo en ARN.

La estructura óptima va a ser la que tenga un mínimo de energía libre y por convención la energía negativa se estabiliza, y la energía positiva no se estabiliza. Usando este marco, podemos usar programación dinámica (DP) para calcular la estructura óptima porque 1) este esquema de puntuación es aditivo 2) no permitimos pseudo nudos, lo que significa que podemos dividir el ARN en dos más pequeños que son independientes, y resolver el problema de estos ARN más pequeños.

Queremos encontrar una matriz DP E _ij, en la que calculemos la energía libre mínima para la subsecuencia i a j. El primer acercamiento a esto es el algoritmo de Nussinov.

Algoritmo de Nussinov

La fórmula de recursión para este problema fue descrita por primera vez por Nussinov en 1978.

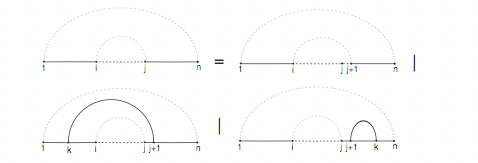
La intuición detrás de este algoritmo es la siguiente: dada una subsecuencia [i, j], o no hay borde que se conecte a la i-ésima base (lo que significa que está desapareada) o hay algún borde que conecte la i-ésima base a la base k donde i < k ≤ j (es decir, la i-ésima base está emparejada con la base késima). En el caso de que la i-ésima base no esté apareada, la energía de la subsecuencia, Ei, j, simplemente se reduce a la energía de la subsecuencia de i + 1 a j, Ei+1, j. Este es el primer término de la relación de recurrencia de Nussinov. Sin embargo, si la i-ésima base se empareja con la base késima, entonces Ei, j se reduce a la contribución de energía del emparejamiento i, k, βi, k, más la energía de las subsecuencias formadas dividiendo [i + 1, j] alrededor de k, Ei+1, k−1 y Ek+1, j. Al elegir la k que minimiza ese valor se obtiene el segundo término de la relación de recurrencia de Nussinov. La energía óptima de la subsecuencia, por lo tanto, es el mínimo de la energía de la subsecuencia cuando la i-ésima base se empareja con la base késima óptima y cuando la i-ésima base no está apareada. Esto produce la relación global descrita en la figura 10.8.

Figura 10.8: La fórmula de recursión para el algoritmo de Nussinov, junto con una representación gráfica de cómo funciona.

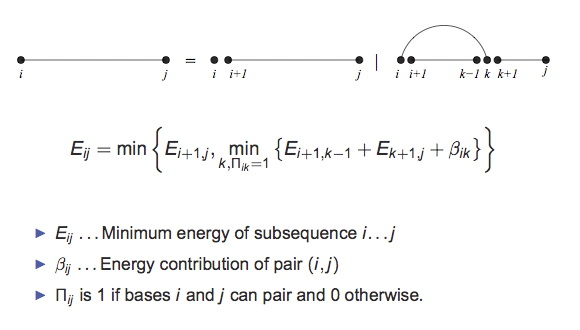
A partir de esta relación de recurrencia, podemos ver que la matriz DP contendrá entradas para todos i, j donde 1≤i≤nandi≤j≤NandnisthelengthofThernasEquence. Es decir, la matriz será n ∗ n y sólo contendrá entradas en el triángulo superior derecho. La matriz se inicializa primero de tal manera que todos los valores en la diagonal son iguales a cero. Luego iteramos sobre i = n − 1... 1... 1 y j = i + 1... n (abajo hacia arriba, de izquierda a derecha) y rellenamos cada entrada según la relación de recurrencia. La puntuación general es la puntuación de la subsecuencia [1, n], que es la esquina superior derecha de la matriz. La Figura 10.9 ilustra este procedimiento.

Cuando calculamos la energía mínima libre, muchas veces nos interesa el pliegue correspondiente. Para recuperar el pliegue óptimo del algoritmo DP, se utiliza una matriz de rastreo para almacenar punteros desde cada entrada hasta su entrada principal. La Figura 10.10 describe el algoritmo de retroceso.

Este modelo es muy simplista y hay algunas limitaciones al mismo. El algoritmo de Nussinov, tal como se implementa ingenuamente, no toma en cuenta algunos de los aspectos limitantes del plegamiento del ARN. Lo más importante es que no considera las interacciones de apilamiento entre pares vecinos, un factor vital (incluso más que los enlaces de hidrógeno) en el plegamiento del ARN. Figura 10.11

Por lo tanto, es deseable integrar factores biofísicos en nuestra predicción. Una mejora, por ejemplo, es asignar energías a las caras gráficas (elementos estructurales en la figura 10.12), en lugar de pares de bases simples. La energía total de la estructura se convierte entonces en la suma de las energías de las subestructuras. Las energías de apilamiento se pueden calcular fundiendo oligonucleótidos experimentalmente.

© Stefan Washietl. Todos los derechos reservados. Este contenido está excluido de nuestra licencia Creative Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use/.

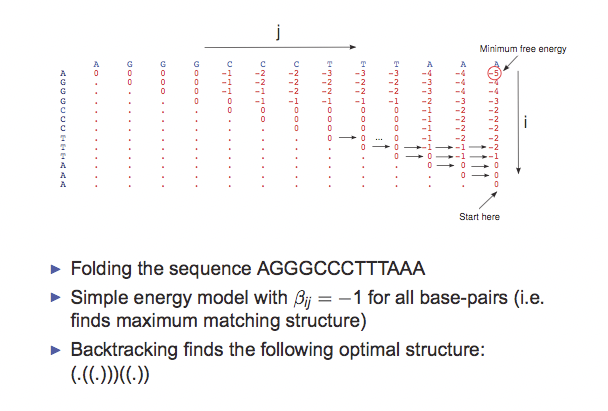
Figura 10.9: La diagonal se inicializa a 0. Luego, la tabla se llena de abajo hacia arriba, de izquierda a derecha ac- cording a la relación de recurrencia. En este ejemplo, los emparejamientos de bases complementarios se puntúan como -1 y los emparejamientos no complementarios se puntúan como 0. La puntuación óptima para toda la secuencia se encuentra en la esquina superior derecha.

© Stefan Washietl. Todos los derechos reservados. Este contenido está excluido de nuestra licencia Creative Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use/.

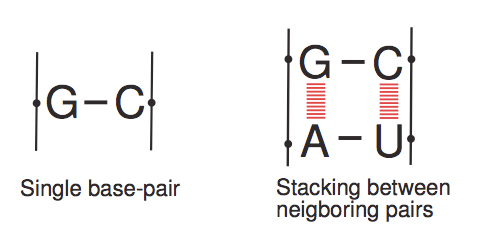
Figura 10.11: Apilamiento entre pares de bases vecinas en ARN. La estructura aromática plana de la base provoca interacciones cuánticas entre bases apiladas y cambia su estabilidad física.

Algoritmo Zuker

Por lo tanto, utilizamos una variante que incluye energías de apilamiento para calcular la estructura del ARN. A esto se le llama el algoritmo Zuker. Al igual que Nussinovs, asume que la estructura óptima es la que tiene la energía libre de equilibrio más baja. Sin embargo, incluye las contribuciones de energía total de las diversas subestructuras que está parcialmente determinada por la energía de apilamiento. Algunos algoritmos modernos de plegamiento de ARN utilizan este algoritmo para predicciones de estructura de ARN.

En el algoritmo de Zuker, tenemos cuatro casos diferentes que tratar. La Figura 10.13 muestra un esquema gráfico de las etapas de descomposición. El procedimiento requiere cuatro matrices. Fij contiene la energía libre de la estructura óptima global de la subsecuencia xij. La base recién agregada puede estar desemparejada o puede formar un par. Para

Figura 10.12: Varias subestructuras internas en un ARN plegado. Una horquilla consiste en un bucle terminal conectado a una región emparejada, un bucle interno es una región desapareada dentro de la región emparejada. Un Bulge es un caso especial de un bucle interior con un solo par erróneo. un Multi loop es un bucle que consiste en múltiples de estos componentes (en este ejemplo dos horquillas y una región emparejada, todas conectadas a un bucle). © Stefan Washietl. Todos los derechos reservados. Este contenido está excluido de nuestra licencia Creative Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use/.

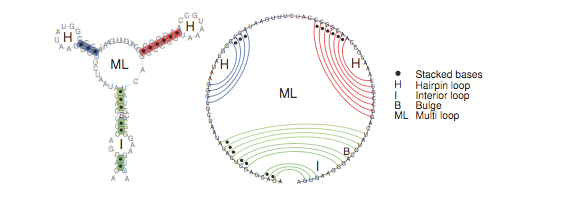
en este último caso, se introduce la matriz auxiliar C _ij, que contiene la energía libre de la subestructura óptima de x _ij bajo la restricción de que i y j están emparejados. Esta estructura cerrada por un par de bases puede ser una horquilla, un bucle interior o un bucle múltiple.

El caso de horquilla es trivial porque no es necesaria una mayor descomposición. La caja de bucle interior también es simple porque vuelve a reducir al mismo paso de descomposición. El paso multi-loop es más complicado. La energía de un bucle múltiple depende del número de componentes, es decir, subestructuras que emanan del bucle. Para realizar un seguimiento implícito de este número, se necesitan dos matrices auxiliares adicionales. M _ij mantiene la energía libre de la estructura óptima de x _ij bajo la restricción de que x _ij es parte de un bucle múltiple con al menos un componente. _Mij ¹ contiene la energía libre de la estructura óptima de x _ij bajo la restricción de que x _ij es parte de un multi-loop y tiene exactamente un componente cerrado por par (i, k) con i < k < j La idea es descomponer un bucle múltiple en dos partes arbitrarias de las cuales el primero es un multi-loop con al menos un componente y el segundo un multi-loop con exactamente un componente y comenzando con un par de bases.

Estas dos partes correspondientes a M y ^M1 pueden descomponerse adicionalmente en subestructuras que ya conocemos, es decir, intervalos desapareados, subestructuras cerradas por un par de bases, o multi-bucles (más cortos). (Las recursiones también se resumen en 10.13.

Figura 10.13: F describe el caso desapareado, C se describe por una de las tres condiciones: horquilla, bucle interior, o una composición de estructuras, es decir, un bucle múltiple. M1 es un bucle múltiple con un solo componente, donde M podría tener múltiples de ellos. El | icono es notación para “o”. © Stefan Washietl. Todos los derechos reservados. Este contenido está excluido de nuestra licencia Creative Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use/.

En realidad, sin embargo, a temperatura ambiente (o temperatura celular), el ARN no se encuentra realmente en un solo estado, sino que varía en un conjunto termodinámico de estructura. Los pares de bases pueden romper sus vínculos con bastante facilidad, y aunque podríamos encontrar un óptimo absoluto en términos de energía libre, podría darse el caso de que exista otra estructura subóptima que es muy diferente de lo que predijo e y que tiene un papel importante en la célula. Para solucionar el problema podemos calcular las probabilidades de pares de bases para obtener el conjunto de estructuras, y luego podemos tener una idea mucho mejor de cómo es probablemente la estructura del ARN. Para ello, utilizamos el factor Boltzman:

\[\operatorname{Prob}(\mathcal{S})=\frac{\exp (-\Delta G(\mathcal{S}) / R T)}{Z}\nonumber\]

Esto nos da la probabilidad de una estructura dada, en un sistema termodinámico. Necesitamos normalizar la temperatura usando la función de partición Z, que es la suma ponderada de todas las estructuras, en función de su factor de Boltzman:

\[z=\sum_{s} \exp (-\Delta G(\mathcal{S}) / R T)\nonumber\]

También podemos representar este conjunto gráficamente, usando una gráfica de puntos para visualizar las probabilidades del par base. Para calcular la probabilidad específica para un par base (i, j), necesitamos calcular la función de partición, que viene dada por la siguiente fórmula:

\[p_{i j}=\frac{\widehat{Z}_{i} Z_{i+1,-1} \exp \left(-\beta_{j} / R T\right)}{Z}\nonumber\]

Para calcular Z (la función de partición sobre toda la estructura), usamos la recursión similar al algoritmo de Nussinovs (conocido como algoritmo McCaskill) .La función de partición interna se calcula usando la fórmula:

\[Z_{i j}=Z_{i+1, j}+\sum_{i+1 \leq k \leq j \atop n_{k}=1} Z_{i+1, k-1} Z_{k+1, j} \exp \left(-\beta_{i k} / R T\right)\nonumber\]

Con cada una de las adiciones correspondientes a una división diferente en nuestra secuencia como ilustra la siguiente figura. Obsérvese que la suma se multiplica a las funciones de energía ya que se expresa como exponencial.

 

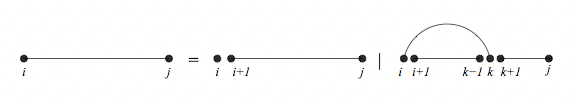
Del mismo modo, la función de partición externa se calcula con una misma idea usando la fórmula:

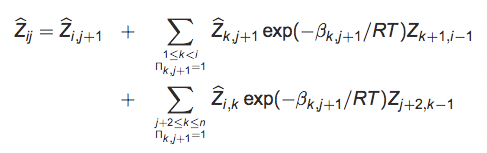
correspondientes a diferentes divisiones en el área fuera de los pares de bases (i, j).