17.3: Maximización de expectativas
- Page ID
- 54166
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La idea clave detrás de EM
Se nos da un conjunto de secuencias con el supuesto de que los motivos se enriquecen en ellas. La tarea es encontrar el motivo común en esas secuencias. La idea clave detrás de los siguientes algoritmos probabilísticos es que si se nos dieran posiciones iniciales de motivo en cada secuencia, encontrar el motivo PWM sería trivial; de manera similar, si se nos diera el PWM para un motivo particular, sería fácil encontrar las posiciones iniciales en las secuencias de entrada. Sea Z la matriz en la que Z ij corresponde a la probabilidad de que una instancia de motivo comience en la posición j en la secuencia i (en la Figura 17.8 se muestra un gráfico de las distribuciones de probabilidad resumidas en Z). Por lo tanto, estos algoritmos se basan en un enfoque iterativo básico: dada una longitud de motivo L y una matriz inicial Z, podemos usar las posiciones iniciales para estimar el motivo y, a su vez, usar el motivo resultante para reestimar las posiciones iniciales, iterando sobre estos dos pasos hasta la convergencia en un motivo.
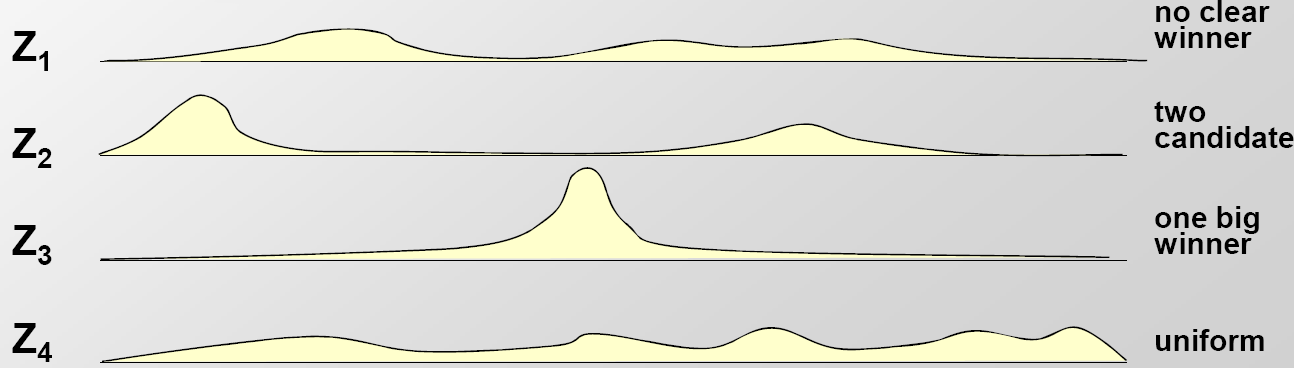
Figura 17.3: Ejemplos de la matriz Z calculada
El paso E: Estimación de Z ij a partir del PWM

Figura 17.4: Selección de la ubicación del motivo: el algoritmo codicioso siempre escogerá la ubicación más probable para el motivo. El algoritmo EM tomará un promedio mientras que Gibbs Sampling utilizará realmente la distribución de probabilidad dada por Z para muestrear un motivo en cada paso
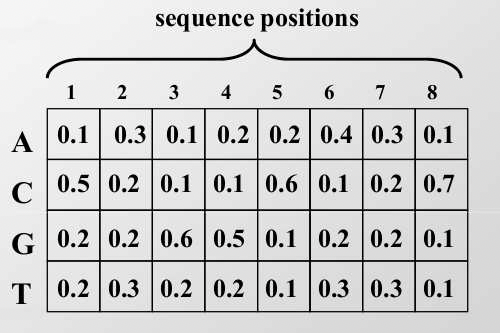
Paso 1: Inicialización El primer paso en EM es generar una matriz de ponderación de probabilidad inicial (PWM). El PWM describe la frecuencia de cada nucleótido en cada ubicación del motivo. En 17.5, hay un ejemplo de un PWM. En este ejemplo, asumimos que el motivo tiene ocho bases de largo.
Si se le da un conjunto de secuencias alineadas y la ubicación de motivos sospechosos dentro de ellas, entonces encontrar el PWM se logra calculando la frecuencia de cada base en cada posición del motivo sospechoso. Podemos inicializar el PWM eligiendo ubicaciones de inicio al azar.
Nos referimos al PWM como p ck, donde p ck es la probabilidad de que la base c ocurra en la posición k del motivo. Nota: si hay 0 probabilidad, generalmente es una buena idea insertar pseudo- recuentos en tus probabilidades. El PWM también se llama la matriz de perfil. Además del PWM, también mantenemos una distribución de fondo p ck, k=0, una distribución de las bases no en el motivo.
Paso 2: Expectativa En el paso de expectativa, generamos un vector Zij que contiene la probabilidad de que el motivo comience en la posición j en la secuencia i. En EM, el vector Z nos da una forma de clasificar todos los nucleótidos en las secuencias y decirnos si son parte del motivo o no. Podemos calcular Z ij usando la Regla de Bayes. Esto simplifica a:
\[ Z_{i j}^{t}=\frac{\operatorname{Pr}^{t}\left(X_{i} \mid Z_{i j}\right) \operatorname{Pr}^{t}\left(Z_{i j}=1\right)}{\Sigma_{k=1}^{L-W+1} \operatorname{Pr}^{t}\left(X_{i} \mid Z_{i j}=1\right) \operatorname{Pr}^{t}\left(Z_{i k}=1\right)} \nonumber \]
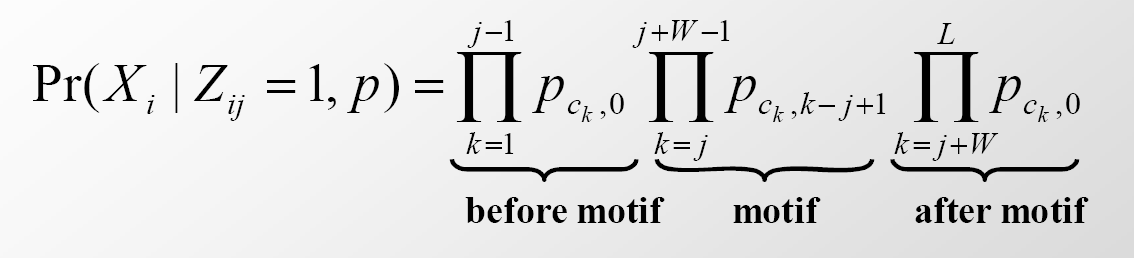
donde\(\operatorname{Pr}^{t}\left(X_{i} \mid Z_{i j}=1\right)=\operatorname{Pr}\left(X_{i} \mid Z_{i j}=1, p\right)\) se define como
Esta es la probabilidad de secuencia i dado que el motivo comienza en la posición j. El primer y último producto corresponden a la probabilidad de que las secuencias que preceden y siguen al motivo candidato provengan de alguna distribución de probabilidad de fondo mientras que el producto medio corresponde a la probabilidad que la instancia de motivo candidato vino de una distribución de probabilidad de motivo. En esta ecuación, asumimos que la secuencia tiene longitud L y el motivo tiene longitud W.
paso: Encontrar el motivo de máxima verosimilitud desde las posiciones iniciales Zij
Paso 3: Maximización Una vez que hemos calculado Zt, podemos usar los resultados para actualizar tanto el PWM como la distribución de probabilidad de fondo. Podemos actualizar el PWM usando la siguiente ecuación
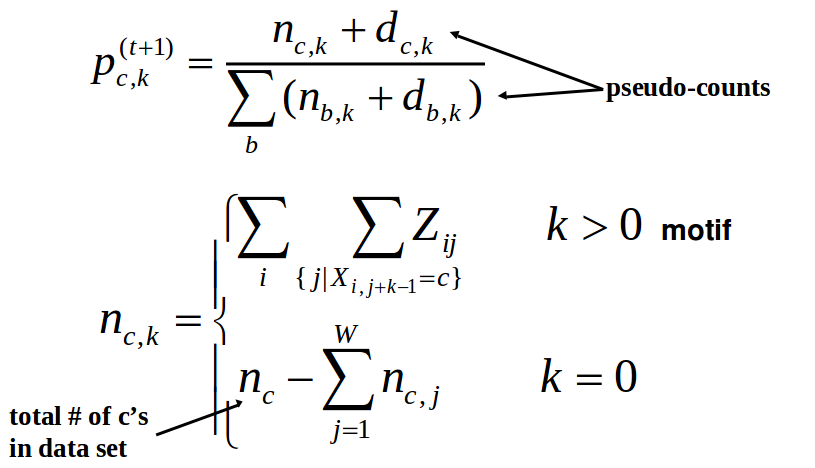
Paso 4: Repita Repita los pasos 2 y 3 hasta la convergencia.
Una forma posible de probar si la matriz de perfil ha convergido es medir cuánto cambia cada elemento en el PWM después de la maximización de pasos. Si el cambio está por debajo de un umbral elegido, entonces podemos terminar el algoritmo. EM es un algoritmo determinista y depende completamente de los puntos de partida iniciales porque utiliza un promedio sobre la distribución de probabilidad completa. Por lo tanto, es recomendable volver a ejecutar el algoritmo con diferentes posiciones iniciales iniciales para intentar reducir la posibilidad de converger sobre un máximo local que no sea el máximo global y para tener una buena idea del espacio de solución.


