21.6: Clustering de redes, Bibliografía

Última actualización
Guardar como PDF

Page ID: 54996

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

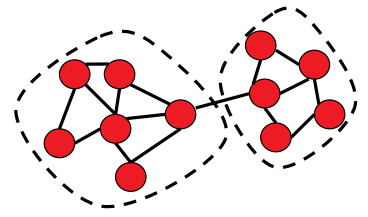
Un problema importante en el análisis de redes es poder agrupar o modular la red para identificar subgrafos que están densamente conectados (ver por ejemplo, la figura 21.6a). En el contexto de las redes de interacción génica, estos conglomerados podrían corresponder a genes que están involucrados en funciones similares y que están co-regulados.

Existen varios algoritmos conocidos para lograr esta tarea. Estos algoritmos suelen denominarse algoritmos de particionamiento gráfico ya que particionan el gráfico en módulos separados. Algunos de los algoritmos conocidos incluyen:

Algoritmo de agrupamiento de Markov [5]: El Algoritmo de Clustering de Markov (MCL) funciona haciendo una caminata aleatoria en la gráfica y observando la distribución en estado estacionario de esta caminata. Esta distribución en estado estacionario permite agrupar la gráfica en subgrafías densamente conectadas.
Algoritmo Girvan-Newman [2]: El algoritmo Girvan-Newman utiliza el número de rutas más cortas que pasan por un nodo para calcular la esencialidad de un borde que luego se puede usar para agrupar la red.
Algoritmo de partición espectral

En esta sección veremos en detalle el algoritmo de particionamiento espectral. Referimos al lector a las referencias [2, 5] para una descripción de los otros algoritmos.

El algoritmo de partición espectral se basa en una cierta forma de representar una red usando una matriz. Antes de presentar el algoritmo revisaremos así cómo representar una red usando una matriz, y cómo extraer información sobre la red usando operaciones matriciales.

a) Una partición de una red en dos grupos.

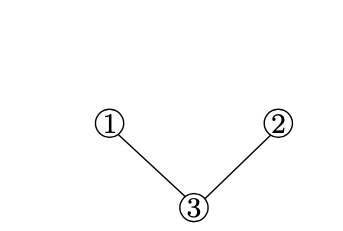
Screen Shot 2020-09-14 at 11.16.02 AM.png — b) Una red simple en 3 nodos. La adyacencia
matriz de esta gráfica se da en la ecuación (21.1).

Figura 21.6

Vista algebraica a las redes

Matriz de adyacencia Una forma de representar una red es usar la llamada matriz de adyacencia. La matriz de adyacencia de una red con n nodos es una matriz\(\times\) N N A donde A _{i, j} es igual a uno si hay un borde entre los nodos i y j, y 0 en caso contrario. Por ejemplo, la matriz de adyacencia del gráfico representado en la figura 21.6b viene dada por:

\ [A=\ left [\ begin {array} {lll}
0 & 0 & 1\\
0 & 0 & 1\\
1 & 1 & 0 & 0
\ end {array}\ derecha]\ nonumber\]

Si la red está ponderada (es decir, si los bordes de la red tienen cada uno un peso asociado), la definición de la matriz de adyacencia se modifica para que Ai, j mantenga el peso del borde entre i y j si el borde existe, y cero en caso contrario.

Matriz laplaciana Para el algoritmo de clustering que presentaremos más adelante en esta sección, necesitaremos contar el número de bordes entre los dos grupos diferentes en una partición de la red. Por ejemplo, en la Figura 21.6a, el número de aristas entre los dos grupos es de 1. La matriz laplaciana que vamos a introducir ahora es útil para representar esta cantidad algebraicamente. La matriz laplaciana L de una red en n nodos es una matriz n\(\times\) n L que es muy similar a la matriz de adyacencia A excepto por los cambios de signo y para los elementos diagonales. Mientras que los elementos diagonales de la matriz de adyacencia son siempre iguales a cero (ya que no tenemos auto-bucles), los elementos diagonales de la matriz Laplaciana mantienen el grado de cada nodo (donde el grado de un nodo se define como el número de aristas que inciden en él). También los elementos fuera de la diagonal de la matriz laplaciana se establecen en 1 en presencia de un borde, y cero en caso contrario. En otras palabras, tenemos:

\ [L_ {i, j} =\ left\ {\ begin {array} {ll}
\ operatorname {degree} (i) &\ text {if} i=j\\
-1 &\ text {if} i\ neq j\ text {y hay un borde entre} i\ text {y} j\\
0 &\ text {if} i\ neq j\ text {y no hay borde entre} i\ texto {y} j
\ end {array}\ derecho. \ nonumber\]

Por ejemplo, la matriz laplaciana de la gráfica de la figura 21.6b viene dada por (enfatizamos los elementos diagonales en negrita):

\ [L=\ left [\ begin {array} {ccc}
1 & 0 & -1\\
0 & 1 & -1\\
-1 & -1 & 2
\ end {array}\ derecha]\ nonumber\]

Algunas propiedades de la matriz laplaciana La matriz laplaciana de cualquier red disfruta de algunas propiedades agradables que serán importantes más adelante cuando veamos el algoritmo de clustering. Revisamos brevemente estos aquí.

La matriz laplaciana L es siempre simétrica, es decir, Li, j = Lj, i para cualquier i, j. Una consecuencia importante de esta observación es que todos los valores propios de L son reales (es decir, no tienen parte imaginaria compleja). De hecho incluso se puede demostrar que los valores propios de L son todos no negativos8 La propiedad final que mencionamos sobre L es que todas las filas y columnas de L suman a cero (esto es fácil de verificar usando la definición de L). Esto significa que el valor propio más pequeño de L es siempre igual a cero, y el vector propio correspondiente es s = (1,1,... ,1).

Contando el número de aristas entre grupos usando la matriz Laplaciana Usando la matriz laplaciana ahora podemos contar fácilmente el número de aristas que separan dos partes disjuntas de la gráfica usando operaciones simples de matriz. En efecto, supongamos que particionamos nuestra gráfica en dos grupos, y que definimos un vector s de tamaño n que nos dice a qué grupo pertenece cada nodo i:

\ [s_ {i} =\ left\ {\ begin {array} {ll}
1 &\ text {if node} i\ text {está en el grupo} 1\\
-1 &\ text {if node} i\ text {está en el grupo} 2
\ end {array}\ right. \ nonumber\]

Entonces se puede demostrar fácilmente que el número total de aristas entre el grupo 1 y el grupo 2 viene dado por la cantidad\(\frac{1}{4} s^{T}\) Ls donde L es el laplaciano de la red.

Para ver por qué este es el caso, primero calculemos el producto matriz-vector Ls. En particular, fijemos un nodo que digo en el grupo 1 (es decir, si = +1) y veamos el componente i'ésimo del producto matriz-vector Ls. Por definición del producto matriz-vector tenemos:

\[(L s)_{i}=\sum_{j=1}^{n} L_{i, j} s_{j} \nonumber \]

Podemos descomponer esta suma en tres summands de la siguiente manera:

\[(L s)_{i}=\sum_{j=1}^{n} L_{i, j} s_{j}=L_{i, i} s_{i}+\sum_{j \text { in group } 1} L_{i, j} s_{j}+\sum_{j \text { in group } 2} L_{i, j} s_{j} \nonumber \]

Usando la definición de la matriz Laplaciana vemos fácilmente que el primer término corresponde al grado de i, es decir, el número de aristas incidentes a i; el segundo término es igual al negativo del número de aristas que conectan i a algún otro nodo del grupo 1, y el tercer término es igual al número de aristas que conectan i a algún nodo ingroup 2. De ahí que tengamos:

(Ls) _i = grado (i) (# bordes de i al grupo 1) + (# bordes de i al grupo 2)

Ahora como cualquier borde de i debe ir al grupo 1 o al grupo 2 tenemos:

grado (i) = (# bordes de i al grupo 1) + (# bordes de i al grupo 2).

Así combinando las dos ecuaciones anteriores obtenemos:

(Ls) _i = 2 (# bordes de i al grupo 2).
Ahora para obtener el número total de aristas entre el grupo 1 y el grupo 2, simplemente sumamos la cantidad anterior

sobre todos los nodos i del grupo 1:
\[\text { (# edges between group 1 and group 2) }=\frac{1}{2} \sum_{i \text { in group } 1}(L s)_{i} \nonumber\]

También podemos mirar nodos en el grupo 2 para calcular la misma cantidad y tenemos:

\[\text { (# edges between group 1 and group 2) }=-\frac{1}{2} \sum_{i \text { in group 2 }}(L s)_{i} \nonumber \]

Ahora promediando las dos ecuaciones anteriores obtenemos el resultado deseado:

\ [\ begin {alineado}
&\ text {(# bordes entre el grupo 1 y el grupo 2)} =\ frac {1} {4}\ sum_ {i\ text {en el grupo 1}} (L s) _ {i} -\ frac {1} {4}\ sum_ {i\ text {en el grupo 2}} (L s) _ {i}\\
&\ begin {array} {l}
=\ frac {1} {4}\ suma_ {i} s_ {i} (L s) _ {i}\\
=\ frac {1} {4} s^ {T } L s
\ end {array}
\ end {alineado}\ nonumber\]

donde sT es el vector de fila obtenido al transponer el vector de columna s.

El algoritmo de agrupamiento espectral

Ahora veremos cómo se puede utilizar la vista de álgebra lineal de las redes dada en la sección anterior para producir una “buena” partición de la gráfica. En cualquier buena partición de una gráfica, el número de aristas entre los dos grupos debe ser relativamente pequeño en comparación con el número de aristas dentro de cada grupo. Así, una forma de abordar el problema es buscar una partición para que el número de aristas entre los dos grupos sea mínimo. Utilizando las herramientas introducidas en la sección anterior, este problema es así equivalente a encontrar un vector\(s \in\{-1,+1\}^{n}\) tomando solo valores 1 o +1 tal que\(\frac{1}{4} s^{T}\) Ls sea mínimo, donde L es la matriz Laplaciana de la gráfica. En otras palabras, queremos resolver el problema de minimización:

\(\operatorname{minimize}_{s \in\{-1,+1\}^{n}} \frac{1}{4} s^{T} L s \nonumber \)

Si s ^* es la solución óptima, entonces la partición óptima es asignar el nodo i al grupo 1 si s _i = +1 o bien al grupo 2.

Esta formulación parece tener sentido pero desafortunadamente hay una pequeña falla: la solución a este problema siempre terminará siendo s = (+1,..., +1) lo que corresponde a poner todos los nodos de la red en el grupo 1, ¡y ningún nodo en el grupo 2! El número de aristas entre el grupo 1 y el grupo 2 es entonces simplemente cero y, de hecho, ¡es mínimo!

Para obtener una partición significativa tenemos que considerar así particiones de la gráfica que no son triviales. Recordemos que la matriz laplaciana L es siempre simétrica, y así admite una descomposición propia:

\[L=U \Sigma U^{T}=\sum_{i=1}^{n} \lambda_{i} u_{i} u_{i}^{T}\nonumber\]

donde\(\sigma\) es una matriz diagonal que contiene los valores eigen no negativos\(\lambda_{1}, \ldots, \lambda_{n}\) de L y U es la matriz de vectores propios y satisface U ^T =U- ¹.

El costo de una partición\(s \in\{-1,+1\}^{n}\) viene dado por

\[\frac{1}{4} s^{T} L s=\frac{1}{4} s^{T} U \Sigma U^{T} s=\frac{1}{4} \sum_{i=1}^{n} \lambda_{i} \alpha_{i}^{2}\nonumber\]

donde\(\alpha=U^{T}s\) dan la descomposición de s como una combinación lineal de los vectores propios de L:\(s=\sum_{i=1}^{n} \alpha_{i} u_{i}\).

fuente desconocida. Todos los derechos reservados. Este contenido está excluido de nuestro Creativo
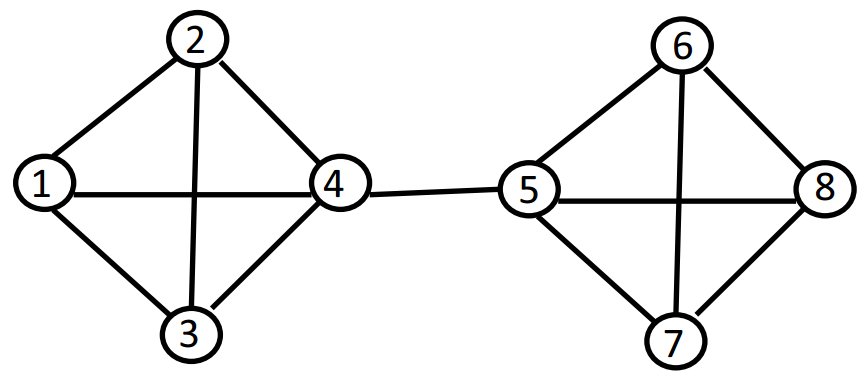
Licencia Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use/.

Figura 21.7: Una red con 8 nodos

Recordemos también eso\(0=\lambda_{1} \leq \lambda_{2} \leq \cdots \leq \lambda_{n}\). Así, una forma de hacer que la cantidad anterior sea lo más pequeña posible (sin escoger la partición trivial) es concentrar todo el peso sobre el\(\lambda_{2}\) que se encuentra el valor propio más pequeño distinto de cero de L. Para lograr esto simplemente elegimos s de manera que\(\alpha_{2}\) =1 y\(\alpha_{k}\) = 0 para todos k\(\neq\) 2. En otras palabras, esto corresponde a tomar s para que sea igual a u ₂ el segundo vector propio de L. Dado que en general el autovector u ₂ no tiene valor entero (es decir, los componentes de u ₂ pueden ser diferentes a 1 o +1), tenemos que convertir primero el vector _u2 en un vector de +1 o 1's Una forma sencilla de hacer esto es solo mirar los signos de los componentes de u ₂ en lugar de los valores mismos. Nuestra partición está así dada por:

\ [s=\ operatorname {signo}\ left (u_ {2}\ right) =\ left\ {\ begin {array} {ll}
1 &\ text {if}\ left (u_ {2}\ right) _ {i}\ geq 0\\
-1 &\ text {if}\ left (u_ {2}\ right) _ {i} <0
\ end {array} derecha\. \ nonumber\]

Para recapitular, el algoritmo de agrupamiento espectral funciona de la siguiente manera:

Algoritmo de partición espectral

Entrada: una red
Salida: una partición de la red donde cada nodo está asignado ya sea al grupo 1 o al grupo
2 para que el número de aristas entre los dos grupos sea pequeño

Calcular la matriz Laplaciana L de la gráfica dada por:
\ [L_ {i, j} =\ left\ {\ begin {array} {ll}
\ operatorname {degree} (i) &\ text {if} i=j\\
-1 &\ text {if} i\ neq j\ text {y hay un borde entre} i\ text {y} j\\
0 &\ text {if} i\ neq j\ text {y no hay borde entre} i\ texto { y} j
\ end {array}\ right. \ nonumber\]
Calcular el autovector u ₂ para el segundo valor propio más pequeño de L.
Salida de la siguiente partición: Asignar nodo i al grupo 1 if (u ₂) _i\(\geq\) 0, de lo contrario asignar el nodo i al grupo 2.

A continuación damos un ejemplo donde aplicamos el algoritmo de clustering espectral a una red con 8 nodos.

Ejemplo Ilustramos aquí el algoritmo de particionamiento descrito anteriormente en una red simple de 8 nodos dado en la figura 21.7. La matriz de adyacencia y la matriz Laplaciana de esta gráfica se dan a continuación:

\ [A=\ left [\ begin {array} {llllllll}
0 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 &
1 & 0 & 0 & 0 & 0 & 0 & 0 &
1 & 1 & 0 & 1 & 0 & 1 &
amp; 0 & 0 & 0\\
0 & 0 & 1 & 0 & 1 & 1 & 1 & 1\\
0 & 0 & 0 & 0 & 1 & 0 & 1 & 1 &
0 & 1 & 1 & 1 & 0 & 1 & 0 & 1 &
0 & 1\\ 0 & 0 & 0 & 1 & amp; 1 & 0
\ end {array}\ derecha]\ quad L=\ izquierda [\ begin {array} {rrrrrr}
3 & -1 & -1 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 &
1 & 3 & 0 & 0 & -1 & 0 & 0 & 0
& 0\\
-1 y -1 & 4 & -1 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 0 & -1 & 1 & -1 & -1 & -1 & 0 & 0 & 0 & -1 & -1 & -1 & -1\\
0 & 0 & 0 & 0 & -1 &
amp; 3 & -1\\
0 & 0 & 0 & 0 & -1 & -1 & -1 & 3
\ end {array}\ right]\ nonumber\]
Usando el comando eig de Matlab podemos calcular la descomposición propia\(L=U \Sigma U^{T}\) de la matriz Laplaciana y obtenemos:

\ [U=\ left [\ begin {array} {rrrrrrr}
0.3536 & -0.3825 & 0.2714 & -0.1628 & -0.7783 & 0.0495 & -0.0064 & -0.1426\\
0.3536 & -0.3825 & 0.5580 & -0.1628 & 0.6066 & 0.0495 & -0.0064 & -0.1426\\
0.3536 & -0.3825 & ; -0.4495 & 0.6251 & 0.0930 & 0.0495 & -0.3231 & -0.1426\\
0.3536 & -0.2470 & -0.3799 & -0.2995 & 0.0786 & -0.1485 & 0.3358 & 0.6626\\
0.3536 &\ mathbf {0. 2 4 7 0} & -0.3799 & -0.2995 & 0.0786 & -0.1485 & 0. 3358 & -0.6626\\
0.3536 &\ mathbf {0. 3 8 2 5} & 0.3514 & 0.5572 & -0.0727 & -0.3466 & 0.3860 & 0.1426\\
0.3536 &\ mathbf {0. 3 8 2 5} & 0.0284 & -0.2577 & -0.0059 & -0.3466 & -0.7218 & 0.1426\\
0.3536 & ;\ mathbf {0. 3 8 2 5} & 0.0000 & 0.0000 & 0.0000 & 0.8416 & -0.0000 & 0.1426
\ end {array}\ derecho]\ nonumber\]

\ [\ Sigma=\ left [\ begin {array} {llllllll}
0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0\\ 0 & 0.3542 & 0 &
0 & 0 & 0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & ; 4.0000 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 0 & 0 & 0 &
0 & 0 & 0 & 0 & 0 & 0 &
0 & 0 & amp; 0 & 0 & 0 & 0 & 0 & 5.6458
\ end {array}\ derecha]\ nonumber\]

Hemos resaltado en negrita el segundo valor propio más pequeño de L y el autovector asociado. Para agrupar la red observamos el signo de los componentes de este vector propio. Vemos que los primeros 4 componentes son negativos, y los últimos 4 componentes son positivos. Así, agruparemos los nodos 1 a 4 juntos en el mismo grupo, y los nodos 5 a 8 en otro grupo. Esto parece un buen agrupamiento y de hecho esta es la agrupación “natural” que se considera a primera vista de la gráfica.

¿Sabías?

El problema matemático que formulamos como motivación para el algoritmo de agrupamiento espectral es encontrar una partición de la gráfica en dos grupos con un número mínimo de bordes entre los dos grupos. El algoritmo de particionamiento espectral que presentamos no siempre da una solución óptima a este problema pero suele funcionar bien en la práctica.

En realidad resulta que el problema tal y como lo formulamos se puede resolver exactamente usando un algoritmo eficiente. El problema a veces se llama el problema de corte mínimo ya que estamos buscando cortar un número mínimo de bordes de la gráfica para desconectarla (los bordes que cortamos son los que se encuentran entre el grupo 1 y el grupo 2). El problema de corte mínimo se puede resolver en tiempo polinomial en general, y remitimos al lector a la entrada de Wikipedia sobre corte mínimo [9] para más información. El problema sin embargo con las particiones de corte mínimo es que generalmente conducen a particiones de la gráfica que no están equilibradas (por ejemplo, un grupo tiene solo 1 nodo, y los nodos restantes están todos en el otro grupo). En general, uno quisiera imponer restricciones adicionales a los clústeres (por ejemplo, límites inferiores o superiores en el tamaño de los clústeres, etc.) para obtener clústeres más realistas. Con tales limitaciones, el problema se vuelve más difícil, y remitimos al lector a la entrada de Wikipedia sobre Particionamiento gráfico [8] para más detalles.

Preguntas frecuentes

P: ¿Cómo dividir la gráfica en más de dos grupos?

R: En esta sección solo nos fijamos en el problema de particionar la gráfica en dos clústeres. ¿Y si queremos agrupar la gráfica en más de dos clústeres? Hay varias extensiones posibles del algoritmo que se presentan aquí para manejar k clústeres en lugar de solo dos. La idea principal es mirar los k vectores propios para los k valores propios distintos de cero más pequeños del Laplaciano, y luego aplicar el algoritmo de clustering k-means apropiadamente. Refirimos al lector al tutorial [7] para más información.

⁸ Una forma de ver esto es notar que L es diagonalmente dominante y los elementos diagonales son estrictamente positivos (para más detalles el lector puede buscar “diagonalmente dominante” y “teorema del círculo Gershgorin” en Internet).