26.2: Fundamentos de la Filogenia
- Page ID
- 53968
Árboles
Un árbol es una representación matemática de las relaciones entre objetos. Un árbol general se construye a partir de nodos y bordes. Cada nodo representa un objeto, y cada borde representa una relación entre dos nodos. En el caso de los árboles filogenéticos, representamos la evolución utilizando árboles. En este caso, cada nodo representa un evento de divergencia entre dos linajes ancestrales, las hojas denotan el conjunto de objetos presentes y la raíz representa al ancestro común.
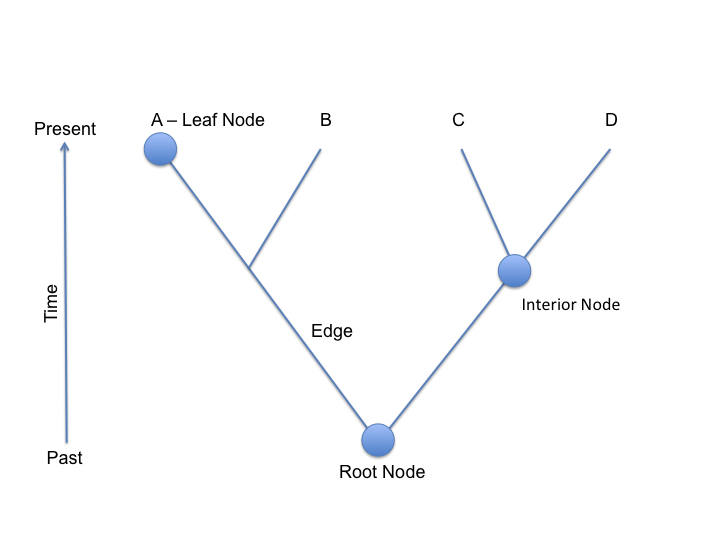
Sin embargo, a veces se refleja más información en las longitudes de las ramas, como el tiempo transcurrido o la cantidad de disimilitud. Según estas dierencias, los árboles filogenéticos biológicos pueden clasificarse en tres categorías:
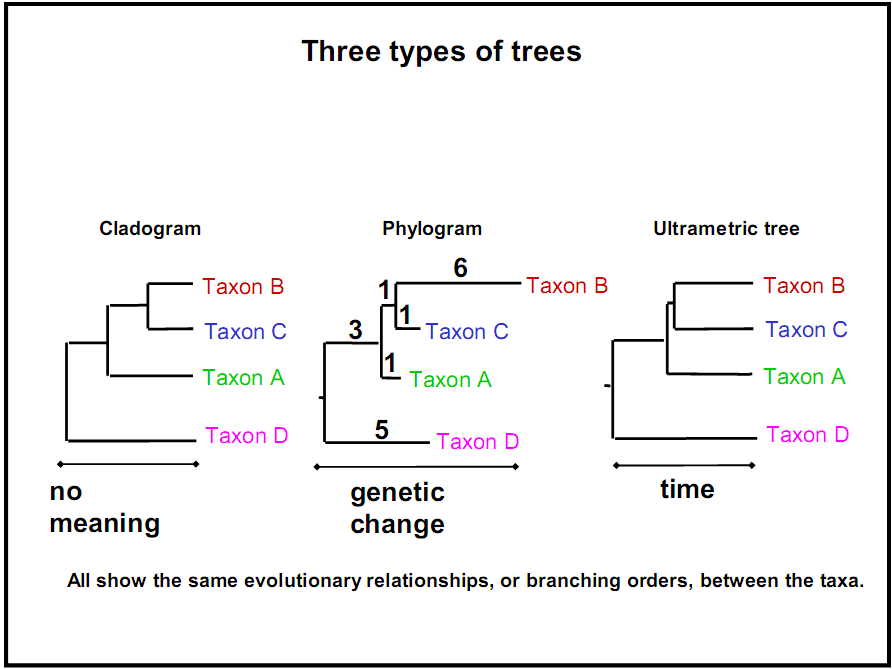
Cladograma: no da sentido a las longitudes de ramificación; solo importa la secuencia y topología de la ramificación.
Filograma: Las longitudes de las ramas están directamente relacionadas con la cantidad de cambio genético. Cuanto más larga es la rama de un árbol, mayor es la cantidad de cambio filogenético que ha tenido lugar. Las hojas de este árbol no necesariamente terminan en la misma línea vertical, debido a diferentes tasas de mutación.
Cronograma (árbol ultramétrico): Las longitudes de las ramas están directamente relacionadas con el tiempo. Cuanto más largas sean las ramas de un árbol, mayor será la cantidad de tiempo que ha pasado. Las hojas de este árbol necesariamente terminan en la misma línea vertical (es decir, están a la misma distancia de la raíz), ya que todas están presentes a menos que se incluyan especies extintas en el árbol. Aunque existe una correlación entre las longitudes de las ramas y la distancia genética en un cronograma, no son necesariamente exactamente proporcionales porque las tasas de evolución/tasas de mutación no son constantes. Algunas especies evolucionan y mutan más rápido que otras, y algunos períodos históricos fomentan tasas de evolución más rápidas que otras.
Un rasgo es cualquier característica que posea un objeto o especie. En los humanos, un ejemplo de un rasgo puede ser el bipedalismo (la capacidad de caminar erguido) o el pulgar oponible. Otro rasgo humano puede ser una secuencia de ADN específica que poseen los humanos. Los primeros ejemplos de rasgos físicos se denominan rasgos morfológicos, mientras que los últimos rasgos de ADN se denominan rasgos de secuencia. Cada uno tiene sus ventajas y desventajas para estudiar. Todos los métodos para la reconstrucción arbórea se basan en el estudio de la ocurrencia de rasgos dierentes en los objetos dados. En la filogenética tradicional se utilizaron los datos morfológicos de diferentes especies para este propósito. En los métodos modernos, se utilizan datos de secuencias genéticas en su lugar. Cada uno tiene sus ventajas y desventajas.
Rasgos morfológicos: Surgen de la evaluación empírica de los rasgos físicos. Esto puede ser ventajoso porque las características físicas son muy fáciles de cuantificar y entender para todos, científicos y niños por igual. Las desventajas de este enfoque son que solo podemos evaluar un pequeño conjunto de rasgos, como pelo, uñas, pezuñas, dientes, etc. Además, estos rasgos solo nos permiten construir especies. Por último, es mucho más fácil ser “engañado” por la evolución convergente. Las especies que divergieron hace millones de años pueden volver a converger en los pocos rasgos que son observables para los científicos, dando una falsa representación de cuán estrechamente relacionadas están las especies.
Rasgos de Secuencia: Se descubren mediante el estudio de los genomas de diferentes especies. Este enfoque puede ser ventajoso porque crea muchos más datos y permite a los científicos crear árboles genéticos además de árboles de especies. La principal dificultad con este enfoque es que el ADN solo se construye a partir de 4 bases, por lo que las retromutaciones son frecuentes. En este enfoque, los científicos deben conciliar las señales de un gran número de rasgos de mal comportamiento frente a la de un pequeño número de rasgos de buen comportamiento en el enfoque tradicional. El resto del capítulo se centrará principalmente en la construcción de árboles a partir de secuencias génicas.
Dado que este enfoque trata de comparar entre pares de genes, es útil entender el concepto de homología: Un par de genes se llaman parálogos si divergieron de un evento de duplicación, y ortólogos si divergieron de un evento de especiación.
Preguntas frecuentes
P: ¿Sería posible utilizar secuencias de ADN de especies extintas?
R: Las tecnologías actuales solo permiten el uso de secuencias existentes. Sin embargo, ha habido algunos éxitos en el uso del ADN de especies extintas. El ADN de mamuts congelados ha sido recolectado y están siendo secuencias pero debido a que el ADN se descompone con el tiempo y la contaminación del ambiente, es muy difícil extraer secuencias correctas.
Una vez que hemos encontrado datos genéticos para un conjunto de especies, nos interesa conocer cómo esas especies se relacionan entre sí. Dado que en su mayor parte solo podemos obtener ADN de criaturas vivientes, debemos inferir la existencia de ancestros de cada especie, y en última instancia inferir la existencia de un ancestro común. Este es un problema desafiante, porque se dispone de datos muy limitados. Las siguientes secciones explorarán los métodos modernos para inferir ascendencia a partir de datos de secuencia. Se pueden clasificar en dos enfoques, métodos basados en distancia y métodos basados en caracteres.
Los enfoques basados en la distancia toman dos pasos para resolver el problema, es decir, cuantificar la cantidad de mutación que separa cada par de secuencias (que puede o no ser proporcional al tiempo transcurrido desde que se han separado) y ajustar el árbol más probable de acuerdo con la matriz de distancia por pares. El segundo paso suele ser un algoritmo directo, basado en algunas suposiciones, pero puede ser más complejo.
En cambio, los enfoques basados en caracteres intentan encontrar el árbol que mejor explique las secuencias observadas. A diferencia de la reconstrucción directa, estos métodos se basan en la propuesta de árboles y técnicas de puntuación para realizar una búsqueda heurística sobre el espacio de los árboles.
¿Sabías?
La navaja de Occam, como se discutió en capítulos anteriores, no siempre proporciona la hipótesis más precisa. En muchos casos durante la reconstrucción arbórea, la explicación más simple no es la más probable. Por ejemplo, puede ser posible un conjunto de posibles ancestros, dados algunos datos observados. En este caso, la ascendencia más simple puede no ser correcta si un rasgo surgió independientemente en dos linajes separados. Este tema será considerado en una sección posterior.

