26.3: Métodos basados en la distancia
- Page ID
- 53921
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Los modelos basados en distancia secuestran los datos de secuencia en distancias por pares. Este paso pierde algo de información, pero establece la plataforma para la reconstrucción directa de árboles. Las dos etapas de este método se discuten en detalle en la presente memoria.
De la alineación a las distancias
Para entender cómo funciona un modelo basado en la distancia, es importante pensar qué significa distancia al comparar dos secuencias. Hay tres interpretaciones principales.
La divergencia de nucleótidos es la idea de medir la distancia entre dos secuencias en función del número de lugares donde los nucleótidos no son consistentes. Esto supone que la evolución ocurre a una velocidad uniforme en todo el genoma, y que un nucleótido dado es igual de probable que evolucione hacia cualquiera de los otros tres nucleótidos. A pesar de que tiene deficiencias, esta suele ser una excelente manera de pensarlo.
Transiciones y Transversiones Esto es similar a la divergencia de nucleótidos, pero reconoce que las sustituciones A-G y T-C son las más frecuentes. Por lo tanto, mantiene dos parámetros, la probabilidad de una transición y la probabilidad de una transversión.
Sustituciones sinónimas y no sinónimas Este método mantiene un seguimiento de las sustituciones que afectan al aminoácido codificado asumiendo que las sustituciones que no cambian la proteína codificada no se seleccionarán contra, y por lo tanto tendrán una mayor probabilidad de ocurrir que aquellas sustituciones que cambien el aminoácido codificado.
La forma ingenua de interpretar la separación entre dos secuencias puede ser simplemente el número de desapareamientos, como se describe por la divergencia de nucleótidos anteriormente. Si bien esto nos proporciona una métrica de distancia (es decir, d (a, b) + d (b, c) d (a, c)) esto no satisface del todo nuestros requisitos, porque queremos distancias aditivas, es decir, aquellas que satisfacen d (a, b) + d (b, c) = d (a, c) para un camino a! b! c de secuencia evolutiva, porque la cantidad de mutaciones acumuladas a lo largo de un camino en el árbol debe ser la suma de la de sus componentes individuales. Sin embargo, la fracción de desajuste ingenuo no siempre tiene esta propiedad, ya que esta cantidad está limitada por 1, mientras que la suma de componentes individuales puede superar fácilmente 1.
La clave para resolver esta paradoja son las retromutaciones. Cuando un gran número de mutaciones se acumulan en una secuencia, no todas las mutaciones introducen nuevos desapareamientos, algunas de ellas pueden ocurrir en un par de bases ya mutado, dando como resultado que la puntuación de desapareamientos permanezca igual o incluso decreciente. Sin embargo, para pequeñas puntuaciones de desajuste, este eect es estadísticamente insignificante, porque hay muchísimo más pares idénticos que pares descoincidentes. Sin embargo, para secuencias separadas por mayor distancia evolutiva, debemos corregir este efecto. El modelo Jukes-Cantor es uno de esos modelos de markov simples que toma esto en cuenta.
Distancias Jukes-Cantor
Para ilustrar este concepto, considere un nucleótido en estado 'A' en el tiempo cero. En cada paso de tiempo, tiene una probabilidad 0.7 de retener su estado previo y probabilidad 0.1 de transición a cada uno de los otros tres estados. La probabilidad P (B|t) de observar el estado (base) B en el tiempo t sigue esencialmente a la recursión
\[P(B \mid t+1)=0.7 P(B \mid t)+0.1 \sum_{b \neq B} P(b \mid t)=0.1+0.6 P(B \mid t)\nonumber\]
Figura 26.5: Cadena de Markov que da cuenta de las mutaciones de espalda
Si trazamos P (B|t) frente a t, observamos que la distribución comienza como concentrada en el estado 'A' y gradualmente se extiende al resto de los estados, yendo eventualmente hacia un equilibrio de probabilidades iguales. Esta progresión tiene sentido, intuitivamente. A lo largo de millones de años, las especies pueden evolucionar tan dramáticamente que ya no se parecen a sus antepasados. En ese extremo, una ubicación base dada en el antepasado es igual de probable que haya evolucionado a cualquiera de las cuatro bases posibles en esa ubicación a lo largo del tiempo.
\ [\ begin {array} {lccccr}
\ text {time: -} & 0 & 1 & 2 & 3 & 4\
\ hline\ text {A} & 1 & 0.7 & 0.52 & 0.412 & 0.3472\
\ text {C} & 0 & 0.1 & 0.16 & 0.196 & 0.2196\
\ text {G} & 0 & 0.1 & 0.16 & 0.196 & 0.2196\\
\ text {T} & 0 & 0.1 & 0.16 & 0.196 & 0.2196
\ end {array}\ nonumber\]
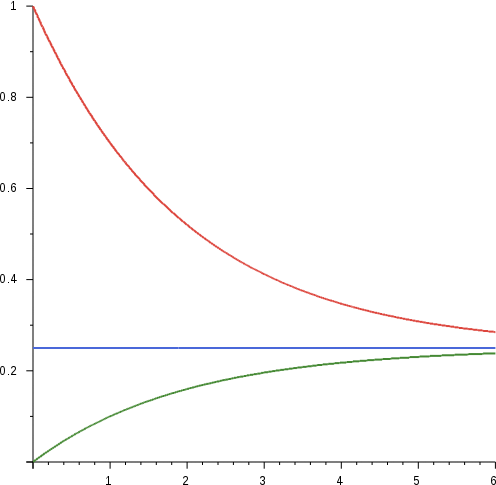
La esencia del modelo Jukes Cantor es retroceder t, la cantidad de tiempo transcurrido desde la fracción de bases alteradas. Conceptualmente, esto es solo invertir los ejes x e y de la curva verde. Para modelar esto cuantitativamente, consideramos la siguiente matriz S (t) que denota las respectivas probabilidades P (x|y, t) de observar la base x dada un estado inicial de base y en el tiempo\(\Delta\) t.
\ [S (\ Delta t) =\ izquierda (\ begin {array} {cccc}
P (A\ media A,\ Delta t) & P (A\ media G,\ Delta t) &\ cdots & P (A\ media T,\ Delta t)\\
P (G\ media A,\ Delta t) &\ cdots &\ cdots\\ cdots\
\ cdots & &\ cdots\\
P (T\ mediados de A,\ Delta t) & \ cdots &\ cdots & P (T\ mid T\ Delta T)
\ end {array}\ derecha)\ nonumber\]
Podemos suponer que se trata de un modelo de markov estacionario, lo que implica que esta matriz es multiplicativa, i.e.
\[S\left(t_{1}+t_{2}\right)=S\left(t_{1}\right) S\left(t_{2}\right)\]
Por muy poco tiempo\(\epsilon\), podemos suponer que no hay efecto de segundo orden, es decir, no hay tiempo suficiente para que ocurran dos mutaciones en el mismo nucleótido. Entonces las probabilidades de las transiciones cruzadas son todas proporcionales a\(\epsilon\). Además, en el modelo Jukes Cantor, asumimos que todas las tasas de transición son las mismas de cada nucleótido a otro nucleótido. Por lo tanto, por un corto tiempo\(\epsilon\)
\ [S (\ épsilon) =\ left (\ begin {array} {cccc}
1-3\ alpha\ epsilon &\ alpha\ epsilon &\ alpha\ epsilon &\ alpha\ epsilon\
\ alpha\ épsilon & 1-3\ alpha\ epsilon &\ alpha\ epsilon &\ alpha\ epsilon &
\ alpha\ epsilon &\ alpha\ epsilon en & 1-3\ alfa\ épsilon &\ alfa\ épsilon\
\ alfa\ épsilon &\ alpha\ épsilon &\ alpha\ épsilon & 1-3\ alpha\ épsilon
\ end {array}\ derecha)\ nonumber\]
En el tiempo t, la matriz viene dada por
\ [S (t) =\ left (\ begin {array} {cccc}
r (t) & s (t) & s (t) & s (t)\\
s (t) & r (t) & s (t) & s (t)\\
s (t) & s (t) & r (t) & s (t)\ s (t) &
s (t) & s (t) & s (t) & r (t)
\ end {array}\ derecha)\ nonumber\]
De la ecuación\(S(t+\epsilon)=S(t) S(\epsilon)\) obtenemos
\[r(t+\epsilon)=r(t)(1-3 \alpha \epsilon)+3 \alpha \epsilon s(t) \text { and } s(t+\epsilon)=s(t)(1-\alpha \epsilon)+\alpha \epsilon r(t))\nonumber\]
Que se reordenan como el sistema acoplado de ecuaciones diferenciales
\[r^{\prime}(t)=3 \alpha(-r(t)+s(t)) \text { and } s^{\prime}(t)=\alpha(r(t)-s(t))\nonumber\]
Con las condiciones iniciales r (0) = 1 y s (0) = 0. Las soluciones se pueden obtener como
\[r(t)=\frac{1}{4}\left(1+3 e^{-4 \alpha t}\right) \text { and } s(t)=\frac{1}{4}\left(1-e^{-4 \alpha t}\right)\nonumber\]
Ahora bien, en una alineación dada, si tenemos la fracción f de los sitios donde difieren las bases, tenemos:
\[f=3 s(t)=\frac{3}{4}\left(1-e^{-4 \alpha t}\right)\nonumber\]
lo que implica
\[t \propto-\log \left(1-\frac{4 f}{3}\right)\nonumber\]
Para acordar asintóticamente con f, establecemos la distancia evolutiva d para ser
\[d=-\frac{3}{4} \log \left(1-\frac{4 f}{3}\right)\nonumber\]
Tenga en cuenta que la distancia es aproximadamente proporcional a f para valores pequeños de f y asintóticamente se acerca al infinito cuando f! 0.75. Intuitivamente esto sucede porque después de un periodo de tiempo muy largo, esperaríamos que la secuencia fuera completamente aleatoria y eso implicaría alrededor de tres cuartas partes de las bases que no coinciden con las originales. Pero los valores de incertidumbre de la distancia Jukes-Cantor también se vuelven muy grandes cuando f se acerca a 0.75.
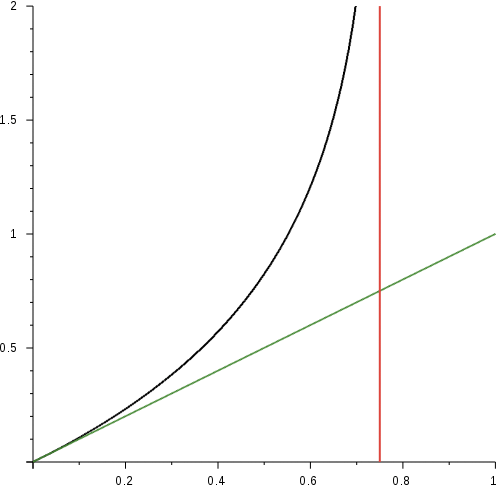
Línea negra denota la curva, verde es la línea de tendencia para valores pequeños de f mientras que la línea roja denota el límite asintótico.
Otros modelos
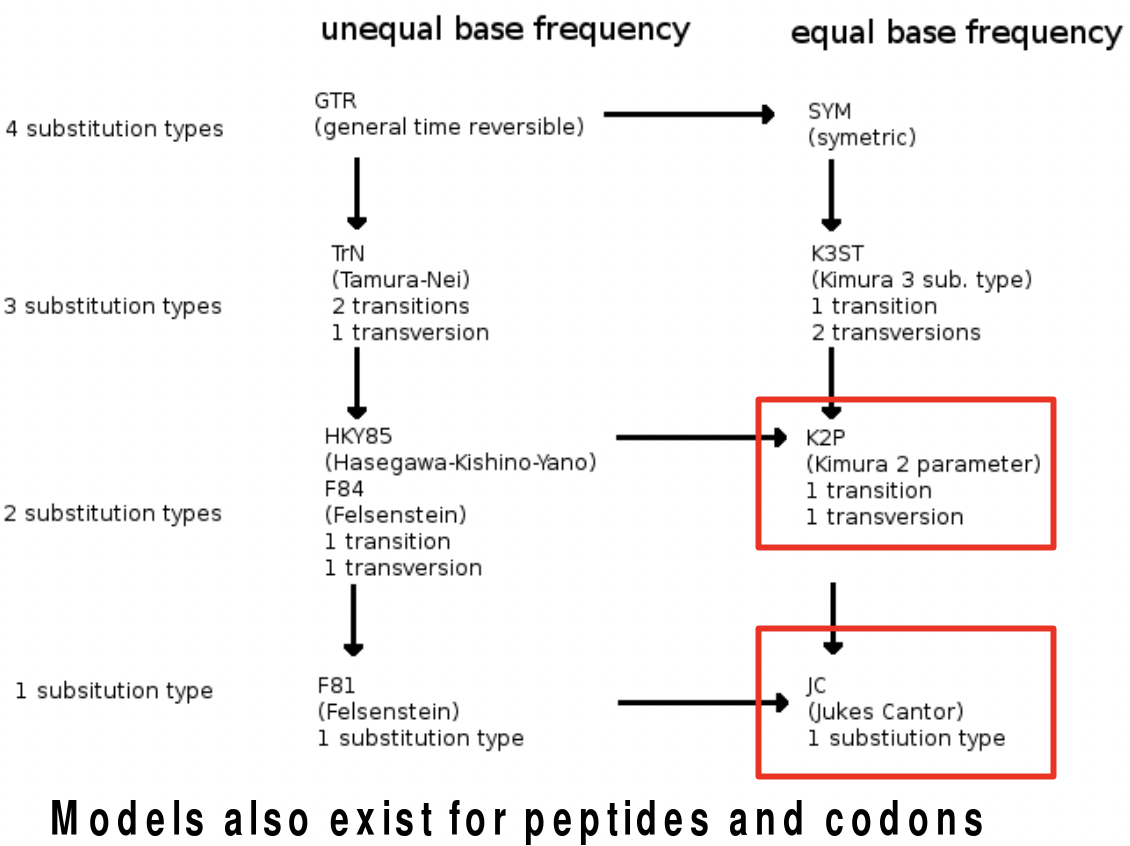
El modelo Jukes Cantor es el modelo más simple que nos da un modelo de distancia aditiva teóricamente consistente. Sin embargo, es un modelo de un parámetro que asume que las mutaciones de cada base a una base diferente tienen la misma probabilidad. Pero, los cambios entre AG o entre TC son más probables que los cambios a través de ellos. El primer tipo de sustitución se llama transiciones mientras que el segundo tipo se llama transversiones. El modelo Kimura tiene dos parámetros que tienen esto en cuenta. También hay muchas otras modificaciones de este modelo de distancia que toma en cuenta las diferentes tasas de transiciones y transversiones etc. que se representan a continuación.
FAQ
P: ¿Podemos usar diferentes parámetros para diferentes partes del árbol? ¿Para dar cuenta de diferentes tasas de mutación?
R: Es posible, es un área de investigación actual.
Distancias a los árboles
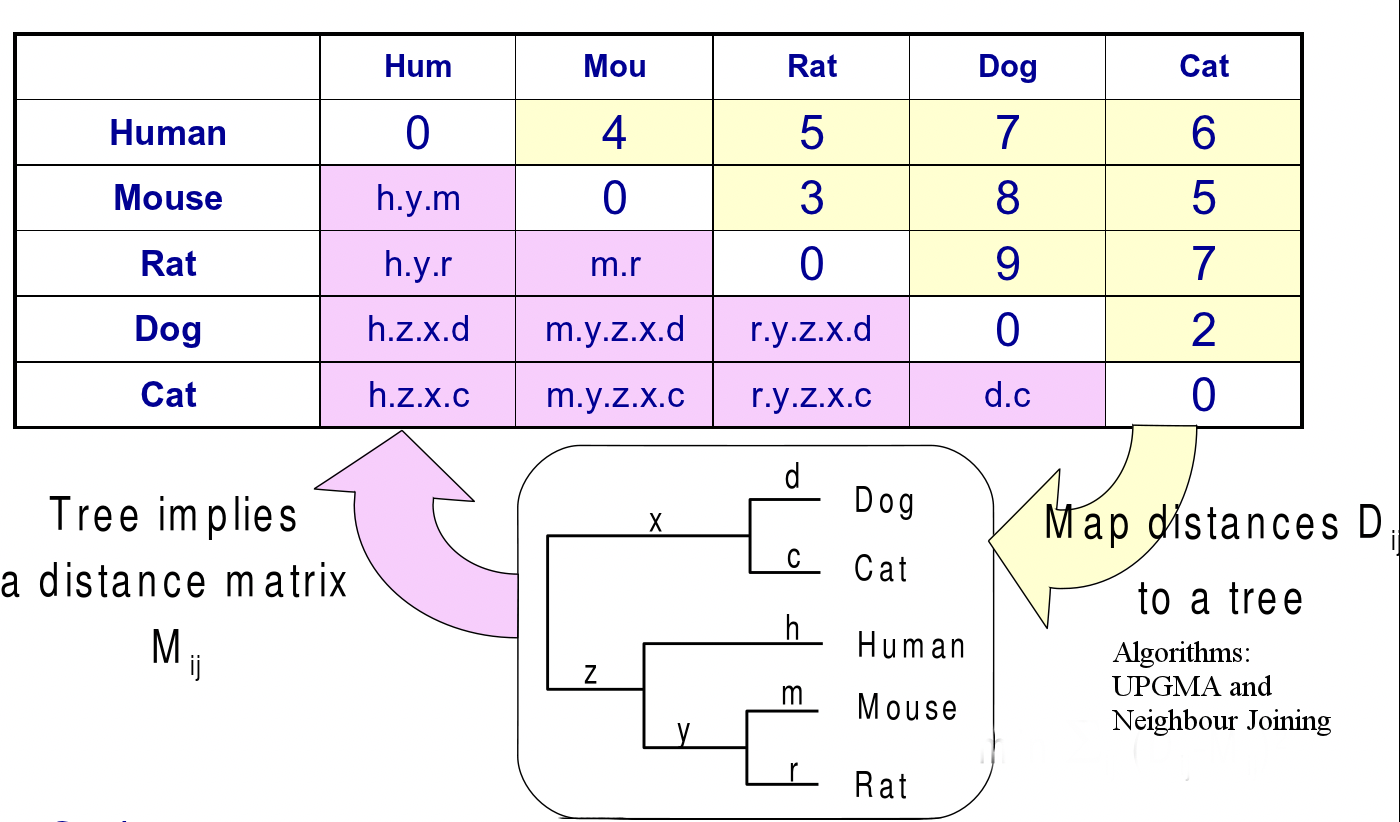
Si tenemos un árbol filogenético ponderado, podemos encontrar el peso total (longitud) del camino más corto entre un par de hojas sumando las longitudes de rama individuales en el camino. Teniendo en cuenta todos esos pares de hojas, tenemos una matriz de distancia que representa los datos. En los métodos basados en distancia, el problema es reconstruir el árbol dada esta matriz de distancia.
Licencia Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use/.
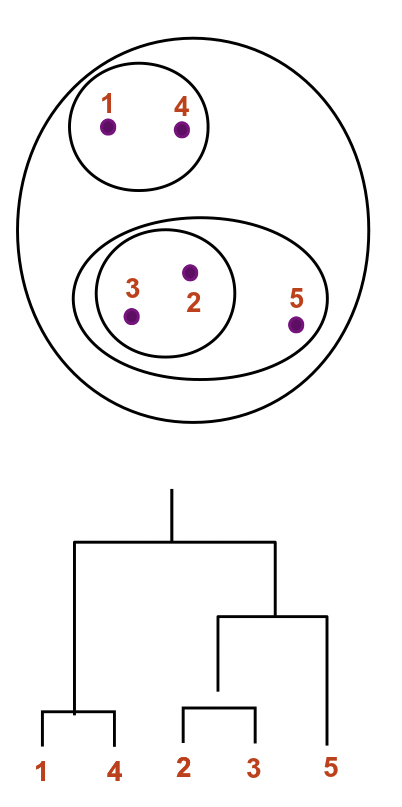
Figura 26.9: Mapeo de un árbol a una matriz de distancia y viceversa
FAQ
P: En la Figura 27.9 Las métricas de divergencia de secuencia m y r pueden tener algún solapamiento por lo que la distancia entre ratón y rata no es simplemente m+r. ¿No sería ese solo el caso si no hubiera superposición?
R: Si modelas la evolución correctamente, entonces obtendrías distancia evolutiva. Es una desigualdad más que una igualdad y coincidimos en que no se puede inferir exactamente que la distancia dada es la distancia precisa. Por lo tanto, la distancia de secuencias entre ratón y rata es probablemente menor que m + r debido a la superposición, evolución convergente y transversiones.
Sin embargo, tenga en cuenta que no existe una correspondencia uno a uno entre una matriz de distancia y un árbol ponderado. Cada árbol sí corresponde a una matriz de distancia, pero lo contrario no siempre es cierto. Una matriz de distancia tiene que satisfacer propiedades adicionales para corresponder a algún árbol ponderado. De hecho, hay dos modelos que asumen restricciones especiales en la matriz de distancia:
Ultramétrico: Para todos los trillizos (a, b, c) de hojas, dos pares entre ellos tienen la misma distancia, y la tercera distancia es menor; es decir, el triplete puede etiquetarse i, j, k de tal manera que
\[d_{i j} \leq d_{i k}=d_{j k}\nonumber\]
Conceptualmente esto se debe a que las dos hojas que están más estrechamente relacionadas (digamos i, j) han divergido de la thrid (k) exactamente al mismo tiempo. y la separación temporal de la tercera debería ser igual, mientras que la separación entre ellas debería ser menor.
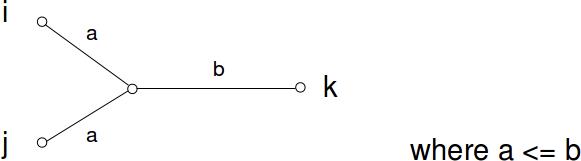
Aditivo: Las matrices aditivas de distancia satisfacen la propiedad de que todos los cuarteto de hojas pueden etiquetarse i, j, k, l de tal manera que
\[d_{i j}+d_{k l} \leq d_{i k}+d_{j l}=d_{i l}+d_{j k}\nonumber\]
De hecho, esto es cierto para todos los árboles de peso positivo. Para cualquier 4 hojas en un árbol, puede haber exactamente una topología, i.e.
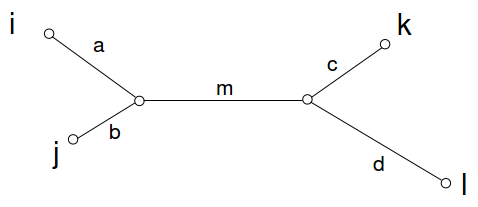
Entonces la condición anterior es término por término equivalente a
\[(a+b)+(c+d) \leq(a+m+c)+(b+m+d)=(a+m+d)+(b+m+c)\nonumber\].
Esta igualdad corresponde a todas las distancias por pares que son posibles de atravesar este árbol.
Estos tipos de ecualidades redundantes deben ocurrir al mapear un árbol a una matriz de distancias, ya que un árbol de n nodos tiene n 1 parámetros, uno para cada longitud de rama, mientras que una matriz de distancia tiene n2 parámetros. Por lo tanto, un árbol es esencialmente una proyección de menor dimensión de un espacio dimensional superior. Un corolario de esta observación es que no todas las matrices de distancia tienen un árbol correspondiente, sino que todos los árboles se mapean a matrices de distancia únicas.
Sin embargo, los conjuntos de datos reales no satisfacen exactamente las restricciones ultraméricas o aditivas. Esto puede deberse al ruido (cuando nuestros parámetros para nuestros modelos evolutivos no son precisos), estocástico y aleatoriedad (debido a pequeñas muestras), fluctuaciones, diferentes tasas de mutaciones, conversiones de genes y transferencia horizontal. Debido a esto, necesitamos algoritmos de construcción de árboles que sean capaces de manejar matrices de distancia ruidosas.
A continuación, se discutirán dos algoritmos que se basan directamente en estos supuestos para la reconstrucción de árboles.
UPGMA - Método de grupo de pares no ponderados con media aritmética
Esto es exactamente lo mismo que el método de agrupamiento jerárquico discutido en la Conferencia 13, Clustering de expresión génica. Forma clústeres paso a paso, desde nodos estrechamente relacionados hasta aquellos que están más separados. Se forma un nodo de ramificación para cada nivel sucesivo. El algoritmo se puede describir correctamente mediante los siguientes pasos:
Inicialización:
1. Definir una hoja i por secuencia x i.
2. Coloca cada hoja i a la altura 0.
3. Definir Clusters C i cada uno teniendo una hoja i.
Iteración:
- Encuentre las distancias por pares d ij entre cada par de clústeres C i, Cj tomando la media aritmética de las distancias entre sus secuencias miembro.
- Encuentra dos cúmulos C i, C j de tal manera que d ij se minimicen.
- Dejar C k =\(C_{i} \cup C_{j}\).
- Definir el nodo k como padre de los nodos i, j y
colocarlo a la altura d ij /2 por encima de i, j.
- Eliminar C i, C j.
Terminación: Cuando quedan dos clústeres C i, Cj, coloca la raíz a la altura d ij /2 como padre de los nodos i, j
Ultrametrificación de árboles no ultramétricos
Si un árbol no satisface condiciones ultramétricas, podemos intentar encontrar un conjunto de alteraciones en una matriz de distancias simétricas nxn que lo hagan ultramétrico. Esto se puede lograr construyendo una gráfica completamente conectada con pesos dados por la matriz de distancia original, encontrando un árbol de expansión mínimo (MST) de esta gráfica, y luego construyendo una nueva matriz de distancia con los elementos D (i, j) dados por el mayor peso en la ruta única en el MST de i a j. el árbol de expansión del gráfico completamente conectado simplemente identifica un subconjunto de bordes que conecta todos los nodos sin crear ningún ciclo, y un árbol de expansión mínimo es un árbol de expansión que minimiza la suma total de pesos de borde. Un MST se puede encontrar usando el algoritmo ie Prims, y luego se usa para corregir un árbol no ultramétrico.
Debilidades de la UPGMA
Si bien este método está garantizado para encontrar el árbol correcto si la matriz de distancia obedece a la propiedad ultramérica, resulta ser un algoritmo inexacto en la práctica. Aparte de la falta de robustez, sufre de la suposición del reloj molecular de que la tasa de mutación a lo largo del tiempo es constante para todas las especies. Sin embargo, esto no es cierto ya que ciertas especies como las ratas y los ratones evolucionan mucho más rápido que otras. Tales diferencias en la tasa de mutación pueden conducir a una atracción de ramas largas; los nodos que comparten una tasa de mutación más baja pero que se encuentran en linajes distintos pueden fusionarse, dejando que aquellos nodos con tasas de mutación más altas (ramas largas) aparezcan juntos en el árbol. La siguiente figura ilustra un ejemplo donde UPGMA falla:
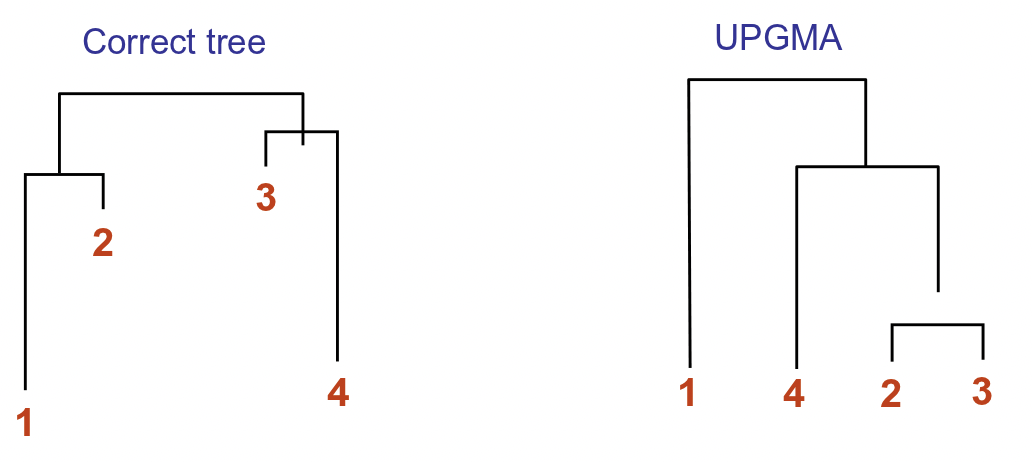
Vecino Uniéndose
Se garantiza que el método de unión de vecinos produzca el árbol correcto si la matriz de distancia satisface la propiedad aditiva. También puede producir un buen árbol cuando hay algo de ruido en los datos. El algoritmo se describe a continuación:
Encontrar las hojas vecinas: Vamos
\[D_{i j}=d_{i j}-\left(r_{i}+r_{j}\right) \text { where } r_{a}=\frac{1}{n-2} \sum_{k} d_{a k}, a \in\{i, j\}\nonumber\]
Aquí n es el número de nodos en el árbol; por lo tanto, ri es la distancia promedio de un nodo a los otros nodos. Se puede probar que la modificación anterior asegura que D ij es mínimo solo si i, j son vecinos. (Una prueba se puede encontrar en la página 189 del libro de Durbin).
Inicialización: Definir T como el conjunto de nodos hoja, uno por secuencia. Dejar L = T
Iteración:
1. Pick i, j tal que D ij se minimice.
2. Definir un nuevo nodo k, y establecer\[d_{k m}=\frac{1}{2}\left(d_{i m}+d_{j m} d_{i j}\right) \forall m \in L\nonumber\]
3. Añadir k a T, con bordes de longitudes\[d_{i k}=\frac{1}{2}\left(d_{i j}+r_{i} r_{j}\right)\nonumber\]
4. Quitar i, j de L
5. Agregar k a L
Terminación: Cuando L consta de dos nodos i, j, y el borde entre ellos de longitud d ij, agregue el nodo raíz como padre de i y j.
Resumen de Métodos a Distancia Pros y Contras
Se ha demostrado que los métodos descritos anteriormente capturan muchas características interesantes de las relaciones filogenéticas, y suelen ser muy rápidos en el sentido algorítmico. Sin embargo, cierta información ciertamente se pierde en la matriz de distancia, y típicamente solo se propone un solo árbol. Se pueden cometer errores graves, como la atracción de ramas largas, cuando se violan los supuestos básicos sobre la tasa de mutación, etc. Por último, los métodos a distancia no hacen inferencia sobre la historia de un sitio en particular, y por lo tanto no hacen sugerencias sobre el estado ancestral de una secuencia.

