27.7: Modelización de Frecuencias de Poblaciones y Alelos
- Page ID
- 54431
Con el advenimiento de la secuenciación de próxima generación, se está volviendo económico secuenciar los genomas de muchos individuos dentro de una población. Para dar sentido a cómo los alelos se propagan a través de una población, es útil contar con un modelo con el que comparar los datos. El modelo de reproducción Wright-Fisher ha ocupado este papel durante los últimos 70 años.
El modelo Wright-Fisher
Al igual que los HMM, Wright-Fisher es un proceso de Markov: en cada paso, el sistema progresa aleatoriamente, y el estado actual del sistema depende únicamente del estado anterior. En este caso, las transiciones de estado representan la reproducción. Al modelar la transmisión de cromosomas a la descendencia, podemos estudiar la deriva genética.
El modelo hace una serie de suposiciones simplificadoras:
1. El tamaño de la población, N, es constante en cada generación.
2. Sólo los miembros de la misma generación se reproducen (sin solapamiento).
3. La reproducción ocurre al azar.
4. El gen que se está modelando solo tiene 2 alelos.
5. Los genes se someten a selección neutra.
Tenga en cuenta que Wright-Fisher no es una opción apropiada si está tratando de modelar el cambio en la frecuencia de un gen para el que se selecciona positiva o negativamente. Si utilizamos Wright-Fisher para modelar los cromosomas de individuos diploides, el tamaño de la población del modelo se convierte en 2N.
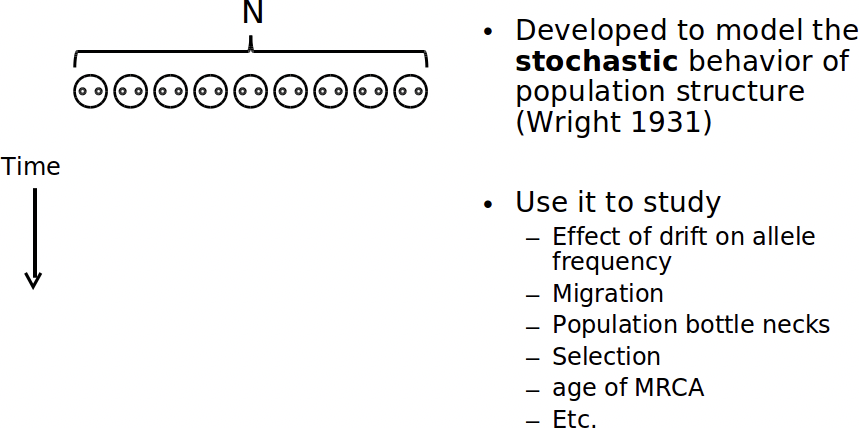
En inglés, así es como funciona Wright-Fisher:
En cada generación, para cada niño, seleccionamos aleatoriamente de los padres (con reemplazo). El alelo del niño se convierte en el del padre seleccionado aleatoriamente.
Repetimos este proceso para muchas generaciones, con los niños sirviendo como los nuevos padres, ignorando el orden de los cromosomas.
Realmente es así de simple. Para determinar la probabilidad de k copias de un alelo existente en la generación hijo cuando tenía una frecuencia de p en la generación padre, podemos usar esta fórmula:
\ [\ left (\ begin {array} {c}
2 N\\
k
\ end {array}\ derecha) p^ {k} q^ {2 n-K}\]
Aquí, q = (1-p). Es la frecuencia de alelos no p en la generación parental.
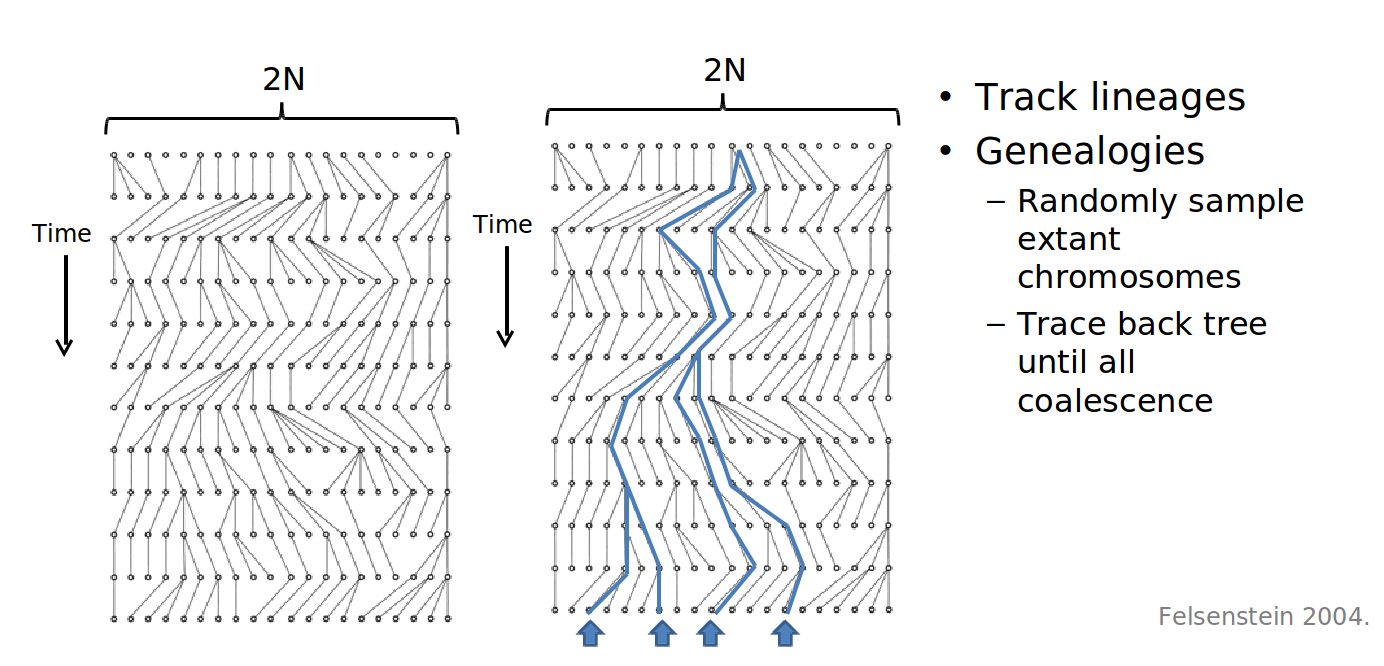
Licencia Commons. Para obtener más información, consulte http://ocw.mit.edu/help/faq-fair-use.
Figura 27.18: Muchas iteraciones de Wright-Fisher produciendo un árbol de linaje
Ahora podemos comenzar a explorar preguntas como: ¿qué tan probable es y cuántas generaciones se espera que tome para que un alelo dado se fije, es decir, el alelo está presente en cada miembro de la población?
El tiempo esperado (en generaciones) para la fijación, dados los supuestos hechos por Wright-Fisher, es proporcional a 4N E, donde NE es el tamaño efectivo de la población.
Nuevamente, es importante tener en cuenta las limitaciones de este modelo y preguntar si realmente tiene sentido para el sistema que estás tratando de representar. Considere cómo podría modificar el modelo propuesto para dar cuenta de una selección coeciente que oscila entre -1 (selección letal negativa) y 1 (selección positiva fuerte).
El modelo coalescente
El problema con el modelo Wright-Fisher es que asume que conoces las frecuencias alélicas de la generación ancentral. Al tratar con los genomas de las especies presentes, estas cantidades son desconocidas. El Modelo Coalescente resuelve este acertijo pensando retrospectivamente. Es decir: comenzamos con los alelos de la generación actual, y trabajamos nuestro camino hacia atrás en el tiempo. El Modelo de Coalescencia básico hace las mismas suposiciones que Wright-Fisher. En cada generación, nos preguntamos: cuál es la probabilidad de que los dos alelos idénticos se unan, o compartan un padre, en la generación anterior.
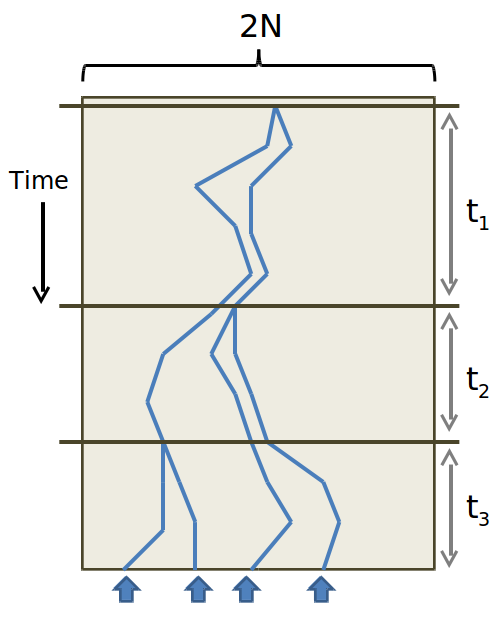
Podemos plantear la probabilidad de que ocurra un evento de coalescencia en la generación anterior como la probabilidad de que la coalescencia no ocurra en ninguna de las generaciones t-1 anteriores a la última, multiplicada por la probabilidad de que ocurra en la generación anterior (la t-ésima) generación. Esto equivale a la expresión:
\[P_{c}(t)=\left(1-\frac{1}{2 N_{e}}\right)^{t-1}\left(\frac{1}{2 N_{e}}\right)\]
Donde N e es el tamaño efectivo de la población.
Al aproximar esta distribución geométrica como exponencial:\(P_{c}(t)=\frac{1}{2 N_{e}} e^{-\left(\frac{t-1}{2 N_{e}}\right)}\), podemos determinar el número esperado de generaciones atrás hasta la coalescencia, que resulta ser 2N e, con una desviación estándar de 2N e.
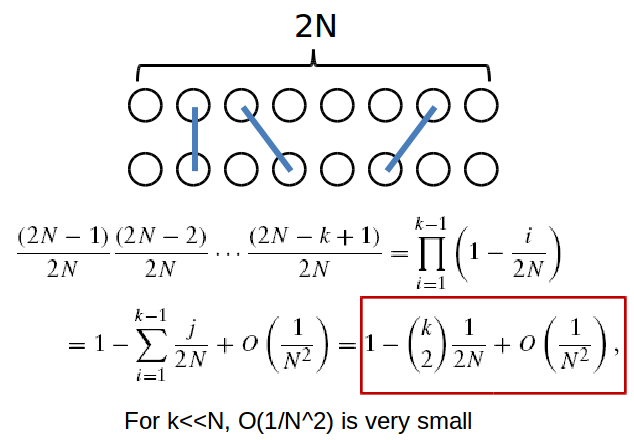
Para preguntar sobre la coalescencia de múltiples linajes en una generación dada, debemos, como en Wright-Fisher, usar una distribución binomial. La probabilidad de que k linajes se coalescen por primera vez en la generación t es:
\ [P\ izquierda (T_ {k} =t\ derecha) =\ izquierda (1-\ izquierda (\ begin {array} {l}
k\\
2
\ end {array}\ derecha)\ frac {1} {2 N}\ derecha) ^ {t-1}\ izquierda (\ begin {array} {l}
k\\
2
\ end {array}\ derecha)\ frac {1} {2 N}\]
Y nuevamente, esto se puede aproximar con una distribución exponencial para k suficientemente grande. El individuo en el que convergen dos linajes se conoce como el Ancestro Común Más Reciente. Al moverse continuamente hacia atrás hasta que todos los antepasados se unen, ¡terminamos con un nuevo tipo de árbol! Y al comparar el árbol resultante de la coalescencia con un árbol genético que hemos construido, las discrepancias entre ambos pueden indicar que se han violado ciertos supuestos del Modelo Coalescente. A saber, la selección puede estar ocurriendo.
El modelo coalescente multiespecie
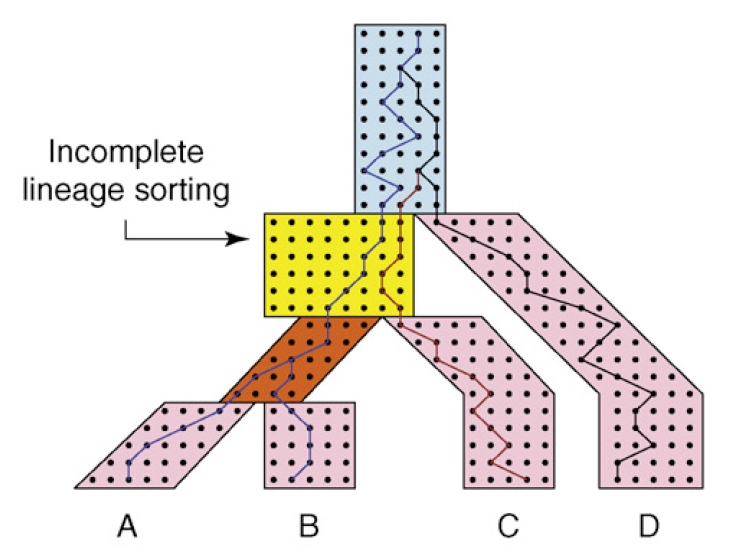
Cortesía de Elsevier, Incorporar. Usado con permiso.
Fuente: Degnan, James H., y Noah A. Rosenberg. “La discordancia del árbol genético, filogenética
Inferencia y el Coalescente Multiespecie”. Tendencias en Ecología y Evolución 24, núm. 6 (2009): 332-40.
Podemos llevar esta idea un paso más allá y rastrear eventos de coalescencia en múltiples especies. Aquí, cada genoma de una especie individual es tratado como linaje.
Tenga en cuenta que existe un tiempo de retraso entre la separación de dos poblaciones y el momento en que dos linajes génicos se unen en un ancestro común. También tenga en cuenta cómo la tasa de coalescencia se ralentiza a medida que N se hace más grande y para ramas cortas.
En la imagen de arriba, la coalescencia profunda se representa en azul claro para tres linajes. Las especies y árboles genéticos aquí son incongruentes ya que C y D son hermanas en el árbol genético pero no en el árbol de la especie.
Existe la\(\frac{2}{3}\) posibilidad de que ocurra incongruencia porque una vez que lleguemos a la sección azul claro, Wright- Fisher no tiene memoria y solo hay\(\frac{1}{3}\) posibilidad de que sea congruente. El efecto de la incongruencia se llama Clasificación de Linaje Incompleto. Al medir la frecuencia con la que ocurre el ILS, obtenemos información sobre poblaciones inusualmente grandes o longitudes de ramas insualmente cortas dentro del árbol de la especie.
Se puede construir un árbol de especies de parsimonia máxima basado en la noción de minimizar el número de eventos de ILS en lugar de minimizar los eventos de duplicación/pérdida implícitos como se cubrió anteriormente. Incluso es posible combinar estos dos métodos para, idealmente, crear una filogenia que sea más precisa de lo que cualquiera de ellos sería individualmente.

