7.2: Un modelo similar al Turing para la Generación de Rayas en Desarrollo de Dígitos (Rivera y Ramírez)
- Page ID
- 53100
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
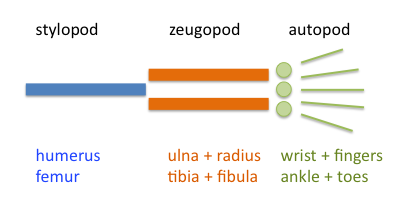
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Tus extremidades primero comienzan a crecer como una pequeña nubbin de tu torso. A medida que las células proliferan, una pequeña varilla de tejido esquelético comienza a crecer justo en el medio. Esto se convertirá en el húmero o fémur. Este tejido esquelético es especificado desde el principio por Sox9, un factor de transcripción que también participa en la determinación del sexo. A medida que el tejido de la extremidad se alarga y se ensancha, aparecen dos huesos paralelos (el radio y el cúbito o la tibia y el peroné). El tejido crece más y más ancho aún, y aparecen cinco huesos paralelos: los metacarpianos y eventualmente las falanges (Figura 3).
 |
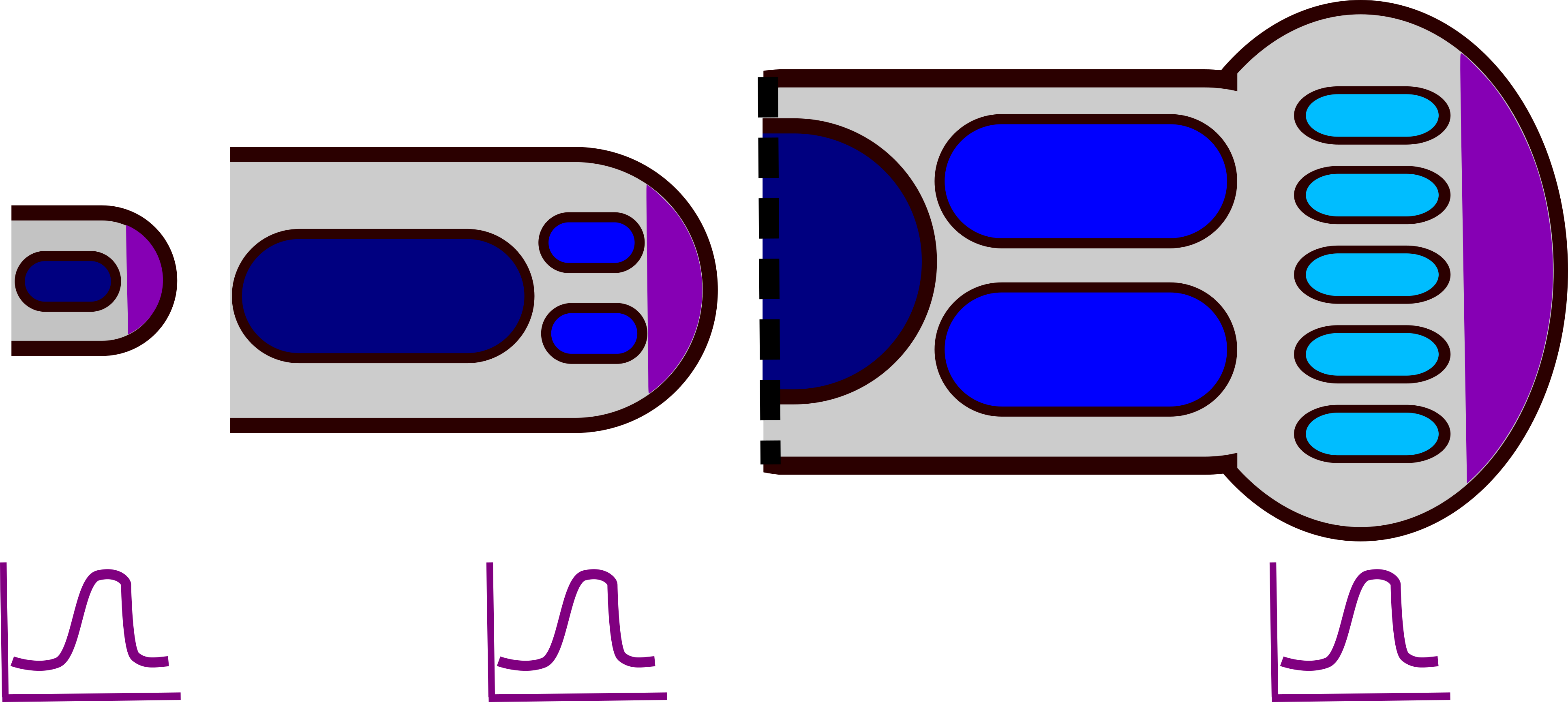 |
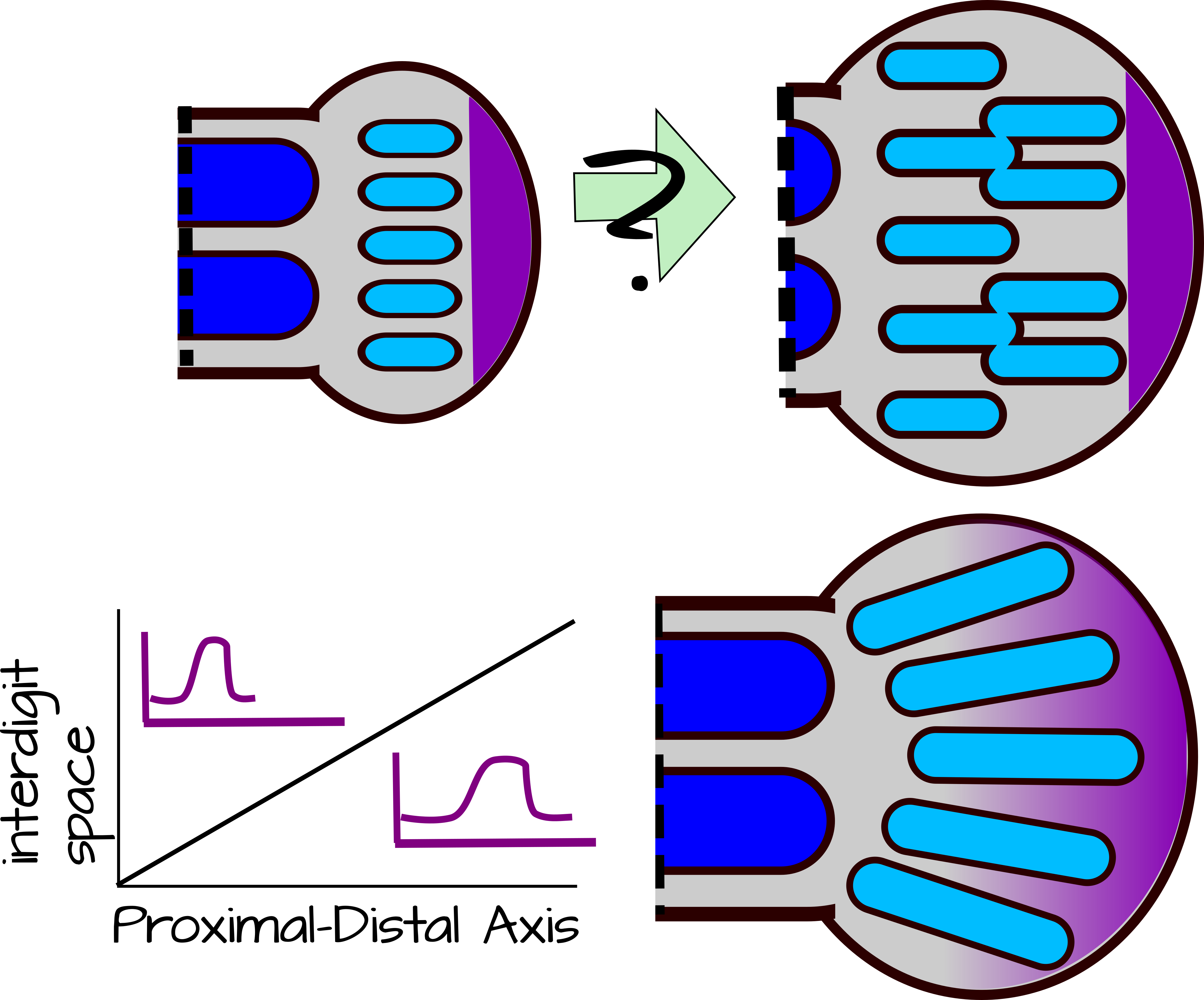
Figura 3: Partes del Extremo Tetrápodo. El panel izquierdo es una imagen de wikimedia commons (Peteruetz) publicada bajo licencia CC BY-SA 3.0. El panel derecho muestra un modelo básico de desarrollo de extremidades tetrápodas. A medida que cada condensación de cartílago (azul, Sox9) se forma, se vuelve represiva a la formación de condensaciones cercanas. La difusión y la fuerza de la represión dan una “longitud de onda” mostrada en púrpura, fuera de la onda, se pueden formar condensaciones (el eje X es el eje proximal-distal y el eje Y es la fuerza de la represión). La región amarilla es una región de inestabilidad (alta concentración de FGF de la cresta ectodérmica apical) donde no se pueden formar condensaciones. A medida que la extremidad crece, hay espacio para más condensaciones con la misma longitud de onda. Un archivo svg editable del panel derecho se puede descargar en https://scholarlycommons.pacific.edu/open-images/32/
Un modelo temprano para el desarrollo de las extremidades propuso que las condensaciones del cartílago producen un morfógeno inhibitorio difusble (que luego se convertirán en huesos de las extremidades). En el brote temprano de la extremidad, este inhibidor puede difundirse a través de todo el pequeño tejido, por lo que solo se deposita una condensación formando el hueso grande del estilópodo. A medida que la extremidad se alarga y se ensancha, el inhibidor no puede alcanzar concentraciones lo suficientemente altas como para cubrir todo el ancho de la yema de la extremidad y se forman dos condensaciones (los huesos paralelos del zeugopodo). En el autópodo en desarrollo, el tejido es lo suficientemente ancho como para soportar 5 condensaciones mutuamente inhibitorias: los cinco dígitos del pie o la mano (Figura 3) 16. Varios modelos de Turing pueden generar un patrón de rayas como este, incluyendo el modelo Activator Inhibidor y el modelo de Sustrate Depletion (Figura 4).
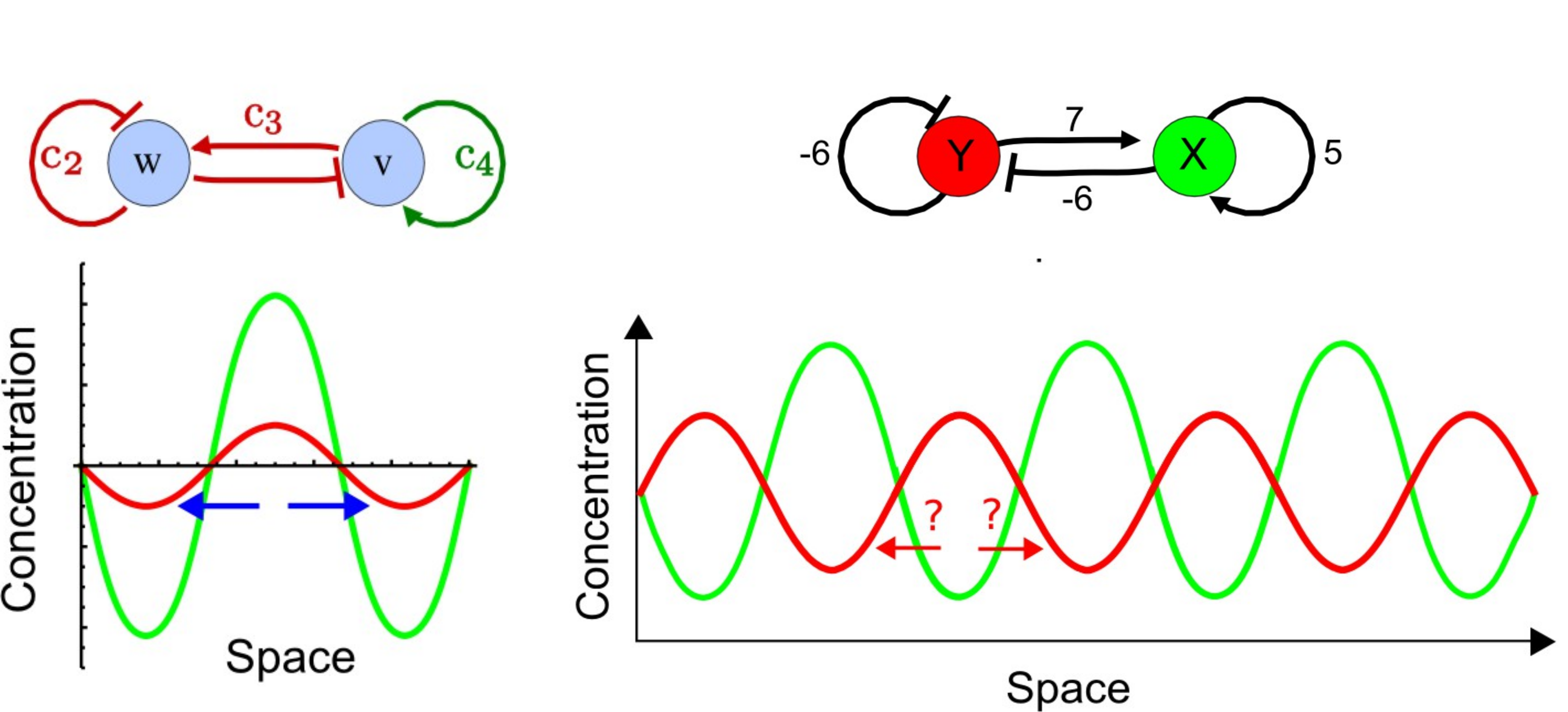 |
Figura 4: Dos modelos Turing para franjas de dígitos. El modelo de la izquierda es un Modelo Activador Inhibidor donde el activador difusible V se activa, así como el inhibidor difusible W. El inhibidor W se inhibe a sí mismo y el activador V. Los cs representan diferentes intensidades de interacción. El modelo de la derecha es un modelo de Agotamiento de Sustrato, donde el activador difusible X utiliza (o inhibe) el sustrato Y. Así el sustrato Y se inhibe a sí mismo activando su propio inhibidor. Para probar entre estos modelos, se puede ensayar la expresión de moléculas que se cree que están involucradas en el proceso. Si los patrones de expresión se superponen (gráfico a la izquierda) entonces se admite el modelo Activator Inhibitor. Si los patrones de expresión son complementarios (gráfico a la derecha) entonces se admite el modelo de Agotamiento de Sustrato. Figura modificada a partir de figuras originales por Marcon et al, 2016 21 publicado originalmente bajo licencia CC BY 4.0 |
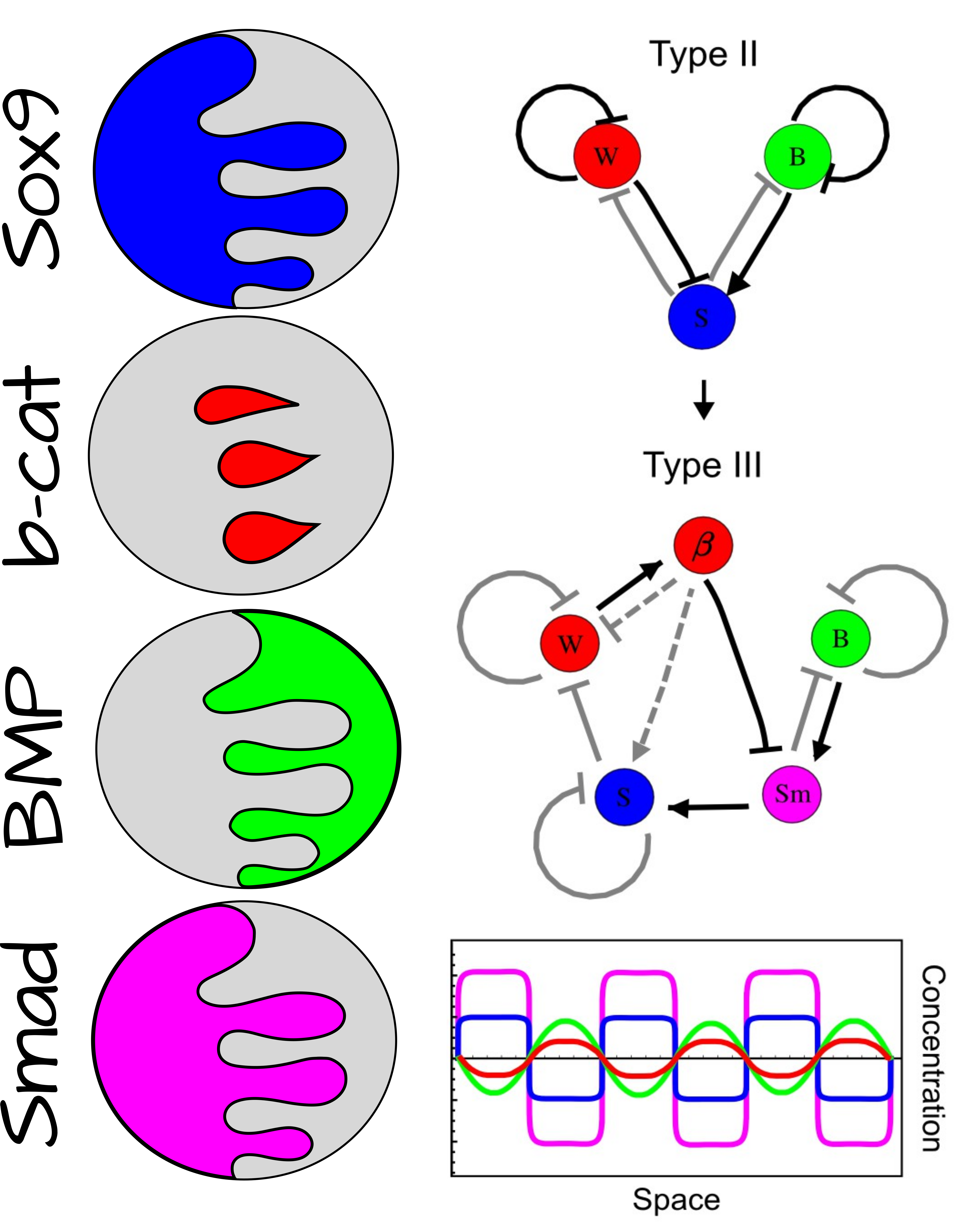
Los experimentos con proteínas expresadas en las áreas interdígito o dígitos proporcionaron soporte para el Modelo de Agotamiento de Sustrato 17. Sin embargo, estos experimentos también mostraron que en lugar de proteínas individuales, el patrón de dígitos en realidad se especifica a través de varias vías de señalización que interactúan. Bmp, Sox9 y Wnt forman los componentes centrales del patrón que genera la “longitud de onda” de la distancia de dígitos. Los tres genes forman gradientes de expresión, con el Sox9 más alto en la mitad de los dígitos y el mayor Bmp y Wnt en los interdígitos (Figura 5) 17. Bmp expresado en las áreas entre dígitos se reprime a sí mismo pero se difunde hacia afuera para activar Sox9 en las celdas cercanas (los dígitos futuros). Sox9 reprime Bmp, asegurando que Bmp solo se exprese en los interdígitos. Los ligandos Wnt son ubicuos, pero sus dianas (incluida la b-catenina) solo se expresan en los interdígitos. La pérdida de b-catenina da como resultado una expansión de la expresión de Sox9 y una expansión de la expresión de b-catenina reduce la expresión de Sox9, lo que sugiere que Wnt/B-catenina es un represor de Sox9 19,20. Estas interacciones dan un modelo donde los dígitos se forman en un patrón regular con una longitud de onda especificada por la fuerza de las interacciones Bmp/Sox9/Wnt y la capacidad de Bmp y Wnt para difundirse (Figura 5) 17.
 |
|
|
Figura 5: El Raspopovic et al. Modelo 17 para especificación de dígitos. Sox9, el marcador de dígito primario, especifica las células para formar condensaciones esqueléticas. Se expresa en las celdas que se convertirán en dígitos en el autópodo. En este modelo, Sox9 (azul) es el activador e interactúa con las vías de señalización BMP y Wnt. Los autopods se muestran como círculos grises en la columna izquierda con patrones de expresión codificados por colores. Sox9 y Smad (púrpura, salida de la ruta BMP) se expresan en los dígitos mientras que BMP (verde) y b-catenina (rojo, salida de la ruta Wnt) se expresan en los interdígitos. La columna izquierda muestra el modelo de Turing para estas interacciones. El modelo superior fue propuesto originalmente por Raspopovic et al 17 y posteriormente refinado por Marcon et al 21. El modelo de Marcon et al mantiene la centralidad de Sox9, que reprime su propia expresión fuera de la condensación. Sox 9 inhibe la vía Wnt, que reprime la b-catenina y otros genes diana en las zonas Sox9. La b-catenina reprime a Smad, que es una diana de señalización BMP difusible. La acción inhibitoria de Smad sobre BMP asegura que BMP no es activa en las células que expresan SMAD, dando a estos dos miembros de la vía BMP patrones de activación complementarios. El panel inferior derecho resume la salida del modelo complejo de Marcon et al. Modificado de Marcon et al 21 originalmente publicado bajo licencia CC BY 4.0 Una versión svg editable de esta figura se puede descargar en: https://scholarlycommons.pacific.edu/open-images/33/ |
Figura 6: Modificación de la longitud de onda. El autópodo en forma de remo debe permitir la formación de condensación adicional a medida que crece. Esto debería conducir a huesos adicionales en la porción distal del autópodo o ramificación de condensaciones existentes (panel superior). Los mutantes de Hoxd13 dan fenotipos como el panel superior, lo que sugiere que Hoxd13 modifica la longitud de onda de las condensaciones Sox9. Hoxd13 se difunde desde la cresta ecodérmica apical y forma un gradiente (amarillo). Donde los niveles de Hoxd13 son altos, la longitud de onda (o espacio entre dígitos) es grande. Donde los niveles de Hoxd13 son bajos, la longitud de onda es pequeña. La modulación de los niveles de Hoxd13 y/o su capacidad para regular la longitud de onda da como resultado dígitos no ramificados 17,18. Una versión svg editable de esta figura se puede descargar en: https://scholarlycommons.pacific.edu/open-images/34/ |
Pero hay un gran problema con esto. A diferencia del zeugopod y el estilópodo, el autópodo tiene forma de remo. Eso significa que crece rápidamente durante el desarrollo, haciendo un tejido que debería soportar más condensaciones de cartílago en la punta que cerca de la muñeca por el modelo propuesto (Figura 6). Este problema lo resuelve Hoxd13. Hoxd13 es un gen Hox que ayuda a modelar las manos, los pies, el tracto no rinario y los órganos reproductivos. En manos y pies (autópodos) se expresa en un gradiente, con los niveles más altos cerca de la cresta ecodérmica apical (AER) en la punta de la yema de la extremidad. Hoxd13 estabiliza el número de dígitos de dos maneras. Primero, actúa como una “zona sin patrones”. En la región con mayor Hoxd13, la expresión de Sox9 es inestable y no se pueden formar nuevas condensaciones. Más lejos de la AER en una zona de bajo Hoxd13, se pueden formar nuevas condensaciones impulsadas por SOX9. Aún más lejos de la AER, donde no hay expresión de Hoxd13, las condensaciones existentes son estables. No se formarán nuevas condensaciones incluso a medida que el tejido se ensancha. Hoxd13 también estabiliza el número de dígitos al aumentar la capacidad de Sox9 para inhibir Bmp y Wnt. Esto tiene el efecto de hacer que la longitud de onda del dígito sea más ancha en la porción distal del autópodo, reprimiendo el desarrollo de dígitos adicionales allí (Figura 6) 18. En mutantes de ratón Hoxd13, las condensaciones de cartílago del autópodo se ramifican en las porciones distales, siguiendo la longitud de onda natural de la interacción Bmp/Sox9/Wnt 18.
 |
Figura 7: Mutaciones en reguladores de la expresión de Sox9. Sox9 se expresa normalmente en elementos esqueléticos vertebrados (futuros huesos y cartílagos). A la izquierda se encuentra el típico patrón de expresión Sox9 en el autópodo. La columna media muestra la expresión normal de tres morfógenos involucrados en el patrón Sox9 en el autópodo. Hox13 (púrpura) proviene de la AER y forma un gradiente que es mayor en el extremo distal e inferior en el extremo proximal. b-cat (beta-catenina, rojo) es el más alto entre los dígitos (en los interdígitos). BMP (verde) es el más alto en todas partes excepto los elementos esqueléticos, incluso en los interdígitos. Las mutaciones de pérdida de función en cada uno de estos genes revelan su función en el ajuste del mecanismo de Turing para la formación de dígitos. Hox13 normalmente establece una longitud de onda Sox9 más larga en el extremo distal de un autópodo. Los mutantes Hox13 exhiben la onda proximal en el extremo distal, lo que resulta en dígitos ramificados. b-cat normalmente evita que Sox9 se exprese en los interdígitos. Los mutantes b-cat exhiben elementos esqueléticos a través del autópodo. BMP normalmente provoca la secreción de Smads, que provocan la expresión de Sox9 en células que no expresan BMP. Los mutantes BMP resultan en una pérdida de elementos esqueléticos. Figura de Desmond Ramírez |
 |
El Dr. Desmond Ramírez, PhD es un Becario Postdoctoral que trabaja en el Laboratorio Katz en UMass, Amherst. Conoce más sobre su trabajo en https://desmondramirez.wordpress.com/ |