8.7: Apéndice - Algoritmo de poda de Felsenstein
- Page ID
- 54271
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El algoritmo de poda de Felsenstein (1973) es un ejemplo de programación dinámica, un tipo de algoritmo que tiene muchas aplicaciones en biología comparada. En la programación dinámica, desglosamos un problema complejo en una serie de pasos más simples que tienen una estructura anidada. Esto nos permite reutilizar los cómputos de manera eficiente y acelera el tiempo requerido para realizar cálculos.
La mejor manera de ilustrar el algoritmo de Felsenstein es a través de un ejemplo, el cual se presenta en los paneles a continuación. Estamos tratando de calcular la probabilidad de un carácter de tres estados en un árbol filogenético que incluye seis especies.
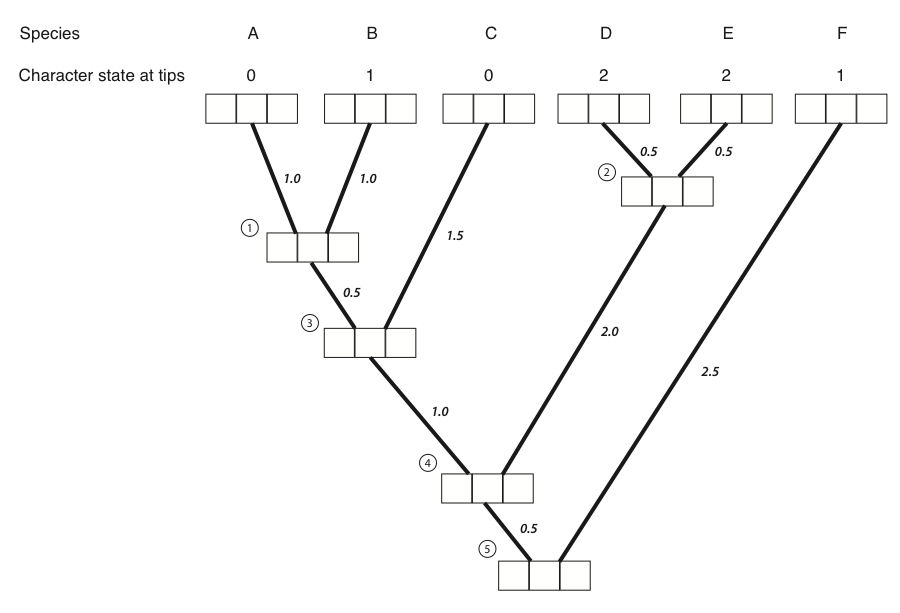
Figura 8.4A. Cada punta y nodo interno en el árbol tiene tres cajas, que contendrán las probabilidades para los tres estados de carácter en ese punto del árbol. La primera caja representa un estado de 0, el segundo estado 1 y el tercer estado 2. Imagen del autor, puede ser reutilizada bajo licencia CC-BY-4.0.
- El primer paso en el algoritmo es llenar las probabilidades para los tips. En este caso, conocemos los estados en las puntas del árbol. Matemáticamente, afirmamos que conocemos con precisión los estados de carácter en las puntas; la probabilidad de que esa especie tenga el estado que observamos es 1, y todos los demás estados tienen probabilidad cero:
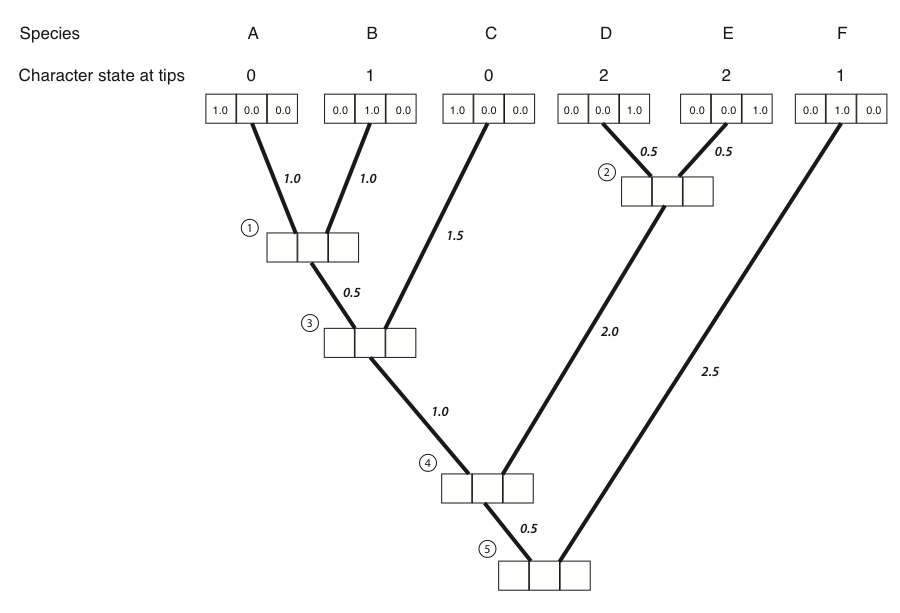
- A continuación, identificamos un nodo donde todos sus descendientes inmediatos son puntas. Siempre habrá al menos uno de esos nodos; muchas veces, habrá más de uno, en cuyo caso elegiremos uno arbitrariamente. Para este ejemplo, elegiremos el nodo que es el ancestro común más reciente de las especies A y B, etiquetado como nodo 1 en la Figura 8.2B.
- Luego usamos la ecuación 7.6 para calcular la probabilidad condicional para cada estado de carácter para el subárbol que incluye el nodo que elegimos en el paso 2 y sus descendientes de punta. Para cada estado de carácter, la probabilidad condicional es la probabilidad, dados los datos y el modelo, de obtener los estados de carácter de punta si comienzas con ese estado de carácter en la raíz. En otras palabras, hacemos un seguimiento de la probabilidad para las partes inclinadas del árbol, incluyendo nuestros datos, si el nodo que estamos considerando tenía cada uno de los posibles estados de carácter. Este cálculo es:
\[ L_P(i) = (\sum\limits_{x \in k}Pr(x|i,t_L)L_L(x)) \cdot (\sum\limits_{x \in k}Pr(x|i,t_R)L_R(x)) \label{8.7}\]
donde i y x son ambos índices para los k estados de caracteres, con sumas tomadas a través de todos los estados posibles en las puntas de rama (x), y términos calculados para cada estado posible en el nodo (i). Las dos partes de la ecuación son el descendiente izquierdo y derecho del nodo de interés. Las ramas pueden asignarse como izquierda o derecha arbitrariamente sin afectar el resultado final, y el enfoque también funciona para las politomías (pero la ecuación es ligeramente diferente). Además, cada una de estas dos piezas en sí tiene dos partes: la probabilidad de comenzar y terminar con cada estado a lo largo de las dos ramas que se consideran, y las probabilidades condicionales actuales que ingresan a la ecuación en las puntas del subárbol (L L (x) y L R (x)). Las longitudes de las ramas se denotan como t L y t R para la izquierda y la derecha, respectivamente.
Se puede pensar en la probabilidad de “fluir” por las ramas del árbol, y las probabilidades condicionales para las ramas izquierda y derecha se combinan a través de la multiplicación en cada nodo, generando la probabilidad condicional para el nodo padre para cada estado de carácter (L P ( i)).
Considere el subárbol que conduce a las especies A y B en el ejemplo dado. Los dos estados de carácter de punta son 0 (para la especie A) y 1 (para la especie B). Podemos calcular la probabilidad condicional para el estado de carácter 0 en el nodo 1 como:
\[ L_P(0) = \left(\sum\limits_{x \in k}Pr(x|0,t_L=1.0)L_L(x)\right) \cdot \left(\sum\limits_{x \in k}Pr(x|0,t_R=1.0)L_R(x)\right) \label{8.8}\]
A continuación, podemos calcular los términos de probabilidad a partir de la matriz de probabilidad P. En este caso t L = t R = 1.0, así tanto para la rama izquierda como para la derecha:
\[ \mathbf{Q}t = \begin{bmatrix} -2 & 1 & 1 \\ 1 & -2 & 1 \\ 1 & 1 & -2 \\ \end{bmatrix} \cdot 1.0 = \begin{bmatrix} -2 & 1 & 1 \\ 1 & -2 & 1 \\ 1 & 1 & -2 \\ \end{bmatrix} \label{8.9}\]
Para que:
\[ \mathbf{P} = e^{Qt} = \begin{bmatrix} 0.37 & 0.32 & 0.32 \\ 0.32 & 0.37 & 0.32 \\ 0.32 & 0.32 & 0.37 \\ \end{bmatrix} \label{8.10}\]
Ahora observe que, dado que se sabe que el estado de carácter izquierdo es cero, L L (0) =1 y L L (1) = L L (2) =0. De igual manera, el estado derecho es uno, por lo que L R (1) =1 y L R (0) = L R (2) =0.
Ahora podemos rellenar las dos partes de la ecuación 8.2:
\[ \sum\limits_{x \in k}Pr(x|0,t_L=1.0)L_L(x) = 0.37 \cdot 1 + 0.32 \cdot 0 + 0.32 \cdot 0 = 0.37 \label{8.11} \]
y:
\[ \sum\limits_{x \in k}Pr(x|0,t_R=1.0)L_R(x) = 0.37 \cdot 0 + 0.32 \cdot 1 + 0.32 \cdot 0 = 0.32 \label{8.11B} \]
Entonces:
L P (0) =0.37 ⋅ 0.32 = 0.12.
Esto significa que bajo el modelo, si el estado en el nodo 1 fuera 0, tendríamos una probabilidad de 0.12 para esta pequeña sección del árbol. Podemos usar un enfoque similar para encontrar que:
(eq. 8.13)
L P (1) =0.32 ⋅ 0.37 = 0.12.
L P (2) =0.32 ⋅ 0.32 = 0.10.
Ahora tenemos la probabilidad para los tres posibles estados ancestrales. Estos números se pueden introducir en las casillas correspondientes:
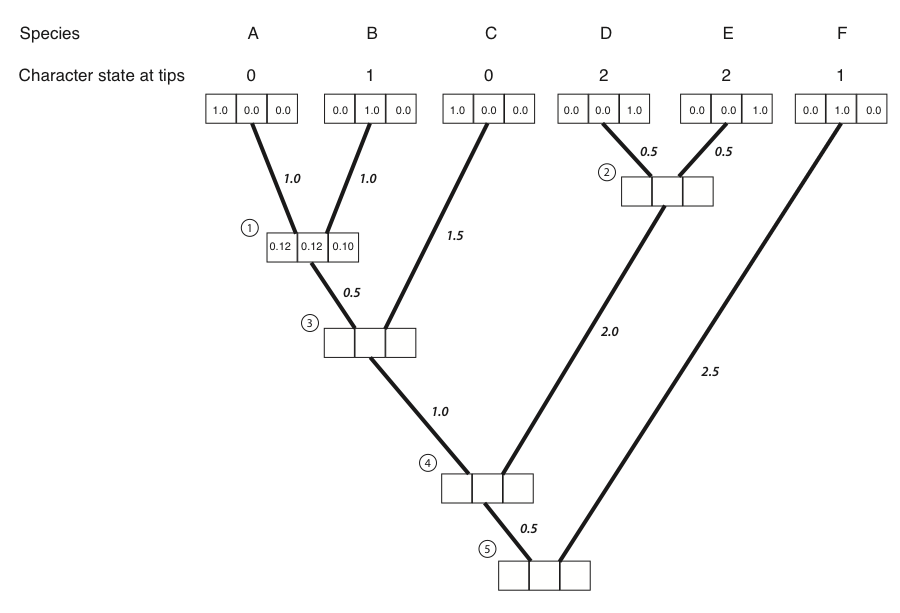
- Luego repetimos el cálculo anterior para cada nodo del árbol. Para los nodos 3-5, no todos los términos L L (x) y L R (x) son cero; sus valores se pueden leer de las cajas del árbol. El resultado de todos estos cálculos:
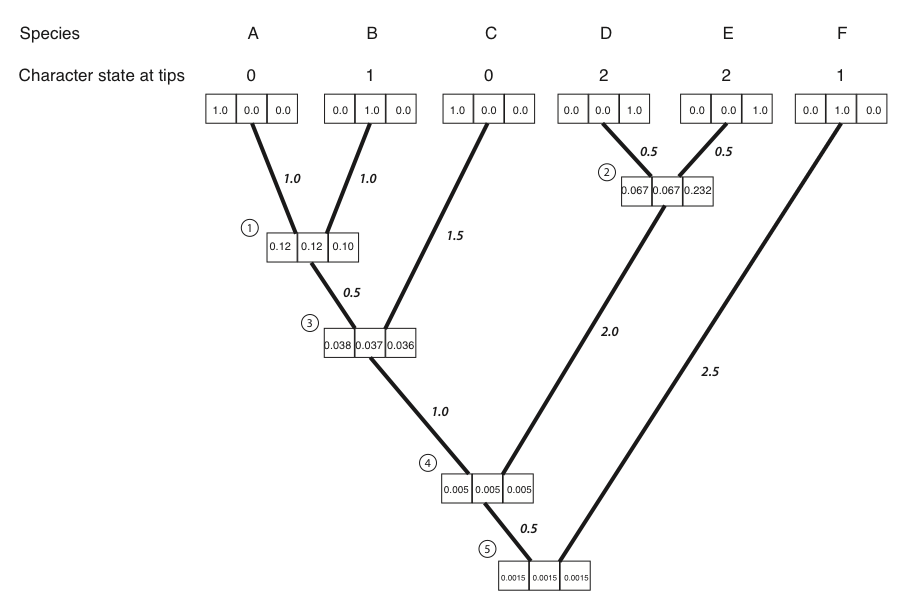
- Ahora podemos calcular la probabilidad en todo el árbol usando las probabilidades condicionales para los tres estados en la raíz del árbol.
\[ L = \sum\limits_{x \in k} \pi_x L_{root} (x) \label{8.14}\]
Donde π x es la probabilidad previa de ese estado de carácter en la raíz del árbol. Para este ejemplo, tomaremos que estas probabilidades previas sean uniformes, iguales para cada estado (π x = 1/ k = 1/3). La probabilidad para nuestro ejemplo, entonces, es:
\[L = 1/3 ⋅ 0.00150 + 1/3 ⋅ 0.00151 + 1/3 ⋅ 0.00150 = 0.00150 \label{8.15}\]
Tenga en cuenta que si prueba este ejemplo en otro paquete de software, como GEIGER o PAUP*, el software calculará una probabilidad de n de -6.5, que es exactamente el log natural del valor calculado aquí.

