11.4: Ajuste de modelos de nacimiento-muerte a tiempos de ramificación

Otro enfoque que utiliza más información en un árbol filogenético consiste en ajustar modelos de nacimiento-muerte a la distribución de los tiempos de ramificación. Este enfoque se remonta a Yule (1925), quien primero aplicó modelos de procesos estocásticos al crecimiento de árboles filogenéticos. Más recientemente, una serie de trabajos de Raup y colegas (Raup et al. 1973; Raup y Gould 1974; Gould et al. 1977; Raup 1985) estimularon enfoques modernos de macroevolución cuantitativa simulando clados aleatorios, demostrando luego cuán variables pueden ser tales clados cultivados bajo modelos simples de nacimiento y muerte ser.

La mayoría de los enfoques modernos para ajustar modelos de nacimiento y muerte a árboles filogenéticos utilizan los intervalos entre eventos de especiación en un árbol, los “tiempos de espera” entre especiaciones sucesivas, para estimar los parámetros de los modelos de nacimiento y muerte. La Figura 10.2 muestra estos tiempos de espera. Con frecuencia, la información sobre el patrón de acumulación de especies en un árbol filogenético se resume mediante una parcela de linaje a través del tiempo (LTT), que es una gráfica del número de linajes en un árbol frente al tiempo (ver Figura 10.9). Como introduje en el Capítulo 10, el eje y de las parcelas LTT se transforma logarítmico, de manera que el patrón esperado bajo un modelo de nacimiento puro de tasa constante es una línea recta. Tenga en cuenta también que las parcelas LTT ignoran el orden relativo de los eventos de especiación. Stadler (2013b) llama a los modelos que justifican tal enfoque “modelos intercambiables de especies”; podemos cambiar la identidad de las especies en cualquier momento sin cambiar el comportamiento esperado del modelo. Debido a esto, los enfoques para entender los modelos de nacimiento-muerte basados en tiempos de ramificación son diferentes y complementarios a los enfoques basados en la topología de árboles, como el equilibrio de árboles.

Como se discutió en el capítulo anterior, aunque muchas veces no tenemos información sobre especies extintas en un clado, todavía podemos (en teoría) inferir la presencia de extinción a partir de una parcela LTT. La señal de extinción es un exceso de linajes jóvenes, lo que se ve como el “tirón de lo reciente” en nuestras parcelas LTT (Figura 10.10). En el siguiente capítulo, demostraré cómo los enfoques estadísticos pueden capturar este patrón de una manera más rigurosa.

Sección 11.4a: Probabilidad de tiempos de espera bajo un modelo de nacimiento-muerte

Para utilizar métodos ML y bayesianos para estimar los parámetros de modelos de nacimiento y muerte a partir de datos comparativos, es necesario anotar las probabilidades de los tiempos de espera entre eventos de especiación en un árbol. Hay un poco de variación en la notación en la literatura, por lo que seguiré Stadler (2013b) y Maddison et al. (2007), entre otros, para mantener la consistencia. Supondremos que el clado comienza en el tiempo t ₁ con un par de especies. La mayoría de los análisis siguen esta convención y condicionan el proceso como que comienza en el momento t ₁, representando el nodo en la raíz del árbol. Esto tiene sentido porque rara vez tenemos información sobre la edad madre de nuestro clado. También condicionaremos que ambos linajes iniciales sobrevivan hasta nuestros días, ya que este es un requisito para obtener un árbol con esta edad de copa (e.g. Stadler 2013a ecuación 5).

Los eventos de especiación y extinción ocurren en varios momentos, y el proceso termina en el tiempo 0 cuando el clado tiene n especies existentes, es decir, medimos el tiempo hacia atrás desde la actualidad. La extinción dará como resultado especies que no se extienden hasta el tiempo 0. Por ahora, asumiremos que solo tenemos datos sobre especies existentes. Nos referiremos al árbol filogenético que muestra tiempos de ramificación que conducen a la especie existente como el árbol reconstruido (Nee et al. 1994). Para un árbol reconstruido con n especies, hay n − 1 tiempos de especiación, que denotaremos como t ₁, t ₂, t ₃,..., t _{n − 1}. Las hojas de nuestro árbol ultramétrico terminan todas en el tiempo 0.

Tenga en cuenta que en esta notación, t ₁ > t ₂ >... > t _{n − 1} > 0, es decir, nuestros tiempos de especiación se miden hacia atrás desde las puntas, y a medida que aumentamos el índice los tiempos van disminuyendo constantemente [esto es un importante diferencia notacional entre Stadler (2013a), usado aquí, y Nee (1994 y otros), este último de los cuales considera los intervalos de tiempo entre eventos de especiación, por ejemplo t ₁ − t ₂ en nuestra notación]. Por ahora, asumiremos un muestreo completo; es decir, todas las n especies vivas en la actualidad están representadas en el árbol.

Ahora derivaremos una probabilidad de observar el conjunto de tiempos de especiación t ₁, t ₂,..., t _{n − 1} dada la diversidad existente del clado, n, y nuestros parámetros del modelo de nacimiento y muerte λ y μ. Para ello, seguiremos muy de cerca un enfoque basado en ecuaciones diferenciales introducidas por Maddison et al. (2007).

La idea general es que asignaremos valores a estas probabilidades en las puntas del árbol, para luego definir un conjunto de reglas para actualizarlas a medida que fluyamos de regreso a través del árbol desde las puntas hasta la raíz. Cuando lleguemos a la raíz del árbol, tendremos la probabilidad de observar el árbol real dado nuestro modelo, es decir, la probabilidad. Este es otro algoritmo de poda.

Para empezar, necesitamos hacer un seguimiento de dos probabilidades: D _N (t), la probabilidad de que un linaje en algún momento t en el pasado evolucione hacia el clado existente N como se observa hoy; y E (t), la probabilidad de que un linaje en algún tiempo t se extinguirá por completo y no dejará descendientes en la actualidad. (Posteriormente, redefiniremos E (t) para que incluya la posibilidad de que los linajes tengan descendientes pero ninguno haya sido muestreado en nuestros datos). Luego aplicamos estas probabilidades al árbol usando tres ideas principales (Figura 11.4)

Figura 11.4. Esquema general de los pasos para calcular la probabilidad de un árbol bajo un modelo de nacimiento-muerte. Imagen inspirada en Maddison et al. (2007) y creada por el autor, puede ser reutilizada bajo una licencia CC-BY-4.0.

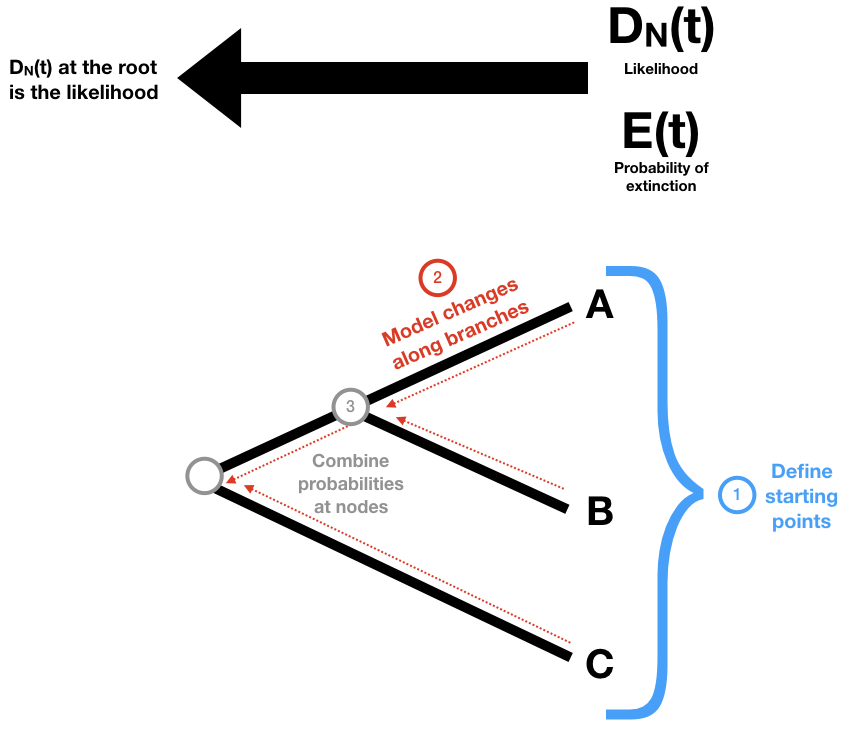
1. Definimos nuestros puntos de partida en las puntas del árbol.

2. Definimos cómo cambian las probabilidades definidas en (1) a medida que avanzamos hacia atrás a lo largo de las ramas del árbol.

3. Definimos lo que sucede con nuestras probabilidades en los nodos del árbol.

Entonces, comenzando por las puntas del árbol, nos dirigimos hacia la raíz. En cada punta, tenemos un valor inicial tanto para D _N (t) como para E (t). Nos movemos hacia atrás a lo largo de las ramas del árbol, actualizando ambas probabilidades a medida que avanzamos usando el paso 2. Cuando dos ramas se unen en un nodo, combinamos esas probabilidades usando el paso 3.

De esta manera, caminamos por el árbol, comenzando por las puntas y pasando por encima de cada rama y nodo (Figura 11.4). Cuando lleguemos a la raíz tendremos D _N (t _{r o o t}), que es toda la probabilidad de que queramos.

Quizás te preguntes por qué necesitamos calcular tanto D _N (t) como E (t) si la probabilidad es capturada por D _N (t) en la raíz. La razón es que la probabilidad de observar un árbol depende de estas probabilidades de extinción calculadas a través del tiempo. Necesitamos hacer un seguimiento de E (t) para saber sobre D _N (t) y cómo cambia. A continuación verá que E (t) aparece directamente en nuestras ecuaciones diferenciales para D _N (t).

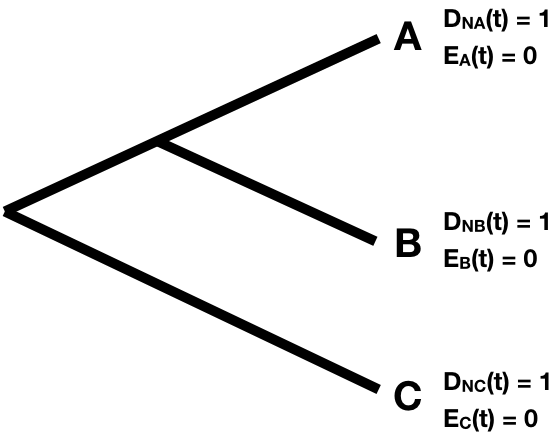
Primero, el punto de partida. Dado que cada tip i representa un linaje vivo, sabemos que está vivo en la actualidad, así podemos definir D _N (t) =1. También sabemos que no se extinguirá antes de ser incluido en el árbol, por lo que E (t) =0. Esto da nuestros valores iniciales para las dos probabilidades en cada punta del árbol (Figura 11.5).

Figura 11.5. Puntos de partida en las puntas de los árboles para los cálculos de probabilidad de Imagen inspirada en Maddison et al. (2007) y creada por el autor, puede ser reutilizada bajo una licencia CC-BY-4.0.

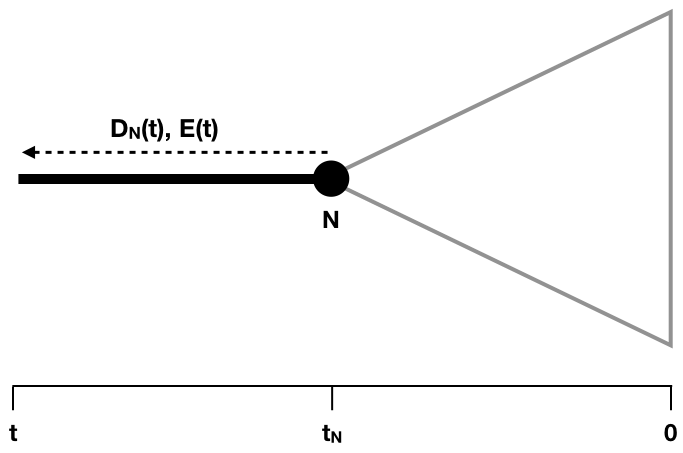
A continuación, imagina que nos movemos hacia atrás por alguna sección de una rama de árbol sin nodos. Consideraremos una rama arbitraria del árbol. Como estamos retrocediendo en el tiempo, comenzaremos en algún nodo del árbol N, que ocurre en un tiempo t _N, y denotaremos el tiempo que vuelve al pasado como t (Figura 11.6).

Figura 11.6. Actualizando D _N (t) y calculando E (t) a lo largo de una rama de árbol. Imagen inspirada en Maddison et al. (2007) y creada por el autor, puede ser reutilizada bajo una licencia CC-BY-4.0.

Como esa sección de rama existe en nuestro árbol, sabemos dos cosas: el linaje no se extinguió durante ese tiempo, y si se producía la especiación, el linaje que se separó no sobrevivió hasta nuestros días. Podemos capturar estas dos posibilidades en una ecuación diferencial que considera cómo cambia nuestra probabilidad general a lo largo de una unidad de tiempo muy pequeña (Maddison et al. 2007).

\[ \frac{dD_N(t)}{dt} = -(\lambda + \mu) D_N(t) + 2 \lambda E(t) D_N(t) \label{11.12} \]

Aquí, la primera parte de la ecuación, − (λ + μ) D _N (t), representa la probabilidad de no especiarse ni extinguirse, mientras que la segunda parte, 2 λ E (t) D _N (t), representa la probabilidad de especiación seguida de la extinción definitiva de uno de los dos linajes hijos. El 2 en esta ecuación aparece porque debemos dar cuenta de que, siguiendo la especiación de un antepasado a las hijas A y B, veríamos el mismo patrón sin importar cuál de los dos descendientes sobrevivió hasta el presente.

También necesitamos calcular nuestra probabilidad de extinción volviendo a través del árbol (Maddison et al. 2007):

\[ \frac{dE(t)}{dt} = \mu - (\mu + \lambda) E(t) + \lambda E(t)^2 \label{11.13} \]

Las tres partes de esta ecuación representan las tres formas en que un linaje podría no llegar a nuestros días: o se extingue durante el intervalo que se considera (μ), sobrevive a ese intervalo pero se extingue algún tiempo después (− (μ + λ) E (t )), o especia en el intervalo pero ambos descendientes se extinguen antes del día de hoy (λ E (t) ²) (Maddison et al. 2007). A diferencia del término D _N (t), esta probabilidad depende únicamente del tiempo y no de la estructura topológica del árbol.

También especificaremos que λ > μ; es posible relajar esa suposición, pero hace que la solución sea más complicada.

Podemos resolver estas ecuaciones para que podamos actualizar la probabilidad moviéndonos hacia atrás a lo largo de cualquier rama del árbol con longitud t. Primero, resolviendo la ecuación 11.13 y usando nuestra condición inicial E (0) = 0:

\[ E(t) = 1 - \frac{\lambda-\mu}{\lambda - (\lambda-\mu)e^{(\lambda - \mu)t}} \label{11.14} \]

Ahora podemos sustituir esta expresión por E (t) en Ecuación\ ref {11.12} y resolver

\[ D_N(t) = e^{-(\lambda - \mu)(t - t_N)} \frac{(\lambda - (\lambda-\mu)e^{(\lambda - \mu)t_N})^2}{(\lambda - (\lambda-\mu)e^{(\lambda - \mu)t})^2} \cdot D_N(t_N) \label{11.15}\]

Recuerde que t _N es la profundidad (medida desde la actualidad) del nodo N (Figura 11.6).

Por último, debemos considerar qué sucede cuando dos ramas se unen en un nodo. Como hay un nodo, sabemos que ha habido un evento de especiación. Multiplicamos los cálculos de probabilidad que fluyen por cada rama por la probabilidad de un evento de especiación [Maddison et al. (2007); Figura 11.7].

Figura 11.7. Actualizando D _N (t) y E (t) a lo largo de una rama de árbol. Imagen inspirada en Maddison et al. (2007) y creada por el autor, puede ser reutilizada bajo una licencia CC-BY-4.0.

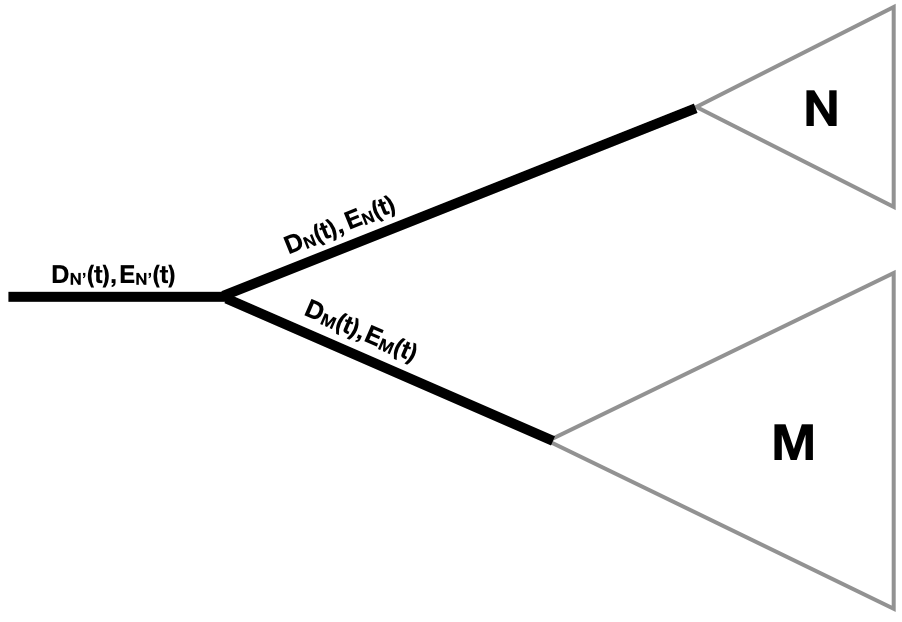
Entonces:

\[D_{N′}(t)=D_N(t)D_M(t)λ \label{11.16}\]

Donde clado N' es el clado conformado por la combinación de dos clados hermanos N y M.

Para aplicar este enfoque en todo un árbol filogenético, multiplicamos las Ecuaciones\ ref {11.15} y\ ref {11.16} en todas las ramas y nodos del árbol. Así, la probabilidad total es (Maddison et al. 2007; Morlon et al. 2011):

\[ L(t_1, t_2, \dots, t_n) = \lambda^{n-1} \big[ \prod_{k = 1}^{2n-2} e^{(\lambda-\mu)(t_{k,b} - t_{k,t})} \cdot \frac{(\lambda - (\lambda-\mu)e^{(\lambda - \mu)t_{k,t}})^2}{(\lambda - (\lambda-\mu)e^{(\lambda - \mu)t_{k,b}})^2} \big] \label{11.17}\]

Aquí, n es el número de puntas en el árbol (tenga en cuenta que la derivación original en Maddison usa n como número de nodos, pero la he cambiado por consistencia con el resto del libro).

El producto en la Ecuación\ ref {11.17} se toma sobre todas las 2 n − 2 ramas del árbol. Cada rama k tiene dos veces asociadas con ella, una hacia la base del árbol, t _{k, b}, y otra hacia las puntas, t _{k, t}.

La mayoría de los métodos que ajustan modelos de nacimiento y muerte a árboles condicionan la existencia de un árbol, es decir, condicionando que todo el proceso no se extinguiera antes del día de hoy, y el evento de especiación del nodo raíz condujo a dos linajes sobrevivientes. Para hacer este condicionamiento, dividimos la Ecuación\ ref {11.17} por λ [1 − E (t _{r o o t})] ² (Morlon et al. 2011; Stadler 2013a).

Adicionalmente, las probabilidades de tiempos de espera de nacimiento-muerte, por ejemplo las de la derivación original de Nee, incluyen un término adicional, (n − 1)!. Esto se debe a que hay (n − 1)! topologías posibles para cualquier conjunto de n − 1 tiempos de espera, todos igualmente probables. Dado que este término es constante para un tamaño de árbol dado n, entonces dejarlo fuera no influye en las probabilidades relativas de diferentes valores de parámetros, pero es necesario conocer este multiplicador si se comparan probabilidades entre diferentes modelos para la selección de modelos, o se compara la salida de diferentes programas (Stadler 2013a).

Teniendo en cuenta estos dos factores, la probabilidad total es:

\[ L(\tau) = (n-1)! \frac{\lambda^{n-2} \big[ \prod_{k = 1}^{2n-2} e^{(\lambda-\mu)(t_{k,b} - t_{k,t})} \cdot \frac{(\lambda - (\lambda-\mu)e^{(\lambda - \mu)t_{k,t}})^2}{(\lambda - (\lambda-\mu)e^{(\lambda - \mu)t_{k,b}})^2} \big]}{ [1-E(t_{root})]^2} \label{11.18}\]

donde:

\[ E(t_{root}) = 1 - \frac{\lambda-\mu}{\lambda - (\lambda-\mu)e^{(\lambda - \mu)t_{root}}}\label{11.19}\]

Sección 11.4b: Usar máxima verosimilitud para ajustarse a un modelo de nacimiento-muerte

Dada la ecuación 11.19 para la probabilidad, podemos estimar las tasas de natalidad y mortalidad utilizando enfoques ML y bayesianos. Para la estimación de ML, maximizamos la ecuación 11.19 sobre λ y μ. Para un modelo de nacimiento puro, podemos establecer μ = 0, y la estimación de máxima verosimilitud de λ se puede calcular analíticamente como:

\[ \lambda= \frac{n-2}{s_{branch}} \label{11.20} \]

donde s _{b r a n c h} es la suma de longitudes de rama en el árbol,

\[ s_{branch} = \sum_{i=1}^{n-1} t_i + t_{n-1} \label{11.21} \]

La ecuación\ ref {11.21} también se llama el estimador Kendal-Moran de la tasa de especiación (Nee 2006).

Para un modelo de nacimiento-muerte, podemos usar métodos numéricos para maximizar la probabilidad sobre λ y μ.

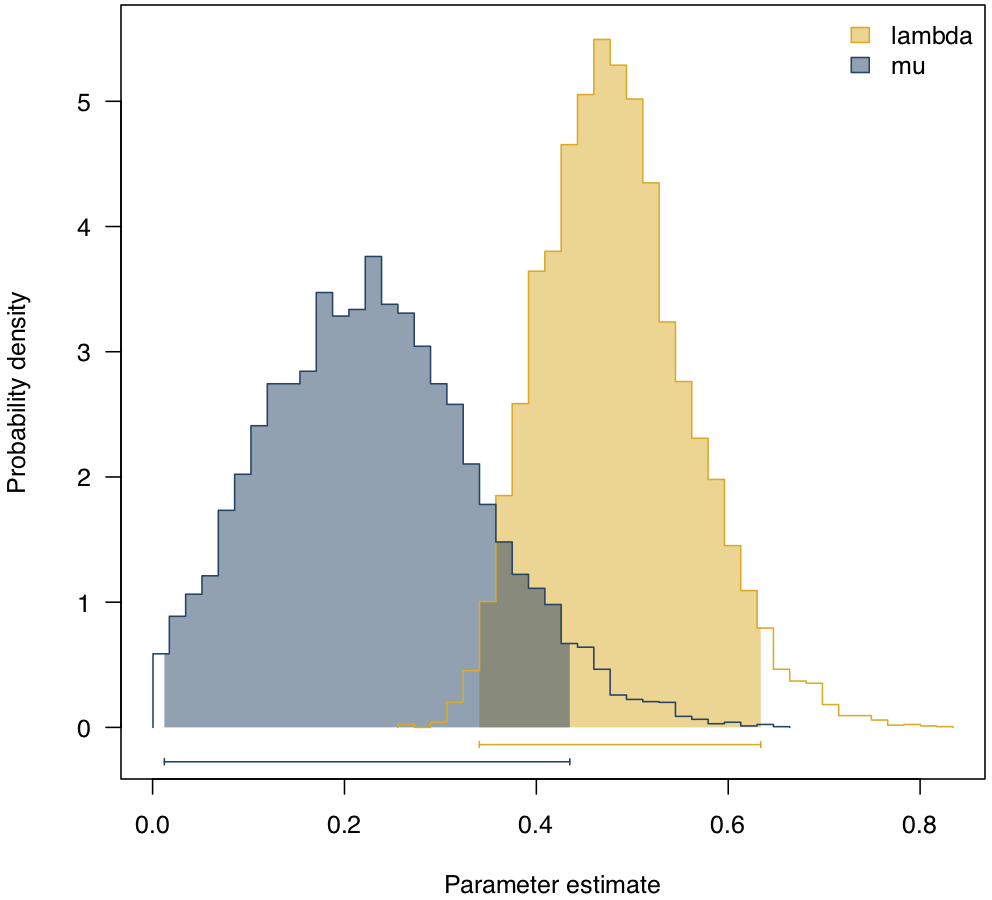
Por ejemplo, podemos usar ML para ajustar un modelo de nacimiento-muerte al árbol Lupinus (Drummond et al. 2012), que tiene 137 especies de puntas y una edad total de 16.6 millones de años. Al hacerlo, obtenemos estimaciones de parámetros ML de λ = 0.46 y μ = 0.20, con una probabilidad logarítmica de l n L _{b d} = 262.3. Compare esto con un modelo de nacimiento puro en el mismo árbol, que da λ = 0.35 y l n L _{p b} = 260.4. Se puede comparar el ajuste de estos dos modelos usando puntuaciones AIC: A I C _{b d} = −520.6 y A I C _{p b} = −518.8, por lo que el modelo de nacimiento y muerte tiene un mejor (menor) puntaje AIC pero por menos de dos unidades AIC. Una prueba de razón de verosimilitud, que da Δ = 3.7 y P = 0.054. En otras palabras, estimamos una tasa de extinción distinta de cero en el clado, pero la evidencia que sustenta ese modelo sobre un modelo de nacimiento puro no es particularmente fuerte. Aunque esta selección de modelo sea un poco ambigua, recuerda que también hemos estimado parámetros utilizando toda la información que tenemos en los tiempos de espera del árbol filogenético.

Sección 11.4c: Uso de MCMC bayesiano para adaptarse a un modelo de nacimiento-muerte

También podemos estimar las tasas de natalidad y mortalidad utilizando un MCMC bayesiano. Podemos usar exactamente el método descrito anteriormente para edades y diversidades de clados, pero sustituir la ecuación\ ref {11.11} por la verosimilitud, utilizando así los tiempos de espera derivados de un árbol filogenético para estimar los parámetros del modelo.

Aplicando esto a los altramuces con los mismos antecedentes que antes, obtenemos las distribuciones posteriores que se muestran en la figura 11.5. La media de la posterior para cada parámetro es λ = 0.48 y μ = 0.23, bastante cercana a las estimaciones de ML para estos parámetros.

Figura 11.8. Distribución posterior para b y d para Lupinus. Datos de (Drummond et al. 2012), imagen inspirada en Maddison et al. (2007) y creada por el autor, puede ser reutilizada bajo una licencia CC-BY-4.0.