25.4: Límites ambientales al crecimiento poblacional
- Page ID
- 58244
Aunque las historias de vida describen la forma en que muchas características de una población (como su estructura de edad) cambian con el tiempo de manera general, los ecologistas poblacionales hacen uso de una variedad de métodos para modelar matemáticamente la dinámica poblacional. Estos modelos más precisos pueden usarse para describir con precisión los cambios que ocurren en una población y predecir mejor los cambios futuros. Ciertos modelos que han sido aceptados durante décadas ahora están siendo modificados o incluso abandonados debido a su falta de capacidad predictiva, y los académicos se esfuerzan por crear nuevos modelos efectivos.
Crecimiento Exponencial
Charles Darwin, en su teoría de la selección natural, fue muy influenciado por el clérigo inglés Thomas Malthus. Malthus publicó un libro en 1798 afirmando que las poblaciones con recursos naturales ilimitados crecen muy rápidamente, y luego el crecimiento poblacional disminuye a medida que los recursos se agotan. Este patrón acelerado de aumento del tamaño de la población se llama crecimiento exponencial.
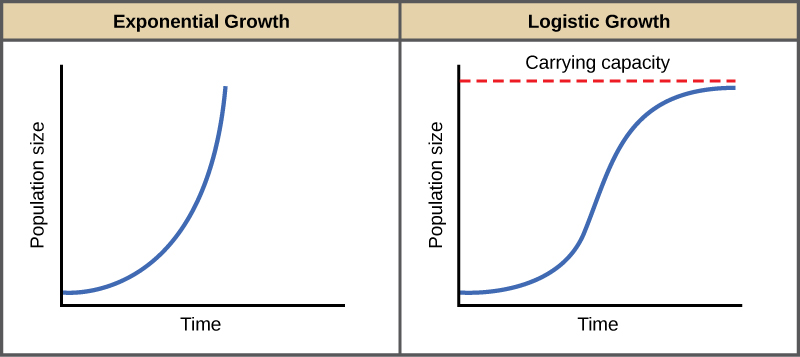
El mejor ejemplo de crecimiento exponencial se observa en bacterias. Las bacterias son procariotas que se reproducen por fisión procariota. Esta división toma alrededor de una hora para muchas especies bacterianas. Si se colocan 1000 bacterias en un matraz grande con un suministro ilimitado de nutrientes (por lo que los nutrientes no se agotarán), después de una hora, hay una ronda de división y cada organismo se divide, resultando en 2000 organismos, un aumento de 1000. En otra hora, cada uno de los 2000 organismos se duplicará, produciendo 4000, un incremento de 2000 organismos. Después de la tercera hora, debería haber 8000 bacterias en el matraz, un aumento de 4000 organismos. El concepto importante de crecimiento exponencial es que la tasa de crecimiento poblacional —el número de organismos añadidos en cada generación reproductiva— se está acelerando; es decir, está aumentando a un ritmo cada vez mayor. Después de 1 día y 24 de estos ciclos, la población habría aumentado de 1000 a más de 16 mil millones. Cuando el tamaño de la población, N, se traza a lo largo del tiempo, se produce una curva de crecimiento en forma de J (Figura\(\PageIndex{1}\)).
El ejemplo de bacterias no es representativo del mundo real donde los recursos son limitados. Además, algunas bacterias morirán durante el experimento y por lo tanto no se reproducirán, disminuyendo la tasa de crecimiento. Por lo tanto, al calcular la tasa de crecimiento de una población, la tasa de mortalidad (D) (número de organismos que mueren durante un intervalo de tiempo determinado) se resta de la tasa de natalidad (B) (número de organismos que nacen durante ese intervalo). Esto se muestra en la siguiente fórmula:
\[\dfrac{\boldsymbol{\Delta N} \text{ (change in number)}} {\boldsymbol{\Delta T} \text{ (change in time)}} = B \text{ (birth rate)} - D \text{ (death rate)} \nonumber\]
La tasa de natalidad generalmente se expresa sobre una base per cápita (para cada individuo). Así, B (tasa de natalidad) = bN (la tasa de natalidad per cápita “b” multiplicada por el número de individuos “N”) y D (tasa de mortalidad) = dN (la tasa de mortalidad per cápita “d” multiplicada por el número de individuos” N”). Adicionalmente, los ecologistas están interesados en la población en un momento determinado, un intervalo de tiempo infinitamente pequeño. Por esta razón, se utiliza la terminología del cálculo diferencial para obtener la tasa de crecimiento “instantánea”, reemplazando el cambio en número y tiempo por una medición instantánea específica de número y tiempo.
\[\dfrac{d N} {d T} = bN - dN = (b - d)N \nonumber\]
Observe que la “d” asociada al primer término se refiere a la derivada (ya que el término se usa en el cálculo) y es diferente de la tasa de mortalidad, también llamada “d”. La diferencia entre las tasas de natalidad y mortalidad se simplifica aún más al sustituir el término “r” (tasa intrínseca de aumento) por la relación entre las tasas de natalidad y mortalidad:
\[\dfrac{d N} {d T} = rN \nonumber\]
El valor “r” puede ser positivo, es decir, la población está aumentando de tamaño; o negativo, es decir, la población está disminuyendo de tamaño; o cero, donde el tamaño de la población es inmutable, condición conocida como crecimiento poblacional cero. Un refinamiento adicional de la fórmula reconoce que diferentes especies tienen diferencias inherentes en su tasa intrínseca de aumento (a menudo pensada como el potencial de reproducción), incluso en condiciones ideales. Obviamente, una bacteria puede reproducirse más rápidamente y tener una mayor tasa intrínseca de crecimiento que un ser humano. La tasa máxima de crecimiento para una especie es su potencial biótico, o r max, cambiando así la ecuación a:
\[\dfrac{d N} {d T} = r_\text{max}N \nonumber\]
Crecimiento Logístico
El crecimiento exponencial sólo es posible cuando se dispone de infinitos recursos naturales; este no es el caso en el mundo real. Charles Darwin reconoció este hecho en su descripción de la “lucha por la existencia”, que establece que los individuos competirán (con miembros de su propia u otra especie) por recursos limitados. Los exitosos sobrevivirán para transmitir sus propias características y rasgos (que ahora sabemos que son transferidos por genes) a la siguiente generación a un ritmo mayor (selección natural). Para modelar la realidad de los recursos limitados, los ecologistas poblacionales desarrollaron el modelo de crecimiento logístico.
Capacidad de carga y modelo logístico
En el mundo real, con sus limitados recursos, el crecimiento exponencial no puede continuar indefinidamente. El crecimiento exponencial puede ocurrir en entornos donde hay pocos individuos y abundantes recursos, pero cuando el número de individuos sea lo suficientemente grande, los recursos se agotarán, desacelerando la tasa de crecimiento. Eventualmente, la tasa de crecimiento se meseta o se nivelará (Figura\(\PageIndex{1}\)). Este tamaño de población, que representa el tamaño máximo de la población que un ambiente en particular puede soportar, se denomina capacidad de carga, o K.
La fórmula que utilizamos para calcular el crecimiento logístico agrega la capacidad de carga como una fuerza moderadora en la tasa de crecimiento. La expresión “K — N” es indicativa de cuántos individuos pueden agregarse a una población en una etapa determinada, y “K — N” dividido por “K” es la fracción de la capacidad de carga disponible para un mayor crecimiento. Así, el modelo de crecimiento exponencial se ve restringido por este factor para generar la ecuación de crecimiento logístico:
\ [\ dfrac {d N} {d T}
= r_\ texto {max}\ dfrac {d N} {d T}
= r_\ texto {max} N\ dfrac {(K-N)} {K}
\ nonumber\]
Observe que cuando N es muy pequeño, (K-N)/K se acerca a K/K o 1, y el lado derecho de la ecuación se reduce a r max N, lo que significa que la población está creciendo exponencialmente y no está influenciada por la capacidad de carga . Por otro lado, cuando N es grande, (K-N)/K se acercan a cero, lo que significa que el crecimiento poblacional se ralentizará mucho o incluso se detendrá. Así, el crecimiento poblacional se ve muy desacelerado en grandes poblaciones por la capacidad de carga K. Este modelo también permite que la población tenga un crecimiento poblacional negativo, o una disminución poblacional. Esto ocurre cuando el número de individuos en la población supera la capacidad de carga (porque el valor de (K - N)/K es negativo).
Una gráfica de esta ecuación produce una curva en forma de S (Figura\(\PageIndex{1}\)), y es un modelo más realista de crecimiento poblacional que crecimiento exponencial. Hay tres secciones diferentes a una curva en forma de S. Inicialmente, el crecimiento es exponencial porque hay pocos individuos y amplios recursos disponibles. Entonces, a medida que los recursos comienzan a limitarse, la tasa de crecimiento disminuye. Finalmente, el crecimiento se nivela en la capacidad de carga del ambiente, con pocos cambios en el tamaño de la población a lo largo del tiempo.
Papel de la competencia intraespecífica
El modelo logístico asume que cada individuo dentro de una población tendrá igual acceso a los recursos y, por lo tanto, las mismas posibilidades de supervivencia. Para las plantas, la cantidad de agua, luz solar, nutrientes y el espacio para crecer son los recursos importantes, mientras que en los animales, los recursos importantes incluyen alimentos, agua, refugio, espacio de anidación y mates.
En el mundo real, la variación fenotípica entre individuos dentro de una población significa que algunos individuos se adaptarán mejor a su entorno que otros. La competencia resultante entre los miembros de la población de la misma especie por recursos se denomina competencia intraespecífica (intra- = “dentro”; específica = “especie”). La competencia intraespecífica por los recursos puede no afectar a las poblaciones que están muy por debajo de su capacidad de carga; los recursos son abundantes y todos los individuos pueden obtener lo que necesitan. Sin embargo, conforme aumenta el tamaño de la población, esta competencia se intensifica. Además, la acumulación de productos de desecho puede reducir la capacidad de carga de un ambiente.
Ejemplos de Crecimiento Logístico
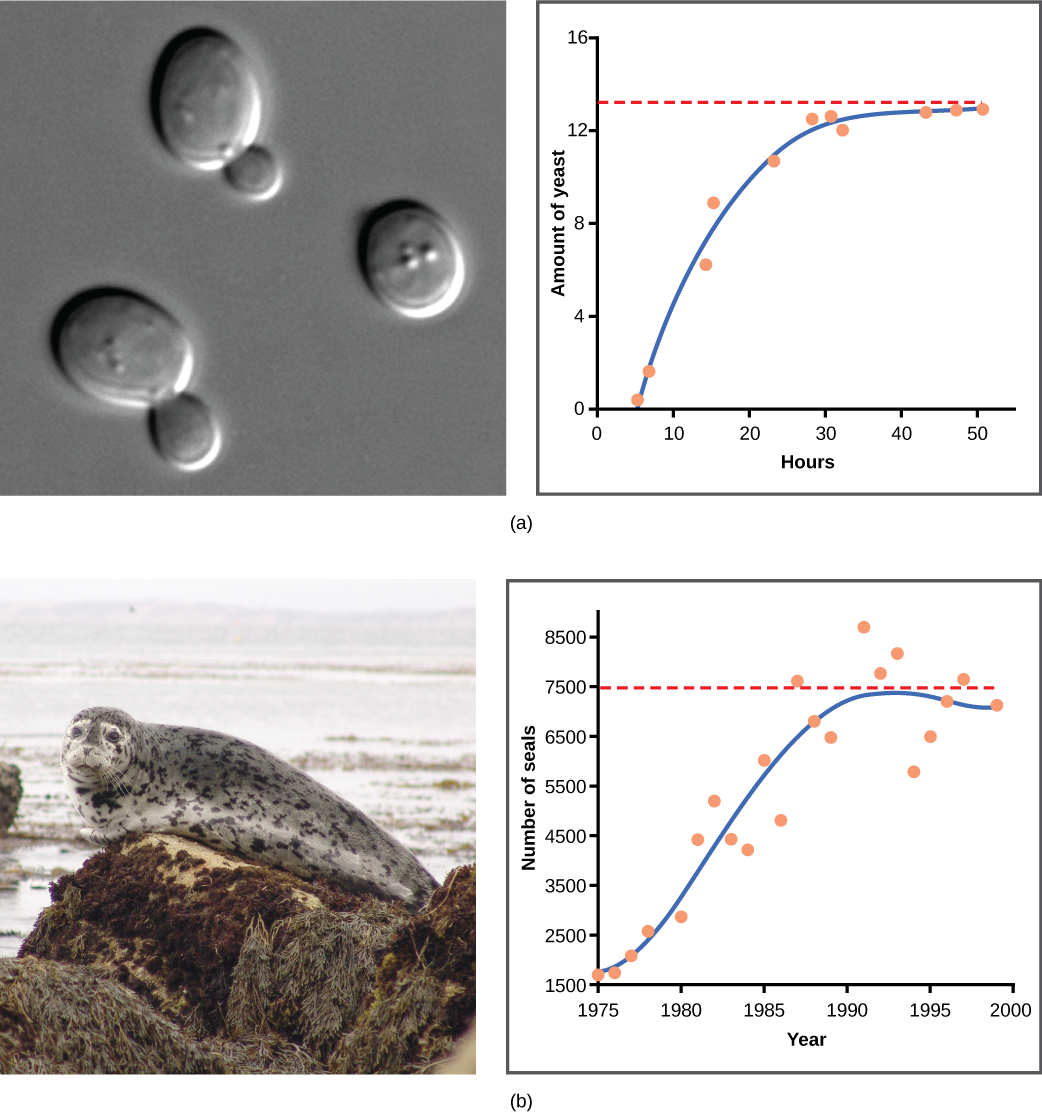
La levadura, un hongo microscópico utilizado para hacer pan y bebidas alcohólicas, exhibe la curva clásica en forma de S cuando se cultiva en un tubo de ensayo (Figura\(\PageIndex{2}\) a). Su crecimiento se nivela a medida que la población agota los nutrientes necesarios para su crecimiento. En el mundo real, sin embargo, hay variaciones a esta curva idealizada. Los ejemplos en poblaciones silvestres incluyen ovejas y focas de puerto (Figura\(\PageIndex{2}\) b). En ambos ejemplos, el tamaño de la población supera la capacidad de carga por cortos periodos de tiempo y luego cae por debajo de la capacidad de carga posteriormente. Esta fluctuación en el tamaño de la población continúa ocurriendo a medida que la población oscila alrededor de su capacidad de carga. Aún así, incluso con esta oscilación, se confirma el modelo logístico.
Resumen
Las poblaciones con recursos ilimitados crecen exponencialmente, con una tasa de crecimiento acelerada. Cuando los recursos se vuelven limitantes, las poblaciones siguen una curva de crecimiento logístico. La población de una especie se nivelará a la capacidad de carga de su entorno.
Referencias
OpenStax, Biología. OpenStax CNX. 26 de junio de 2020. https://cnx.org/contents/GFy_h8cu@10.137:noBcfThl@7/Understanding-Evolution.

